仿生机器鱼尾鳍推进效率的多参数优化研究❋

张开升， 杨明明， 王 强， 张保成

(中国海洋大学工程学院机电工程系, 山东 青岛 266100)

鱼类作为地球上出现最早的脊椎动物，经过数亿年的自然选择，进化出了非凡的水中运动能力，其游动具有推进效率高、机动性强、隐蔽性好、噪声低、对周围环境扰动小等优点[l]。正是鱼类这些运动特点启发机器人学者，通过模仿鱼类的运动方式，不断研制和完善具有鱼类运动特点的仿生机器鱼，以期构建采用高效、高机动游动方式的新型水下机器人系统。国内外学者越来越重视仿生机器鱼的研究与开发，并取得了很多阶段性成果。但是，目前仿生机器鱼的推进效率与自然鱼类仍相差较远[2-3],仅仅对尾鳍单一参数进行优化，无法实现高效推进。哈尔滨工业大学的王冉冉[4]通过基于三坐标系的仿鱼机器人稳态游动速度求解算法，分别研究鱼体的振幅、频率、尾鳍最大击水角度等参数对推进效率的影响，得出最大的推进效率只有33%；中国科学技术大学的陈宏[5]，通过Froude游动效率仿真，得出的最好平均效率为0.58；弗吉尼亚理工学院的A K Kancharala 和M K Philen[6]对尾鳍水动力性能进行了研究，得到的最大推进效率只有45%。这些研究成果相比于自然界中鱼类90%左右的推进效率相去甚远。

本文针对目前仿生机器鱼优化推进效率的研究现状，提出对尾鳍推进进行多参数优化的思路，使各参数相互配合，以接近自然鱼类的真实游动，从而使仿生机器鱼达到较高的推进效率。

1 尾鳍运动参数

尾鳍的运动实质是由多个简单的动作复合而形成的，其中包括平动和转动，而每个简单的动作又可以用不同的参数进行描述。本文将尾鳍的复杂运动分解为以下几个参数[6-7]来进行多目标优化。

1.1 转动频率

尾鳍转动频率ω(Hz)，描述尾鳍绕尾柄转动的快慢。O点为尾柄，转动频率的定义如图1所示。

图1 转动频率示意图

1.2 摆动幅值

尾鳍的摆动幅值H(m)，描述尾鳍随尾柄往复摆动的最大距离。

1.3 最大击水角度αmax

尾鳍的击水角度α(Deg)，为尾鳍中心线与尾柄轨迹切线间的夹角，如图2所示。其中最大击水角度αmax是尾鳍摆动幅值为0时，尾鳍中心线和尾柄轨迹切线间的夹角。击水角度对推进力和侧向力的方向变化起着重要的作用，在不同的游速下，最大击水角度各不相同。由于尾鳍在运动过程中击水角度随时发生变化，因此本文用最大击水角度αmax描述其对推进效率的影响。

图2 尾鳍最大击水角度示意图

1.4 摆动周期

尾鳍的摆动周期T(s)，描述尾鳍随尾柄由初始位置经过一次往复摆动恢复到原位置所用的时间。尾鳍的摆动是一个复合运动，即尾鳍转动与y轴方向尾柄平动的合成运动，因而其摆动周期与转动周期不同，如图3所示。

图3 尾鳍摆动示意图

2 以推进效率为目标的多参数优化设计

2.1目标函数

推进效率是仿生机器鱼研究的重要指标，它是衡量仿生机器鱼推进性能的关键参数，因此，本文研究仿生机器鱼在巡游状态下的推进效率，以此建立目标函数，在前人研究的基础上，提出一种新的优化方法。

鱼类在游动过程中，其有用功是由尾鳍产生的推进力提供的，而无用功则是由侧向力产生的，因此其推进效率计算公式可以定义为：

(1)

式中：WT为推进力作功；WF为侧向力作功。

根据前人成果，可以计算尾鳍上的升力和阻力，其计算公式如下：

(2)

式中：ρ：流体密度；VC：尾鳍速度；CL：升力系数；CD：阻力系数；S：尾鳍面积 。其中，VC是3个速度的合成，包括尾鳍转动速度V1，尾柄平动速度V2和鱼体前进速度u，即VC=V1+V1+u。

则尾鳍在x(鱼体前进方向)和y(垂直于鱼体前进方向)方向的受力为：

(3)

其中：Vy为尾鳍速度在y方向的分量；Vx为尾鳍速度在x方向的分量，其表示如图4所示。

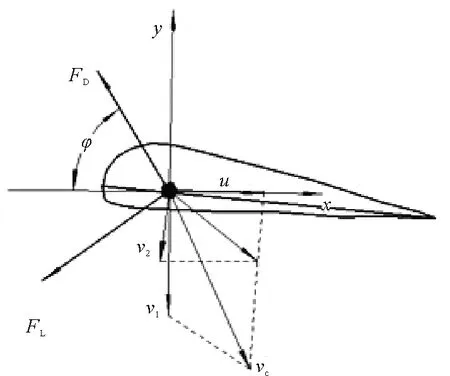
图4 φ角示意图

则尾鳍瞬时产生的有用功率和侧向功率是：

(4)

从而得到运动周期内的平均效率为：

(5)

文中关于尾鳍的参数数据来源于作者所在科研团队的前期研究成果[9]，其中，尾鳍面积S=5×10-3m2，尾鳍的弦长：l=45 mm。

2.2 约束条件

本文依据目前单一优化推进效率的参数所得到的结果，再结合本文具体的模型，给出了适合本文的参数变化范围。

2.2.1 转动频率 目前对仿生机器鱼推进力及推进速度的研究中，选择的摆动频率一般在5 Hz以下，本文将转动频率的取值范围设为ω∈[0,10]。

2.2.2 摆动幅值 鱼类在游动过程中，其摆动幅值要受到体长(L)的限制，摆动幅值一般不会超过体长的20%，本文所用模型体长为L=0.69 m，因此摆动幅值的范围是H∈[0，0.2L]。

2.2.3 摆动周期 由于本文模型的摆动幅值和优化时所选游速的限制，因此摆动周期的取值范围是T∈[0，20 s]。

2.3 优化求解及结果分析

2.3.1 优化求解 本文采用遗传算法进行目标函数的优化。

2.3.1.1 编码 由于二进制编码方式简单，便于实现交叉、变异等遗传操作，本文采用24位的二进制编码方案对参数进行编码。

2.3.1.2 产生初始种群 本文选择初始种群的个体数目为200个。

2.3.1.3 计算适应度 本文所优化的目标函数为效率的最大值，所以直接引用目标函数作为适应度函数。

2.3.1.4 遗传操作 本文采用锦标赛选择法；交叉操作采用二进制单点交叉，交叉率为0.9；变异操作采用二进制单位变异，变异率是0.1。

2.3.1.5 收敛条件 本文的终止进化代数设定为80代。

2.3.2 优化结果及分析 鱼类稳态游动时游速通常不高，且目前对仿生机器鱼进行效率优化时游速的取值也在1 m/s以下，因此本文分别取游速为0.2L、0.4L、0.6L、0.8L、1L、1.2Lm/s进行参数优化，得到在某一特定游速下的最佳参数取值。本文将所得幅值H换算成体长的倍数，以便得到幅值与体长的关系。得到的参数优化结果如表1所示。

据此，其推进效率与巡游速度的关系如图5所示。

从图5可以看出尾鳍推进效率和游速之间的关系，游速在0.2L～0.6Lm/s之间时，推进效率随游速的增加而增大，其原因在于随着尾鳍摆动速度的增加，推进力增加的速度大于侧向力；当稳态游动速度在0.6Lm/s时推进效率达到最大，这是因为尾鳍推进力增加的速度和侧向力相同；当游速大于0.6Lm/s后，推进效率随着游速的继续增大而逐渐下降，这是因为尾鳍的摆动幅值和频率在不断增大，侧向力增加的速度超过推进力，消耗在水中的无用功也在持续增加。因此本文的研究对象游速在0.6Lm/s时推进效率最佳。

表1 参数优化结果

图5 效率变化趋势图

转动频率趋势和摆动幅值、周期趋势分别如图6、7所示，可以看出随着游速的增大，尾鳍转动频率和摆动幅值都在单调递增，角频率是随着游速的增大，增大的幅度在加快，而幅值增加的幅度在减缓，这说明增大转动频率和摆动幅值都能使游速加快，但由于体长的原因幅值不能无限增大，如果需要加速只能通过增大尾鳍转动频率的来达到目的。尾鳍的摆动周期变化趋势如图7所示，摆动周期随着游速的增大而单调减小，是因为摆动频率在增大，因此相应的周期也会减小。

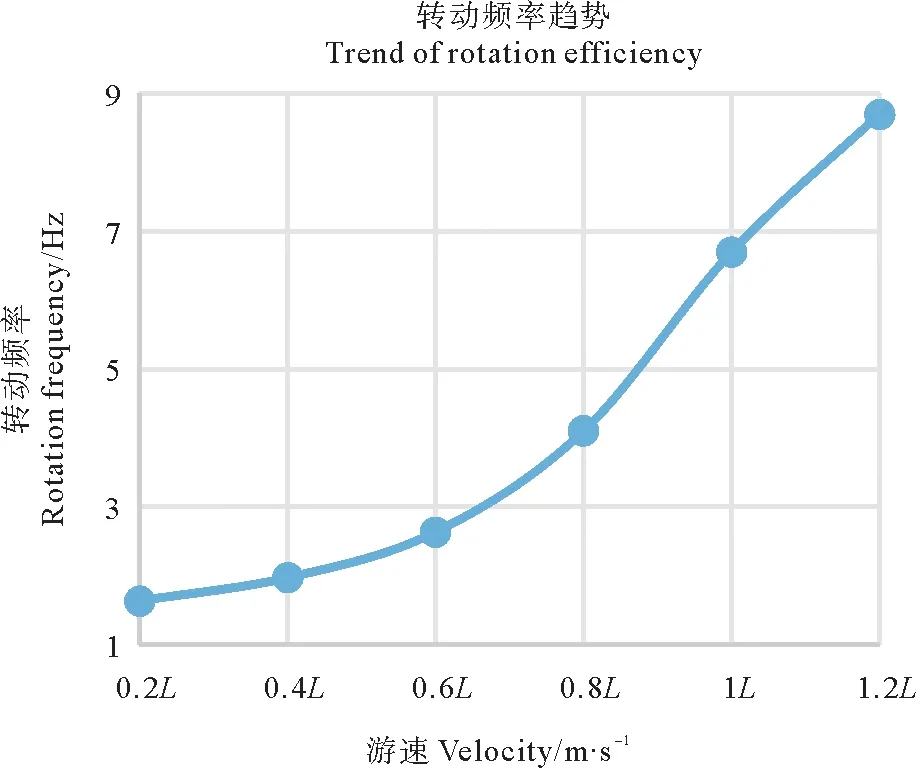
图6 转动频率变化趋势图

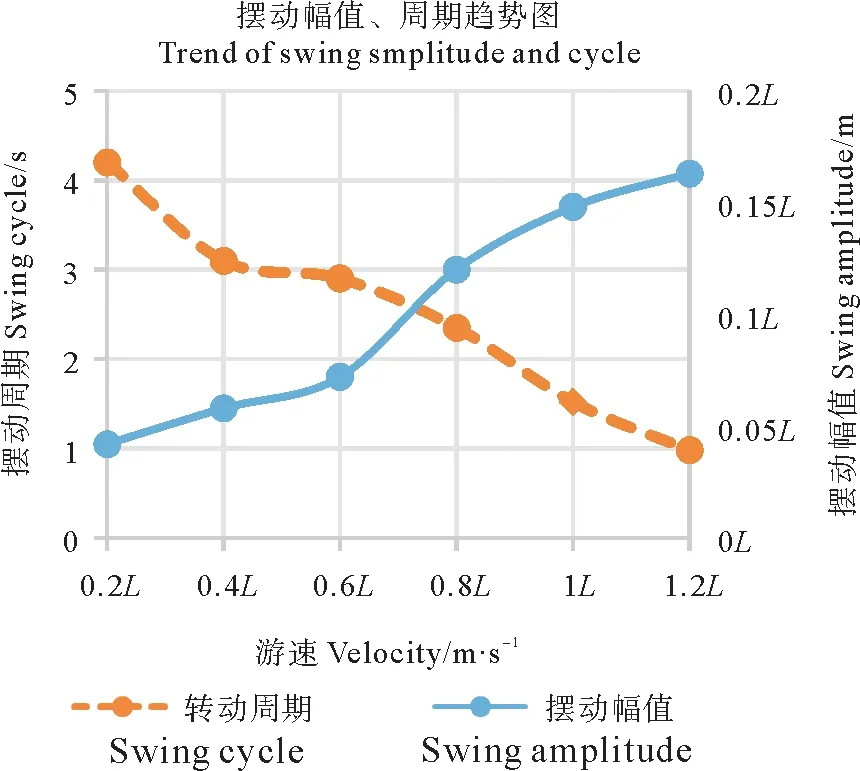
图7 摆动幅值、周期变化趋势图

尾鳍的最大击水角度变化趋势如图8所示，可知其随着游速的增加而单调递增，这说明当机器鱼需要比较大的推进力时，尾鳍就会需要一个比较大的击水角度来产生足够的推进力，这个数据也吻合王冉冉[4]的研究成果。

3 仿真验证

本文使用仿真软件FLUENT进行仿真，并采用了动网格技术。仿真尾鳍在各游速下实际的推进效率，并与优化得到的推进效率相比较，来验证上述算法是否正确。

图9为本文采用的物理模型，图10为本文仿真验证所用的网格。

图8 最大击水角度变化趋势图

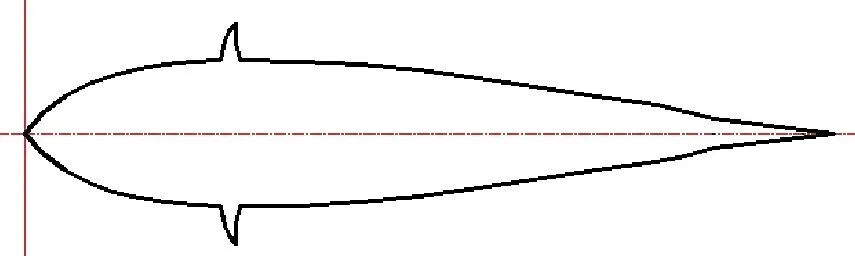
图9 仿生机器鱼的物理模型

图10 仿生用网格

动网格仿真所需数据是各稳态游速下进行效率优化所计算出的结果，将这些数据加入到UDF中，就可以进行仿真。图11为游速为0.6Lm/s时推进效率的仿真结果。

图11 游速0.6Lm/s时仿真结果图

图中，(1 0 0)代表游动方向(x方向)上0.5个周期内产生的平均推进力FT，(0 1 0)代表水平面内游动垂直方向(y方向)上0.5个周期内产生的平均侧向力FF。其推进效率为：

(6)

采用同样的方法可得出其他游速时的效率，结果如表2所示。

表2 仿真效率

图12、13分别为游速0.6L和1.2Lm/s时的压力云图，可以看出游速为0.6Lm/s时尾鳍两侧受到的压差大于游速为1.2Lm/s时的压差，这说明游速0.6Lm/s时，尾鳍所受到的由压差产生的推进力较大，这也从另一方面说明了为什么游速0.6Lm/s时的推进效率高于1.2Lm/s。

将数值计算的效率和仿真结果进行对比，如图14所示，从图中可以看出2种方法得到的结果变化趋势是一致的，且数值接近，这说明本文所提出的数值计算方法是正确的。仿真所得效率值比数值计算结果稍低，这是因为仿真时流体粘性所产生的影响所致。

图12 游速0.6Lm/s时压力云图

图13 游速1.2Lm/s时压力云图

图14 仿真结果与数值结算结果效率对比图

陈宏在“仿生机器鱼巡游和机动的运动机理研究”[5]中，得到的推进效率为0.58；陈斐[10]仿真了尾鳍的摆动幅值和摆动频率等单一参数变化对推进效率的影响，得到的最高仿真推进效率是0.62。而本文的最高仿真推进效率达到了0.643，相较于其他的研究成果有了一定的提高，这主要是因为本文将尾鳍的转动频率、摆动幅值、最大击水角度和摆动周期这4个参数进行了综合优化，在游动过程中各参数之间密切协同，使尾鳍处于最佳工作姿态，从而提高了推进效率。

4 结语

本文根据仿生学的研究定义了尾鳍的4个游动参数，依据细长体理论建立了评价推进效率的数学公式，并进行了以推进效率为目标函数的多参数优化设计，采用遗传算法对目标函数进行了多参数优化，通过FLUENT软件对尾鳍的推进效率进行仿真，并将仿真结果与优化结果进行对比。

本研究得到的尾鳍最高仿真推进效率为0.643，最高数值计算推进效率为65.7%，通过对比目前的研究成果可以发现，尾鳍的多参数优化产生的效率高于单参数优化的效率，且存在不小的差距。因此，本研究所提出的尾鳍多参数优化方法是正确的。本研究针对研究目标得出的最佳巡航速度是0.6Lm/s，但是不同的游速都可以得出一组最佳的配合参数，这就为以后仿生机器鱼的控制开辟了一种新的思路，在特定游速下首先优化出一组参数，通过这些参数的密切配合，达到在这种特定游速下效率最高的效果。