基于抽样分布理论的P-Ⅲ型分布均值的不确定性分析

刘可新，胡宇丰，李 匡，刘 鹏，梁犁丽

（1.中国水利水电科学研究院 北京中水科水电科技开发有限公司，北京 100038；2.河南黄河水文勘测设计院，河南 郑州 450000）

1 研究背景

P-Ⅲ型分布广泛应用于我国水文频率计算中［1］，在推求设计暴雨、设计洪水等方面发挥着重要作用。水文过程受气候、地形和下垫面条件等因素影响，存在诸多不确定性规律［2］，如频率计算时往往存在线型选择、参数估计的不确定性等。近些年来，国内外学者围绕水文不确定性进行了大量研究工作［3-6］，并取得了较好的效果，其中基于贝叶斯理论的研究最具代表性，早在1975年，Wood等［7］就应用贝叶斯理论对统计参数不确定性做了分析，近年来，围绕贝叶斯理论在水文方面的应用，我国学者也取得了大量研究成果，刘攀等［8］将贝叶斯理论应用于水文频率的线型选择，结果表明线型的后验概率越大则拟合越好；梁忠民等［9］应用贝叶斯理论进行参数估计，并介绍了贝叶斯理论在水文不确定性方面的研究进展［10］。诸多学者研究表明，贝叶斯理论应用于水文不确定性分析具有较好的效果［11-14］，贝叶斯理论体系较完备，应用于频率计算参数不确定性分析效果较好，贝叶斯理论与经典统计学理论有所不同，其特点是认为不确定性既来自于参数的随机性，也来自于样本的随机性，应用贝叶斯理论分析参数不确定性需对其先验分布做出假设，这将产生较大的主观性。为尽量避免主观性，本文将应用经典统计学理论分析P-Ⅲ型分布参数的不确定性，经典统计学理论认为分布参数应看作常数处理，是确定性的，通常所说的参数不确定性可理解为参数估计量的不确定性，这种不确定性往往是由于以有限的、离散的且存在不确定性的样本去近似总体分布特征（如均值）而产生的，具体又可表述为两方面，一是样本总是有限的、离散的，而总体是无限的、连续的，以有限描述无限、离散描述连续必然存在一些不确定性；二是样本本身存在不确定性，如洪水过程受复杂条件影响而产生不确定性。

鉴于贝叶斯理论分析参数不确定性存在主观因素，本文从经典统计学理论出发，提出基于抽样分布理论的P-Ⅲ型分布均值的不确定性分析方法，在总体分布的离势系数和偏态系数已知情况下，应用经典统计学理论分析均值的不确定性。首先推导样本均值的分布函数，而后构造辅助随机变量并推导其分布函数，最后应用辅助随机变量分析总体均值的不确定性。

2 方法介绍

我国水文系列频率分析普遍采用P-Ⅲ型分布，为更好分析其参数不确定性，提出了基于抽样分布理论的P-Ⅲ型分布均值的不确定性分析方法，该方法是指当随机变量服从P-Ⅲ型分布时，采用抽样分布理论分析其总体均值的不确定性，重点是研究总体均值的置信区间，分析该置信区间与样本均值、离势系数和偏态系数的关系，主要包括以下推导过程和实现步骤。首先阐述抽样分布的概念，推导P-Ⅲ型分布样本均值的分布函数，然后构造辅助随机变量，该随机变量自身含有总体均值，但分布函数与总体均值无关，最后应用辅助随机变量，结合上、下概率分位点得到总体均值的置信区间。

2.1 P-Ⅲ型分布样本均值分布P-Ⅲ型分布的样本均值是指服从P-Ⅲ型分布的随机变量样本均值，简称为P-Ⅲ型分布的样本均值。样本均值的分布属于抽样分布的范畴，所谓抽样分布是指在总体分布已知的情况下，由样本系列经连续函数构造而成的各统计量的分布，如样本均值的分布、样本方差的分布等［15］。我国水文系列大都服从P-Ⅲ型分布，本文将基于该分布推导样本均值的概率密度函数。P-Ⅲ型分布的概率密度函数如下式：

式中，a0、α 、 β 分别为P-Ⅲ型分布的位置、形状和尺度参数。

为便于推导，引入特征函数概念，设随机变量X的概率密度函数为f (x) ，则有：

式（2）为随机变量X的特征函数，其中t为实数，i为虚数单位。

由以上定义，对应于P-Ⅲ型分布的特征函数为：

特征函数具有以下性质：

（1）性质1。分布函数与特征函数是一一对应关系；

（2）性质2。设X，Y为两随机变量，且Y=cX+d（c、d为实常数），则Y的特征函数为：

（3）性质3。设X，Y为二相互独立的随机变量，且Z=X+Y，则：

根据以上性质推导样本均值的特征函数。设随机变量X 服从P-Ⅲ型分布，特征函数如式（3），X1，X2，…，Xn为总体的样本，则它们均相互独立，样本均值为根据性质2 和性质3有的特征函数为：

比较式（6）与式（3）的形式，根据特征函数的性质1 可知仍然服从P-Ⅲ型分布，令α′=nα ， β′=nβ ，则其概率密度函数为：

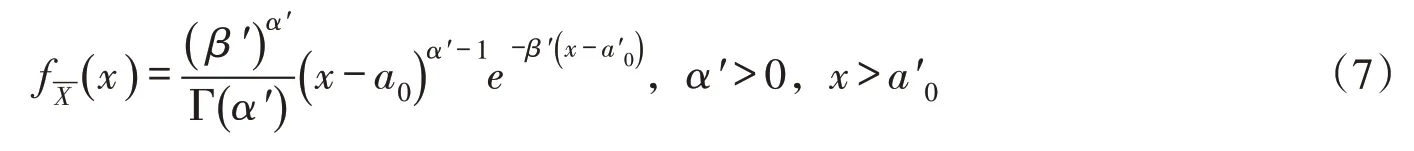
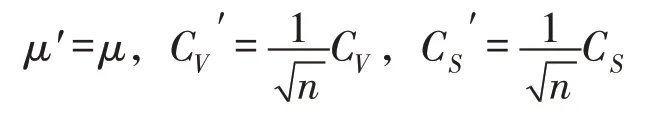
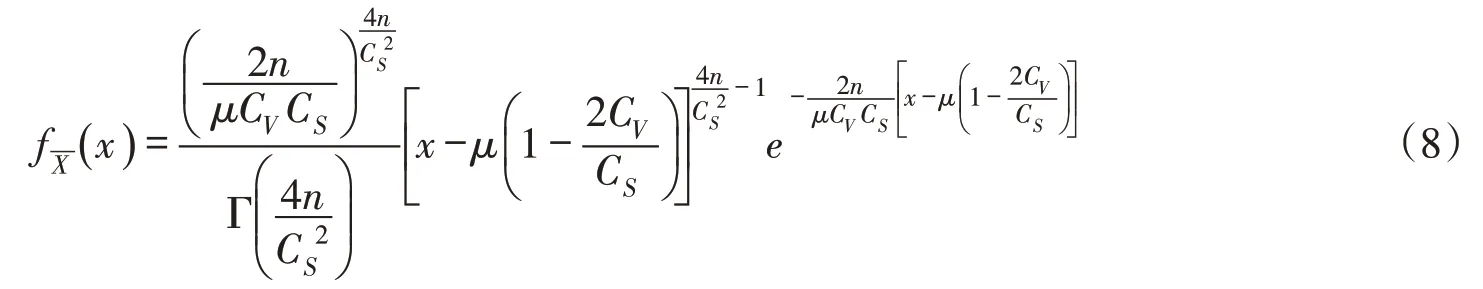
2.2 辅助随机变量及μ 的不确定性分析令称为辅助随机变量，其分布函数为FY( y )，则有：

令Y的概率密度函数为fY( y )，则有：

整理得：

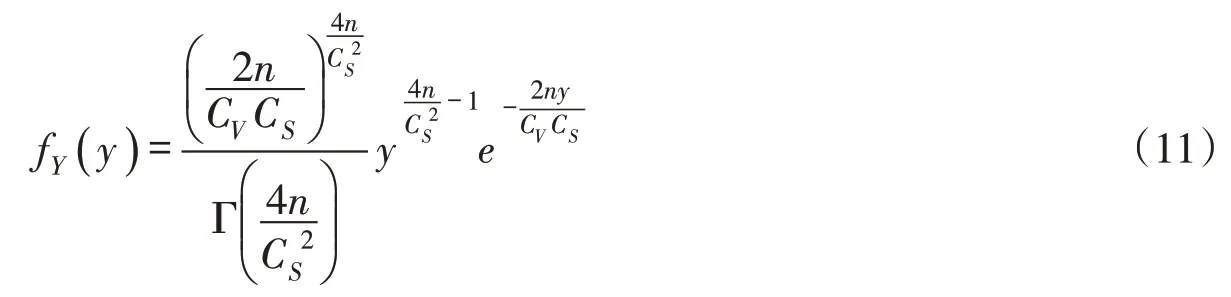
由式（11）可知，Y 服从P-Ⅲ型分布，且概率密度仅与X 的CV和CS有关，与μ 无关，其均值、离势系数和偏态系数分别为：

当X 的CV和CS为已知时，可利用Y 的分布函数分析X 均值( μ )的不确定性，包括μ 的置信区间、 μ 处于某一有限区间的概率、 μ 大于或小于某特定值的概率等问题，其中获得μ 的置信区间是水文上经常关心的问题，因此本文对μ 的置信区间做如下推导。

给定置信度1-a，则有：

具体步骤如下：

（1）获取水文系列总体X的离势系数CV和偏态系数CS，可移用已有参数或通过矩法、极大似然法等方法估算之；计算样本均值；

（4）对应于置信度1-a的μ 的置信区间如式（13）所示。

μ 的不确定性分析包括但不限于获取置信区间，置信区间是本文关注的重点，它可进一步应用于对设计值的不确定性分析，转步骤（5）。

2.3 μ 的置信区间与参数的关系μ 的置信区间与样本均值、总体的离势系数和偏态系数有关，下面在理论上对其做定性分析。

式（13）可化简为：

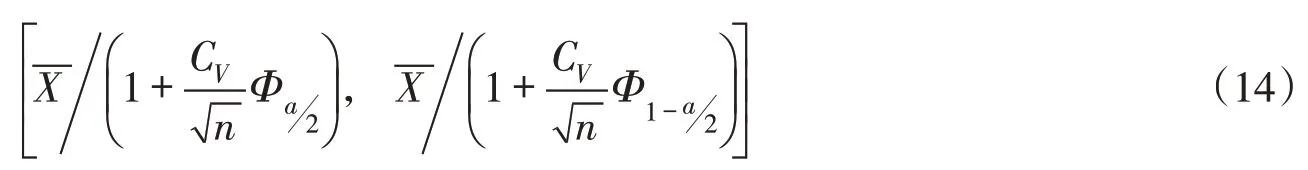
3 实际流域应用与分析

上犹江属江西省赣江水系章江的一条支流，发源于湖南省汝城县和江西省崇义县、上犹县至南康县的三江口汇入章江，全长200 km。干流上修建有上犹江水库，坝址以上控制面积为2750 km2，上犹江水库流域属于亚热带湿润季风气候，冬夏季风盛行，冬季盛行极地大陆性气团，气候干冷而少雨雪；夏季盛行来自热带的海洋气流，气候湿润而多雨，多年平均降水量为1675.5 mm，分配极不均匀，4—9 月占全年70.3%，暴雨虽一年四季都会出现，但主要出现在春夏两季，暴雨出现的机率占全年的80%以上，而冬季（12、1、2月）暴雨日数仅占全年的1%，多年平均流量为79.5 m3/s。

本文将该方法应用于上犹江流域，分别采用矩法和适线法以1997—2016年20年的水文资料推求洪峰系列的样本均值、离势系数和偏态系数，并将样本的离势系数和偏态系数近似代替总体的离势系数和偏态系数，给定置信度为90%，计算洪峰系列均值的置信区间，并推求对应于上述置信区间的十年一遇、百年一遇和千年一遇的设计洪峰。方法参数及设计洪峰结果如表1和表2。

表1 洪峰系列统计参数

表2 不同频率设计洪峰

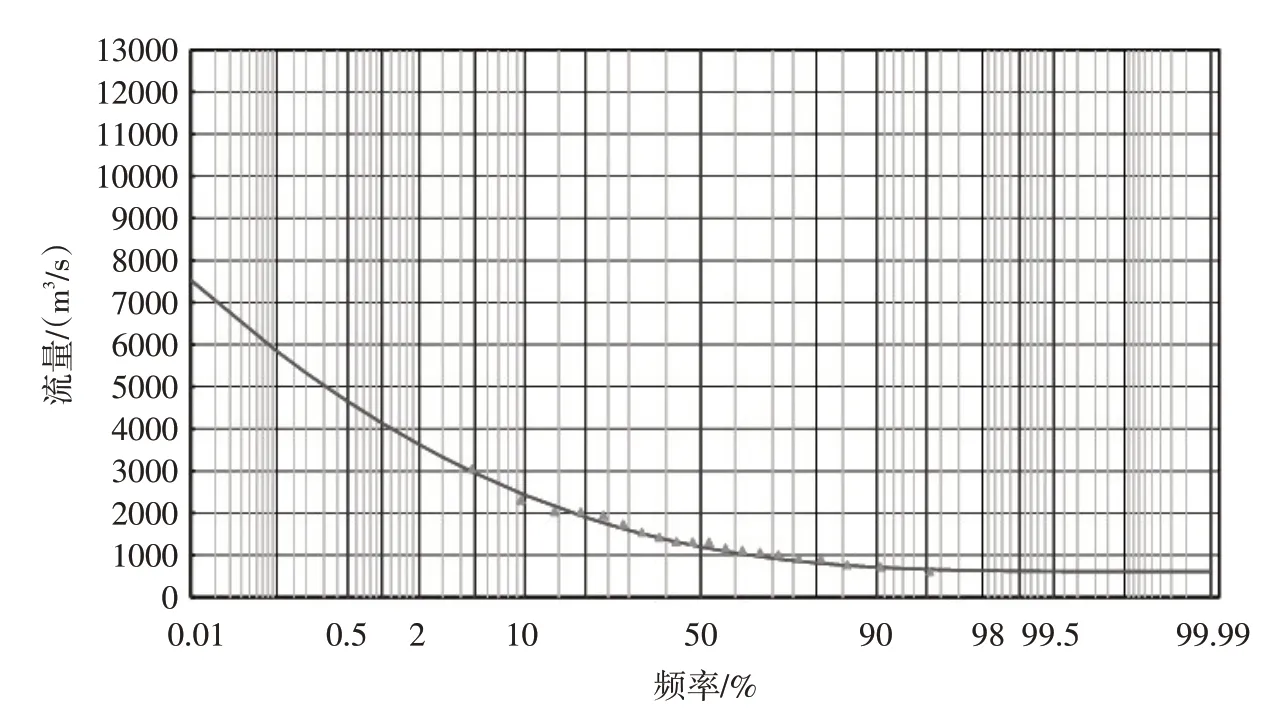
图1 适线法结果

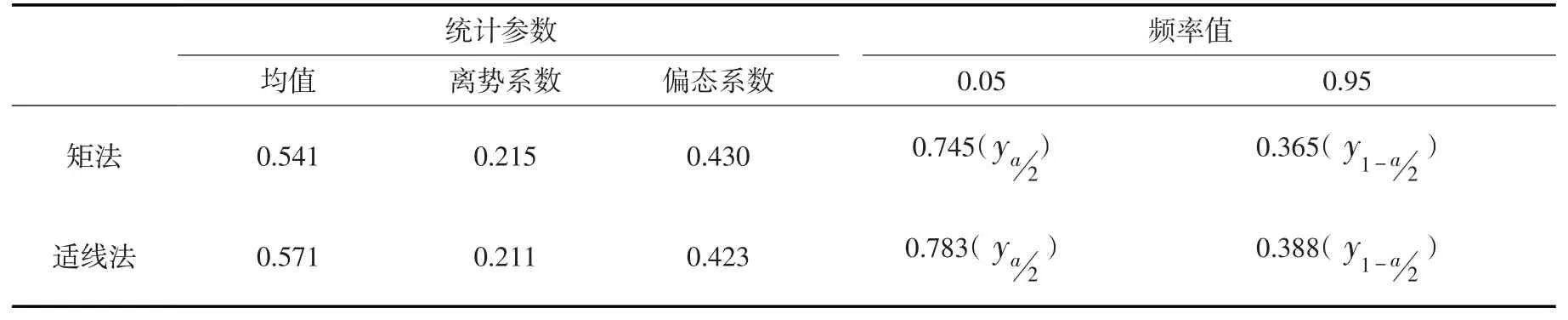
表3 辅助随机变量Y的分布参数及上下概率分位点

表4 90%置信度洪峰均值及设计洪峰置信区间

以样本离势系数和偏态系数作为总体离势系数和偏态系数，计算随机变量Y的分布参数，并计算置信度为90%的上下概率分位点如表3。按式（13）得到洪峰均值的置信区间，进而计算各频率下的洪峰流量及置信区间如表4。

以上结果显示新方法应用于总体均值和设计值的不确定性分析是可行的，从表4结果看，90%置信度下，矩法和适线法的区间估计结果略有不同，矩法洪峰均值的置信区间为［1180，1724］，其区间宽度略小于适线法［1172，1738］；洪峰设计值的区间估计也有所差异，各频率下矩法的结果整体偏小于适线法，但仍具有较大的重合部分，千年一遇、百年一遇和十年一遇区间重合率（重合部分/总区间宽度）分别为0.876、0.882和0.907，表明两种方法的分析结果具有一定的一致性，且一致性随预见期的减小而增大。

虽然矩法和适线法的分析结果具有一定的一致性，但其差异也较显著，主要是离势系数和偏态系数的估计值不同所致，下面通过实例分析离势系数和偏态系数与总体均值置信区间的关系。

表1中，适线法的样本均值取计算结果1420 m3/s；离势系数经调整后取0.54较合适；根据上犹江流域的水文特点，偏态系数一般取离势系数的3.5倍［16］为1.89，适线结果如图1。

取适线法的相关参数，仅对总体离势系数做调整，总体均值的置信区间如表5，其宽度变化趋势如图2。

表5 不同离势系数对应总体均值的置信区间

图2 离势系数与总体均值置信区间的关系

表6 不同偏态系数对应总体均值的置信区间

表5结果显示，离势系数对总体均值的置信区间具有较大影响，不同的离势系数对应的区间宽度具有较大差异。图2显示，当其他条件一定时，总体均值的置信区间下限随离势系数的增大而减小，上限则恰好相反，因此，正如图中所示置信区间宽度将随离势系数的增大而增大，且较小的置信区间包含于较大者之中，这与2.3节理论分析结果是一致的。

同理可进一步分析偏态系数的影响，结果如表6和图3。

综上，离势系数与偏态系数对总体均值不确定性的分析结果具有一定影响，但其程度及影响效果不同，离势系数的影响效果较为显著，且随着离势系数增大置信区间宽度也增大；而偏态系数恰好相反，其影响远不如离势系数显著，且影响效果也与离势系数相反，表现为随偏态系数的增大，置信区间宽度略有减小。

图3 偏态系数与总体均值置信区间的关系

4 结论与展望

4.1 结论本文首先阐述了对分布参数不确定性的理解，认为通常所说的参数不确定性可表述为参数估计量的不确定性，进而提出了基于抽样分布理论的P-Ⅲ型分布均值的不确定性分析方法，在分析过程中首先应用抽样分布理论，推导了P-Ⅲ型分布样本均值的分布函数，构造了辅助随机变量并推导了其分布，最终在总体离势系数、偏态系数已知情况下推导了均值的置信区间并应用于上犹江流域。经理论推导与实际应用，得到以下几点结论：（1）P-Ⅲ型分布的样本均值服从P-Ⅲ型分布，如果总体分布的均值、离均系数、偏态系数为μ 、CV、CS，则样本均值的均值、离均系数、偏态系数为（2）如果水文系列X服从P-Ⅲ型分布（参数为μ，CV，CS），则辅助随机变量服从参数为的P-Ⅲ型分布，可见其分布参数仅与CV和CS有关，而与μ 无关；（3）P-Ⅲ型分布已知总体的离均系数、偏态系数时，应用抽样分布理论可分析总体均值的置信区间，并且可避免主观因素影响；（4）实际流域应用效果表明应用新方法分析设计洪峰的不确定性是可行的，其分析结果受总体离势系数的影响较大，而受偏态系数影响较小。

4.2 展望本文提出的新方法可分析P-Ⅲ型分布均值的不确定性，但前提是总体的离势系数和偏态系数已知，该条件较为苛刻，今后将进一步加强理论研究，以期放宽应用条件，主要有以下几点展望：（1）该方法无需先验分布假设，很大程度上避免了主观因素影响，在今后研究中应把放宽应用条件作为重点，并通过理论推导逐步扩展到对CV和CS的不确定性分析；（2）t分布和χ2分布是由正态分布衍生而来，可用以辅助正态分布均值和方差的区间估计，参考上述关系，有望推导相应于P-Ⅲ型分布的衍生分布，在不附加任何条件的情况下，用以分析P-Ⅲ型分布各参数的不确定性。