钢筋混凝土空心高墩振动特性分析

潘桂超，田石柱, 2

(1.苏州科技大学土木工程学院，江苏苏州215011; 2.江苏省结构工程重点实验室，江苏苏州215011)

0 引言

近些年来，我国桥梁工程发展迅速，在地势险峻的山区，在城市高速公路连接之间，以及在广阔的海面上，建成了一批结构新颖、技术复杂、设计和施工难度大、科技含量高的高墩桥梁。为实现低碳经济，节约高墩的成本，目前大部分工程都采用空心桥墩[1]254。相同尺寸的空心桥墩与实心桥墩相比，大大减少了材料用量，具有较高的性价比[2]。空心高墩的振动情况与实体高墩差异较大，对于钢筋混凝土空心高墩的振动特性的研究，具有重大实际意义。

目前国内外众多学者对高墩桥梁的抗震性能进行了许多研究，比如： Mander[3]分别以矩形和圆形截面的空心桥墩为研究对象，通过拟静力实验对其抗震性能进行研究。Zahn[4]为了研究钢筋混土空心桥墩的强度和延性，进行了大量的恒轴向力下的桥墩拟静力实验。杜修力、Lehman等[1，5]对12个钢筋混凝土空心桥墩进行了低周反复荷载作用下的抗震实验研究。众多研究表明，空心桥墩具有良好的抗震能力[6]。

本文从理论公式推导入手，引入壁厚系数β，推导出模态频率fn与壁厚系数β的函数关系，并对函数进行研究，探索壁厚对钢筋混凝土空心桥墩振动特性影响的规律。通过Abaqus软件的Lanczos算法对不同横截面形式、不同壁厚系数β的钢筋混凝土空心高墩实体模型、线单元模型进行模态分析，提取前三阶自振频率与理论计算值对比分析，验证其振动特性变化规律的准确性。

1 模态分析方法

模态分析是研究结构动力特性一种常用方法，在工程振动领域中应用广泛。模态是指工程结构的固有振动特性，每一个模态都有特定的固有频率、阻尼比和模态振型[7—8]。分析这些模态参数的过程称为模态分析。

对于不考虑阻尼影响下的一般结构而言，其基本运动方程[9]可表示为

(1)

式中：x为位移向量，[M]、[K]分别为结构固有的质量矩阵和刚度矩阵。

钢筋混凝土空心墩可以近似简化为一个具有相当弹性模量的均匀等效的弹性结构进行计算分析。相当弹性模量[10]为

(2)

式中：ES、IS分别为钢筋对中性轴的弹性模量、惯性矩；EC、IC分别为混凝土对原点的弹性模量、惯性矩；I为均匀材料对中性轴的惯性矩。

本文研究的钢筋混凝土空心高墩结构是一个高柔的结构，其边界条件为一端固结，一端自由。若只考虑其水平方向的位移和截面转角变形，忽略剪切变形的影响，则钢筋混凝土空心高墩的运动方程可以简化成

(3)

根据悬臂梁的边界条件(固接端x=0；自由端x=L，L为墩高)，求得悬臂梁的自振圆频率：

(4)

式中：a1L=1.875；a2L=4.694；a3L=7.855；

基于前面的均匀等效的假定，将钢筋混凝土桥墩视为一个具有相当弹性模量的均匀等效的弹性结构，由式(4)知anL是常数，若桥墩的高度、材料再确定，则E、L以及密度ρ也是常数，式(4)可简化为

(5)

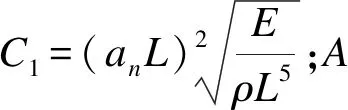
以圆形为例，令壁厚系数

式中：D为大圆直径；d为小圆直径；B为壁厚。

将相关数据代入式(5)，化简得

(6)

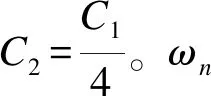
(7)

以矩形为例，本文只考虑提取顺桥向(即X方向)前三阶自振频率。

令壁厚系数

式中：b、h分别为大矩形的底长、高；b′、h′分别为小矩形的底长、高；Bb为矩形底长方向(即X方向)的壁厚；Bh为矩形高方向的壁厚。

将相关数据代入式(7)，并化简得

(8)

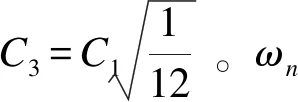
(9)

当b=h时，矩形为正方形，式(8)、(9)仍成立。

自振频率

(10)

综上所述：当β<1时，圆形、矩形两种截面形式的空心高墩的自振频率fn也是关于壁厚系数β的单调递减函数；当β=1时，fn=0。

2 Abaqus有限元模型

2.1 Abaqus有限元模型设计

本文利用Abaqus软件建立了24组不同截面形式、不同壁厚系数β的钢筋混凝土空心高墩实体单元模型，并加以相同的边界条件(一端固结、一端自由)进行模态分析。模型截面类型分别为圆形(R=2 m)、正方形(4 m×4 m)、长方形(3 m×5 m)。各截面有限元模型桥墩特性详细数据如下：墩高为50 m；配筋率为1.5%；配箍率为1.20%；壁厚系数β分别为0.2、0.25、0.35、0.4、0.45、0.6、0.8、1。各截面形式空心高墩配筋如图1所示。

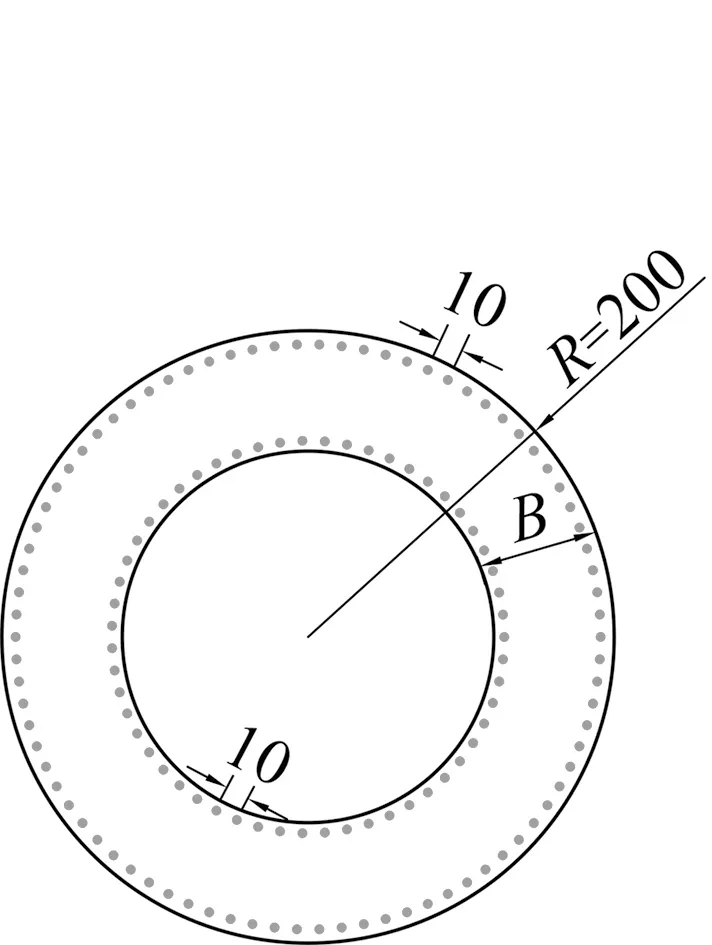
(a)圆形

(b)正方形

(c)长方形

(d)墩身

图1 各截面形式空心墩配筋图(单位：cm)

2.2 材料属性的设置

空心桥墩的质量和刚度会影响其自振频率和振型。本文中所有的空心高墩均采用C40混凝土和SOLID65单元，混凝土的材料参数为密度2.5×103kg·m-3、弹性模量3.25×1010Pa、泊松比0.2。钢筋材料属性见表1。

表1 钢筋材料属性

2.3 实体单元模型频率计算

在模态分析中，因振动被假定为自由振动，所以只有边界条件起作用，其他荷载对结构分析结果没有影响。在Abaqus中具体实现较为简单，设置分析步为线性摄动步(liner perturbation)中的频率提取分析步(frequency extraction)。本文这里只提取前三阶顺桥向的自振频率[11—12]。具体数据见表2。

2.4 线单元模型频率计算

由于钢筋混凝土空心高墩是一个长细比较大的结构，如果截面方向上应力影响可以忽略，采用线单元模型将会避免实体模型网格划分过程中发生畸变的问题，并且在计算速度上有较大的提高。本文在实体单元模型的基础上建立对应的线单元模型进行计算分析，具体数据见表3。

表3 线单元模型前三阶自振频率

2.5 理论分析模型频率计算

基于前面假定，将钢筋混凝土空心高墩视作均匀等效的弹性结构，其相当弹性模量E≈3.57×1010Pa。运用公式(4)，计算各截面形式的空心高墩顺桥向的前三阶自振圆频率，换算成自振频率。详细数据见表4。

表4 理论计算模型前三阶自振频率

3 计算结果分析

3.1 实体模型计算结果分析

针对上述不同截面形式钢筋混凝土空心高墩实体结构模型，本文对其前三阶顺桥向自振频率进行研究分析。由表2可见，前三阶自振频率随着壁厚系数β减小而增大。这验证了前面理论推导公式的准确性。另外，研究发现，随着壁厚系数β减小，空心高墩的质量也大幅度减小，并且自振频率f增幅远远比不过质量的降幅，如图2所示。

(a)圆形实体模型

(b)正方形实体模型

(c)长方形实体模型图2 不同截面实体模型自振频率及墩身质量变化

以质量变化差异较大的正方形截面空心高墩模型为例，壁厚系数β从1.0降到0.2时，第一阶频率f1从0.153 Hz增至0.188 Hz，仅增加了0.035 Hz，增幅约为22.8%，但是质量却从2 000 t降到720 t，下降了1 280 t，降幅达到了64%。这在工程设计中有比较大的指导意义，当桥墩的墩高、截面尺寸确定，在满足安全承载力的前提下，可以通过缩减壁厚的方式，大幅度降低混凝土用量，并且保证高墩前几阶主频率变化不大，达到降低成本的目的。

3.2 线单元模型与实体模型的计算结果对比分析

线单元模型是在忽略截面方向的应力、应变影响的前提下，对实体模型的一种简化，以便快速得到结构的主频率。各截面形式空心高墩的线单元模型相对于实体模型的前三阶自振频率误差如表5所示。可以发现绝大部分误差都控制在6%以内，但是有小部分数据误差在14%左右，这小部分数据集中在壁厚系数β为0.8至1之间，再进一步分析表4，发现当壁厚系数β为1.0时，结构的自振频率却增大，不符合自振频率随壁厚系数增大而降低这一变化规律。分析原因，当壁厚系数β在0.8至1之间时，壁厚约占高度的3/50，截面面积甚至达到10 m2至16 m2，截面方向的应力、应变影响无法忽略，所以这2组数据的误差较大。除去壁厚系数β为0.8和1.0这2组不太准确的数据，整体上线单元模型也反映出前三阶自振频率随着壁厚系数β增大而降低这一变化规律。虽然线单元模型在壁厚系数β为0.8和1的2组误差较大，但是相对于薄壁空心高墩而言，采用线单元模型可以快速计算结构的前几阶自振频率，误差也在允许范围内。

3.3 理论计算模型与实体模型的计算结果对比分析

理论计算模型是基于这样的假定：钢筋混凝土空心高墩可以视作一个具有相当弹性模量的均匀等效的弹性结构，并且可以忽略剪切变形，只考虑其水平方向的位移和截面转角变形，其运动为平面弯曲，符合平截面假定。因此，理论计算值与有限元实体模型存在一定的误差(见表6)。

表5 线单元模型前三阶自振频率误差

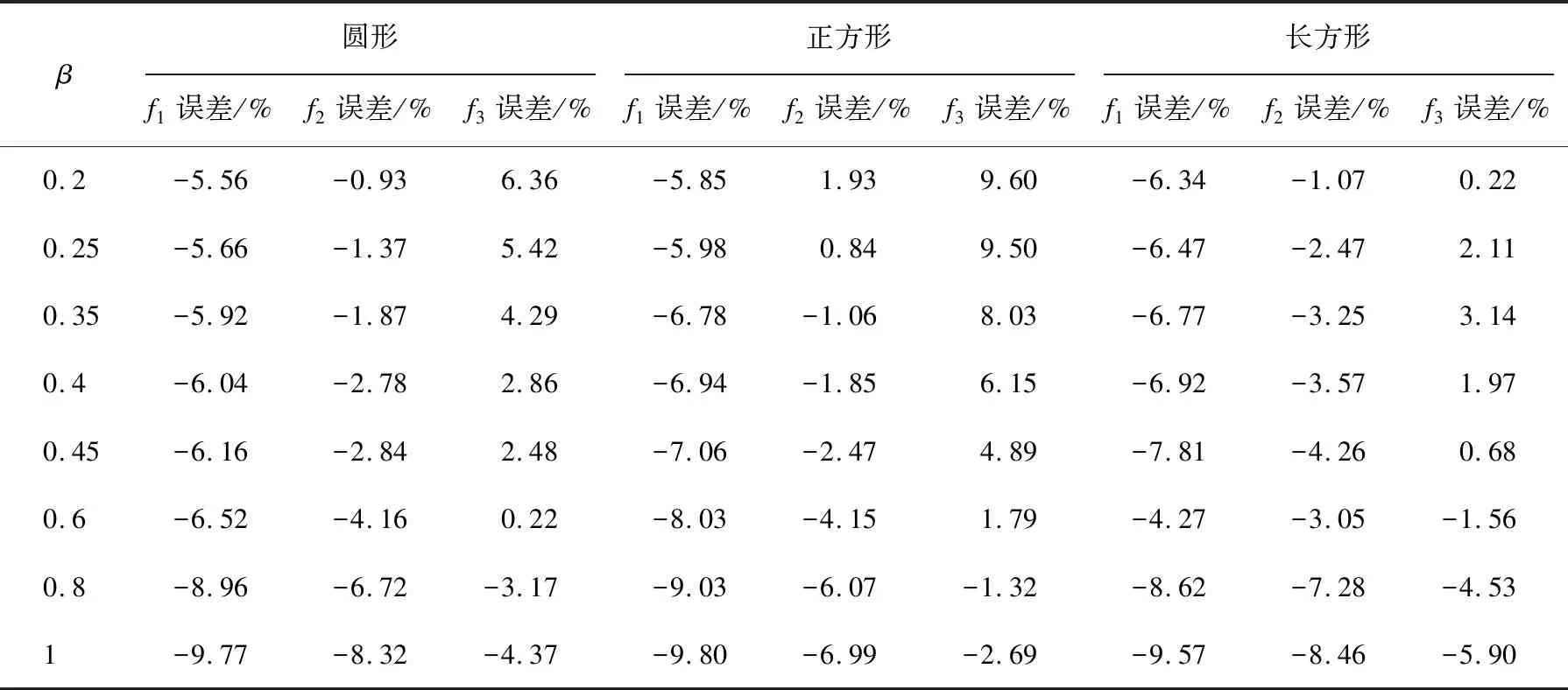
表6 理论计算模型前三阶自振频率误差

表6中数据显示：第一阶频率f1的理论计算值误差均为负值，即有限元实体模型的第一阶频率高于理论计算值。这主要是由于有限元实体模型计算结果是基于Abaqus软件的Lanczos算法。Lanczos算法本质上是向量反迭代法和Rayleigh-Ritz法结合的一种方法[13]，而理论计算模型的计算方法是基于欧拉-伯努利梁理论。相关研究表明：Rayleigh-Ritz法求得悬臂梁的一阶固有频率要比欧拉-伯努利梁理论求得的一阶固有频率偏大，这与本文得到的结果相一致。从误差角度分析，第一阶频率误差最小的是长方形截面形式、壁厚系数β为0.6的有限元实体模型，其f1为0.117 Hz，而理论计算值为0.112 Hz，比前者减少了0.005 Hz。第一阶频率误差最大的是正方形截面形式、壁厚系数β为1的有限元实体模型，其f1为0.153 Hz，而理论计算值为0.138 Hz，比前者减少了0.015 Hz。总体看来，误差都在允许范围内。

从表4可以看出，3种不同截面形式钢筋混凝土空心墩理论计算模型的前三阶频率随着壁厚系数的增大而降低。这验证了前面的理论推导结论。

4 结论

本文研究了壁厚因素对钢筋混凝土空心高墩振动特性的影响。通过对不同壁厚系数β的钢筋混凝土空心高墩实体模型、线单元模型、理论模型计算结果对比分析，得出以下结论。

1)当墩高、截面形式确定时，通过理论公式推导出，钢筋混凝土空心墩的模态频率fn是关于壁厚系数β的一元函数，且该函数是单调递减函数，即随着壁厚系数β的增大，钢筋混凝土空心墩的模态频率fn降低。

2)随着壁厚系数β降低，空心高墩的质量大幅度降低,自振频率fn却微小幅度提高。这在工程设计中有比较大的指导意义，在满足安全承载力的前提下，减少壁厚，不仅节省材料，而且对结构的整体刚度影响不大，这也是目前高墩大跨桥梁多采用薄壁空心墩的原因之一。

3)通过对比实体模型和线单元模型计算结果发现：薄壁空心高墩结构可以采用线单元模型计算其前几阶自振频率，不仅可以避免实体模型建立复杂、网格划分容易出现畸变的问题，还可以大幅度缩短计算时间，误差也在允许范围内。

4)通过对比实体模型和理论模型计算结果发现：基于欧拉-伯努利梁理论的理论计算模型可以简化的计算薄壁空心高墩结构前几阶自振频率，其计算的第一频率一般低于实体模型数值模拟的计算值，但是误差在允许范围内。