图像局部特征匹配算法发展综述
2019-05-17林曦蕾
林曦蕾
(四川大学计算机学院,成都610065)
0 引言
图像匹配算法经过几十年的发展,产生了很多经典的算法,整体上来说可以分成四种类型[1]:基于图像灰度的图像匹配算法、基于变换域的图像匹配算法、基于模板的图像匹配算法和给予特征的图像匹配算法。基于特征的匹配算法通过提取图像中对形变、光照等具有不变性的信息,对这些信息进行描述构造描述符,之后对这些特征进行匹配,计算出图像之间几何变换的参数。基于特征的匹配算法比起基于灰度的匹配算法是用更少的信息进行匹配,从而大大提高运算速度。除此之外,特征点等局部信息对图像遮挡、形变等也有很好的鲁棒性。常见的算法有SIFT算法[2]、SURF算法[3]、ORB 算法[4]等。
1 图像特征匹配算法
1. 1 算法描述
基于特征的匹配算法主要包括特征提取、特征匹配、生成几何变换这几个步骤。特征提取是指提取出图像中具有代表性的信息,例如:图像中的角点、拐点等,提取出来的信息必须满足对尺度、旋转、光照、视角和噪声干扰等影响因素具有一定程度的鲁棒性。除此之外所提取的特征还必须具有独特性,以防止将相似的特征被误认为是相同的事物,从而造成特征的误匹配。经算法提取出来的图像特征主要由点、线和面这三种类型,其中由点构成局部特征对噪声、形变等具有较强的鲁棒性,因此当前很多的特征匹配算法选择以点作为特征。
特征匹配是指为图像中的特征寻找对应关系的过程。此过程如果只是使用暴力匹配的方法,算法的时间复杂度会很高,因此可以通过某些算法提高匹配的效率。例如,在SIFT算法中,利用测试图像中的特征点建立一棵KD-Tree,之后对于参考图像中的每一个特征点使用BBF算法[5]在测试图像形成的KD-Tree中寻找相邻的点。通过KD-Tree加BBF算法的匹配策略,使得特征匹配的速度有了大幅的提高。
在匹配的图像之间存在着一种几何变换,该几何变换可能是放射变换、透视变换等。而生成几何变换即为求这些几何变换的参数的过程,常用的算法有随机抽样一直算法(RANSAC)[6]、模拟退火算法和遗传算法等。
1. 2 尺度不变特征变换(SIFT)算法
SIFT算法是当前被广泛使用的局部特征匹配算法,该算法通过尺度空间检测极值点作为特征点,从而实现特征点的尺度不变性,之后通过特征点的周边区域内像素为特征点计算主方向,用于实现旋转不变性,最后将描述子采样区域旋转到特征点的方向,然后基于该区域构造描述符。
(1)构造DOG尺度空间
当人们与其观测的对象离得越远,则所能观察到的事物就越模糊,即尺度越大;当与对象离得越近,则事物越清晰,尺度越小。由于机器无法预先知道图像中物体的最佳尺度。因此,需要使用尺度空间模拟此过程。Koenderink[7]与Lindeberg[8]证明了空间高斯核是唯一可以模拟人眼对图像造成模糊效果的线性核,因此,通过空间高斯核构造尺度空间。其中,二维空间高斯函数表示为:

在上式中,( )x,y表示图像像素坐标,σ表示尺度因子,它决定着图像被模糊的程度。则一副二维图像的尺度空间定义为:
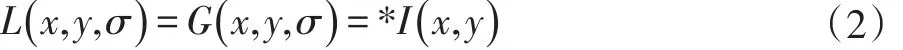
其中I(x,y)表示输入的图像,而G(x ,y,σ )表示二维空间高斯函数,*表示卷积运算。
Lindeberg在文献[9]中指出尺度规范化的LOG(Laplacian Of Gaussian)算子具有真正的尺度不变性,即让图像与LOG算子进行卷积运算,可检测出斑点(特征点)以及它的尺度。因此,用于检测特征点的是Laplacian金字塔,其中LOG算子是高斯函数的二阶偏导。
Lindeberg[10]通过研究发现高斯差分算子(Difference Of Gaussian,DOG)与尺度归一化的高斯拉普拉斯算子非常近似。由于高斯差分算子与高斯拉普拉斯算法子非常近似,且构造尺度空间的效率更高。因此,Lowe[2]提出了用高斯差分尺度空间近似拉普拉斯尺度空间:

构建高斯差分金字塔包括三个步骤:①构建多分辨金字塔,每一层通过对下一层进行下采样获得,如图1所示;②在构建的多分辨金字塔的基础上,对每一层的图像使用不同的σ进行高斯模糊,从而获得多组图像,如图2所示,在每一组位于最底层的图像,是由该组图像的下一组图像的倒数第三张降采样得到的;③对金字塔中处在同一层中的相邻图像进行相减操作,从而获得新的一组图像。

图1 多分分辨率金字塔
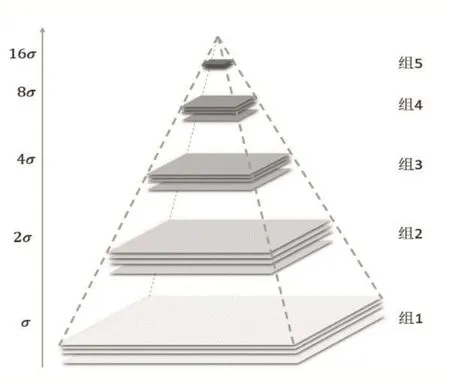
图2 高斯多分辨率金字塔
(2)极值点定位
为了检测尺度空间中的极值点,需要让尺度空间中的每一个像素与其相邻的26个像素点进行比较,选取其中最大或最小的点作为潜在的特征点。由于在离散空间中检测到的极值点存在误差,因此需要通过三维二次函数拟合来精确定位极值的位置。为了精确定位极值点的位置,首先对尺度空间函数D(x,y,σ)进行泰勒展开,如下所示:

上式中X=(x,y,σ)T。之后对上式进行求导并令其为0,通过求解式子可得精确的位置,解得:

为了去掉低对比度的点,将求得的解 X^代入D(X ),于是可得:

为了去掉边缘响应点的影响,通过Hessian矩阵来判断某处是否为边缘,若不是边缘则保留,否则剔除,其中Hessian矩阵为:

设α,β分别为Hessian矩阵的两个特征值,且α大于β,又由于特征值的和与积可以通过Hessian矩阵的迹与行列式来计算得到,则有:

设r=α/β ,则:
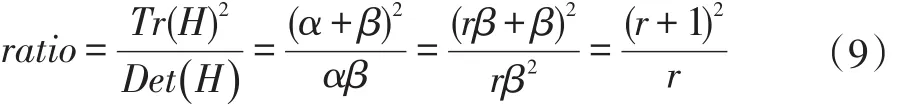
(3)分配主方向
为了实现旋转不变性,需要为检测到的特征分配主方向。首先,计算特征点的领域中每个像素点的梯度的方向和大小,然后统计领域中梯度方向的分布,选取直方图中累积梯度大小最大的梯度方向角作为主方向。领域内某个点x的梯度的方向θ(x ,y)和大小m(x ,y),可以通过以下公式得到:

(4)生成描述符
选取以特征点为中心的16×16个像素作为构造描述符的区域。在构建描述符之前,对用于构建描述符的区域按主方向的角度执行旋转操作,如图3所示。将旋转之后的区域划分为4×4个子区域,在每个子区域中统计8个方向的直方图,每个方向为45°,如图4所示,左边部分将窗口划分为4×4个子区域,每个子区域由4×4个像素点组成,并标出每个像素的梯度方向和大小,右边部分每个子区域表示8个方向以及每个方向的梯度大小累积和。最后,用每个子区域中的梯度大小累积和构成一个向量,此向量为4×4×8=128维,其即为特征点的描述符,为了消除光照变化的影响,还要对特征向量进行归一化处理。
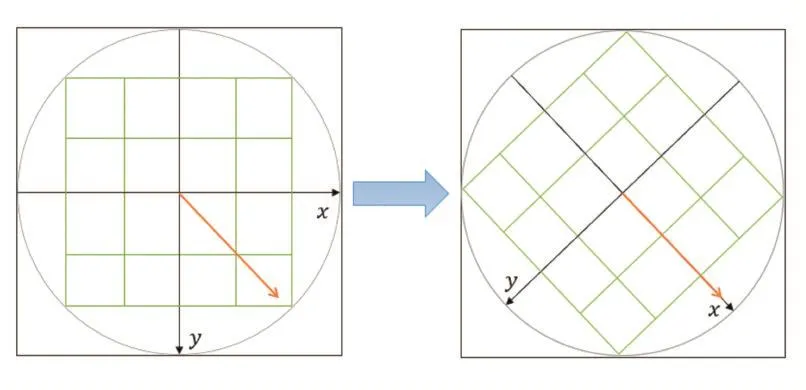
图3 对描述符构造区域执行旋转操作

图4 构造描述符
(5)特征匹配
当为特征点构造完描述符之后,通过相应的特征相似度度量方法计算特征之间的相似度,从而判断两幅图像中的特征是否匹配。
2 评价方式
在图像匹配中,常用的是文献[11]提出的特征点检测提取和匹配结果的评价准则。
对于特征点检测提取,评价优劣常常用到Repeatability(重复率)这个概念。图A、B是两幅待匹配图像,图A映射到图B有一个单应性矩阵H1,图B映射到图A有单应性矩阵H2,图A检测出N1个特征点,图B检测出N2个特征点,因为图像A和B有部分图像不重叠,故将A图检测的特征点坐标由H1算出在B图的坐标,去掉不合格(计算结果超出在B图像坐标)的特征点,剩下的特征点数记为n1;同样,B图的特征点经过处理剩下n2个;分母便是min(n1,n2)。将图A剩下的特征点由H1计算出在图B中的坐标,与图B检测出的特征点的坐标求距离,即dist(h1*a1,b1),若距离小于阈值ε,则认为是重复的,这么做是因为得到的单应性矩阵不一定完全精确以及一些别的误差原因。
特征点匹配的评价首先应当知道两个图像间的单应性矩阵H,然后通过特征点检测算法得到左右图像中的特征点信息,根据单应性矩阵得到重复特征点对,记为M;接着由特征点匹配算法计算正确的匹配点对和错误匹配点对,分别记为N、K;绘制N/M和K/(N+K)曲线,其中曲线靠上方的结果较出色。
3 结语
基于局部特征的匹配算法给图像匹配等领域带来了不一样的活力,而后续的相关算法的改进使得这个领域的算法具有更好的鲁棒性,能够更好地运用到诸如三维表面重建、立体视觉等领域。本文主要按照图像特征匹配算法的发展史和其具有代表性的经典算法,介绍了它相关的理论和评价方法。但是该领域仍然存在许多问题没有完美解决,例如在几何形变较大的匹配场景中,如何提高特征检测子以及描述符的几何不变性仍然需要深入研究。
