星敏感器安装误差标定技术研究
2019-05-16蔡善军吴亮华胡奇林
王 欣,蔡善军,吴亮华,胡奇林
(北京自动化控制设备研究所,北京 100074)
0 引言
星敏感器(以下简称星敏)是一类具有独立自主高精度姿态测量能力的仪器,目前三轴测姿精度可达到角秒级[1],输出的惯性姿态误差不随时间累积,数据更新率可达5~10Hz。在长航时飞行器应用背景下,可利用星敏高精度的姿态信息修正惯性导航的误差[2],实现高精度自主导航。大视场星敏感器技术的发展,使得星敏与惯导系统采取捷联安装的方式成为可能。受加工精度的限制,星敏与惯导系统之间的安装误差常常能达到角分级[3]。而诸如岁差、视差等因素使恒星方向有微小的变化,从而造成星敏感器的测量误差,但是它们所造成的误差是角秒级的[4]。相较而言,星敏安装误差成为限制星敏测量精度的主要因素之一。因此,有必要对星敏的安装误差建模,并进行标定补偿。
目前,星敏安装误差标定的方式有两类:一类是依靠外部基准姿态信息与星敏姿态信息进行比较从而得出安装误差角,如文献[5]提出的一种在高精度星模拟器辅助下的星敏感器安装误差标定方法,该方法采用经纬仪提供的外部方位信息,能达到10″的标定精度,但操作过于繁琐,对设备要求高,不利于在地面实现快速标定;另一类是依靠星敏的测量信息,建立卡尔曼滤波模型,对安装误差角进行估计,如文献[6]、文献[7]、文献[8],但文献中均未论述惯导姿态误差与星敏安装误差角的关系。
针对上述情况,本文从理论上分析了星敏安装误差角与惯导姿态误差的关系,利用惯导输出的姿态信息、位置信息以及星敏测量信息构造观测量,建立了卡尔曼滤波模型,实现了星敏安装误差角在地面上的标定补偿。
1 参考坐标系
设星敏理想坐标系为O-XcYcZc,载体坐标系为O-XbYbZb,星敏理想坐标系与载体坐标系方向相同;星敏实际坐标系为O-Xc′Yc′Zc′。假设星敏与惯导刚性固连,即不考虑挠曲变形,则c′系相对c系有3个小角度的安装误差角:αX、αY、αZ,则c系可通过绕Y、Z、X轴3次转动与c′系重合,因此c系与c′系之间的转换矩阵可表示为
(1)
惯性坐标系(i)与地球坐标系(e)可以通过格林尼治恒星时(Greenwich Sidereal Time,GST)联系起来,即
(2)
导航坐标系选择北天东地理坐标系(n),n系与e系的转换关系,需要使用当地的经度(λ)和纬度(φ),即
(3)
由惯导提供的经度(λc)和纬度(φc)所确定的坐标系为计算地理坐标系(nc),设惯导经纬度与真实经纬度仅存在小角度误差:δλ、δφ,于是nc系与n系的转换关系可表达为

(4)
依靠惯导输出姿态确定的地理坐标系(np)相对真实的地理坐标系(n)有3个误差角:φN、φU和φE。由于这3个角均为小量,故np系与n系的转换关系可以表达为
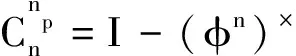
(5)
2 惯性/星光组合导航方案
在现代姿态匹配方法中,通常利用主、子惯导姿态阵的乘积来构造观测量[8]。借鉴这种思想,将天文导航提供的姿态矩阵作为主惯导的姿态阵,而惯导系统实时解算的姿态矩阵作为子惯导的姿态阵。本文设计的惯性/星光组合方案如图1所示。

图1 惯性/星光组合导航方案Fig.1 SINS/CNS integrated navigation scheme
星敏可输出星敏坐标系相对惯性参考坐标系的3个欧拉角或者姿态矩阵。输出中包含安装误差角,则有
(6)
惯导输出的姿态矩阵为
(7)
2个姿态阵不在同一个参考系下,故不能直接用于匹配。可以将惯导输出转换至惯性坐标系下,也可将星敏输出转换至地理坐标系中。两种办法实质一样,本文采取前者
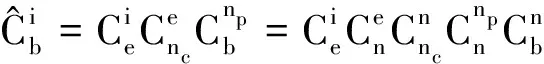
(8)
GST=ωieΔt
(9)
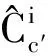

(10)
(11)
由式(10)、式(11)可知,观测量中包含三种误差源:惯导的姿态误差、惯导的位置误差和星敏感器的安装误差。由于三种误差权重相当,给误差分离带来了困难。在地面标定的过程中,位置误差较小,观测量中可只考虑姿态误差与安装误差的贡献。
对于状态变量,考虑惯导的位置误差、速度误差、失准角、陀螺漂移以及星敏的安装。由于单独的姿态匹配算法无法估计加表零位,因此可不予考虑状态变量,将其计入未建模误差。因此,惯性/星光组合导航系统的状态变量为
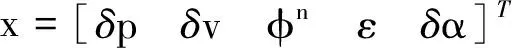
(12)
位置误差方程为
(13)
速度误差方程为
(14)
φNfE-φEfN
(15)
φUfN-φNfU
(16)
姿态误差方程为
(17)
(18)
(19)
量测方程为
Zdcm=Hx+w
(20)
其中
(21)
以上,建立了惯性/星光组合导航系统的卡尔曼滤波模型。
3 仿真分析
为验证算法的有效性,本文设计了两种不同的载体轨迹,并进行数学仿真,如表1所示。

表1 两种不同的载体轨迹
初始误差:初始水平失准角为0.01°,方位失准角为0.05°;初始经纬度误差为5m,高度误差为1m。星敏三轴安装误差均为60″。
轨迹总时长为1200s,星敏在150s以后开始工作。滤波周期与星敏姿态输出周期相同,均设置成1s。限于篇幅,以下仅给出某一次蒙特卡罗仿真结果。
由图2和图3易见,在载体无姿态机动的条件下,滤波器对星敏安装误差角的估计作用并不强,也无法对初始姿态误差进行估计。由图4可以看出,这种情况下,陀螺漂移的估计效果也不理想。
由图5可以看出,当载体进行滚转机动以后,星敏y方向与z方向的安装误差能快速估计出来,并且快速收敛。由图6易见,直到载体进行航向机动,x方向的安装误差才得以估计出来。另外结合图5、图6、图7可以发现,失准角与安装误差角存在耦合关系:只有当安装误差角估计出来,对应轴向上的失准角才能得以估计。对比图4和图8,情形二对于陀螺漂移的估计作用优于情形一。
对于情形二,进行20次蒙特卡罗仿真,星敏三轴安装误差角标定精度(σ)如表2所示。

图2 情形一安装误差角估计值Fig.2 Condition 1: estimation of installation error angle
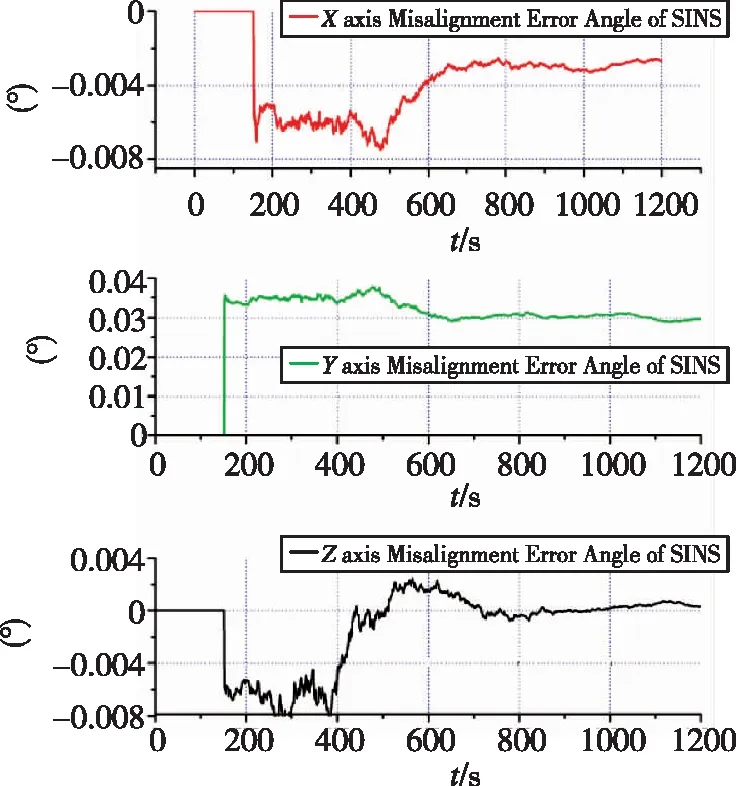
图3 情形一失准角估计值Fig.3 Condition 1: estimation of misalignment error angle

图4 情形一陀螺漂移估计值Fig.4 Condition 1: estimation of gyro drift

图5 情形二载体滚转轴运动与安装误差角关系Fig.5 Condition 2: relationship between rolling angle ofbody and estimation of installation error angle of star sensor
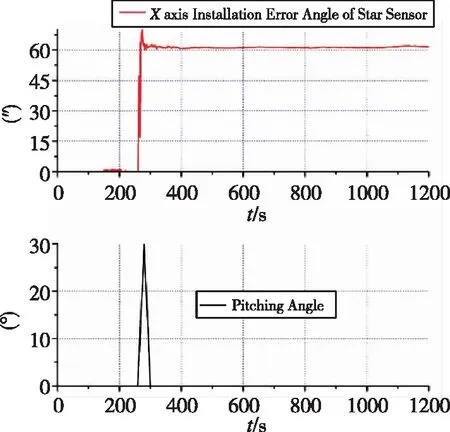
图6 情形二载体航向轴运动与安装误差角关系Fig.6 Condition 2: relationship between pitching angle ofbody and estimation of installation error angle of star sensor
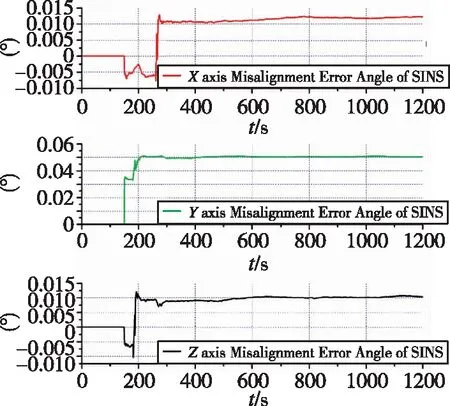
图7 情形二失准角估计值Fig.7 Condition 2: estimation of misalignment error angle
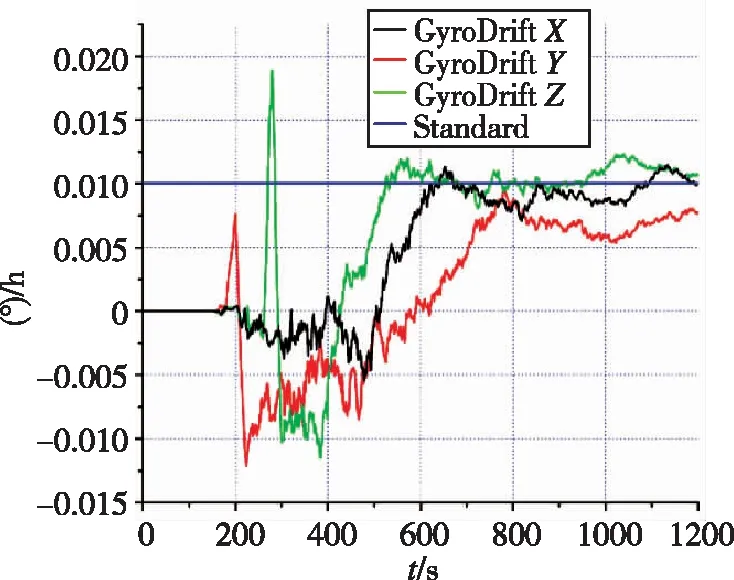
图8 情形二陀螺漂移估计值Fig.8 Condition 2: estimation of gyro drift

轴向XYZ精度/(″)8.1212.909.24
4 结论
1)本文建立了惯性/星光组合导航的卡尔曼滤波模型,从模型可以看出,惯导姿态误差与星敏安装误差角之间存在耦合关系,且对于观测量的贡献权重相当;
2)本文设计了两种仿真情形对算法进行验证。从仿真结果可以看出,当载体进行姿态机动时,组合导航方案能够估计出与姿态输入轴正交的另外2个轴向上的安装误差角。因此,估计出星敏3个轴向上的安装误差角需要载体进行2个方向上的姿态机动;
3)从安装误差标定精度可以看出,本文设计的方案与依靠外部姿态基准的方案相比,精度相当,但本文的方案标定速度快、可操作性强。
4)本文通过仿真论证了地面标定星敏感器安装误差角的可行性,为后续进一步通过地面实验验证奠定了理论基础。
