北斗空间信号误差统计特征及描述方法研究

2019-05-16刘媛媛

导航定位与授时 2019年3期

冯帅，李亮，程春，刘媛媛

(哈尔滨工程大学自动化学院，哈尔滨 150001)

0 引言

卫星导航定位技术是以卫星技术和通信技术为基础，利用导航卫星发送导航定位信息为目标用户提供测距和授时服务。继美国的全球定位系统(Global Positioning System，GPS)和俄罗斯的全球卫星导航系统(Global Navigation Satellite System，GLONASS)之后，中国的北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)成为世界上第三个面向全球提供服务的卫星导航系统。BDS在卫星导航市场面临着GPS和GLONASS的竞争与挑战，系统的性能即成为决胜市场的关键。对于实时导航的用户而言，广播星历是其能够正常导航定位的前提，而广播星历中卫星轨道和时钟的精度是影响导航定位精度的重要因素[1]。

空间信号误差(Signal-In-Space Errors，SISEs)反映的是与卫星有关的误差，主要由卫星轨道和卫星时钟误差组成，其大小将会影响导航用户的定位精度及可靠性。用户测距误差(User Range Error，URE)是广播星历轨道和卫星时钟误差的综合体现，指在接收机到卫星视线方向上的投影，反映了空间信号的精度，并最终影响实时导航用户定位精度。用户测距精度(User Range Accuracy，URA)用来描述URE的精度。Zhang等通过一个月广播星历的SISE统计分析，与武汉大学精密星历相比，得到中地球轨道卫星(Medium Earth Orbit，MEO)、倾斜地球同步轨道卫星(Inclined GeoSynchronous Orbit，IGSO)和地球同步轨道卫星(Geostationary Earth Orbit，GEO)的轨道URE值分别为0.5m、0.6～0.8m和0.9～1.8m[2]。毛亚等统计了广播星历轨道误差1d的均方根(Root-Mean-Square，RMS)和卫星时钟误差的标准差(Standard Deviation，STD)，结果表明多数卫星时钟误差精度优于10ns，轨道精度优于5m。若URE的分布服从零均值正态分布，那么URA就可表示为URE的1-sigma界限[3]。Walter和Blanch已经证明，GPS SIS URE的URA值为2.4m，GPS SIS URE的精度可由其URA准确描述[4]。对于BDS，Liu等通过分析2013年3月到2016年9月的数据发现，北斗广播星历播发的2.0m的URA过于乐观地描述了北斗URE的精度，能够满足URE 1-sigma界限的URA应为2.4m[5]。

本文利用2018年1月到6月的导航数据进行BDS空间信号误差的统计特征研究，分析了影响空间信号误差的因素，建立了北斗URE的描述方法，并验证了广播星历播发的URA是否适用于BDS。

1 SISE计算

对空间信号误差的研究主要是针对卫星轨道误差和卫星时钟误差的研究。在利用内插对比法进行星历对比前，首先要统一时空基准，然后计算时钟和轨道误差。

1.1 轨道误差

进行轨道对比时，首先要统一空间基准。主要包括两部分：

1)统一坐标参考框架。通过比较广播星历和精密星历来计算SISE，必须确保广播星历和精密星历参考坐标系的一致性。北斗广播星历轨道参考2000国家大地坐标系(China Geodetic Coordinate System 2000，CGCS2000)，精密轨道参考IGS14坐标系(The International GNSS Service 14，IGS14)，但这2个框架相差在几厘米之内，对于米级的轨道误差影响极小[6]，所以在对比过程中忽略坐标系统的差别。

2)校正天线相位中心。精密星历以卫星质心为坐标零点，而广播星历以天线相位中心为零点。所以，在比较广播星历和精密星历之前，通常进行天线相位中心偏移校正。修正参数来源于igs14_1949_plus.atx文件。

由于广播星历和精密星历都基于地心地固坐标系(Earth-Centered，Earth-Fixed，ECEF)，而本文研究的是卫星导航系统的空间部分。由于在卫星轨道坐标系(Radial-Along-Cross，RAC)下可以更明确地展现出卫星的运动特性，因此在进行统计之前，本文将ECEF坐标系下的各向误差转换到RAC坐标系下进行计算[7]。

设P1,P2,…，Pn为某颗卫星在某个等差时间段内的已知位置，可通过8阶拉格朗日多项式内插法计算出该卫星在这个时间段内的任意时刻的速度[8]。由位置向量和速度向量可求出单位方向向量。

(1)

其中，ei是单位方向向量(i=radial,along,cross)，Δx、Δy、Δz分别为ECEF坐标系下的轨道径向、切向和法向误差，R、A、C分别为RAC坐标系下的轨道径向、切向和法向误差。

1.2 卫星时钟误差

北斗广播时钟Tb以单频B3I信号为参考。然而，本文选用的德国地球科学研究中心(GeoForschungsZentrum，GFZ)发布的北斗精密时钟产品Tp是通过使用双频(B1I和B2I)无电离层组合计算得到的，因此，应移除14s的BDT-GPST偏移量。在比较Tb和Tp之前，还应考虑时间群延迟(tgd)[9]：

(2)

(3)

(4)

由于在Tb和Tp的计算过程中采用了不同的参考原点，因此为了获得正确的广播卫星时钟误差，还应该去除公共时间尺度偏差。在历元k的卫星i的时间偏移量可以表达为

(5)

其中，μ(k)是在历元k处的公共时间尺度偏差；δTi(k)是卫星i的广播时钟误差;Δi(k)是噪声。通过加权最小二乘方法可以估计公共时间尺度偏差

(6)

在估计共同时间尺度偏差之后，卫星时钟误差通过以下计算得到

(7)

2 北斗URE描述方法

BDS卫星轨道和时钟的解算方式不同于GPS，所以在计算北斗URE时不能完全套用GPS URE的描述方法，必须针对BDS的特点对传统URE的描述方法加以修改，使其能够恰当准确地描述BDS的URE。

2.1 瞬时用户测距误差

瞬时用户测距误差(Instantaneous SISURE，IURE)就是指某一时刻的瞬时URE。北斗IURE计算公式为

(8)

2.2 全球平均用户测距误差

地球上不同地点的GNSS用户会遇到不同的UREs。为衡量空间信号整体上的精度，综合轨道误差和卫星时钟误差，提出了全球平均用户测距误差(Global-Average URE，avgURE)。对于GPS，avgURE由式(9)计算

(9)

式中，A表示轨道的切向误差，C表示轨道的法向误差。(R-δT)代表着卫星时钟误差和径向轨道误差之间具有负相关性，这是由GPS的轨道和卫星时钟误差解算算法决定的。然而，北斗采用双向卫星时间、频率传递(Two-Way Satellite Time and Frequency Transfer，TWSTFT)方法来确定卫星时钟。TWSTFT测量卫星和地面站之间的下行和上行伪距观测值，以计算相对于地面主时钟的卫星时钟误差。该方法将卫星时钟与轨道分开估算。因此，北斗径向轨道误差与卫星时钟误差之间的相关性并不显著。同时由于BDS卫星轨道高度与GPS轨道高度不同，因此BDS的URE的计算可区别如下。

对于GEO/IGSO卫星

(10)

对于MEO卫星

(11)

avgURE涉及轨道误差和卫星时钟误差，是轨道误差和卫星时钟误差的综合体现。

2.3 轨道部分的用户测距误差

根据式(10)和式(11)，在不考虑卫星时钟误差的情况下，轨道部分的用户测距误差(Orbit-only URE，OrbitURE)公式为

(12)

(13)

OrbitURE是将轨道误差和卫星时钟误差进行误差剥离，仅考虑轨道误差在计算avgURE时的作用，为下面分析轨道误差和卫星时钟误差何者在计算avgURE时占主导地位奠定了基础。

2.4 最差用户测距误差

就SIS完好性而言，最差用户测距误差(Worst-case URE，worstURE)对评估SIS性能至关重要。对于BDS，卫星时钟误差与径向误差之间没有显著相关性。因此，卫星时钟误差和径向误差被独立传播到最差SIS URE[10]。因此，北斗worstURE的公式可以用式(14)来描述

worstURE=

(14)

本节根据北斗独有的卫星时钟误差测定方法会导致卫星轨道径向误差和卫星时钟误差之间相关性较弱这一推论，对GPS的URE描述方法进行了修改，使之符合BDS空间信号误差的特点。相比于直接套用GPS的URE计算公式，修改后的描述方法可以更准确地描述BDS的URE，更加简洁的公式也有利于之后对其统计特征的分析。

3 实验结果及分析

实验首先基于内插对比法分析了北斗卫星轨道和卫星时钟误差的变化规律及精度。为了探究轨道误差和卫星时钟误差对于SISRE的影响，验证SISRE描述方法修改的正确性，以及确定适合描述SISRE的URA，实验还对北斗空间信号误差的统计特征进行了分析。

3.1 广播星历和精密星历数据源以及数据预处理

本文采用的广播星历和精密星历来源于多GNSS实验网(Multi-GNSS Experiment，MGEX)(ftp://cddis.gsfc.nasa.gov/，广播星历数据为brdm0010.18p到brdm1820.18p，精密星历sp3数据为gbm19821.sp3到gbm20080.sp3，精密星历clk数据为gbm19821.clk到gbm20080.clk，数据时间跨度为6个月)。基于内插对比法，以GFZ提供的精密轨道和时钟作为真值，分析从2018年1月1日到2018年6月30日的广播星历轨道和卫星时钟误差。为保证样本独立性，采样率选为15min。同时在比较广播星历和精密星历之前，应排除2个数据集中的无效星历。无效星历可用以下条件筛选[11]：

1)导航信息不健康，即健康状态字为1。

2)|tk-Toe|>1h或|tk-Toc|>1h。其中tk是历元k的时间，Toe是星历参数的参考时间，Toc是时钟参数的参考时间。

3)精密星历/时钟坏值或缺失被设置为“0.000000”/“999999.999999”。

3.2 钟轨误差分析

图1展示了C01、C06和C11号卫星广播星历的轨道误差。

图1 北斗卫星轨道误差图Fig.1 BDS orbit error

C01号卫星为GEO，GEO为地球同步轨道卫星，其轨道周期等于地球的自转周期，为23h56min4s。为了得到轨道变化的一些细节，图1给出了C01号卫星1月1日到11日的轨道误差图。从放大图中可以看出，轨道径向、切向和法向的误差变化都具有周期性，而且三者的变化具有一致性，周期大约为24h，这也与GEO的轨道周期相符。

C06号卫星为IGSO，IGSO是倾斜地球同步轨道卫星，与GEO一样，其轨道周期等于地球的自转周期，约为24h。与C01号GEO相比，C06号卫星的轨道误差明显要小，尤其是切向和法向误差。从放大图中可以看出，三向误差具有相同的变化周期，轨道径向和切向误差变化具有一致性，而法向误差变化落后径向和切向半个周期。

C11号卫星为MEO，MEO是中地球轨道卫星，运转周期约为12h。与其他两类卫星相比，MEO的轨道误差最小。从放大图中可以看出，3个方向上的轨道误差都具有一定的周期，大约为12h。图中还展示出了另一个大约7d的周期。在这个周期内，轨道三向误差的变化具有一致性。

图2展示了北斗三类卫星的时钟误差。从图2中可以看出，GEO的时钟误差在5m以内，大多为负值；IGSO的时钟误差在3m以内，大多为正值；MEO的时钟误差在2m以内，大多为负值。整体来看，MEO的时钟误差最小，IGSO次之，GEO的时钟误差最大。

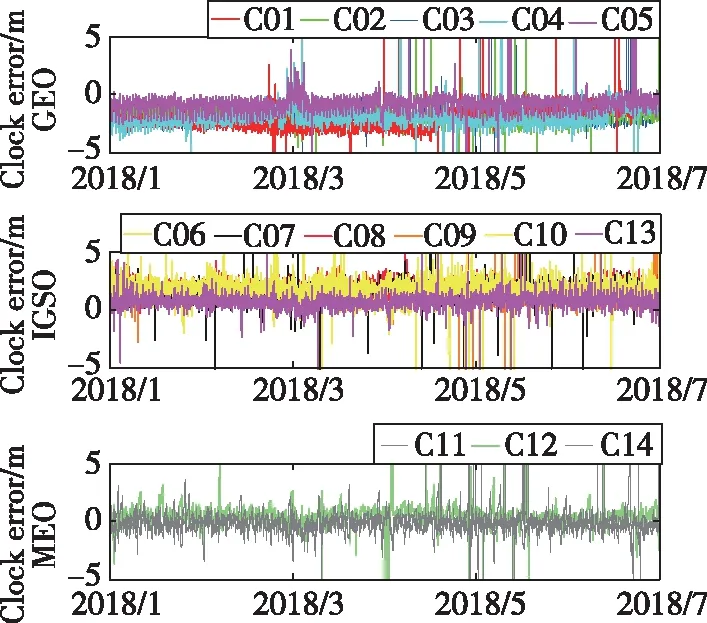
图2 北斗卫星时钟误差图Fig.2 BDS clock error

图3展示了三向误差的均值和标准差。从图3中可以看出，在径向上，GEO、IGSO和MEO可近似为零均值，三类卫星的标准差都较小，在1m以内；在切向上，三类卫星均值围绕零值上下波动，幅度较小，但是GEO标准差较大，达到了4m；在法向上，三类卫星均值都接近0，但标准差差距比较明显。GEO标准差最大能达到7m，IGSO标准差最大为1m，MEO标准差则在1m以内；对于卫星时钟误差，大多数卫星时钟误差不具有零均值，但标准差都小于1m。较小的标准差说明其波动较小，稳定性好。从图4中也可以看出，整体上，MEO的轨道精度最高，IGSO次之，GEO轨道误差最大。

图3 轨道三向误差的均值和标准差Fig.3 Mean and STD for RAC

图4 轨道三向误差和卫星时钟误差均方根Fig.4 RMS for RAC and clock error

3.3 URE的统计特征

统计特征的分析对于评估系统的整体性能起到了十分重要的作用。对于统计特征的研究主要包括以下4个方面[12]：

1)计算SISRE的均值、标准差和均方根值，分析轨道误差R、A、C和卫星时钟误差δT在计算SIS URE时的权重；

2)计算每个卫星的轨道误差R、A、C和卫星时钟误差δT之间的相关系数，以此证明之前对于BDS SISRE描述方法修改的正确性；

3)通过对峰值和偏度值的分析验证IURE的分布是否满足正态分布；

4)为了研究URA能否正确描述SISRE，将avgURE和worstURE的经验累积分布函数与当前给出的URA进行比较，并结合URE的RMS值，确定当前适合描述BDS的URA值。

图5展示了轨道误差和卫星时钟误差之间的相关性。从图5中可以看出，A-R之间基本为负相关，C-R之间相关性较大，A-T和C-T之间相关性很弱。A-R、A-C、C-R、R-T中C10相关性较大。除了C10，R-T之间也是弱相关，从而验证了式(10)、式(11)对于avgURE的修改。

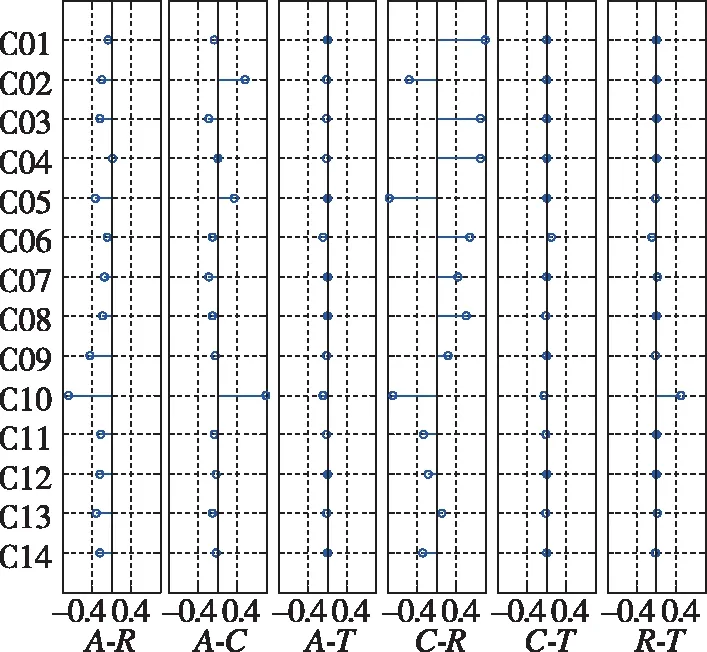
图5 轨道和卫星时钟误差相关性图Fig.5 Orbit and satellite clock error correlation graph

假定URE服从零均值正态分布，则URA是对URE的1σ估计，68%的URE应处于以URA为上边界的区域中[13]。从图6中可以看出，对于GEO、IGSO和MEO，若URE的分布服从零均值正态分布，则1σ上界分别为4.1m、2.4m和1.3m。

图6 全球平均URE和最差URE的经验CDF图Fig.6 Empiricial CDF of global averageURE and worst-case URE

但是如果URE的分布服从非零均值正态分布，那么利用1σ的URE界限确定URA是不合理的。为了验证BDS的URE是否服从零均值正态分布，以GAMG测站为例，对其IURE统计特性进行分析。为了尽可能准确描述IURE的分布，在分析IURE分布之前剔除异常值。本文以4.42倍URAUB为门限值剔除异常值，其中URAUB表示广播星历播发URA的上边界。图7展示的是GAME测站GEO卫星的IURE频率分布直方图。图中蓝色区域是卫星IURE的直方图，红线是IURE的正态概率分布拟合曲线。从图7中可以看出，C01、C04和C05号卫星存在较为明显的侧偏。

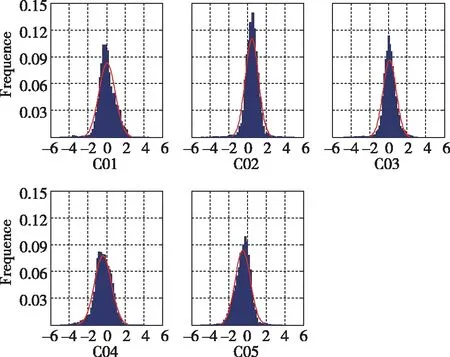
图7 GEO卫星IURE频率分布直方图Fig.7 GEO satellite IURE frequency distribution histogram

从图8的IGSO卫星IURE频率分布直方图中可以看出，C07和C09号卫星存在侧偏，所有IGSO卫星IURE均值都不为0。

图9中，C11和C14号卫星存在侧偏。另外，图8、图9中拟合的正态分布曲线均值明显都不为0。

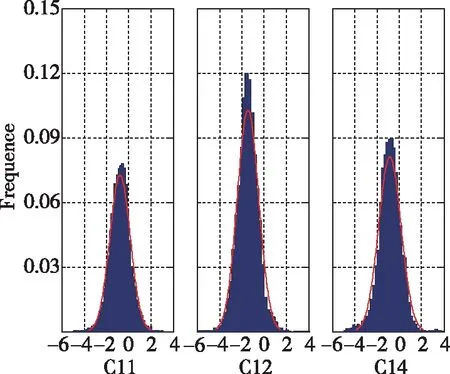
图9 MEO卫星IURE频率分布直方图Fig.9 MEO satellite IURE frequency distribution histogram

为了进一步研究IURE的分布特性，图10展示了IURE的峰度与偏度。峰度是研究数据分布陡峭或平滑的统计量，正态分布的峰度视为0。偏度是描述数据分布对称性的统计量，正态分布的偏度为0。从图7可以看出，IURE的峰度均大于0，曲线较为陡峭；大部分卫星IURE的偏度值达到了0.5，个别卫星超过1，说明IURE的分布存在一定的侧偏，曲线对称性较差，不满足正态性。所以，将URE的分布假定为零均值正态分布并不是十分合理。因此，本文选择利用URE的均方根来确定URA。

图11展示了每颗卫星和每类卫星URE的RMS值。从图11中可以看出，GEO、IGSO和MEO的OrbitURE分别为1.3m、0.8m、0.6m。对于所有卫星，OrbitURE为1.0m。

图10 IURE分布的峰度与偏度Fig.10 Kurtosis and skewness of IURE

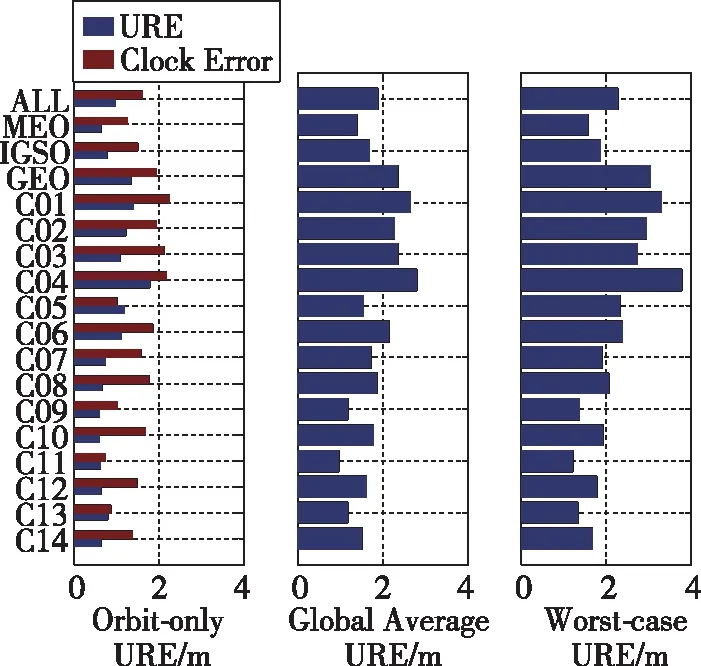
图11 全球平均、仅轨道、最差URE和卫星时钟误差的RMS图Fig.11 RMS for global average， orbit-only， worst-caseURE and clock error

为了探究钟差对avgURE的影响作用，图11将δT和OrbitURE的RMS值进行比较。结果表明，与OrbitURE相比，δT的RMS值与avgURE的RMS值更为相近，最大差值仅为0.6m，而OrbitURE与avgURE的RMS值之差最大可超过1m。由此可以推断出在avgURE的计算过程中，轨道误差所占权重较低，尤其是切向和法向误差。虽然径向误差所占权重大，但其量级小，在avgURE中的作用并不明显。所以这三者对于avgURE的计算结果影响较少，URE的大小由卫星时钟误差δT主导。

worstURE代表最差情况下的URE，也就是某一时段内URE的最大值。从完好性方面考虑，应用worstURE的RMS确定URA[14]

URAi=rms(worstUREi)

(15)

其中，i=GEO,IGSO,MEO。对于GEO、IGSO和MEO，根据式(15)，从图11中可以看出其对应的URA分别为3.0m、1.9m和1.6m。