基于有限体积法的河网水动力并行计算模型

宋利祥，李清清2，胡晓张，杨 芳，陈文龙

(1.珠江水利科学研究院，广州 510611; 2. 长江科学院 水资源综合利用研究所，武汉 430010)

1 研究背景

近十余年来，二维、三维水动力数学模型得到了不断发展和完善，但考虑到计算效率和参数率定的便利性，一维水动力模型在流域尺度河网数值模拟中仍得到了最广泛应用[1-4]。其中，Preissmann隐式差分格式[5]与分级解法[6-7]是最为经典的河网水动力模型求解方法。陈炼钢等[8]基于Preissmann四点偏心隐式差分的三级河网算法，建立了闸控河网水动力学模型。针对传统Preissmann方法不适用于跨临界流和间断流态模拟问题，吴晓玲等[9]提出了复杂流态自适应模拟模型，实现了急缓流态交替的陡坡河道水动力模拟。朱德军等[10]提出了汊点水位预测-校正法，实现了河网计算中各河道的数值解耦，避免了分级解法存在初始解不合理容易导致计算崩溃的问题。张大伟等[11]采用Godunov型有限体积离散法，运用特征线理论构造汊点方程组，建立了模拟复杂河网明渠水流运动的高适用性数学模型。向小华等[12]采用通量差分裂格式离散圣维南方程组，构建了基于隐式TVD类方法的一维河网水流模型。

在一维河网水动力模型并行计算方面，王船海和曾贤敏[13]基于多线程技术实现了多CPU环境下共享内存的河网水流并行计算。由于朱德军等[10]采用Preissmann格式离散单一河道的Saint-Venant方程组，因此同一河道的不同断面仍未被数值解耦，难以直接用于循环层次的并行化。为解决该数据依赖问题，刘荣华等[14]采用MPI技术，提出了河网拆分与任务组合算法，对河网模拟中的汊点水位预测-校正步骤实现了并行化计算。张国义等[15]利用区域分解方法，将河网划分成多个子块，并将计算任务分配到不同的处理器进行多级直接数值求解。由于隐式差分格式将单一河道内各断面求解变量以递推系数的形式进行耦合，分级解法以汊点矩阵系数的形式将河网中各河道首、末断面的求解变量进行耦合，因此，在递推系数计算、汊点矩阵求解、追赶法运算等计算密集型过程中，程序循环体具有较强的数据依赖性，求解过程不具备自然的可并行性。在实现并行计算时，需要采用较为繁琐的流程设计与数据通信，以解决数据依赖性问题，避免程序变量读写的冲突与覆盖。

本文采用MUSCL-Hancock有限体积格式离散Saint-Venant方程组，运用朱德军等[10]提出的汊点水位预测-校正法处理河网汊点连接条件，建立了具有不规则断面及非棱柱型河段的复杂河网水动力模型，实现了河网中各断面、各河道的完全数值解耦。之后，进一步运用OpenMP和OpenACC编程模式分别实现了CPU，GPU并行计算，分析了不同并行计算方式的加速效果。

2 数值模型

2.1 控制方程

采用圣维南方程组作为单一河道非恒定流控制方程，即：

(1)

(2)

式中：Z为水位；B为水面宽度；Q为流量；q为旁侧入流单宽流量；A为过流面积；g为重力加速度；u为断面平均流速,u=Q/A；R为水力半径；c为谢才系数,c=R1/6/n，其中n为曼宁糙率系数。

河网中各河道之间通过汊点连接关系实现耦合，即：

Zi,1=Zi,2=…=Zi,k；

(3)

(4)

式中：下标i为汊点编号，该汊点有k条河道，其中水流流入、流出汊点的河道数分别为kin，kout。

2.2 有限体积离散

采用单元中心型有限体积法，将式(1)、式(2)在控制体上进行积分，并利用Gauss定理离散后得

2.3 单一河道求解

采用MUSCL-Hancock算法实现单一河道的有限体积求解，主要计算过程包括基于HLL近似Riemann求解器的数值通量计算、基于MUSCL方法和Minmod限制器的界面两侧变量二阶精度重构、水面梯度项处理、基于CFL条件的自适应时间步长计算等，详细求解过程见文献[16]和文献[17]，本文在此不再赘述。

需要说明的是，界面左、右侧进行线性重构的原变量为Z，Q，在界面数值通量计算过程中，界面两侧的A，B等变量重构值，必须基于水位重构值与界面处的断面地形计算得到[18]。由于断面地形定义于控制体中心，因此，在程序初始化时，需要利用已有断面地形，基于均匀过渡假设，计算控制体界面的水位与过水面积和水面宽度的关系。此外，与二维模型类似，本文采用半隐式格式处理摩阻项[19-20]，以解决极浅水深时摩阻项可能引起的刚性问题，即

(6)

其中，

(7)

2.4 河网汊点连接条件求解

运用朱德军等[10]提出的汊点水位预测-校正法处理河网汊点连接条件，其表达式为

式中：Z1为预测的汊点水位值，Z2为校正后的汊点水位值；ΔZ为汊点水位校正量；Q为汊点位置断面的流量；B，R分别为汊点位置所有断面的水面宽、水力半径平均值，均为基于汊点水位预测值的计算结果；β为系数，本文取5.0。

由式(8)可知，当预测的汊点水位偏低，导致流入汊点水量大于流出汊点水量时，汊点水位校正量>0，使校正后的汊点水位升高，进而减小流入汊点水量、增大流出汊点水量；反之亦然。因此，上述汊点水位预测-校正法的迭代计算是收敛的。

由于朱德军等[10]采用Preissmann隐式差分格式，在迭代计算时河网所有断面均需参与求解，计算量较大。而本文采用的显式有限体积方法，同一河道的不同断面被数值解耦，在汊点水位预测-校正的迭代计算时只需汊点位置的断面参与计算，可显著减小计算量，提高计算效率。

3 并行计算

由前述求解过程可知，河网中各断面、各河道被数值解耦，变量重构、通量求解、状态更新等计算密集型过程的程序循环体内不存在数据依赖性。因此，模型计算过程具有自然的可并行性，适用于多核CPU或GPU并行架构。由于基于OpenMP的多核CPU并行编程较为成熟，本文不再赘述。针对GPU并行计算，目前主要有CUDA，OpenCL，OpenACC等编程实现模式。综合考虑软件兼容性和易用性，本文选取OpenACC并行编程模式，即OpenACC编译器通过识别编译指导指令和编译指示，由编译器自动生成并行执行代码，实现CPU-GPU异构并行计算[21]。

3.1 面向OpenACC的数据结构设计

在数据组织管理方面，传统的串行计算程序通常采用面向对象的数据结构设计方法，即以结构体数组(Array of Structure,AoS)的方式定义程序变量，如图1(a)所示。在OpenACC并行编程模式中，为利用合并访存模式，使循环运算的访存操作能受益于合并访存，需要尽可能地采用数组结构体(Structure of Array，SoA)的方式，如图1(b)所示。

3.2 数据管理方法

由于CPU与GPU之间通过PCIe接口进行数据传输，数据传递耗时、低效，因此，需要最大限度减少CPU与GPU之间的数据交换，即在CPU初始化完成后，在GPU中开辟全局变量空间，并将CPU全局变量值拷贝至GPU；在kernel循环启动计算时，不再涉及CPU与GPU数据传递；仅在需要输出计算结果时，将GPU的断面水位、流量、流速等计算结果拷贝回CPU主存空间。

本文采用declare导语声明设备全局变量[21]。即利用“!$acc declare create(data array)”，程序在声明变量后的第一时间创建设备副本，只要主机副本存在，则设备副本就一直存在，直到与主机副本同时释放。采用declare导语声明设备全局变量后，任何通过使用module的程序，若循环指定为kernels或parallel并行，则相当于使用设备变量；若循环为CPU上运行，则相当于使用主机变量。主机变量与设备变量的值可能不一样，需要通过使用update导语实现主机副本或设备副本数据更新。

3.3 基于OpenACC的循环并行化实现

OpenACC并行编程模式中，与循环并行化相关的常用导语及相应指令见图2。

由图2可知，OpenACC循环并行化相关导语较少，易于编程实现。本文模型计算多为一维循环，因此，采用parallel loop导语，充分利用GPU数以千计的线程实现循环并行化。从数据依赖性方面考虑，循环可分为2种典型情况：①不存在规约及原子操作的循环；②需要进行规约的循环。图3中的(a)，(b)分别为这2种情况的并行化实现。图中加粗的语句为OpenACC指令，其他语句为原串行计算代码。由图3可知，OpenACC编程模式以一种增量的方式进行代码开发，可极大提高代码改造效率。

表1 水位、流量计算结果对比Table 1 Comparison of calculated results of water level and discharge

4 模型验证与加速性能分析

4.1 一维溃坝问题

为验证模型在处理非矩形断面、干河床等方面的准确性，考虑断面形状为三角形的一维河道溃坝问题。平底河道总长1 000 m，边坡为1∶1，不考虑摩阻力。在河道中部位置有一大坝，上游水位为1 m，下游水位分别为0 m和0.1 m。采用等距断面对河道进行均匀化离散，断面间距为1 m。

设置t=0时大坝溃决。图4中的(a)、(b)分别为下游初始水位0.1 m时，t=80 s的水位、流量计算结果，以及下游初始水位0 m时，t=45 s的水位、流量计算结果。由结果对比可知，数值解与准确解基本一致，表明模型可有效处理激波和干河床，适用于溃坝水流等具有复杂流态的洪水演进数值模拟。

图4 一维溃坝问题数值解与准确解对比Fig.4 Comparison between numerical and exactsolutions for dam-break problem

4.2 河网恒定流计算

该算例为由Islam等[22]提出的经典测试算例，被广泛用于检验河网水动力模型的计算精度。河网拓扑结构如图5所示，各河道的长度、宽度、底坡、糙率等相关特征参数见文献[22]。边界条件：上游节点1—7为恒定流量10 m3/s；下游节点14为恒定水位2.5 m。断面间距均为100 m。

图5 河网拓扑结构示意图Fig.5 Topological structure of river network

计算结果对比如表1所示。由表1可知，流量相对误差最大值为0.04%，上游水位相对误差最大值为0.13%，下游水位相对误差最大值为0.03%。验证结果表明，本模型能准确地计算河网恒定流问题，节点11的分流比计算结果基本合理。

4.3 急缓流态交替的陡坡河道水面线计算

本算例为急缓流态交替的陡坡河道水面线计算问题[9]。河道断面为矩形，河道长为1 000 m，河宽为10 m，上游固定流量20 m3/s，下游边界固定水深1.35 m，曼宁糙率n=0.02。该河段流态属于渐变过渡流态，先从缓流过渡到急流，再从急流过渡到缓流，前一个过渡形成水跌，后一个过渡形成水跃[9]。水跌时水位表现为光滑过渡，而水跃存在明显的间断点。

断面间距为10 m。图6为本模型计算结果与文献[9]计算结果对比。由图6可知，本模型计算结果与文献[9]计算结果基本一致，合理模拟了水跌及水跃形态，表明模型可用于具有急缓流态交替的山区陡坡河道水流模拟。

图6 陡坡河道水面线计算结果对比Fig.6 Comparison of water-surface profile forsteep river

需要说明的是，由于Godunov型有限体积法可处理急缓流态交替问题，而Preissmann方法需要进行特殊处理以实现复杂流态自适应模拟，因此，与文献[9]的方法相比，本文模型更易于编程实现。

4.4 珠三角河网洪水模拟

珠三角河网是世界上最复杂的感潮河网之一，河网中同时存在树状、环状结构。受潮汐与径流的双重影响，珠三角河网水动力条件极为复杂。建立了珠三角一维河网模型，河网范围如图7所示，上游边界为三水、马口、博罗、麒麟咀、老鸦岗等站的流量过程；下游边界为大虎、南沙、冯马庙等珠江八大口门控制站的潮位过程。模型包括347条河道、215个汊点和3 866个断面，断面间距为40～2 000 m。采用“2005·6”大洪水(2005年6月23日18:00至2005年7月1日6:00)对模型进行了验证。限于篇幅，本文仅给出部分站点的实测水位与计算值对比，见图8。由结果对比可知，计算水位与实测值吻合较好，表明模型参数合理。

图7 珠三角河网示意图Fig.7 River network of the Pearl River Delta

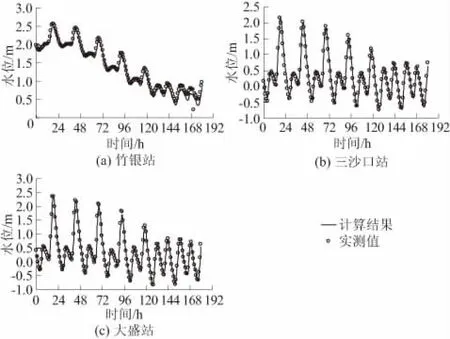
图8 典型站点实测水位与计算结果对比Fig.8 Comparison of water level at typical stations betweennumerical and measured values

为分析CPU、GPU等不同并行计算方式的加速效果，分别使用Intel Xeon(R) CPU E5-2609 v2@2.50 GHz和专业计算显卡Tesla K20(2 496个CUDA核心，时钟频率706 MHz)并行计算，对比本模型CPU多核并行、GPU并行的计算耗时，统计结果见表2。其中，加速比定义为串行模型计算耗时与并行模型计算耗时的比值。

表2 模型加速性能统计Table 2 Results of running time and speedupratio of parallel models

由表2可知，本文模型CPU并行计算(4核8线程)、GPU并行计算的加速比分别为1.51，2.63，较串行模型的计算效率得到一定提高。受益于Tesla K20的强大计算能力(双精度浮点运算峰值可达到1.17 TFLOPS)，本文GPU并行模型的加速效果更为显著。

5 结 论

本文基于MUSCL-Hancock有限体积格式和汊点水位预测-校正法，建立了断面与河道完全数值解耦、适用于不规则断面及非棱柱型河段的复杂河网水动力模型。研究了面向OpenACC的数据结构设计与数据管理方法，运用OpenMP和OpenACC编程模式分别实现了CPU,GPU并行计算。通过珠三角河网“2005·6”大洪水模拟算例，本文模型CPU并行计算(4核8线程)、GPU并行计算的加速比分别为1.51和2.63。

算例研究结果表明，模型具有良好的稳定性和计算效率，可适用于陡坡河道水动力模拟，具有较好的推广应用价值。

然而，值得注意的是，由于硬件特性决定了CPU更适合有很多分支判断的计算、GPU更适合数据密集型计算，因此，在河网结构较为简单、计算断面数量较少的情况下，CPU并行计算效率可能优于GPU并行计算。