公路混凝土桥梁疲劳寿命安全评估方法

2019-05-15赵学峰

山西交通科技 2019年2期

赵学峰

（山西省交通科学研究院桥梁工程防灾减灾山西省重点实验室，山西太原 030006）

0 引言

随着交通运输业的不断发展，公路桥梁的安全运输也成了人们关注的重点，在众多已建成或正在建设的公路桥梁中，钢筋混凝土结构占很大比重，因此，对混凝土疲劳寿命的准确评估具有重要的现实意义。多年来，国内外专家学者在结合混凝土的抗疲劳特性、剩余寿命预测等方面，对混凝土的疲劳寿命做出了众多评估与研究，也取得了许多有学术价值的科研成果，例如弹性力学评估方法[1]。这些方法虽能对混凝土结构材料进行有效的疲劳寿命评估，但偏差值较大，无法对公路桥梁等混凝土结构建筑进行准确的寿命预测，严重影响我国交通运输业的进一步发展。针对上述问题，本文提出并设计了一种基于S-N 曲线的疲劳寿命安全评估方法，并通过实验论证分析的方式，确定该方法的可行性。结果表明，以钢筋混凝土的S-N 曲线为基础，依照线性疲劳损伤累加原则对桥梁疲劳损伤程度进行分析与评估的方式，能够对公路混凝土桥梁的疲劳使用寿命进行准确评估与预测，较弹性力学评估方法具有极高的有效性。

1 基于S-N 曲线的混凝土桥梁疲劳寿命评估方法设计

1.1 构建S-N 曲线

为了准确评估混凝土结构的疲劳强度和使用寿命，本次设计引入外荷载与疲劳寿命之间的关系理论，建立能够反映混凝土应力幅值和疲劳使用寿命之间关系的曲线，这条曲线就叫做S-N 曲线[2]，如图1 所示。

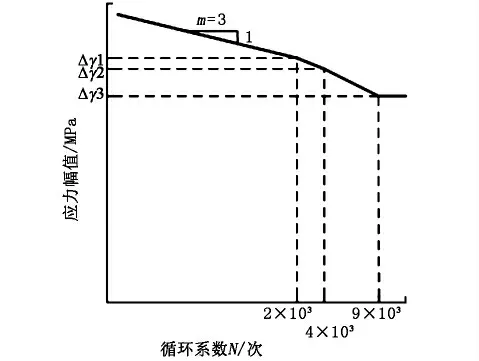
图1 混凝土S-N 曲线示意图

图1中，x 轴和y 轴均采用对数坐标，其方程表达式为：

式中：Δγ 代表混凝土的实际应力幅值；m 代表S-N曲线斜率；C 为常数，本次计算不做定向分析。

断裂力学的研究表明，在桥梁表面已经产生裂纹的情况下，小于Δγ 的应力幅值也会加大裂纹扩展面积[3]。因此本次设计将S-N 曲线的斜率调整为m+2，若实际应力幅值高于Δγ，则此时混凝土为疲劳状态，桥梁趋于不稳定状态；反之，若实际应力幅值低于Δγ，则此时混凝土结构不会产生疲劳损伤，桥梁将具有无限安全寿命。

1.2 临界裂纹尺寸确定

在上述构建的S-N 曲线内，对混凝土的裂纹过程进行模拟。首先通过无损检测方法对混凝土的裂纹形状和位置进行检测，然后根据理想化裂纹结构确定初始裂纹的简化结构[4]，在此基础上，对混凝土的裂纹结构进行描述并建立基本假定。

若实际裂纹尺寸大于初始裂纹结构时，即K≥K0，则根据S-N 曲线的力学发展，对混凝土桥梁发生脆性断裂的可能性进行计算，可得到混凝土结构临界裂纹的深度为：

式中：h 代表桥梁的临界裂纹深度；Y 代表应力强度因子。

若混凝土发生韧性断裂时，其横截面会大幅增加，同时，裂纹尺寸也会增大。当承受外荷载的横截面面积随着断裂强度的增加而减小时，断裂横截面上的应力幅值将会增大并达到最大。这一过程中，忽略其他外力作用，理想状态下认为初始缺陷截面所受到的作用力与临界裂纹截面所受到的作用力相等。则根据混凝土结构发生断裂时受到的合力，计算裂纹的半长度为：

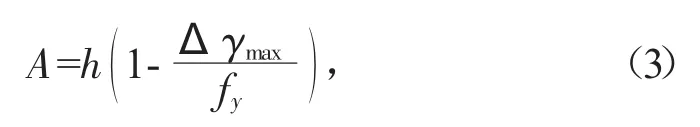
式中：A 代表混凝土裂纹半长度；fy代表裂纹拓展后的界面应力幅值；Δγmax代表作用在断裂混凝土结构上的最大应力值。

得出混凝土结构的裂纹半长度后，相对应的加上整个混凝土结构的总长，便可得到临界裂纹的具体尺寸，为下一步的安全评估计算做准备。

1.3 混凝土结构疲劳寿命评估计算

研究发现，在应力幅值作用下混凝土桥梁的使用寿命是由桥梁内部的受力情况决定的[5]，因此疲劳寿命安全评估的过程可以转化为在随机变动应力幅值的条件下，混凝土的裂纹扩展面积的计算过程。根据Paris 应力强度理论，设计如图2 所示的评估模型。

将应力强度因子的变化幅值作为描述混凝土疲劳荷载的特征性，结合图2 模型，计算其裂纹扩展面积[6]，在S-N 曲线坐标系下，裂纹扩展速率与应力强度因子的对应关系为：

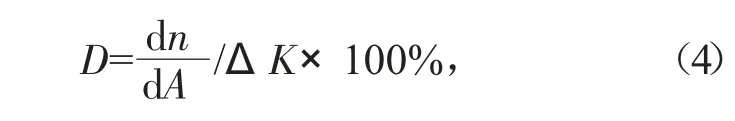
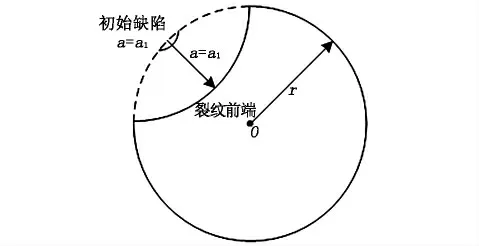
图2 基于S-N 曲线的混凝土疲劳分析模型

式中：D 代表混凝土裂纹的扩展速率，用百分比计量；n 代表混凝土结构常数；ΔK 代表裂纹均值。

分析式（4）可知，对于任意一个应力幅值，都有一个循环次数Δn 与之相对，若混凝土结构发生缺陷时，相对应的应力强度幅值不变，则必定存在一个与应力幅值相关的强度因子。只有保证应力强度因子幅值低于初始值，才能将混凝土结构的损坏情况加以制止。

由于S-N 几何修正因子是不断变化的，因此采用循环计算方法[7]，对每一层结构的应力幅值进行确定。假设裂纹的半长度为A1，相对应的强度因子幅值为ΔKm，实时监测桥梁的缺陷情况，并记录每个循环因子的应力幅值，计算对应的裂纹增量为：

式中：Δa 代表桥梁的裂纹增量，即裂纹拓展面积；Nt代表t 时刻内产生的缺陷面积。

已知桥梁的裂纹拓展面积越大，疲劳寿命的安全使用周期越长；反之，若桥梁的裂纹拓展面积越小，疲劳寿命的安全使用周期越短。则根据上述分析，能够实现对公路混凝土桥梁疲劳寿命安全的准确评估，但由于计算裂纹扩展面积时，需要反复计算裂纹扩展增量Δa，导致评估工作量过大，影响评估效率。因此本次计算采用C+语言程序[8]，将公路混凝土桥梁的初始缺陷长度、临界裂纹尺寸、应力强度因子幅值、材料断裂常数等参数均输入程序，采取均值参考系数的方法，对混凝土结构的疲劳寿命进行评估计算。

从混凝土结构裂纹萌生开始，向程序内输入初始裂纹长度，经过不同应力幅值的循环作用，对裂纹扩展增加面积进行计算，直至累加的应力幅值达到临界裂纹尺寸，这时混凝土结构将发生断裂，停止使用，那么致使混凝土发生断裂的最大应力幅值就是此次循环结构的疲劳剩余寿命。至此，完成对基于S-N曲线的公路混凝土桥梁疲劳寿命安全的评估计算。

2 实验分析

为保证本文设计的基于S-N 曲线的公路混凝土桥梁疲劳寿命评估方法的可行性与有效性，对某混凝土桥梁进行疲劳生命安全的评估。该桥梁主梁为空心板，主梁混凝土结构标号为C50，桥面混凝土标号为C50，主筋直径为20 mm，斜向跨径为10 m，梁高为0.5 m，斜交角度为40°。同时，为了保证实验结果更具说明性，采用弹性力学评估方法与本文S-N 曲线评估方法进行对比，具体实验过程及结果分析如下。

2.1 基于S-N 曲线的桥梁寿命评估实验

由于桥梁受力的不均衡性，因此在车辆荷载作用下，混凝土结构逐渐发生裂纹现象，但这一过程中，无法直接获取裂纹截面的应力幅值，故本次实验假设混凝土结构处于弹性阶段，发生裂纹时，截面应力服从理想状态下的裂纹应力。同时，认为混凝土之间没有滑移作用，不产生其他阻力，根据裂纹截面的应力幅值，得到受力混凝土结构的应力过程。

桥梁结构中，考虑到钢筋腐蚀疲劳的影响，根据上述过程，计算混凝土结构的疲劳极限值与应力强度因子，并将结果代入式（5），得出其疲劳寿命的评估值，具体结果如表1 所示。

2.2 基于弹性力学的桥梁寿命评估实验

弹性力学评估实验首先要准确测量桥梁的各个参数值，也正由于此过程的复杂程度，导致最终的评估结果偏差项过大。

参考前人的研究成果，将各个计算结果代入弹性力学评估模型中，判断混凝土应力强度因子的几何修正系数和裂纹扩展情况。若应力强度因子的几何修正系数低于初始强度值，则认为该结构存在裂纹，通过模型计算其疲劳寿命；若应力强度因子的几何修正系数高于初始强度值，则说明该混凝土结构性能良好，其剩余疲劳寿命约为50年，因此不做计算。在认为本次实验过程中混凝土结构存在裂纹的前提下，得到的疲劳寿命评估结果如表1 所示。

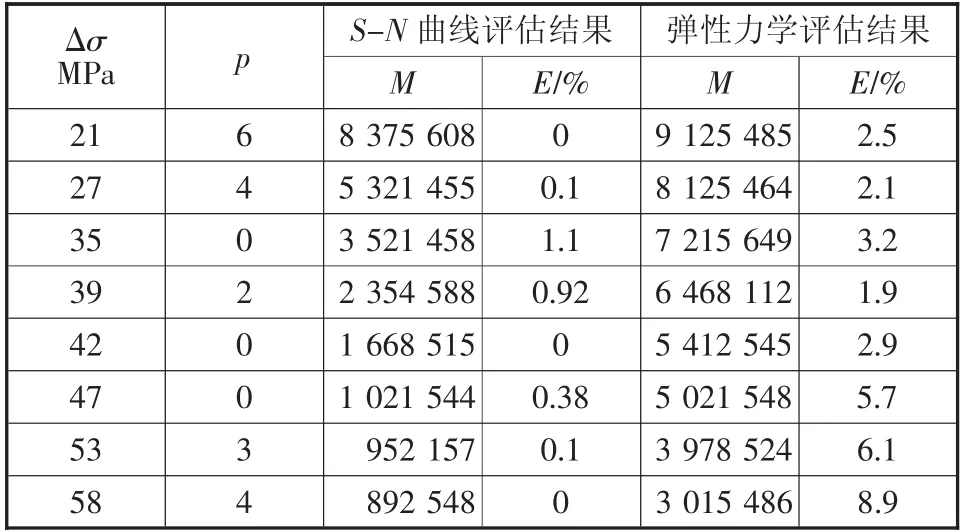
表1 桥梁疲劳寿命评估结果对比表

2.3 结果分析

根据上述两种不同方法对桥梁的疲劳寿命进行评估，得到的评估结果如表1 所示。

表1 中，Δσ 代表实验过程中混凝土所受应力幅值水平；p 代表各级应力幅值的循环次数；M 代表混凝土实际疲劳损伤评估值；E 代表评估偏差项。

分析表1 实验结果可知，采用弹性力学与S-N曲线均能完成对公路混凝土桥梁疲劳寿命安全的评估，但实际疲劳损伤估计值的大小和偏差项不同。分析可知，基于弹性力学的评估方法对桥梁疲劳寿命的估计损伤值偏高，偏差项百分比过大；而本文基于S-N 曲线的评估方法下，对桥梁疲劳寿命的损伤评估值也略高一些，但不影响最终评估结果的分析，且平均偏差项仅为0.65%，不影响实际评估结果，因此可以确定本文评估方法的有效性和可行性。结果表明，基于S-N 曲线的公路混凝土桥梁疲劳寿命安全评估方法，能够在不对混凝土结构产生疲劳损伤的前提下，对其疲劳使用寿命进行准确评估与预测。