基于布尔矩阵分解的蛋白质功能预测框架

刘 琳 唐 麟 唐明靖 周 维

1(云南师范大学信息学院 昆明 650500)2(民族教育信息化教育部重点实验室(云南师范大学) 昆明 650500)3(云南师范大学校长办公室 昆明 650500)4(云南大学国家示范性软件学院 昆明 650091)

蛋白质(protein)是组成生命体一切细胞、组织的基本有机物，是生命活动的主要承担者.根据遗传学中心法则，基因在经过转录和翻译之后才能由蛋白质在各种生命活动中执行其功能.因此，在大规模水平上对蛋白质的结构及功能进行研究的蛋白质组学对于阐明生命现象的本质和活动规律具有重要的意义，也是后基因组时代生命科学研究的核心内容之一.当前，蛋白质组学研究的一个重要内容就是对蛋白质进行功能注释.然而传统基于生物实验的蛋白质功能注释方法费时费力，无力填补基因组测序技术所获得的大量蛋白质与其功能之间的鸿沟.近年来，越来越多的生物信息学研究者利用蛋白质序列数据、基因表达数据、系统发生谱等各种类型的生物数据，针对数据特点建立相应的计算模型以完成蛋白质功能的自动注释.这类基于计算模型的蛋白质功能预测方法可以大大节省蛋白质功能注释的时间和人力消耗，因此已成为目前蛋白质组学中的一个研究热点.

从计算模型的角度看，该领域的研究大致可分为两大类：基于分类的方法和基于网络的方法.1)基于分类的蛋白质功能预测方法是将蛋白质看作需要分类的实例，而将注释蛋白质的功能术语看作类别标签，功能术语可由FunCat(funcat category)[1]和基因本体(gene ontology, GO)[2]所定义，与功能相关的各种生物数据转换为蛋白质的特征，最后利用各种多标签分类器的训练和测试来完成蛋白质功能标签预测.2)基于网络的蛋白质功能预测方法是通过网络中节点的距离来衡量蛋白质功能的相似度，可以基于蛋白质的功能关联性或蛋白质相互作用网络构建出以蛋白质为节点的网络表达[3-5].

在基于分类的蛋白质功能预测研究中，很多传统的多标签分类方法如支持向量机 (support vector machine, SVM)、神经网络和决策树等[6-10]已取得较好的预测效果.但同时，我们的大量前期研究表明：与普通的分类场景相比，蛋白质功能预测中功能注释标签数量非常庞大，如仅在文献[8]的D1数据集中就包含了4 133个GO术语.换句话说，处理蛋白质功能预测数据集的算法所面对的不再是几个或几十个标签，而是成百上千的大规模标签，这会直接导致计算模型的训练时间非常长.特别是对于一些传统的多标签分类算法，根本无法处理大规模标签分类问题，例如BR(binary relevance)方法不可用在具有104个标签的多标签分类问题中，因为这意味着它需要训练104个二值分类器.同时，已有研究表明：面对这种大量标签的多标签分类数据集，SVMs等判别式模型的分类性能会急剧下降[11].

此外，由于蛋白质功能标签之间均具有层次结构，显然被低层功能标签注释的蛋白质数量会比高层功能标签注释的蛋白质数量少很多，这种标签的标注样本频率极度不平衡的情况会直接导致分类效果不佳.图1展示了对D1数据集[8]中功能标签标注频率的统计结果.从图1中可以看出，大量的功能标签注释了非常少的蛋白质，仅仅有较少的功能标签注释了超过30个蛋白质.

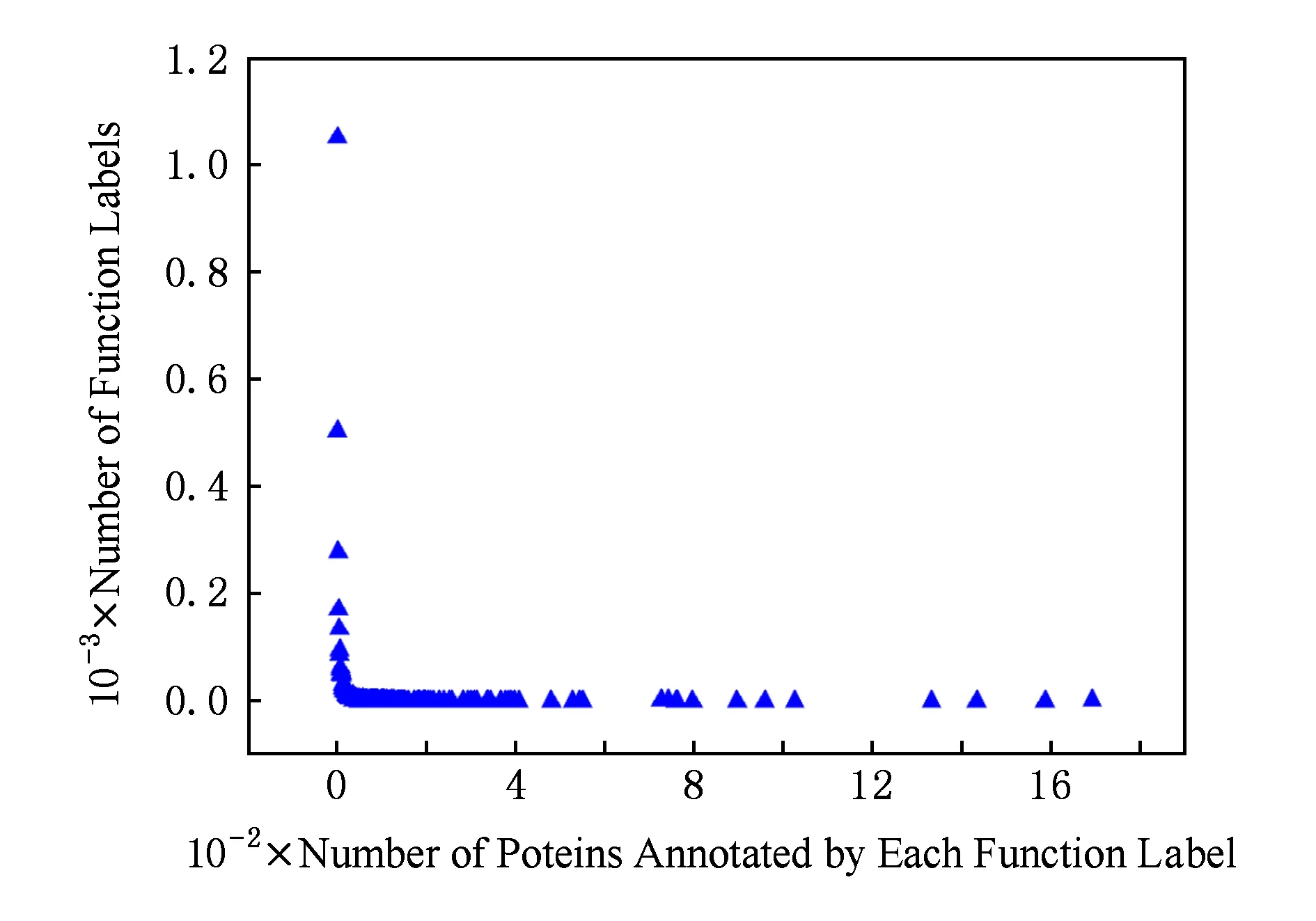
Fig. 1 The number statistics of function labels annotated protein in protein function annotation dataset图1 蛋白质功能注释数据集中标签注释样本频率示意图

面对蛋白质功能标签数据的这一特点，目前蛋白质功能预测方法的研究是采取一种只对低维标签空间分类的策略.这些研究通过一定的规则首先从标签集中选择出一个小规模的标签子集，然后算法仅针对小规模性的标签子集进行训练和预测，而并不是直接面对高维标签空间进行分类.如Yu等人[6]使用文献[12]中的标准蛋白质数据集，这一数据集是通过GO进行生物功能注释，研究者对其中的酵母数据过滤出注释了至少100个蛋白质且最多300个蛋白质的GO功能标签，对人类和小鼠数据过滤出注释了至少30个蛋白质且最多100个蛋白质的GO功能标签.最后，酵母数据中保留的功能标签数量为57个，人类数据保留了254个功能标签，小鼠数据保留了239个标签，继而预测模型只对这些少量的标签进行处理.Xiong等人[13]使用有益功能类[14]的概念来选择GO标签，一个有益GO标签是指：1)至少注释了30个蛋白质；2)没有任何孩子标签注释至少30个蛋白质.最后，该研究在酵母数据集中获得了66个有益的GO标签，并且在小鼠注释数据集中获得了130个有益GO term，同样预测模型也仅对有益GO标签进行预测.显然，以上这些方式可以大大减少分类器所面对的标签数量，但同时预测结果也仅限于小规模的标签子集内.因此，目前蛋白质功能预测方法的研究其实并没有真正解决大量标签分类问题.

基于以上考虑，本文针对蛋白质功能注释标签数量庞大的问题，提出一种基于布尔矩阵分解的蛋白质功能预测框架(protein function prediction based on Boolean matrix decomposition, PFP-BMD)，并特别针对框架中的精确布尔矩阵分解(Boolean matrix decomposition, BMD)模块进行具体研究，提出一种基于标签簇的精确BMD算法Label-Cluster.本文的研究也是首次基于布尔矩阵分解针对蛋白质功能预测问题开展的研究，可为各种多标签分类器在蛋白质功能预测中的高效应用奠定基础.

1 相关工作

除了在蛋白质功能注释数据中，在文本和图片分类场景中也会存在标签数量过于庞大的问题.针对这一问题，一种称为标签空间降维(label space dimension reduction, LSDR)的方法被研究者们提出，其基本思想就是利用矩阵降维技术将标签空间矩阵投影到低维标签空间，多标签分类器的训练和测试都只对低维标签空间进行.

Hsu等人[15]在2009年利用压缩感知技术首次实现了该类方法.此后研究者们相继利用主成分分析[16]、典型相关分析[17]和奇异值分解[18]等手段对LSDR进行了研究.尽管主成分分析和奇异值分解等矩阵降维技术可以很好地将大规模标签降维一个低维空间，但是降维后的空间也失去了原始标签的含义.为了解决这一问题，Balasubramanian等人[19]提出了标签子集选择的思想，即低维标签选择自原标签空间.此后，Bi等人[20]提出了多标签分类的列子集选择方法(column subset selection for multi-label, CSS-ML)，该方法基于一个随机采样过程选择出k个标签以尽可能覆盖所有的标签，并且在选择好的标签上学习了k个分类器.总的来说，以上方法都只是将标签矩阵看作一个普通的矩阵来进行维度降低.从多标签分类的角度看，蛋白质功能标签矩阵显然是一个布尔矩阵(只有2种值0和1).文献[21]已证明：某些能够进行精确BMD的矩阵却不一定能进行普通的矩阵分解，因此BMD对标签的降维效果要好于普通矩阵分解.

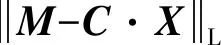
通过以上分析可知，数量庞大的蛋白质功能注释标签已成为提高各类多标签分类器预测效果的一大障碍.本文采用BMD方法实现蛋白质功能预测过程中功能标签的维度降低，即可保留功能标签的生物意义亦可完成更精确的降维.同时，本文在PFP-BMD中使用精确BMD算法，能够使降维后的分类及还原最大程度地保留分类器的分类精度，而“列利用条件”则可使降维后的标签空间仍然具有原标签的意义.

2 基于布尔矩阵分解的蛋白质功能预测框架

在本节中，我们详细介绍PFP-BMD的基本思想.

2.1 蛋白质功能预测及相关符号定义

基于多标签分类的思想，本文首先对蛋白质功能预测问题进行形式化定义：

蛋白质功能预测的任务就是从已知特征向量和功能标签向量的训练数据集Dtrain={X1,X2,…,Xm|Xd=(Fd,Yd),d∈[1,m]}中，对多标签分类模型进行训练，然后使用训练好的模型对已知特征向量但未知功能注释标签向量的新蛋白质Dtest={X1,X2,…,Xn|Xd=(Fd,?),d∈[1,n]}，预测出其功能标签Yd.

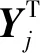
2.2 框架描述

Fig. 2 The framework of protein function prediction based on Boolean matrix decomposition图2 基于布尔矩阵的蛋白质功能预测框架

为了解决蛋白质功能预测中数量庞大的功能标签问题，本文采用LSDR的思想，在预测过程中加入精确布尔矩阵模块以实现蛋白质功能标签矩阵的降维和还原，精确BMD模块与多标签分类器一起构成了本文的PFP-BMD.PFP-BMD的流程描述如图 2所示:

PFP-BMD的基本思想为：

由图2可看出，基于布尔矩阵分解的蛋白质功能预测框架的优势在于：利用精确的布尔矩阵分解得到的矩阵能够一定程度上减轻多标签分类器的训练及预测任务，而多标签分类器的输出结果只需要和矩阵B进行简单的布尔乘即可还原回原标签空间.在框架中，精确BMD模块和多标签分类器模块是2个相对独立的部件，因此该框架可适用于多种多标签分类器，其中精确BMD模块既能保留在分类时标签的生物意义，同时在还原回原标签时并不降低分类精度.

3 精确布尔矩阵分解算法

在本节中，我们针对PFP-BMD中的精确BMD模块进行具体研究，提出一个改进的精确布尔矩阵分解算法Label-Cluster.

3.1 精确布尔矩阵分解算法基础

本节首先给出布尔矩阵分解的定义及文献[27]中的相关定义、命题和定理.

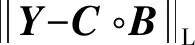
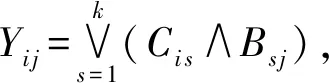
换句话说，布尔矩阵乘法就是在普通矩阵乘法中加一条额外的定义1+1=1，最小的k通常被称为Y的布尔轶，且已有研究表明一个布尔矩阵的布尔轶可能大于或小于它的实数轶[28].对于可以找到最小k的布尔矩阵分解算法，则称其为最优布尔矩阵分解.

即Y=C∘B.

定义1.给定2个布尔矩阵U=(Ui j)∈{0,1}m×n和V=(Vi j)∈{0,1}m×n，如果对于所有的i=1,2,…,m和j=1,2,…,n都满足Ui j≥Vi j，则称U≥V.

命题1.布尔乘法满足扩展:

在文献[27]所提出的BMD方法中，首先证明了存在一个布尔矩阵J，使得Y=Y∘JT成立，并且当J中的任意元素从0改变为1时等式就不再成立，即J是使等式成立的最大矩阵.文献中所提出的启发式算法Remove-Smallest基于2个定理：

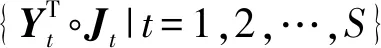
3.2 功能标签关联矩阵

矩阵J在文献[27]中与原矩阵Y一起构成了最优布尔矩阵分解的搜索空间.在对矩阵J的深入研究中，本文发现：矩阵J本质上是对原矩阵Y各列关联关系的一种表示.我们将在本节对蛋白质功能预测中的功能标签关联矩阵A进行定义，以及通过推论1证明其与矩阵J的关系.

在蛋白质功能注释命名方案GO和FunCat中，蛋白质的功能标签之间具有层次关系，FunCat中是树形结构，而GO中是有向无环图(directed acyclic graph, DAG)结构.也就是说，不论是在FunCat还是在GO中，用于蛋白质功能预测的多标签分类器必须满足层次约束，即被一些功能注释的蛋白质一定会被这些功能的父节点功能注释.本文使用符号parent(ci)表示功能标签ci的父标签集，使用des(ci)表示功能标签ci的祖先标签集.如图3所示c1到c8共8个功能标签的层次关联，其中des(c7)={c1,c2,c3,c4}.

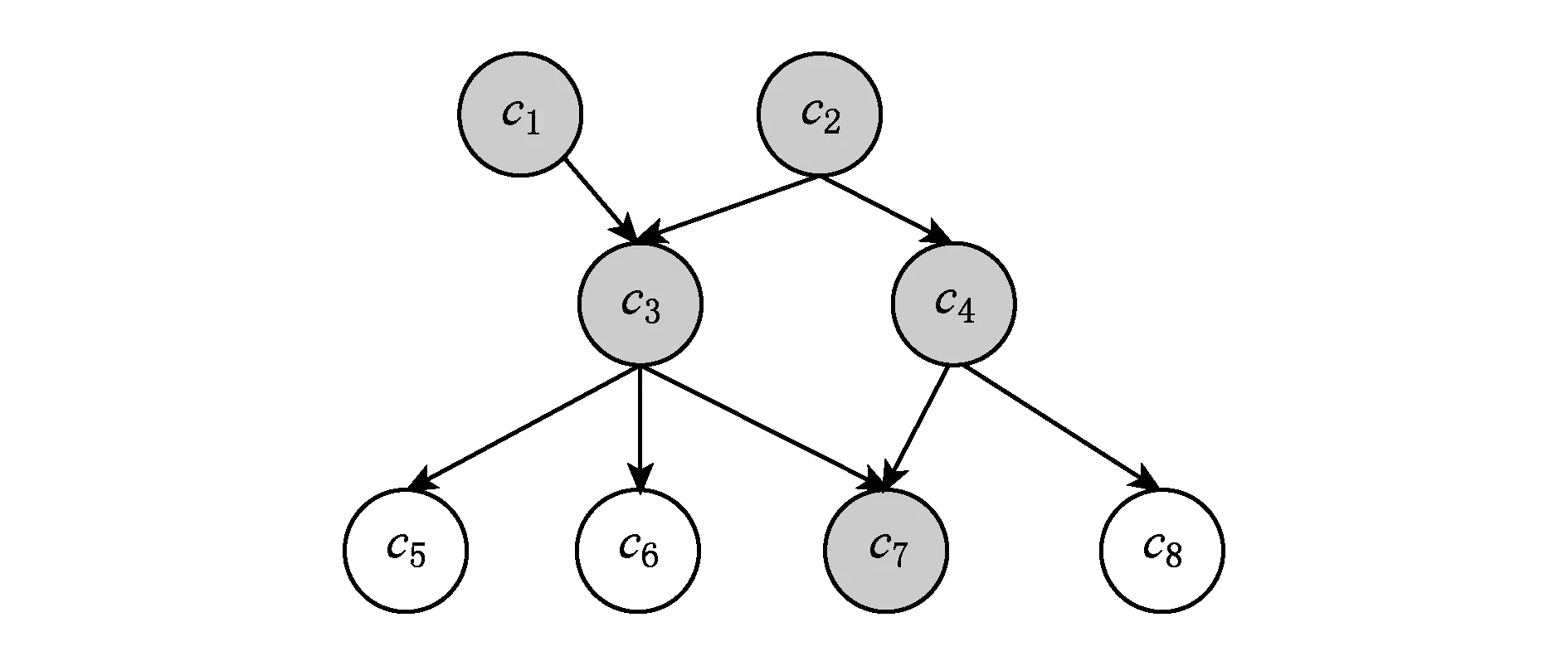
Fig. 3 The diagram of associated labels图3 标签关联示意图

对于功能标签间的DAG层次关联关系，本文使用了一个矩阵A=(Ai j)∈{0,1}S×S来描述，A中的元素Ai j满足：若功能标签ci∈des(cj)则Ai j=1，否则为0.显然，矩阵A可通过功能标签间固有的DAG关系计算得出图3的矩阵A：

下面通过推论1来证明矩阵A和矩阵J之间的关系.

证明. 从定理1可得只要证明Y=Y∘AT，则有J≥A.在A中，Ai j=1表示第i个标签是第j个标签的祖先；在AT中，(AT)i j=1说明第i个标签是第j个标签的子孙；显然对于A和AT，Ai i=1以及(AT)j j=1成立.下面分2种情况进行证明：当矩阵Y中的元素Yi j=1时，由于有(AT)j j=1，则Y∘AT中的元素(Y∘AT)i j=1；当矩阵Y中的元素Yi j=0时，由于矩阵Y中的第i行不可能存在一个元素Yi k=1且AT中的(AT)k j=1，因为(AT)k j=1说明标签k是标签j的子孙，如果Yi k=1则一定有Yi j=1，这与假设相背，因此Y∘AT中的元素(Y∘AT)i j=0.综上2种情况，Y=Y∘AT均成立，则由定理1可得J≥A成立.

证毕.

从推论1可以看出，矩阵J不仅覆盖了原始标签集的一个DAG关联，并且还反映了由矩阵Y中的值隐含的列之间的关联关系.因此，矩阵J本质上是一个标签关联矩阵.

3.3 基于标签簇的布尔矩阵分解算法

由3.2节讨论可知，对于矩阵Y，矩阵A反映的是标签间固有的层次约束关系，即Y中的元素必须满足：如果矩阵A中的元素Ai j=1，且Yd j=1，则Yd i=1.换句话说，当子孙标签cj注释了某蛋白质d时，它会使得cj所有的祖先标签des(cj)均注释该蛋白质.如图3中的功能标签c7，其所注释的蛋白质也一定被其祖先标签集des(c7)={c1,c2,c3,c4}所注释.

基于以上这种层次约束关系，如果将矩阵Y中所有祖先标签这种因其子孙扩展而来的注释关系去掉，那么可能会出现大量祖先标签注释蛋白质的数量为0，当将这些不再注释蛋白质的祖先标签从标签集中去掉时，并不会影响其他标签对蛋白质的注释关系，而通过祖先标签与保留的子孙标签的层次关联关系，又可以很容易地恢复祖先标签对蛋白质的标准.显然，只需保留最下层的叶子标签即可最大程度地删除不再注释蛋白质的祖先标签.本文将这种保留下的子孙标签称为一个标签簇，因为尽管保留下来的仅仅是一个单独的子孙标签列，但是它却包含了从它开始向上扩展一直到根标签的一个标签子集.

如图3中的功能标签c7可与其祖先标签集构成一个标签簇{c1,c2,c3,c4,c7}，而c7对蛋白质的注释数据同时也可反映出c1～c4是否注释了某些蛋白质.如果对矩阵Y找出所有这样的标签簇，保留下标签簇中的最下层标签，那么相当于实现了标签空间的降维，而标签簇对蛋白质的注释矩阵与标签簇与标签的对应关系矩阵相乘则可得到对原标签空间的还原，这一过程实际就是一个精确的BMD.

由推论1可知，矩阵J本质上是一个标签的关联矩阵且J≥A，即矩阵J描述功能标签间关联关系最完整的矩阵，不仅包含功能标签间固有的DAG关系，同时还包含了矩阵Y中的值之间反映的关联关系.因此，按照以上标签聚簇思想同样可基于矩阵J来构造标签簇集，以完成Y的精确BMD.基于以上分析，本文提出了基于标签簇的精确BMD算法，如算法1所示:

算法1.Label-Cluster算法.

① 输入布尔矩阵Y∈{0,1}D×S；

③ For eachi=1,2,…,Ddo

For eachj=1,2,…,Sdo

IfYi j=1 then

End If

End For

End For

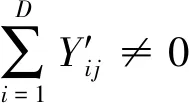
⑤ 计算矩阵B∈{0,1}k×S:从J中挑选出对应到C中的k列得到J′∈{0,1}S×k，最后得到B=(J′)T;

⑥ 对矩阵C按照矩阵B进行标签关联扩展：若对于Ci j=0，存在Ci m=1且Bm j=1，则Ci j=1;

⑦ 输出布尔矩阵C∈{0,1}D×k和B∈{0,1}k×S.

在Label-Cluster算法中，矩阵C成为了蛋白质功能的“标签”矩阵，其中每一个新的功能“标签”(即C中的每一列)既是一个原始标签也代表了原始标签集的一个子集(标签簇：一个原始标签的所有祖先标签及其本身的一个集合)，即满足“列利用条件”约束.对于每个蛋白质，矩阵C以一个更低的维度表现了蛋白质所有的原始功能标签，而矩阵B中的每一行是一个标签簇到原始标签的一个对应关系，如果Bi j=1，那么标签簇i中包含了原始标签j，否则为0.矩阵B所描述的这种标签簇与标签间的对应关系，可以很自然地用于标签簇矩阵到原始标签矩阵的还原.

同时，需要注意的是:不是所有的祖先标签都能在被聚簇后而在矩阵C中被消去，除非它对所有蛋白质的注释都能被其标签簇所表示.因此，在算法1中，步骤2首先是将对矩阵Y中的每一个元素进行更新，如果Yi j=1，且存在j的某孩子标签m有Yi m=1，那么将Yi j更新为0，在对Y中的每个元素进行更新后，如果某标签可以被其标签簇完全表示，那么该列将全部为0，即可删除.在步骤3删除全0列得到矩阵C之后，还需要步骤5对步骤2中更新为0但没有被随列删除的元素进行恢复，进而使得矩阵C满足“列利用条件”.因此算法1是对聚簇操作的一种程序实现的具体表示，与本节所阐述的聚簇思想相对应.

3.4 Label-Cluster算法的相关推论及证明

为了证明Label-Cluster算法可得到矩阵Y的最优精确布尔矩阵分解，我们在本节中通过4个推论对其进行证明.

推论2.给定一个布尔矩阵Y∈{0,1}D×S，(C,B)=Label_Cluster(Y)，C∈{0,1}D×k且B∈{0,1}k×S.那么通过算法Label-Cluster′(将Label-Cluster中的矩阵J替换为任意满足式Y=Y∘HT的矩阵H)可得到(C′,B′)=Label_Cluster′(Y)，C′∈{0,1}D×k′且B∈{0,1}k′×S，则k≤k′成立.

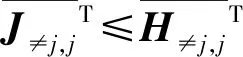
证毕.

通过推论2可得，在算法Label-Cluster中基于矩阵J所得到的矩阵C的列数k是最小的，若在Label-Cluster算法中基于其他关联标签关联矩阵所得到的矩阵C的列数k′均大于k.

推论3.给定一个布尔矩阵Y∈{0,1}D×S，(C,B)=Label_Cluster(Y)，C∈{0,1}D×k且B∈{0,1}k×S，则Y=C∘B成立.

证明. 假定Yi j=0，当C中第i行的任意元素Ci m=1，说明第i个实例被第m个标签簇所标注，如果有Bm j=1，说明第m个标签簇包含了第j个标签，则第i个实例一定也被第j个标签所标注，即Yi j=1，但这与假设相悖.因此当Ci m=1时，一定不存在Bm j=1，则(C∘B)i j=0.假定Yi j=1，因为C中不存在全0列，因此一定有一个Ci m=1，同样，如果Bm j=0，说明第m个标签簇不包含第j个标签，那么第i个实例一定不被第j个标签所标注，即Yi j=0，这与假设相悖.因此当Ci m=1时，一定有Bm j=1，则(C∘B)i j=1.综上所述，2种情况下Yi j=(C∘B)i j，即Y=C∘B成立.

证毕.

通过推论3可得，算法Label-Cluster所得到的矩阵C和B是Y的精确BMD.

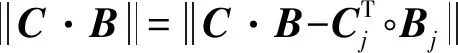
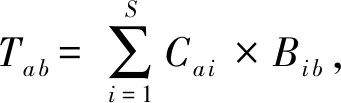
证毕.

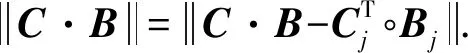
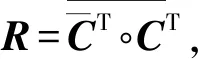
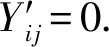
证毕.

由推论4和推论5可得，算法Label-Cluster得到的矩阵C和B满足：如果再从矩阵C和B中删除列和行，则所得到的矩阵不再能满足Y的精确分解.即证明了矩阵C和B是Y的最优布尔矩阵分解.

4 蛋白质功能预测实验

在本节中，我们分别对Label-Cluster算法和PFP-BMD在3个数据集进行了实验验证，并选用针对大规模标签的分类模型与本文所提方法进行对比.

4.1 数据集

为验证Label-Cluster算法和PFP-BMD的有效性及优势，本文采用了一个被广泛使用的标准蛋白质功能预测数据集酵母数据集(s.cerevisiae dataset, S.C)[9]进行实验分析.该数据集的蛋白质特征数据包含酵母基因的多个方面，如序列统计特征、表型特征、基因表达特征、二级结构特征和同源特征等，其包含了S.C-1到 S.C-12共12个数据集，并且每个数据集都使用了FunCat和GO这2种功能注释方案，本文主要使用了S.C中GO功能注释方案的S.C-1到S.C-3数据集.该数据集的数据格式都是Weka(waikato environment for knowledge analysis)的arff文件，以便于更多的Weka中的基准多标签分类算法应用到该数据集上.由于S.C数据集均已根据GO功能标签间的DAG结构对标签注释数据进行了扩展，因此本文无需再做此预处理.

Table 1 The Statistics of S.C Dataset表1 S.C数据集统计

4.2 Label-Cluster实验分析

4.2.1 对比算法及时间复杂度分析

本节将Label-Cluster算法与文献[27]中的Remove-Smallest算法进行蛋白质功能标签矩阵降维实验对比.由于Remove-Smallest和Label-Cluster算法都是属于精确BMD方法，均能完整地还原回原矩阵空间，因此2个算法在文献[27]中使用的BMD算法评价标准覆盖率值均为100%.下面对2个算法的时间复杂度进行分析.

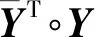
4.2.2 实验结果

Label-Cluster算法分别在上述3个数据集中进行布尔矩阵分解，实验结果如图4所示，图4中降维率=(原标签数量-降维后的标签数量)原标签数量，降维率可以反映了精确BMD算法对不同数据集的降维效果差异，其值越大说明对高维标签的降维程度越高.

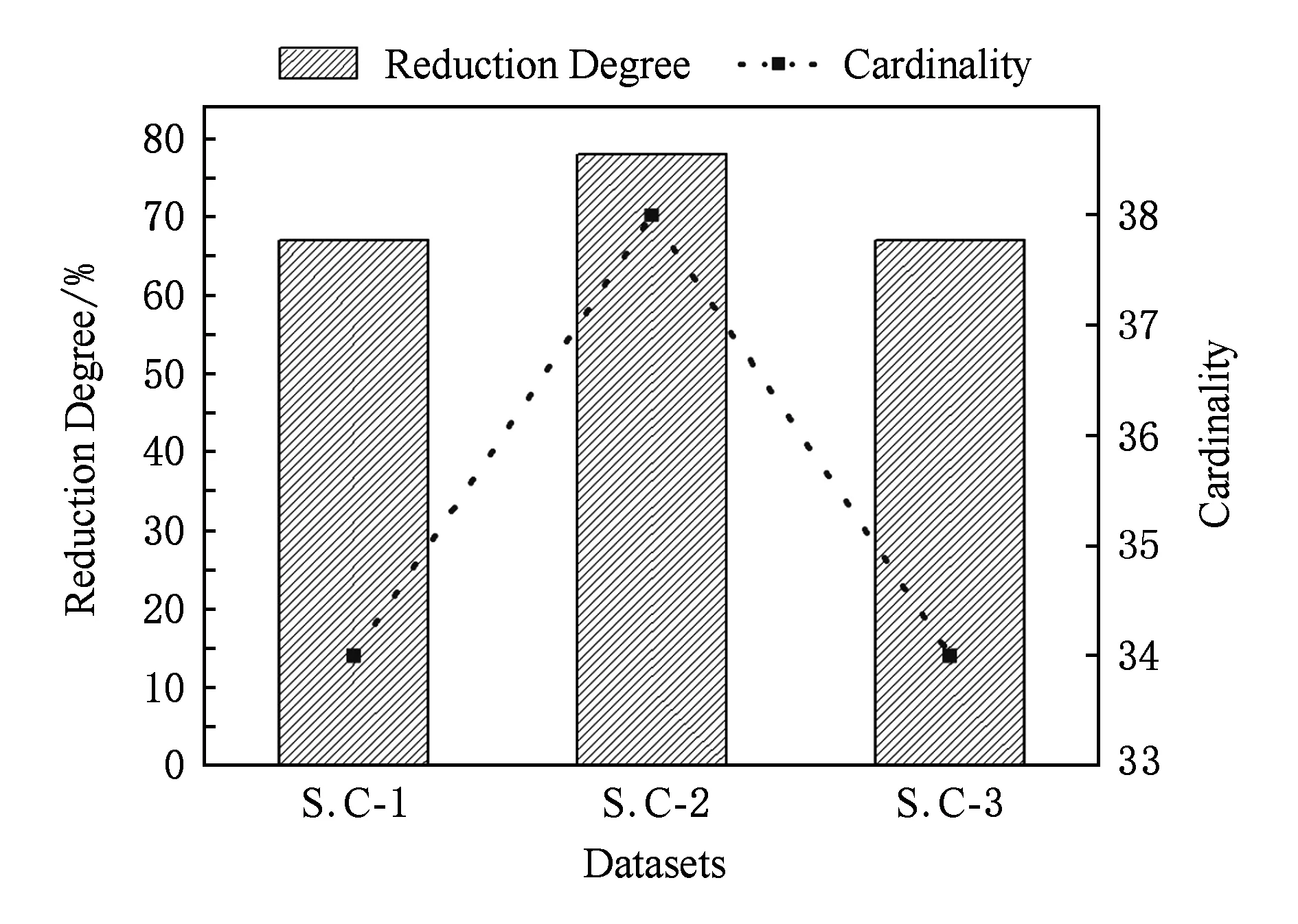
Fig. 4 The dimension deduction comparisons of Label-Cluster algorithm in three dataset图4 Label-Cluster算法在3个数据集上的降维效果对比

由图4可以看出，对于不同的数据集，Label-Cluster算法的降维率不尽相同，其中对S.C-2数据集的降维程度最高.这主要是各数据集中标签的关联程度不同导致的，如图4中的虚线所示，S.C-2数据集的样本平均标签数量要高于S.C-1和S.C-3数据集.换句话说，Label-Cluster算法对于标签关联度更大的数据趋向于得到更高的降维率.

由于Remove-Smallest和Label-Cluster算法都是属于精确BMD算法，因此在不同的数据集上在降维效果上是完全相同的.但由4.2.1节的分析可知，Label-Cluster较Remove-Smallest算法在时间复杂度上有较大优势，表2和图5展示了2个算法运行的实验环境及在不同数据集中的运行时间对比.

Table 2 The Experimental Environment表2 实验环境

从图5可知：本文提出的Label-Cluster相比Remove-Smallest算法在计算速度上有较大提高，运行时间能减少90%左右，且能完成标签矩阵的精确布尔分解，并遵循“列利用条件”.特别是算法中引入了标签簇的思想，对分解后的保留的标签看作是原有标签的一个聚类，更利于解释后续分类的结果.

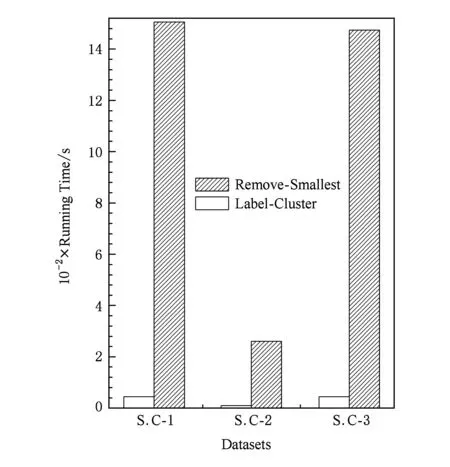
Fig. 5 The run time comparisons of Label-Cluster and Remove-Smallest algorithm图5 Remove-Smallest算法和Label-Cluster算法运行时间对比

4.3 PFP-BMD实验分析

4.3.1 评价标准

蛋白质功能预测作为一个多标签分类问题，可以使用通用的多标签分类评价指标对模型的分类性能进行评估.如引言所述，目前常用的蛋白质功能预测算法主要是针对小规模的功能标签子集进行训练和预测.文献[9]是一个针对大规模蛋白质功能标签集的多标签分类方法研究，为了与此类方法进行对比，本文亦采用了相同的评价标准，即精确率-召回率曲线下面积(area under the precision-recall curve, AUPRC).AUPRC的值越接近于1，则模型性能越好.

在蛋白质功能预测数据集中大部分的功能标签注释的蛋白质数量很少，这也就意味着对于大部分功能标签来说负例的数量会大大超过正例的数量.而本文更加关心的是正确预测出的正例(蛋白质被某个功能标签所注释)，而不是正确预测出负例(蛋白质不被某个功能标签所注释).据此，本文采用PR(precision-recall)曲线进行评价是合理的.

当然，PR曲线仅仅是针对单个的标签来计算，而对于蛋白质功能预测则要同时面对多个功能标签.因此，为了评价蛋白质功能预测方法的整体性能，文献[9]采用了2种AUPRC评价指标.

1) 平均PR曲线下的面积(area under the average PR curve,RMicroAUPRC)

第1种获得多标签分类模型整体性能分数的方法就是通过将多标签分类问题转化为一个二值问题以构造出整体的PR曲线.假设一个二值分类器的输入是一个(样本，类别)对，输出是预测出该样本是否输入该类别，一个排序分类器可以通过选择一个阈值而转化为一个二值分类器，并且通过变化阈值则可得到一条PR曲线.

对于给定的阈值，对应的是PR空间中的一个点的坐标值为(prec,rec)，其定义为

其中，i表示第i个标签，通过变化阈值就可以得到1根平均PR曲线，并将其曲线下的面积表示为RMicroAUPRC.

2) PR曲线下的平均面积(average area under the PR curves,RMacroAUPRC)

第2类方法是求单根PR曲线(一个标签)下面积的权值平均，计算方法如下：

其中，Ri表示第i个标签的AUPRC值.当将所有wi设置为1时，计算结果表示为RMacroAUPRC. 若对wi以不同的策略取值，计算结果表示为RMacroWAUPRC. 在RMacroWAUPRC的计算过程中，对于权值wi最直观的想法就是设置为1|S|，其中S是标签的数量.对于权值wi第2种最自然的取值就是其中vi表示类别si在数据集中出现的频率.第2种权值设置方法反映出标注样本越多的标签越重要.

总的来说，上述2种针对多标签分类的AUPRC值计算方法，RMicroAUPRC实际是对AUPRC值求微平均，因此可称其为PR曲线下面积微平均值(micro average of AUPRC,MICRO-AUPRC)，换句话说RMicroAUPRC是在所有标签的混合中来评价模型.而RMacroAUPRC实际是对AUPRC求宏平均，可称其为PR曲线下面积宏平均值(macro average of AUPRC,MACRO-AUPRC)，RMacroWAUPRC则称为PR曲线下面积带权重宏平均值(macro average of AUPRC with weight,MACRO-WAUPRC)，它们可在一定程度上反映出各个独立标签的预测准确率.

4.3.2 对比算法及实验设置

本节在蛋白质功能预测框架PFP-BMD中的精确BMD模块采用Label-Cluster算法，多标签分类器模块采用多标签最近邻算法(multi-label K-nearest neighbor, MLKNN)[29-30].对比算法使用文献[26]中的MLC-BMAD(multi-label classification using Boolean matrix decomposition)，以及文献[9]中的3个层次多标签分类算法CLUS-HMC，CLUS-SC，CLUS-HSC.

MLKNN是对传统K近邻算法在多标签分类中的一种改进，本文在实验中设置MLKNN的邻居数目为10，平滑因子为1.

MLC-BMAD是一个专门针对大规模标签的多标签分类的方法.其思想与PFP-BMD非常类似，也是先通过BMD对原标签进行降维，预测之后再还原回原标签空间，但MLC-BMaD中使用的是近似BMD算法，因此需预先设定降维后的标签数量，同时本文将MLC-BMAD在3个数据集上的标签关联阈值均设置为0.5.

CLUS-HMC，CLUS-SC，CLUS-HSC是3个基于决策树的层次多标签分类器，其中CLUS-HMC可同时学习所有的层次标签，CLUS-SC是为每个标签学习一棵独立的决策树，CLUS-HSC在CLUS-SC的基础上考虑了标签间的层次依赖.这一个算法在多篇对蛋白质功能预测的研究论文中被证明是一类性能较佳的算法，特别是CLUS-HMC在数据集S.C中的实验结果均优于多个层次多标签分类器及CLUS-SC和CLUS-HSC.本文CLUS-HMCHSCSC算法的实验结果来自于文献[9]中.在文献[9]的实验中，CLUS-HMCHSCSC算法是在完整的S.C数据集中进行，保留了功能标签间的层次关系，且无需经过标签降维.尽管PFP-BMD需要经过标签降维，但降维后的标签还能还原回原始标签，因此它和CLUS-HMCHSCSC算法在预测结果的标签空间上是相同的.

本文的多标签分类实验采用十折交叉验证，实验评价指标使用了4.3.1节所述的RMicroAUPRC，RMacroAUPRC，RMacroWAUPRC3种PRC曲线下面积，对于这3种评价标准，评价标准的值越大，预测准确率越高.

4.3.3 PFP-BMD与MLC-BMAD对比实验结果

由于MLC-BMAD采用的是近似布尔矩阵分解算法进行降维，因此本文分别在3个数据集中为其设置一个降维标签数量的范围，最后与PFP-BMD在固定的降维标签数下进行对比.图 6展示了对比结果:

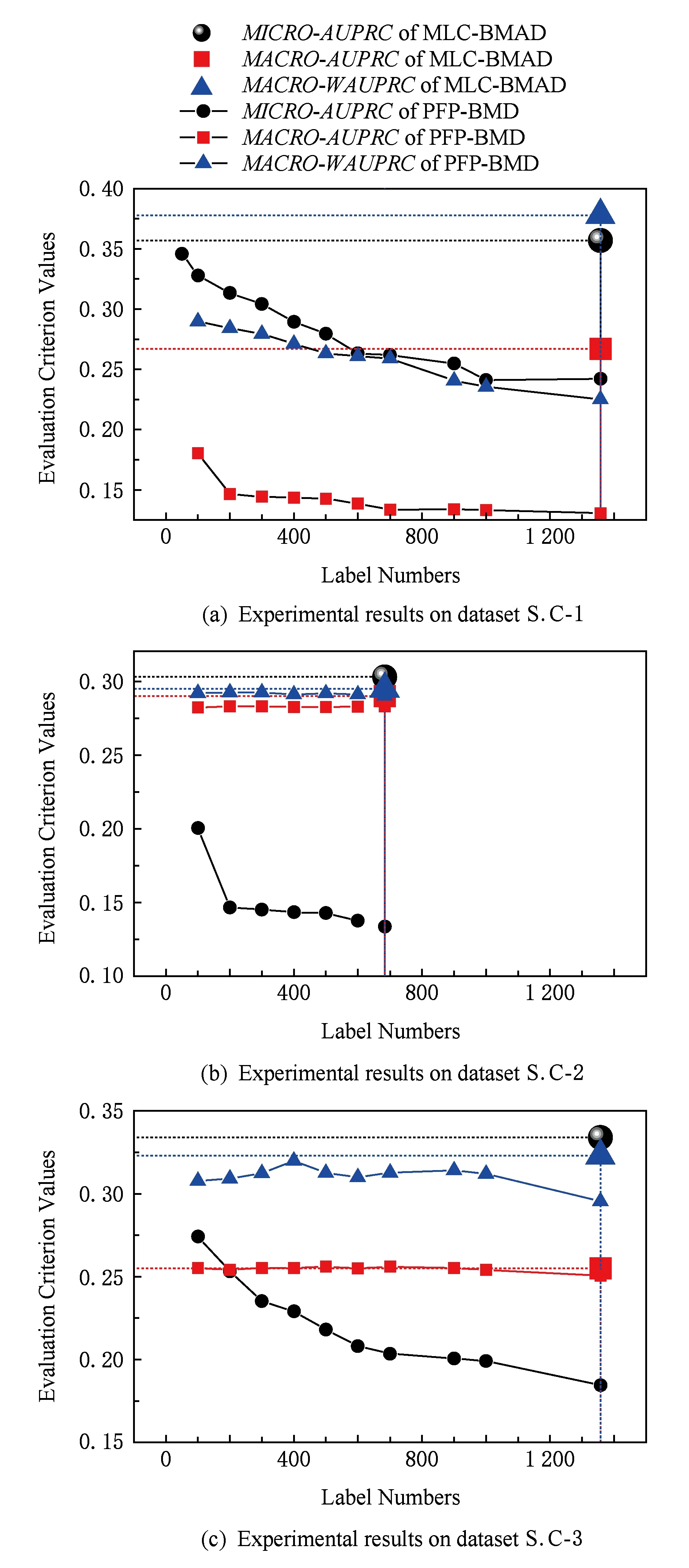
Fig. 6 The experimental comparisons of PFP-BMD and MLC-BMAD图 6 PFP-BMD与MLC-BMAD实验结果对比

由图6可以看出，随着设置的标签数量的增加，MLC-BMAD的3个评价标准值均在降低，这是由于较小的降维后标签数量可使分类器获得更高的分类准确率.同时，由于MLC-BMAD所使用的近似布尔矩阵分解算法不能够在分类后将标签矩阵精确还原，这会大大损失还原后的分类准确率.因此对于S.C-1，S.C-2，S.C-3数据集，尽管MLC-BMAD方法可设置较大范围的降维后标签数量，但与PFP-BMD固定数量的降维标签相比，MLC-BMAD在3个评价标准RMicroAUPRC，RMacroAUPRC，RMacroWAUPRC上所获得的值显著低于PFP-BMD.在数据集S.C-1上，PFP-BMD的RMacroWAUPRC值高于MLC- BMAD在各降维标签数量范围内平均值的31%，RMacroAUPRC值高于MLC-BMAD的46%，RMicroAUPRC值高于MLC-BMAD的20.4%；在数据集S.C-2上，PFP-BMD的RMacroWAUPRC值高于MLC-BMAD在各降维标签数量范围内平均值的1.2%，RMacroAUPRC值高于MLC-BMAD的2.5%，RMicroAUPRC值高于MLC- BMAD的50%；在数据集S.C-3上，PFP-BMD的RMacroWAUPRC值高于MLC-BMAD在各降维标签数量范围内平均值的4%，RMacroAUPRC值高于MLC-BMAD的0.1%，RMicroAUPRC值高于MLC-BMAD的34%.

由图7所示，在将所有标签看作同等重要的评价指标RMacroAUPRC上，PFP-BMD具有显著优势.分别与CLUS-HMC，CLUS-HSC，CLUS-SC相比：PFP-BMD在数据集S.C-1上的RMacroAUPRC值提高了86.5%，86.9%，86.9%；在数据集S.C-2上的RMacroAUPRC值提高了92.7%，93.4%，92.7%；在数据集S.C-3上的RMacroAUPRC值提高了90.2%，90%，90%.这是由于RMacroAUPRC的计算并不偏重于反映注释较多蛋白质的功能标签预测准确率，而是针对所有标签预测准确性的平均.在PFP-BMD中，注释蛋白质较少的功能标签在BMD之后更趋向于被降维删除，但矩阵B表示了它和保留标签的关联关系，可以通过矩阵还原较准确的得到它的预测结果，以此提高了所有标签的平均预测准确率.同时，由图7也可以看出，CLUS-HMC，CLUS-HS，CLUS-SC这3个算法在数据集S.C-1到S.C-3上获得了相似的RMacroAUPRC值.PFP-BMD在RMacroAUPRC上的优势说明PFP-BMD较CLUS-HMCHSCSC更有利于提高标注蛋白质少的标签的分类结果.

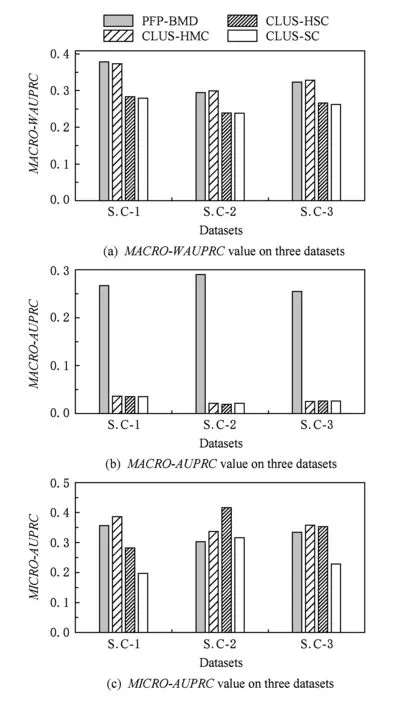
Fig. 7 The experimental comparisons of PFP-BMD and CLUS-HMCHSCSC图7 PFP-BMD与CLUS-HMCHSCSC实验结果对比

同时，对于考虑了标签标注频率的评价指标RMicroAUPRC，PFP-BMD在3个数据集上的值略低于CLUS-HMC，但在RMacroWAUPRC评价标准上获得了和CLUS-HMC基本一致的结果，且显著优于CLUS-HSC和CLUS-SC.在数据集S.C-1上，PFP-BMD的RMacroWAUPRC值和CLUS-HMC相比提高了1.3%，和 CLUS-HSC相比提高了25%，和CLUS-SC相比提高了26%；在数据集S.C-2上，PFP-BMD的RMacroWAUPRC值和CLUS-HMC相比降低了1.3%，和CLUS-HSC相比提高了19%，和CLUS-SC相比提高了19%；在数据集S.C-3上，PFP-BMD的RMacroWAUPRC值和CLUS-HMC相比降低了1.5%，而和CLUS-HSC相比提高了17.6%，和CLUS-SC相比提高了 18.9%.CLUS-HMC在考虑了标签标注频率评价标准上的优势是由于这类层次多标签分类算法在分类过程中考虑了标签间的层次关系，因此对于处于底层的标注频率较高的标签具有更好的预测准确率，而标注频率较高的标签预测结果对RMicroAUPRC和RMacroWAUPRC的贡献较大.

总结：从以上实验结果可以看出，本文PFP-BMD的首先利用Label-Cluster算法完成对蛋白质功能标签矩阵的精确布尔矩阵分解，能有效地降低后续多标签分类器的负担并提高多标签分类器的分类准确率，最后再通过Label-Cluster算法得到的矩阵B可完整地将预测结果还原回原标签空间.这类LSDR的思想与直接对大规模功能标签进行分类的方法相比(如CLUS-HMCHSCSC)，由于在降维过程中趋向于舍去标注蛋白质少的功能标签，但最后在还原过程可以对其进行完整的还原，因此对于提高这一类功能标签的预测准确率具有明显优势.而与近似布尔矩阵分解的多标签分类方法相比(如MLC-BMAD)，尽管近似布尔矩阵可以任意指定降维数以获得更低的标签维数，但近似还原同时也会一定程度地降低功能标签的预测准确率，而Label-Cluster算法可以在不降低预测准确率的条件下对标签矩阵进行精确还原，因此本文提出的方法在与MLC-BMAD的对比实验中仍取得了较好的结果.

5 结束语

蛋白质功能注释是蛋白质组学最重要的研究内容，通过各种可计算模型实现蛋白质功能的自动注释是当前生物信息学的一个研究热点.本文将蛋白质功能预测作为一个多标签分类问题进行研究，针对蛋白质功能标签数量庞大的问题，提出了一种基于布尔矩阵分解的蛋白质功能预测框架.并针对框架中的布尔矩阵分解模块，提出了一种基于标签簇的精确布尔矩阵分解算法Label-Cluster.该算法利用标签关联矩阵J对标签矩阵进行标签簇构造，每一个标签簇代表了一个原始标签的所有祖先标签及其本身的集合，因此满足“列利用条件”约束.实验结果表明：Label-Cluster算法能够有效地完成大规模标签降维任务并且在运行速度上具有明显优势，且应用该算法的蛋白质功能与PFP-BMD能够有效提高大规模功能标签的整体预测准确率，特别对于提高注释蛋白质数量较少的功能标签预测准确率具有较大优势.

同时，PFP-BMD中多标签分类器的选用对分类结果有较大影响，尽管本文的实验部分仅选用了MLKNN一种分类器，但PFP-BMD可支持多种分类器的应用，因此PFP-BMD的实验效果还具有较大的提升潜力.目前，随着网络应用的蓬勃发展，使得更多的多标签分类场景中的实例倾向于与大量的标签相关联，而本文所提出的PFP-BMD和Label-Cluster算法将蛋白质功能预测的过程作为一种通用的多标签分类场景进行处理，因此本文的研究对于各领域中的大规模多标签分类问题也具有广泛的应用价值.