基于自适应人工鱼群FCM的异常检测算法
2019-05-15张凤斌
席 亮 王 勇 张凤斌
(哈尔滨理工大学计算机科学与技术学院 哈尔滨 150080)
异常检测(anomaly detection)在电信、保险、银行、灾害气象预报、医疗领域等多个领域得到了广泛应用,特别在计算机图形图像、网络安全等研究领域,基于数据挖掘、机器学习等智能技术的异常检测研究表现得尤为活跃[1].基于机器学习的异常检测方法需要收集大量样本,特别是异常样本.然后,基于这些异常样本,通过某种智能学习方法或模型进行规则集的训练,最后使用训练后的规则集进行异常分析与检测[2],是本领域的一个研究热点.
聚类分析是机器学习经常采用的经典方法之一.其基本思路是根据数据样本间存在的某种隐形关系进行分析,然后将这些样本划分为不同的簇.这一显著特点非常适合用于检测异常特征[3].其中,模糊C-均值聚类算法(fuzzy C-means, FCM)是无监督机器学习算法中非常经典的算法之一.其最显著特点是不需要事先标记数据记录的类别信息[4],在异常检测领域得到了广泛应用[5].然而,FCM对初始值依赖程度较高,容易陷入局部极小值,而且,通常需要较多的迭代次数[6].为此,人们采用了多种优化措施对其进行改善[7],如文献[8]将FCM与遗传算法(genetic algorithm, GA)相结合,提出GA-FCM,该算法首先选择最优个体并对其进行交叉与变异操作,不断迭代产生新的最优个体,直至产生最优的初始聚类中心来改善FCM对初始值依赖程度高、易于收敛于局部最小值的弊端.肖满生等人[9]提出了一种空间相关性的FCM,根据数据集的空间分布特征设计其影响值来改善聚类中心,从而减少对噪声的敏感程度;陈海鹏等人[10]引入软划分方式,采用不同的聚类数来进行多次聚类分析,最后利用寻优求得的有关隶属度信息来构建相关矩阵,以此获得最终结果.以上算法虽然在一定程度上降低了FCM对初始值的依赖程度,但实现起来比较复杂、计算量大,迭代次数会有所增加.

Fig. 1 Basic model of anomaly detection图1 异常检测基本模型
人工鱼群算法(artificial fish-swarm algorithm, AFSA)是模拟鱼群的觅食行为而设计出的一种智能生物寻优算法.它具有较强的鲁棒性,对初始值选取不敏感、计算简单且全局收敛性好.而FCM的目标是优化目标函数取得最优值.因此,将AFSA应用于FCM,可以帮助其解决易陷入局部极值的问题.然而AFSA的迭代次数不易控制的问题也需要引起重视.目前,已有相关文献阐述了AFSA在不同应用背景下的良好效果.如文献[11]将AFSA与SVM(support vector machine)相结合,运用于医疗领域,提高了具有较少特征的特征子集的分类精度,为疾病诊断提供可靠帮助;文献[12]提出了一种基于AFSA优化的特征选择方法,将其应用到大数据处理中,在减少数据库维度的同时获得更好的性能;文献[13]将AFSA算法应用到求解柔性作业车间调度问题中,从而提高其求解性能与收敛速度;文献[14]将AFSA算法应用到无线传感器网络中解决簇头难寻问题,从而提高网络的性能;文献[15]将AFSA算法应用到能源调度中,合理安排能源,实时保持负荷生成平衡.
鉴于此,本文改进AFSA算法,加入自适应机制来控制迭代次数.然后将其运用到基于FCM的异常检测以提升系统的检测性能.其基本过程为:改进AFSA,使其随着算法的不断迭代,自适应改变视野范围,并最终计算出问题最优解;然后将该解作为FCM初始聚类中心进行聚类分析,将正常与异常数据划分为不同簇,从而完成异常分析与检测过程.
1 相关工作
1.1 基于FCM的异常检测算法
异常检测通过实时监视系统中的各类事件,对各类异常行为进行自动识别和检测.其基本模型如图1所示[16];基于FCM的异常检测是融入了聚类的思想,根据正常与异常特征的本质不同,把它们尽量地分为不同的簇且不出现交集的方法[17].
基于FCM的异常检测方法应用很广泛.在医疗领域应用方面,文献[18]将基于FCM的异常检测应用于脑部核磁共振图像分割中,通过FCM算法对强度不均匀性进行校正,从而提高算法对组织分割的精准度;文献[19]将基于FCM的异常检测应用于脑肿瘤分割核磁共振图像,并引入人工蜂群算法,减少噪声的影响,有助于识别脑肿瘤.在电力系统应用方面,文献[20]引入纵横交叉算法优化FCM异常检测算法,有效弥补单一算法的不足,实现了对电力大客户全面与精确地精细化分类;文献[21]将FCM与自适应模糊推理进行结合,提高系统的检测准确率,该模型可迅速检测出配电网的异常情况及故障等级状况.
在基于FCM的异常检测中,经常采用Euclidean距离衡量样本间差异,较适用于对球性结构的数据集进行聚类.当问题空间维度在较高水平时,需要较长时间才可收敛.Mahalanobis距离的计算仅和协方差矩阵的逆有关,它关心样本的数目而非样本的维度.因此,它较适用于对较高维数据向量进行聚类,比基于Euclidean距离的FCM所用的时间短.
1) Mahalanobis距离
设A是一个n×l输入矩阵,其中包含n个样本,A=(ni)(i=1,2,…,n).ni到A的样本均值之间的Mahalanobis距离可定义为

(1)
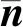
(2)
Xiang等人[22]利用Mahalanobis距离可以自适应地调整数据的集合分布,将其应用到模糊聚类,取得了较好的结果.因此,本文将选用Mahalanobis距离衡量样本间差异.
2) 基于Mahalanobis距离的FCM算法
其目标函数可表示为
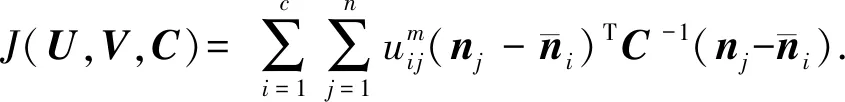
(3)
其中,U为隶属度矩阵,V为聚类中心矩阵.基于Mahalanobis距离的FCM算法的目标是使该式获得最小值.其约束条件:
(4)
为隶属度.然后使用Lagrange乘子法可得:
(5)
(6)

(7)
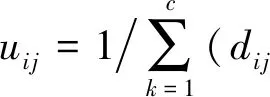
(8)
其中,1≤i≤c,1≤j≤n,c为划分簇类中心的数量.
基于Mahalanobis距离的FCM算法需要3个参数:c、迭代终止误差ε和模糊加权指数m.其中,c是预先给定的,根据文献[23]得到m的最优取值区间为[1.5,2.5],一般取其区间中值,ε通常可取10-5.算法实现:
Step1. 给定c,m,ε,初始迭代f的值等于0,U使用[0,1]间的随机数进行初始化,使其满足式(4)的约束条件;
Step2. 根据式(6)计算c个聚类中心Vk;
Step3. 根据式(8)计算本次迭代的U(f),并根据式(3)计算本次迭代中的J(f);
Step4. 如果|J(f)-J(f-1)|≤ε条件成立,则输出结果,否则f=f+1,转Step2执行.
3) 算法分析
① 初始化U的时间复杂度为O(cn),初始化其他参数的时间复杂度为O(1).
② 计算c个聚类中心,其时间复杂度为O(nlc).
③ 计算目标函数,时间复杂度为O(nlc).
④ 算法共迭代f次,因此,本算法总的时间复杂度为O(nlcf).
1.2 人工鱼群算法
人工鱼群算法是根据鱼的自由游动特征提出的一种智能全局寻优算法.鱼聚集的越多则该区域的食物越丰硕.根据该特点,构造人工鱼,模仿鱼群在自然环境下捕食、群居、追逐等行为[24].每条人工鱼代表问题的一个解,问题的解空间对应着人工鱼的生活水域,所求的目标函数的值对应着食物浓度,算法通过在求解空间中的不断迭代计算来搜寻问题的最优解.AFSA主要包括4个步骤:


(9)

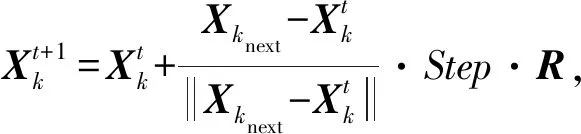
(10)
其中,Step为移动步长.反之,按照式(11)选择另一位置,判断是否前进.如果在尝试一定次数后仍无法满足前进条件,则执行步骤4.

(11)
2) 聚群行为.设第k条人工鱼的状态为Xk,寻找其Visual范围内同伴的数量.设同伴数量为num,人工鱼规模为N,如果numN<δ,(0<δ<1),则说明同伴周围的营养丰富且鱼群数量适当.其中δ为拥挤度因子.如果同时满足Yk>Yc,则向中心位置Xc移动1步:

(12)
否则,执行步骤1.
3) 追尾行为.设第k条人工鱼的位置为Xk,寻找其Visual范围内状态最佳的同伴Xmax.如果Yk>Ymax,且Xmax的Visual范围内同伴数量num满足numN<δ,(0<δ<1),则表明Xmax周围营养物质丰富且鱼群数量适当,则向Xmax的方位前进1步:

(13)
否则执行步骤1.
4) 随机行为.人工鱼在Visual范围内执行式(14),选择下一个位置,并移向该方位:

(14)
5) 公告板.用来记录人工鱼在全局搜索过程中每次迭代的最优值.
2 自适应人工鱼群FCM的异常检测算法
自适应人工鱼群FCM的异常检测算法主要包括3个部分:1)提出自适应AFSA;2)将其应用于FCM中;3)提出基于自适应人工鱼群FCM的异常检测算法.
2.1 自适应人工鱼群算法
2.1.1 算法过程及时间代价分析
AFSA算法中,觅食行为是AFSA收敛的基础.其中,Visual选择适当与否直接影响到最终的结果.经实验发现,导致算法迭代次数增加的根本原因是由于Visual值固定不变.在最优解的搜索过程中,会有较少部分的人工鱼有别于公告板上记录的最佳状况.如果给定的Visual参数值偏大,则算法初期收敛很快,但当逼近最优解时会增加迭代次数,且试探次数TryNumber会增多,影响算法的执行效率;如果给定的Visual参数偏小,则会使收敛速度变慢,增加计算量,算法容易陷入局部极小值,不能得到全局最优解.
为了解决上述问题,本文对觅食行为的Visual选取进行改进,使其根据当前迭代状态进行自适应计算取值,从而提出自适应人工鱼群算法(adaptive artificial fish swarm algorithm, AAFSA).其基本思想是:Visual取值随迭代次数的增加而自适应减少.同时,为了避免后期Visual太小而影响最终结果,设定一个下限阈值,当Visual值小于该阈值时,就停止减少.这需要根据具体问题来设置该值.Visual值设定的计算方法为
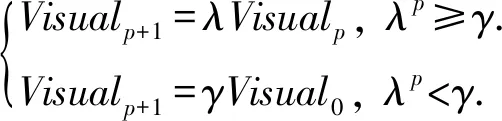
(15)
其中,λ∈(0,1)为衰减因子,p为迭代的计数器(最大值为P),γ∈(0,1)为Visual的下限阈值.AAFSA算法过程及分析:
Step1. 初始化N条人工鱼.其时间复杂度为O(N),初始化其他参数的时间复杂度为O(1).
Step2. 初始化公告板.需要赋值1次,比较N-1次,时间复杂度为O(N).
Step3. 聚群行为.计算δ需要N次,判断1次,移动1次,N条人工鱼聚群N次.因此时间复杂度为O(N2+2N).
Step4. 追尾行为.计算拥挤因子需要N次,寻优N次,N条人工鱼需要追尾N次.因此时间复杂度为O(2N2+2N).
Step5. 觅食行为.需要试探TryNumber次,最少1次,N条人工鱼需要觅食N次.故时间复杂度为O(N×TryNumber).
综上,由于AAFSA经过的最大迭代次数P,则算法时间复杂度为O(P×(3N2+N×TryNumber+6N))≈O(PN2).这种时间代价是可接受的.
2.1.2 算法收敛性证明
AAFSA是可收敛到全局最优解的.我们可以通过建立吸收态Markov过程模型来证明.

P(X(tn)=Xn|X(tn-1)=Xn-1,…,X(t1)=X1)=
P(X(tn)=Xn|X(tn-1)=Xn-1),
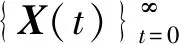
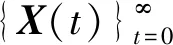
P(X(t+1)∉Y*|X(t)∈Y*)=0,
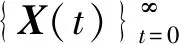
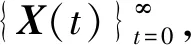
P(X(t)|X(t-1),X(t-2),…,X(0))=
P(X(t)|X(t-1)),
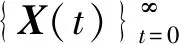
由AAFSA聚群、追尾和觅食行为可知,当X(t)∈Y*为最优解空间时X(t+1)∈Y*,因此:
P(X(t+1)∉Y*|X(t)∈Y*)=0,
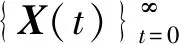
证毕.
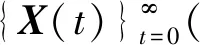
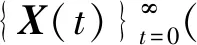
P(X(t)∈Y*|X(t-1)∉Y*)≥d(t-1)≥0
且
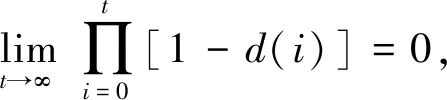
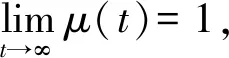
证明. 根据全概率公式,
μ(t)=[1-μ(t-1)]P(X(t)∈Y*|X(t-1)∉Y*)+
μ(t-1)P(X(t)∈Y*|X(t-1)∈Y*),
(∀t=1,2,…).


证毕.
定理1.AAFSA以概率1收敛到全局最优解.
证明. 假设问题的求解空间为Ω.设其有m个局部最优区域:Ω1,Ω2,…,Ωm.
在AAFSA迭代过程中,一定会有人工鱼搜寻到某一局部最优区域.设其为Xi,进入的局部最优区域为Ω1,则由引理2可知,Xi收敛到Ω1的最优值Y1.
AAFSA在进行聚群与追尾时,由δ进行控制着目标位置人工鱼的稠密程度.当密度超过δ时,人工鱼会向其他区域移动.因此,当Ω1满负荷后,其他人工鱼会搜索余下区域,从而得到第2个局部收敛区域,设为Ω2.同时该人工鱼也会收敛到Ω2最优值Y2.
同理,剩下的Ω3,Ω4,…,Ωm,其局部最优解分别为Y3,Y4,…,Ym.另外,在AAFSA中,每次迭代的Visual取值是可计算的,不会影响迭代趋向.公告板记录以上最优解,当算法满足结束条件时,输出公告板记录,即Y最优=max{Y1,Y2,…,Ym}
综上,AAFSA以概率1收敛到全局最优解.
证毕.
2.2 基于自适应人工鱼群的FCM算法
基于自适应人工鱼群的FCM算法,即AAFSA-FCM,可以很好地利用AAFSA的优势来解决FCM算法对初始值过于依赖,易于陷入局部极值的问题.其算法思想是:使用AAFSA,迭代计算问题最优解.然后将该解作为FCM的初始聚类中心,进行迭代聚类分析,将不同类型的样本划分到不同簇类中.算法流程如图2所示.

Fig. 2 Flow chart of AAFSA-FCM图2 AAFSA-FCM算法流程
基于自适应人工鱼群的FCM算法有2个关键:问题空间编码和适应度函数的确定.
1) 编码.本算法采用基于初始聚类中心的编码格式对样本数据进行编码,即由n个初始聚类中心来构成每条人工鱼的位置信息.设s为问题空间的维度,则人工鱼的位置是n×s维变量:
Pn=(c11,c12,…,c1s,…,ci1,…,ci2,…,cis,…,cns).
(16)
2) 适应度函数.在FCM算法中,目标函数J(由式(3)计算)的最小值即为最优的聚类结果.其值越小则聚类效果越明显.因此,设定本算法的适应度函数:
f=1(J+1).
(17)
由式(17)可以知道J的值越小,f的值越大,聚类效果越明显.
具体而言,AAFSA-FCM算法步骤:
Step1. 设定人工鱼数目N、移动步长Step、模糊指数m、试探次数TryNumber、δ、聚类划分数目c、搜寻范围Visual等各个参数值;
Step2. 根据人工鱼的位置,将当前结果与公告板上的记录进行对比分析,选取较优值并更新公告板上的信息;
Step3. 根据式(6)与式(3)计算样本聚类中心和目标函数的初始值,并进行适应度评价;
Step4. 执行AAFSA觅食、聚群、追尾行为;
Step5. 更新人工鱼的状态,并根据式(15)自适应调整Visual值;
Step6. 与结束条件进行对比,若满足结束条件,则将结果作为FCM聚类的初始值,转至Step7继续执行FCM聚类分析过程;若不满足,则转到Step2继续执行AAFSA过程.
Step7. 利用FCM算法,进行不断的迭代计算,直至满足约束条件,得到最终的结果.
算法1.AAFSA-FCM的伪代码.
输入:给定数据样本集A、初始人工鱼规模N、移动步长Step、搜寻范围(视野)Visual、试探次数TryNumber、算法的迭代次数P、拥挤因子δ、聚类数目c、模糊指数m、人工鱼状态X、目标函数(食物浓度)Y;
输出:A的c个最优的聚类划分C.
Begin:
AF_prey()
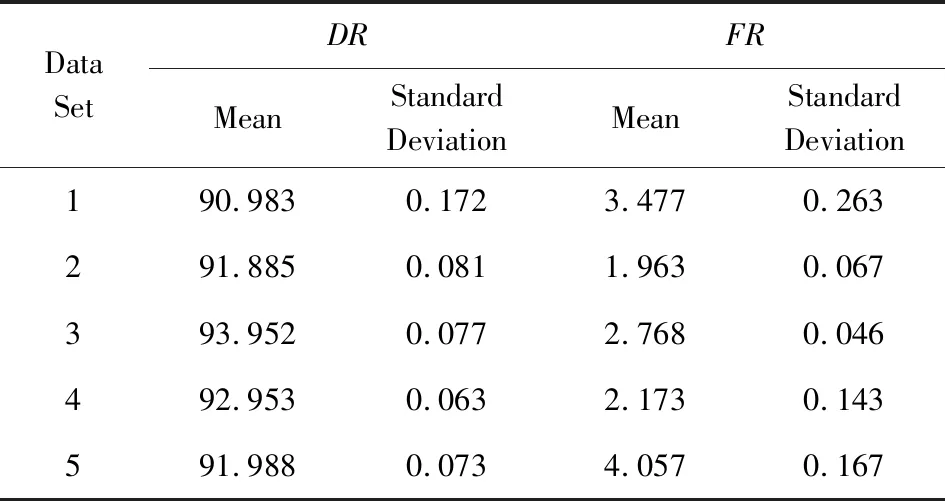
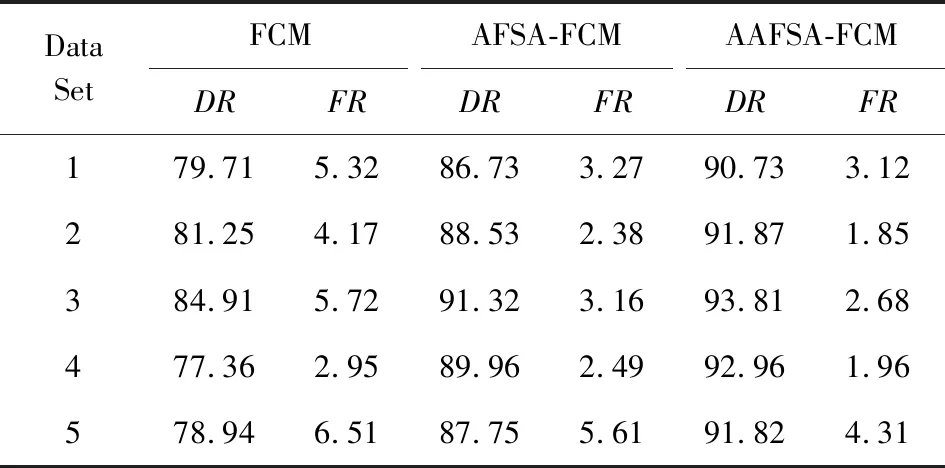
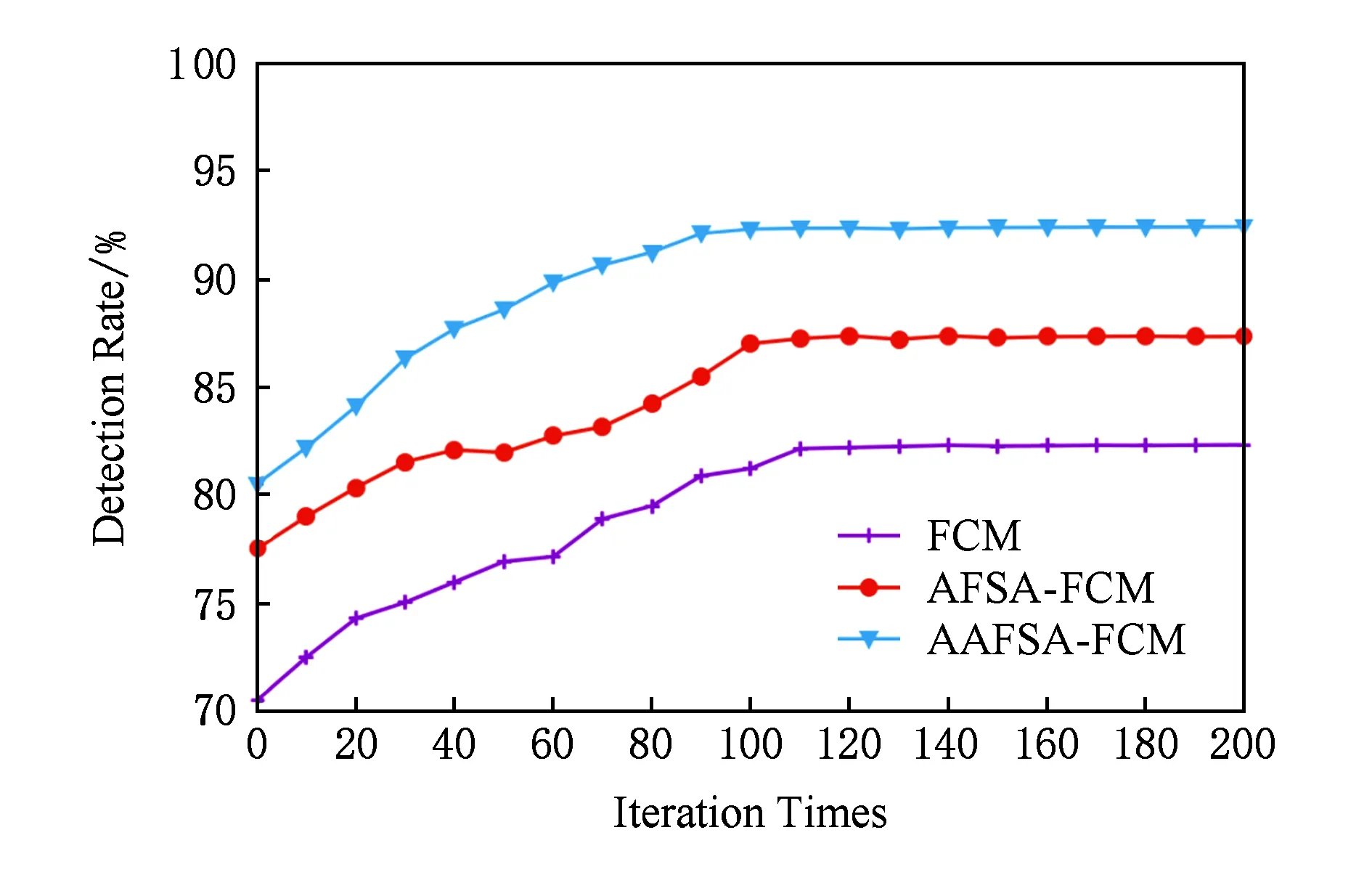
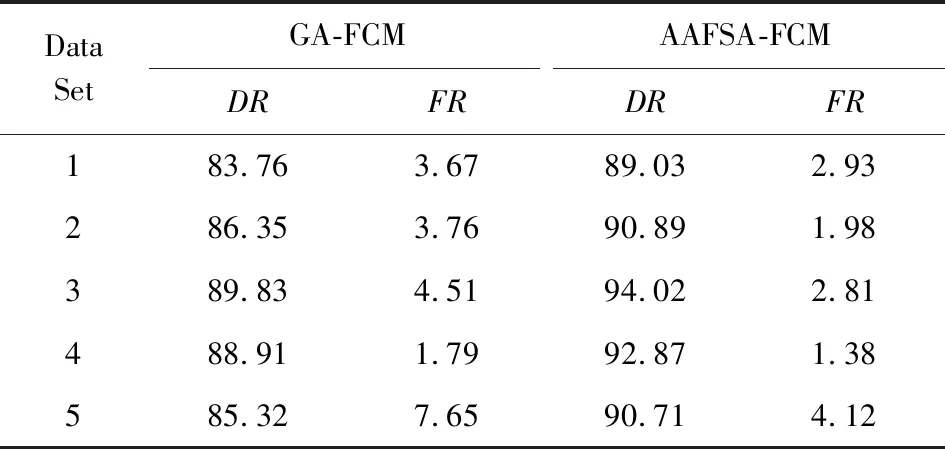
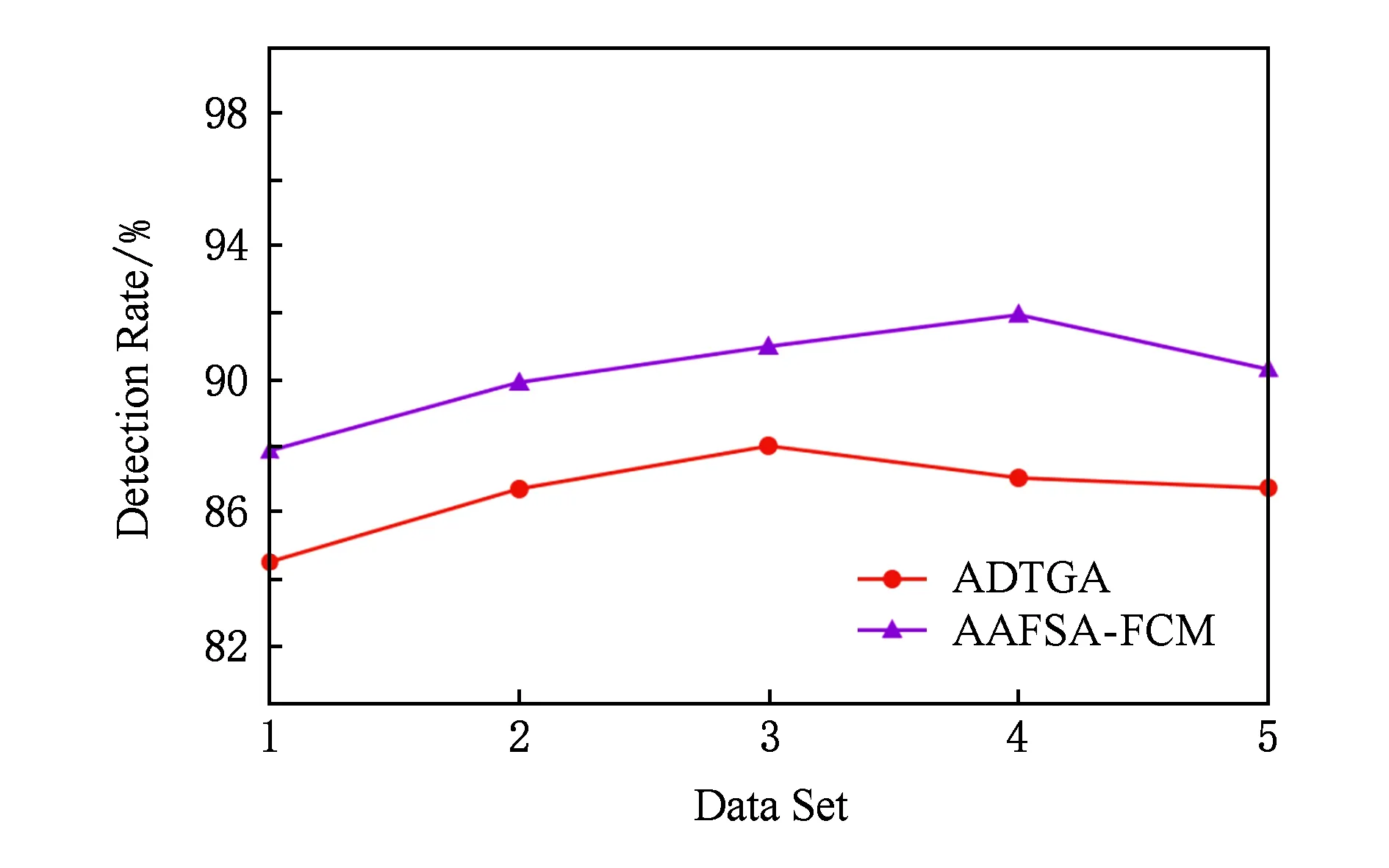
for (i=0;i Xj=Xi+Visual·R; if (Yi>Yj)*当前食物浓度大于随机位置浓度* endif endfor AF_swarm() for (j=0;j if (di,j num++;Xc+=Xj; endif if (numN<δ&&Yi>Yc) elseAF_prey(); endif endfor AF_follow() for (j=0;j if (di,j Ymax=Yj;Xmax=Xj; endif for (j=0;j if (dj,max endif endfor elseAF_prey(); endif endfor doAAFAS() while (p for (j=0;j AF_prey();AF_swarm();AF_follow(); bulletin();*与公告板进行比较* endfor p++; endwhile C=FCM(c); End 结合之前的算法分析可以看出,AAFSA-FCM总的时间复杂度为O(PN2)+O(nlcf).这种时间代价是可接受的. 引入AAFSA对FCM算法进行优化可以使其更好地作用于异常检测.因此,设计基于AAFSA-FCM的异常检测算法,其算法流程: Step1. 将训练数据放入矩阵Xn×l中; Step2. 根据编码规则,为每条人工鱼赋初值; Step3. 根据AAFSA进行计算,直至满足终止条件; Step4. 将Step3得到的最优结果作为FCM的初始值; Step5. 对测试数据集Xn×l标准进化处理: 其中,max(i)和min(i)分别表示该属性的最大值与最小值; Step6. 根据FCM算法,进行迭代计算.当满足算法的终止条件时,得出异常样本集合. 其中,在FCM算法对数据集进行检测时,设定每捕获到一定量的数据就将其整理成Xn×l矩阵.若有异常则发出警告. 从以上各个部分的时间代价分析中可以看出,AAFSA-FCM异常检测的时间复杂为O(PN2)+O(nlcf)+O(nl)≈O(PN2)+O(nlcf).这种时间代价是可接受的. 实验首先选用UCI seeds数据集和Iris数据集进行聚类分析.UCI seeds数据集样本,共8维属性,可分为3类,每类样本含有70条数据,共210条数据,每条数据含有7种属性;Iris数据集,共4维属性,也包括3类样本,每类样本包含50条数据,共150条数据. 进行对比实验前,首先要确定AAFSA涉及的主要参数取值.各参数及其对算法性能的影响简述: 1) 人工鱼规模N.AAFSA通过自适应调整视野,提高个体的利用率.增加鱼群数量,能够提高整体寻优性能,但运算量也会增加. 2) 最大迭代次数P.随着迭代次数的不断增加,鱼群不断聚集,视野不断缩小,寻优精度逐步提高,最终在某点聚集.此时再增加迭代次数,对寻优的影响不大. 3) 试探次数TryNumber.增加试探次数,能够提高觅食行为的概率.对于一般的优化问题,适当地增加试探次数,能够提高收敛速度以及寻优精度. 4) 步长Step.适当的步长增加,能够减少迭代次数,但步长过大,迭代次数会增加以及收敛速度减慢. 5) 视野Visual.在步长一定的情况下,适当地增加视野,迭代次数略有减少,而较小的视野可使算法收敛效果更好. 6) 拥挤度因子δ.拥挤度因子越小,摆脱局部极值的能力越强.而且,拥挤因子的不断增加,迭代次数会增加以及收敛速度减慢. 本文在确定这些参数时,按参考文献[25]方式进行多次实验,根据所选测试数据集的实际情况,选取其最优值:N=40,最大的迭代次数P=200,TryNumber=50,Step=0.5,Visual=3,δ=0.8,λ=0.5,γ=0.5.另外,FCM中的m=2,c=3. UCI seeds数据集聚类结果如图3和图4所示,Iris数据集聚类结果如图5和图6所示(降维聚类,每维属性为其他维度属性的线性组合,无明确单位).从图3~6中可以看出,FCM的划分效果比较模糊,类内比较松散,各样本点距离聚类中心的位置比较远,类间没有较为明显的划分界限,聚类的正确率比较低.这就说明,在FCM聚类过程中,原始算法没有选到最优的聚类中心.而AAFSA-FCM簇类划分的效果相对较好,类内比较紧凑,类间的划分界限相对明显,聚类正确率明显高于FCM.这就说明:AAFSA-FCM寻找的聚类中心相对较优,FCM聚类效果才会相对较好. Fig. 3 Results of FCM with UCI seeds data set图3 UCI seeds数据集的FCM效果 Fig. 4 Results of AAFSA-FCM with UCI seeds data set图4 UCI seeds数据集的AAFSA-FCM效果 Fig. 5 Results of FCM with Iris data set图5 Iris数据集的FCM效果 Fig. 6 Results of AAFSA-FCM with Iris data set图6 Iris数据集的AAFSA-FCM效果 本实验分3部分:1)基于AAFSA-FCM的异常检测稳定性实验;2)基于FCM,AFSA-FCM,AAFSA-FCM的异常检测对比实验;3)基于AAFSA-FCM、基于GA-FCM和基于决策树的异常检测对比实验. 实验采用本领域知名的KDD CUP 1999数据集,首先需要进行数据预处理,将离散型属性转换成连续型属性,例如其中的协议属性,实验设定的变换规则为:TCP→1,UDP→2,ICMP→3等.然后,从中随机抽取6组样本进行实验.设定其中1组为训练数据集,含有30 000条记录,其中异常记录363条.剩余5组作为测试数据集,每组均含有10 000条记录,其中120为异常记录. 评价异常检测性能优劣一般需要计算检测率(detection rate,DR)与误报率(false-positive rate,FR),其定义: 算法相关参数设定过程同3.1节实验,并参照文献[17]将各个参数设置为:N=50,P=200,TryNumber=50,Step=0.8,Visual=4,δ,λ,γ均取值为0.5,FCM中的m=2,c=5. 3.2.1 AAFSA-FCM异常检测稳定性实验 异常检测的稳定性十分重要,可通过多次实验进行均值和标准差计算进行衡量.本部分实验由2部分组成: 1) 为了验证算法对不同测试数据集的效果,也验证算法每捕获到一定量的数据进行一次集中处理的方式的可行性,我们从测试数据集中随机抽取6组数据,每组包含1 000条数据组成Xn×l矩阵进行实验,结果汇总如图7所示.从图7可以看出,每次随着测试数据选择的不同,算法表现出了不同的检测性能,但波动在可接受范围内.出现波动的主要原因是算法对不同异常的认知能力是不同的. Fig. 7 DR of AAFSA-FCM with different test matrixs图7 AAFSA-FCM对不同测试矩阵的检测率 2) 为了测试不同测试数据集内部本算法的检测稳定性,我们对每组数据集反复进行5次实验,结果汇总如表1所示.从表1可以看出,AAFSA-FCM在参数相同的情况下,不同组测试集的DR与FR的均值不同,但结果较为满意,而标准差均在合理变化范围内.这是由于本实验所选的训练集和测试集是随机抽取的样本,数量有限,而且包含的异常样本的特征也不尽相同.总体来看,基于AAFSA优化的FCM异常检测拥有较为理想的检测性能,特别是在稳定性方面表现尤为突出. Table 1 Detection Results of AAFSA-FCM with Different Test Sets表1 不同测试集下AAFSA-FCM的检测结果 % 3.2.2 基于FCM,AFSA-FCM,AAFSA-FCM的异常检测实验结果 为了验证加入AAFSA后的FCM异常检测的性能,本实验将上述5组测试集分别使用基本的FCM,AFSA-FCM,AAFSA-FCM异常检测对其进行测试,所用参数相同,结果汇总如表2、图8~10所示. Table 2 Detection Results of FCM, AFSA-FCM and AAFSA-FCM表2 FCM,AFSA-FCM,AAFSA-FCM的检测结果 % Fig. 8 DR comparison with three algorithms图8 3种算法检测率对比 Fig. 9 FR comparison with three algorithms图9 3种算法误报率对比 表2和图8~9为最终3种算法的检测性能对比.从表2和图8~9中可以看出,不同测试集下,AAFSA-FCM异常检测的DR均高于FCM和AFSA-FCM异常检测的结果,而且,其FR均低于另外2个算法的FR.总体来看,AAFSA-FCM异常检测方法取得较好的结果. 图10所示为在不同迭代周期里3种算法在其中1组测试集下的检测率对比.从图10可以看出,AAFSA-FCM异常检测在迭代次数为85时效果已经可以达到最优值.而另外2种算法则需要100~110次迭代后才可以达到较为理想的结果,但结果也比AAFSA-FCM异常检测要差一些. Fig. 10 DR comparison with three algorithms in different iteration cycles图10 3种算法在不同迭代周期里的检测率对比 这是由于AAFSA对AFSA进行了优化,自适应调整Visual取值,提高AFSA局部和全局寻优能力,减少了算法的迭代次数,使其不易陷入局部极值,从而获得全局最优解.而且这一改进显著提高了算法的运行效率.然后,将AAFSA与FCM相结合,可以很好地解决FCM算法对初始值过于依赖,容易陷入局部最优的问题.最后,充分利用AAFSA与FCM二者的优点,基于此设计的异常检测算法能够获得较好的检测结果. 3.2.3 基于AAFSA-FCM和GA-FCM的异常检测对比实验 为了更进一步对比AAFSA与其他优化策略的效果,本部分实验选取AAFSA-FCM异常检测与文献[8]提出的GA-FCM异常检测算法进行对比实验.本算法实验条件和参数设置同上,GA-FCM的参数设定参考文献[8],其中种群规模为100,交叉概率为0.8,变异概率为0.1,进化代数为200.对比结果如表3所示.从表3可以发现,AAFSA-FCM异常检测在每组测试集中的实验均取得较好的结果,FR均高于GA-FCM异常检测,FR均低于GA-FCM异常检测. AFSA与GA的基本思路都是随机初始化,根据目标函数进行寻优搜索.GA容易过早收敛而陷入局部极小值,同时对初始种群依赖程度高,初始种群选择的优劣直接影响算法的性能以及最终的寻优结果.而AFSA的鲁棒性更强,易于实现且全局收敛性更好,而且加入了自适应机制的AAFSA具有更好的收敛性.这些特点都很好地体现在实验结果中. Table 3 Detection Results of AAFSA-FCM and GA-FCM表3 AAFSA-FCM和GA-FCM的检测结果 % 3.2.4 基于AAFSA-FCM和ADTGA的异常检测对比实验 为了比较AAFSA-FCM算法与其他类型异常检测方法的的性能优劣,本部分将该算法与李建中在文献[26]提出的基于精确决策树生成算法(accurate decision tree generation algorithm, ADTGA) 的异常检测方法进行对比.决策树和聚类分析是不同作用机制的方法,都在异常检测等相关领域中得到了很好的应用.AAFSA-FCM算法实验条件和参数设置同上,对比文献中ADTGA相关实验结果,绘图如图11所示: Fig. 11 Detection results of AAFSA-FCM and ADTGA图11 AAFSA-FCM与ADTGA的检测结果 从图11中可以看出,本文提出的算法性能更优.这主要是由于基于ADTGA的异常检测很难准确地检测到训练集中缺失的异常,从而降低整体性能.再通过与图8,9以及表3进行综合分析,本算法具有更好的收敛速度以及更高的检测率,具有更好的稳定性. 以上各个实验从不同角度测试AAFSA,AAFSA-FCM以及基于AAFSA-FCM的异常检测的不同性能指标,均得到不错的测试结果.说明改进AFSA并作用于FCM异常检测是可行和有效的. 本文针对AFSA在迫近最优解时,易于陷入局部最优的问题,引入自适应机制,随着算法迭代次数的增加自适应改变Visual的取值,从而提高AAFSA的局部和全局搜索能力.然后,利用其智能寻优和较好鲁棒性的特点,将其应用于FCM异常检测中,解决FCM对初始值过于依赖,易陷入局部最优而得不到最优解的弊端.实验表明:本文提出的AAFSA-FCM异常检测算法能够获得较好的检测性能. AAFSA-FCM异常检测经调整可以应用于多个应用领域,如网络安全中的入侵检测技术.基于FCM的入侵检测系统(intrusion detection system, IDS)是入侵检测重要的技术分支之一.基于AAFSA-FCM的IDS可对网络攻击样本集聚类划分,提高系统检测各种攻击的性能.实际运行中,与传统FCM算法比较,在保障系统检测性能有效提高的同时,算法的收敛速度和运行效率也相对较高,可较好地满足IDS的实时性要求.如何进一步兼顾IDS检测的精确度和实时性是未来研究的重点.
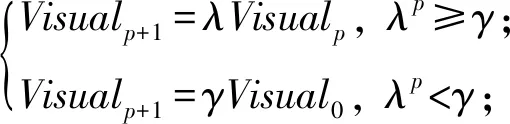
2.3 基于AAFSA-FCM的异常检测算法
3 实验结果与分析
3.1 FCM与AAFSA-FCM对比实验
3.2 AAFSA-FCM异常检测实验



4 总 结
