随机交通网络最小条件风险路径问题

潘义勇，陈 璐，丁 袁

(南京林业大学 汽车与交通工程学院， 江苏 南京 210037)

0 引 言

最优路径问题是图论的热点研究问题之一，也是交通网络均衡问题的核心子问题和车辆导航系统的核心问题[1]，由于交通网络的随机特性，传统的最优路径问题的建模及其求解算法难以满足实际交通情形的需要，因此需对随机交通网络环境下最优路径问题展开研究。

由于交通网络路径行程时间是一个随机变量，和传统的最短路径问题不同，不能简单的比较随机变量的大小，因此研究人员基于风险理论定义不同的路径目标函数，建立不同的随机交通网络环境下的最优路径模型。最小期望路径问题是最先提出来的模型[2]，最小期望路径是以期望值为路径的目标函数，没有考虑由于交通网络随机特性带来的路径风险性。在交通实际情形中驾驶员不仅关注行程时间的期望值最少而且关注行程时间的风险性最小[3-4]，因此研究人员开始在路径目标函数中加入风险指标，主要有：最小期望-均方差路径问题[5-7]，最大可靠度路径问题[8-9]，α-可靠路径问题等[10]，最小期望-均方差路径问题的路径目标函数是期望值和均方差的线性组合，其优点是综合考虑了期望值和均方差，其缺点是线性组合的比例系数需要人为设定，具有随意性，不能统一解释考虑风险的路径选择行为。最大可靠度路径问题的路径目标函数是可靠性理论中的重要指标：可靠度，其优点是直接反映了路径的风险性，其缺点是需要事先设定一个期望到达终点的时间，但是现实中驾驶员一般不知道到达终点的时间。α-可靠路径问题中的路径目标函数是风险理论中的重要风险指标：风险值[11]，风险值不需要事先设定一个期望到达终点的时间，只需给定一个风险置信水平，在严格确保风险置信水平的前提下寻找期望值最小的路径，风险值虽然反映了路径行程时间的风险性，但是过于严格，不能反映实际路径选择中超出期望时间的容忍度，因此笔者引入风险理论中的另外一个风险指标：条件风险值，该指标优点是准确反映交通网络中群体考虑风险的路径选择行为和对超出风险值的不可靠性弹性容忍的路径选择行为[12]。风险理论在金融学领域已经发展的相当完善，研究投资者在金融领域的投资行为，这和随机交通网络路径选择行为具有高度的相似性，交通网络最优路径研究可以借助现有的风险理论研究方法与结论进一步拓展改善，推动整个最优路径导航系统理论的发展。

定义条件风险值为路径目标函数，建立随机交通网络束最小条件风险路径问题数学模型并对其求解算法展开讨论。首先，为了反映交通网络中风险规避的路径选择行为，引入风险理论中的条件风险值指标，建立随机交通网络环境下最小条件风险路径问题数学模型，证明了路径目标函数条件风险值的次可加性，把最小条件风险路径问题转化为基于路段的最小条件风险路径问题；其次，构造基于动态规划的标号算法求解该问题；第三，编写计算机算法程序，并针对实际交通网络：Sioux Falls Network展开数值试验并对计算结果进行了分析。最后，总结了研究成果的应用性以及进一步研究的方向。

1 问题描述与建模

(1)

其中：

(2)

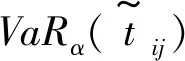
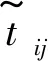
x={xij∈{0,1}|(i,j)∈A}

(3)

其中：xij=1表示边(i,j)在先验路径x上，xij=0表示边(i,j)不在先验路径x上。此时先验路径x上的随机行程时间为

(4)

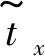
(5)

其中：

(6)

针对以上的路径目标函数，随机交通网络环境下最小条件风险路径问题建模为以下0～1整数规划问题：

(7)

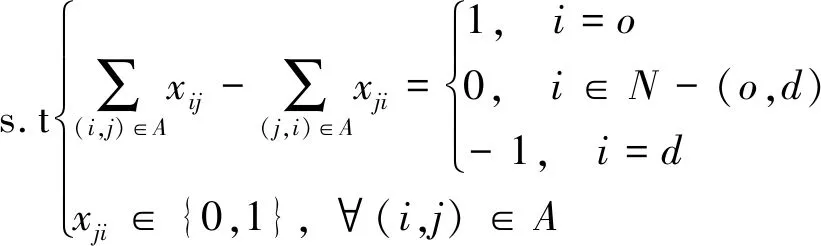
(8)

由于条件风险值的不可加性，公式(7)的路径目标函数是不可加的，因此不能采用常用的基于动态规划的标号算法求解该问题，下面我们对上述基于路径的最小条件风险路径问题进行松弛，证明基于路径的条件风险值满足次可加性。

定理1：

(9)

证明：

(10)

(11)

(12)

(13)

其中：

Z3=E[t～ij|∑(i,j)∈At～ijxijVaRα(∑(i,j)∈At～ijxij),t～ij>VaRα(t～ij)]1=E[t～ij|∑(i,j)∈At～ijxij>VaRα(∑(i,j)∈At～ijxij),t～ij>VaRα(t～ij)]

定理1表明：一方面，随机交通网络环境下基于路径的最小条件风险路径问题的目标函数不具有可加性，因此基于路径的最小条件风险路径不满足Bellman准则[13]，不能通过基于动态规划的算法来解决该问题；另一方面，路段的条件风险值之和是路径的最小条件风险值的上界。因此我们可以把路段的条件风险值之和作为路径的目标函数，构造基于路段的最小条件风险路径问题模型。

定义2：(基于路段的最小条件风险路径)给定风险置信水平α，x*是基于路段的最小条件风险路径当且仅当x*=argmin{∑(i,j)∈ACVaRα(t～ij)xij,∀x}。

针对以上的路径目标函数，基于路段的最小条件风险路径问题建模为下列混合非线性整数约束优化问题：

minf′(x)=∑(i,j)∈ACVaRα(t～ij)xij=

∑(i,j)∈AEt～ij|t～ij>VaRα(t～ij)xij

(14)

s.t{∑(i,j)∈Axij-∑(j,i)∈Axji={1, i=o

0, i∈N-(o,d)

-1, i=d

xji∈{0,1}, ∀(i,j)∈A

(15)

由于基于路段的最小条件风险路径问题的目标函数的可加性，也就表明基于路段的最小条件风险路径的任意子路径都是基于路段的最小条件风险子路径，满足动态规划的Bellman准则，因此我们可以通过基于动态规划的算法来解决该问题。

2 求解算法

本节构造基于动态规划的标号算法求解基于路段的随机交通网络最小条件风险路径问题，标号算法是一种求解动态规划问题的最常用算法，具体的程序算法见表1。

表1 基于动态规划的标号算法

步骤1：初始化。给起点o∈N标上永久标号P标号：P(o)=0，其余各点标上临时T标号：T0(j)=+∞，表示从o∈N到o∈N最短路权为0，从o∈N到各点的最短路权的上界为+∞。

步骤2：修正临时标号。设i是前一轮标号(第K-1轮标号)刚得到P标号的点，则对所有没有得到P标号的点进行新的一轮标号(第K轮)。考虑所有与i相邻并没有标上P标号的点j，修改j的T标号为：

TK(j)=min[T(j),P(i)+CVaRα(t～ij)]

(16)

式中：T(j)为第K轮标号前Vj点已取得的T标号。

步骤3：修正永久标号。在所有的T标号中，寻找一个最小的T标号TK(j0)方式为

TK(j0)=min[TK(j)]

(17)

给点Tj0标上P标号，即：

P(j0)=TK(j0)

(18)

步骤4：判定算法终止。若N中已没有T标号点，则算法结束，否则转入步骤2。

3 数值试验

通过MATLAB计算机语言编写基于动态规划的标号算法求解上述随机交通网络环境下最小条件风险路径问题，并且在Windows-10 (64) 工作站(two 2.00 GHz Xeon CPUs and 4G RAM )条件下运行的。Sioux Falls Network是国际常用的交通测试网络，其拓扑结构如图1。

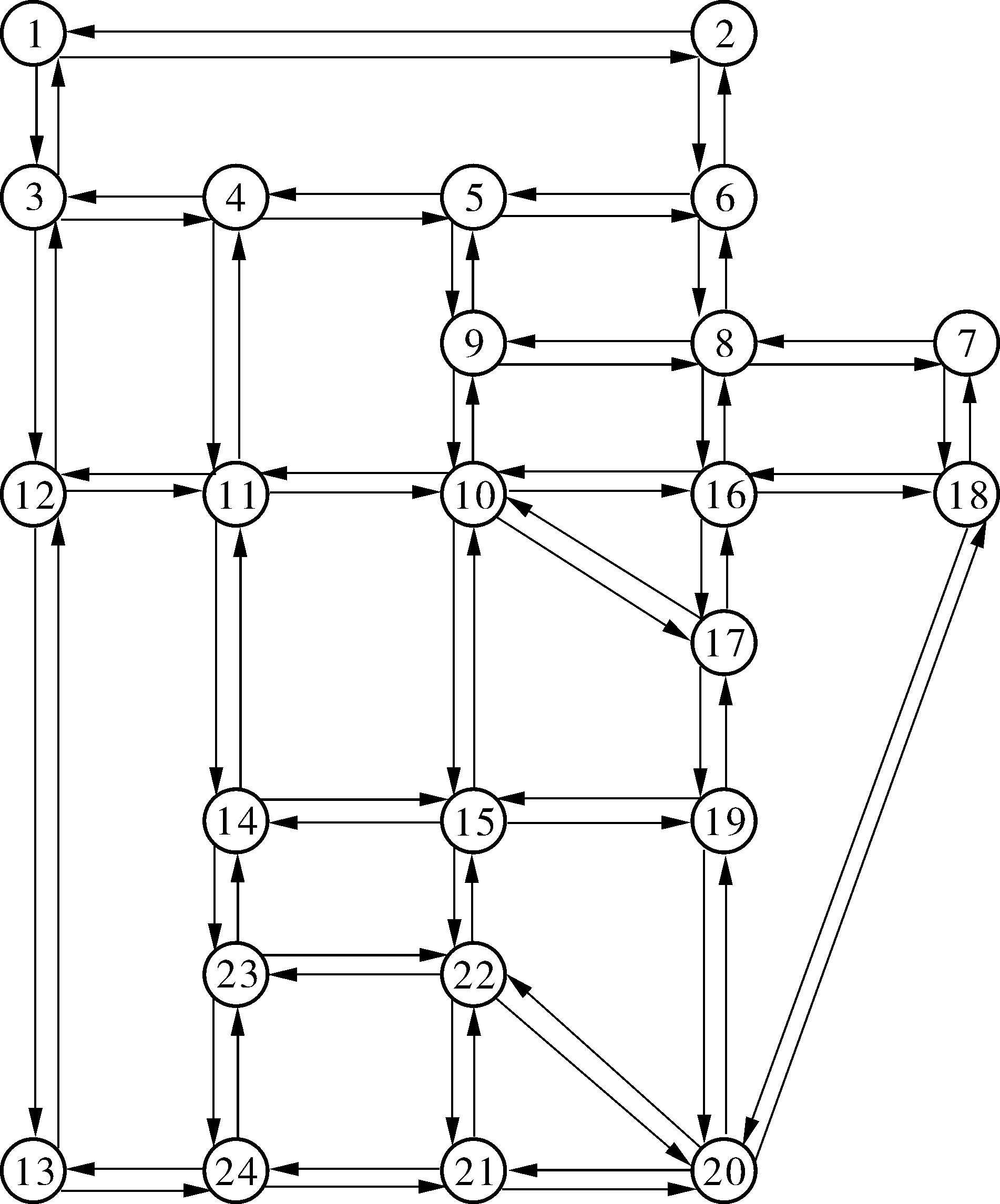
图1 苏福尔斯网络

为了仿真交通网络行程时间的随机特性，设定交通网络中每个路段的行程时间服从正态分布t～ij～N(μij,σ2ij)，不同的概率分布的设定不影响数值试验对本文的模型和算法的正确性和可行性的验证，本文的随机交通网络最小条件风险路径模型对网络中每个路段行程时间的概率分布是没有限制的，具有普适性。网络中每条边的期望值μij从区间[0,20]等概论随机取得，每条边的方差σ2ij从区间[0,10]等概率随机取得，根据条件风险值的定义，可以求得每个路段(i,j)的条件风险值为

CVaRα(t～ij)=E[t～ij|t～ij>VaRα(t～ij)]=μij+

k(α)σij

(19)

其中：k(α)={2π[exp(erf-1(2α-1)]22(1-α)}-1，erf(z)=2π∫z0e-t2dt。求在此随机网络环境下任意起点到任意终点的基于路段的最小条件风险路径。

表2给出了在风险置信水平α=0.5条件下，不同起迄点之间的最小条件风险路径和最小条件风险值。表3给出了不同风险置信水平条件下，起迄点13→8之间的基于路段的最小条件风险路径和最小条件风险值。表4给出了不同风险置信水平条件下，起迄点2→23之间的最小条件风险路径和最小条件风险值。从计算结果可以得出以下结论：

1)表2显示在风险置信水平α=0.5条件下，不同起迄点之间的期望值、条件风险值和基于路段的最小条件风险路径是不同的，表3显示起迄点13→8在不同风险置信水平条件下，其求解的基于路段的最小条件风险路径及其期望值、条件风险值是不同的，表4显示起迄点2→23在不同置信水平条件下，其求解的基于路段的最小条件风险路径及其期望值、条件风险值是不同的。由此可以看出，在相同的风险置信水平条件下，起迄点之间的基于路段的最小条件风险路径是不同的，在不同风险置信水平条件下，相同的起迄点之间的基于路段的最小条件风险路径是不同的，风险置信水平条件对路径的选择具有重大的影响，这符合实际交通网络考虑风险性的路径选择行为的情形。

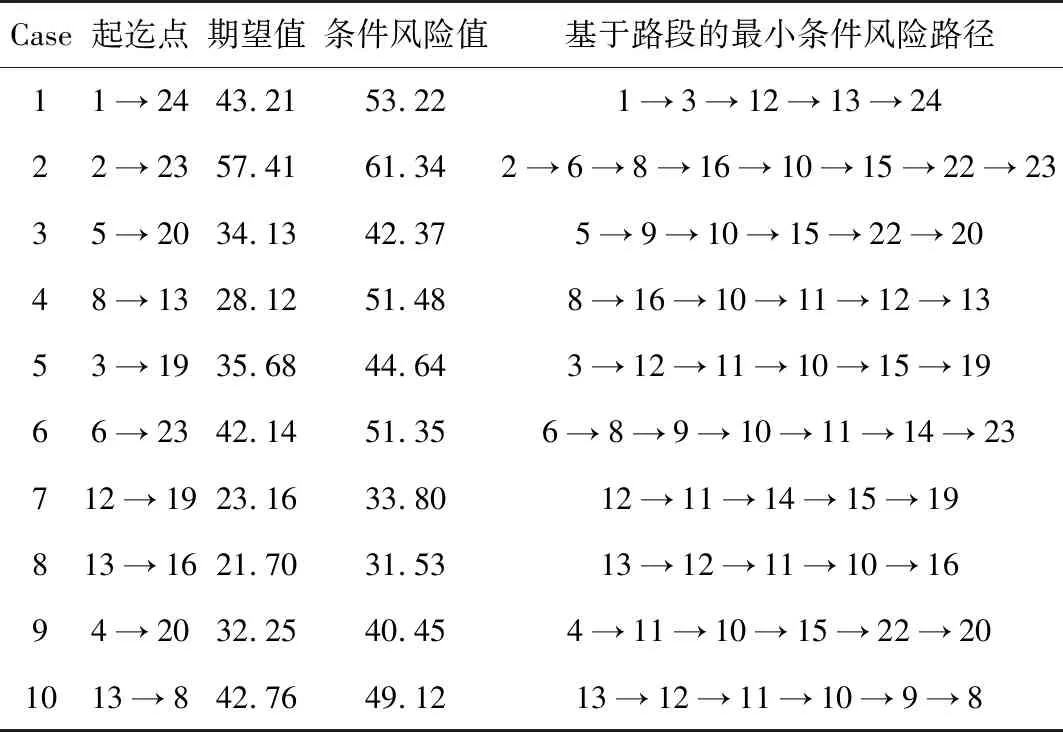
表2 不同起迄点之间的最小条件风险路径和最优值(α=0.5)

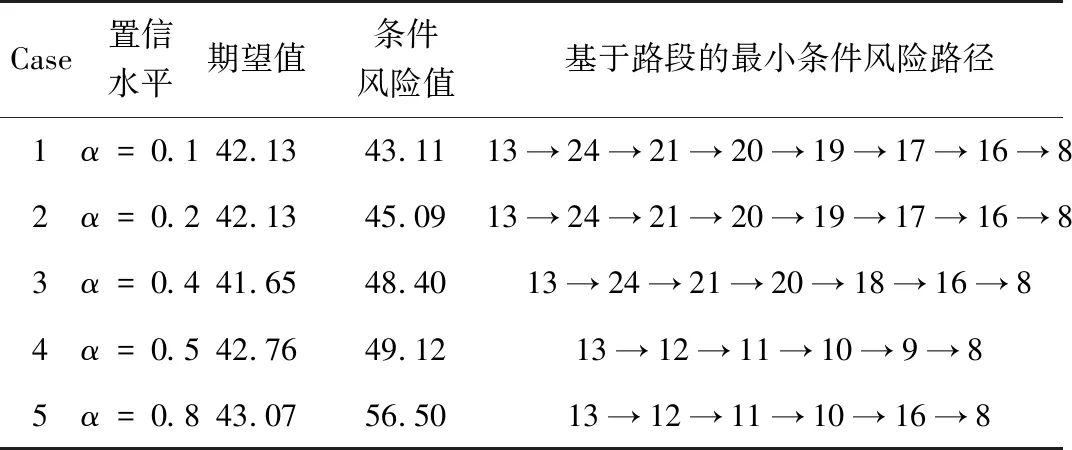
表3 不同置信水平条件下最小条件风险路径和最优值(13→8)

2)表2～表4显示了不同情形下获得基于路段的最小条件风险路径的条件风险值，并相应的计算了给路径的期望值，通过比较可以看出，获得的最优路径的条件风险值都比该路径的期望值要大，这符合风险理论中关于条件风险值的定义，也反映了交通网络中群体考虑风险的路径选择行为和对超出风险值的不可靠性弹性容忍的路径选择行为。

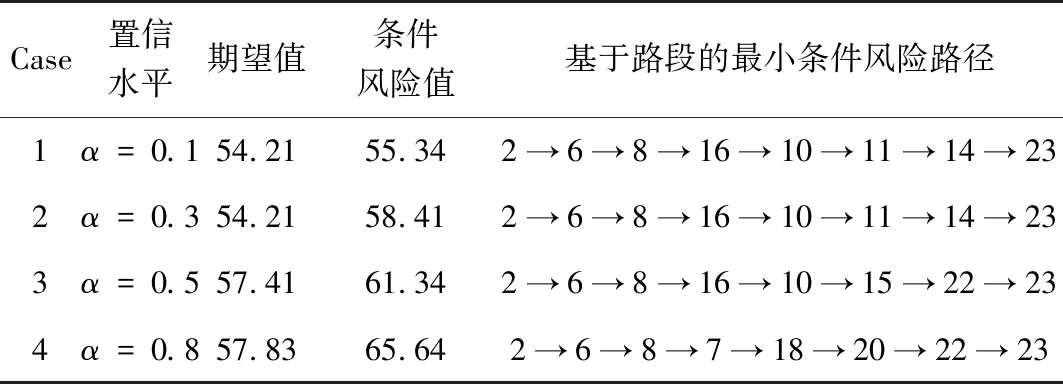
表4 不同置信水平条件下最小条件风险路径和最优值(2→23)

3)表3～表4显示在相同的起迄点之间，风险置信水平对最优路径的选择是有影响的，在起迄点13→8之间，当α=0.2,0.4,0.5,0.8时，其获得最优路径都是不同的，并且随着风险置信水平的增大，其相应的最优路径的条件风险值也是增加的，同样在起迄点2→23之间，当α=0.3,0.5,0.8时，其获得最优路径也是不同的，其相应的最优路径的条件风险值也是增加的。一方面，在实际交通网络中由于驾驶员不同的风险规避的要求，驾驶员选择的路径也是不同的；另一方面，随着风险置信水平的提高，驾驶员对交通网络中对路径行程时间超出风险值的不可靠性弹性容忍的期望值提高，这符合实际交通网络的路径选择行为。

4)笔者提出的标号算法能够求解随机网络环境下基于路段的最小条件风险路径问题的精确解，获得最优路径和其相应的最小条件风险值，能直接反馈给驾驶员，求解算法已经研究的很成熟，在优化软件中采用较多，这有利于我们进一步利用现有软件实现考虑风险性的最优路径的导航应用研究。

4 结 语

针对交通网络中群体考虑风险的路径选择行为和对超出风险值的不可靠性弹性容忍的路径选择行为，建立了随机交通网络环境下最小条件风险路径问题数学模型，证明了路径目标函数条件风险值的次可加性，把最小条件风险路径问题转化为基于路段的最小条件风险路径问题，构造基于动态规划的标号算法求解该问题，通过数值试验验证了该模型和算法的正确性和可行性。提出的随机交通网络环境下最小风险路径模型能更准确的反映交通网络中风险规避的路径选择行为，丰富了车辆导航系统的路径选择情形。提出的基于动态规划的标号算法是求解随机交通网络最小条件风险路径问题的有效算法，可以很好地应用在车辆导航系统。本研究假设随机网络中边的随机变量之间是相互独立的，没有考虑随机变量的相关性，考虑相关性的随机网络环境下约束最优路径问题需要进一步研究。