基于支持向量机法的混凝土强度对拼宽T梁桥时变可靠度影响分析
2019-05-14邬晓光何启龙肖凯龙
邬晓光, 何启龙, 2, 郑 鹏, 肖凯龙
(1.长安大学 桥梁与隧道陕西省重点实验室, 陕西 西安 710064; 2. 中铁大桥(南京)桥隧诊治有限公司,江苏 南京 210061)
0 引 言
在可靠度方面,拼宽桥较在役混凝土梁桥,相关的研究文献不多。目前,在拼宽桥结构可靠度方面,主要集中在影响因素的分析,如,刘国[1]、刘均利[2]等研究了钢筋锈蚀和混凝土碳化两种因素;董华平[3]、方志[4]等分析了沉降和收缩徐变等因素对主梁和下部结构的影响,董华平[3]建议增加收缩徐变的分析。以上针对拼宽桥的可靠度研究,多是依托横向分布系数法计算功能函数表达式来进行结构或体系可靠指标计算,偏不保守。当采用空间梁格法替换横向分布系数法的功能函数,较单梁推导时采用JC或MC法进行可靠指标的求解,过程则更为复杂。时变因素是影响桥梁结构可靠度的重要因素之一[5-6],包括材料的时变效应[5-8],如混凝土强度、钢筋锈蚀、混凝土碳化、收缩徐变[3]等。
预应力混凝土梁桥在设计时可忽略普通钢筋的贡献[5],仅作为构造钢筋。因此,笔者基于支持向量法(SVM法),研究相应的隐式函数拟合精度问题,并进行包含混凝土强度和收缩徐变等时变因素对拼宽桥可靠度的影响分析。
1 工程概况
依托某高速公路桥扩容工程,选择3 m×40 m连续拼宽T梁桥进行模型分析,拼宽桥横截面示意如图1,拼宽桥参数如表1。

表1 拼宽桥主要设计参数
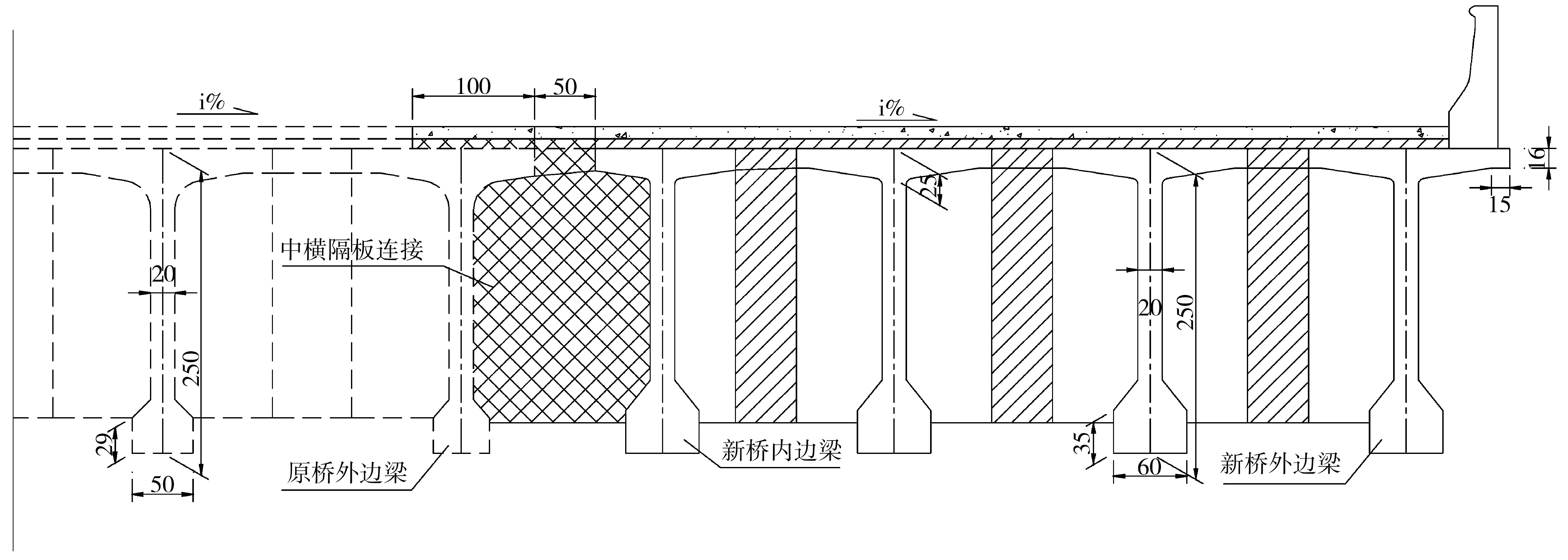
图1 连续T梁上部结构加宽断面示意(以跨中为例,单位:cm)Fig. 1 Diagram of widening section of the upper structure of continuous T-beam (an example of mid-span)
2 混凝土强度的时变效应规律
已有研究[8]表明:混凝土强度在浇筑3 d后逐渐增大,增长速率则逐渐下降;25~30 a后,强度开始下降,其下降速率略大于后期强度增加速率;一般的,10 a后强度约为28 d的1.5~1.9倍。
参考已有关于可靠度的研究[3-4],笔者同样认为混凝土后期强度仍不拒绝正态分布,并且强度的平均值和标准差仍为时间函数[9]。砼强度平均值函数:
μfcu(t)=μfcu0×1.452 9e-0.024 6(lnt-1.715 4)2
(1)
砼强度标准差函数:
σfcu(t)=σfcu0[0.030 5t+1.236 9]
(2)
式中:μfcu0为砼28 d立方体抗压强度平均值;μfcu(t)为t年后砼立方体抗压强度平均值;σfcu0为砼28 d立方体抗压强度标准差;σfcu(t)为t年后砼立方体抗压强度标准差。
混凝土强度服从的正态分布函数的参数与强度等级有关[11]。因此,参考文献[3],采用C50混凝土轴心抗压强度的统计参数,其值为N(39.6,4.3562)。为计算不同混凝土时变强度下的拼宽桥可靠度,新旧梁在不同运营时间(旧梁运营时间+新梁运营时间)下的混凝土轴心抗压强度统计参数如表2。

表2 不同运营时间的混凝土轴心抗压强度统计参数
3 正截面抗弯功能函数
一般的,预应力混凝土的功能函数参考钢筋混凝土桥[12],多忽略钢束二次力(Sp2)的影响,其荷载效应函数由恒荷载效应(SG)和活荷载效应(SQ)构成。
实际上,钢束二次力产生的不利效应对预应力桥影响较大,是桥梁荷载组合验算必须要考虑的因素之一,且文献[3]提出的收缩徐变引起的效应Ssc在可靠度研究中也应予以考虑。因此,令荷载效应S=SG+SQ+Sp2+Ssc进行可靠度研究。依托工程的左边跨跨中截面极限状态抗弯承载力功能函数[13]如式(3) ~ 式(6)。
1)受压区在T梁翼缘内,第一类T形截面:
(3)
(4)
2)受压区在T梁腹板内,第二类T形截面:
(5)
(6)
4 支持向量机法的应用原理
支持向量机法(SVM法),最早由V. N. VAPNIK[14]提出,是基于VC维理论和结构风险最小原理的一种学习方法,其体系结构如图2。该方法最初提出并用于处理样本点线性可分的最优分类面问题。若分析更多因素时,样本点则呈分布零散且非线性不可分,不直接适用回归模型;引入“非线性映射[15]”概念,将样本数据从低维度变换到高维空间,并在高维进行样本数据的线性超平面回归分析。

图2 支持向量机法的体系结构
SVM法在小样本分析中,可以取得较为理想的效果,且较传统的神经网络法、响应面法等更为简单易使用[16]。该方法目前多应用在手写识别、语音处理、文字、股市分析、人脸和文本识别等领域,在桥梁工程中应用较少,主要应用于斜拉[17]及连续刚构[18]等桥型。笔者则研究支持向量机法在拼宽梁桥中的可靠度分析问题,其流程如图3。

图3 SVM法拟合隐式函数的流程
5 基于支持向量机法的荷载效应隐式 函数拟合
在工程实际中,较为复杂结构采用空间有限元法计算时,相应的功能函数表达式无法具现,也无法直接采用JC法或MC法进行可靠指标的求解[3,13]。鉴于此,参考响应面法和神经网络法的隐式函数拟合流程[17],在小样本数据[16-18]条件下,采用SVM法构建荷载效应的隐式函数并用于拼宽桥的时变可靠度研究。
5.1 随机变量的统计参数
忽略非预应力钢筋对结构的抗弯承载力贡献后[13,18],其他随机变量的统计特征如表3,参数含义见文献[13]。预应力钢筋混凝土梁桥的结构承载能力计算需要考虑预应力的次内力(Sp2)影响。张拉控制应力假设服从正态分布[5],其均值为1 395 MPa,变异系数为0.05。1 860钢绞线弹性模量参考普通钢筋,假设同样服从正态分布[13],其均值为1.95×105MPa,变异系数为0.1。随机变量采用超拉丁LHS抽样法[20-21]进行小样本数据组抽样,并依托空间梁格法计算相应的响应值来构建SVM法所需的样本数据。

表3 各随机变量统计特征
5.2 荷载效应隐式函数拟合效果分析
采用支持向量机法对各新旧梁片在荷载效应组合(SG+SQ+Sp2+Ssc)下的隐式函数进行小样本数据拟合,如图4,其回归效果[18](R2)均接近于1,效果理想。
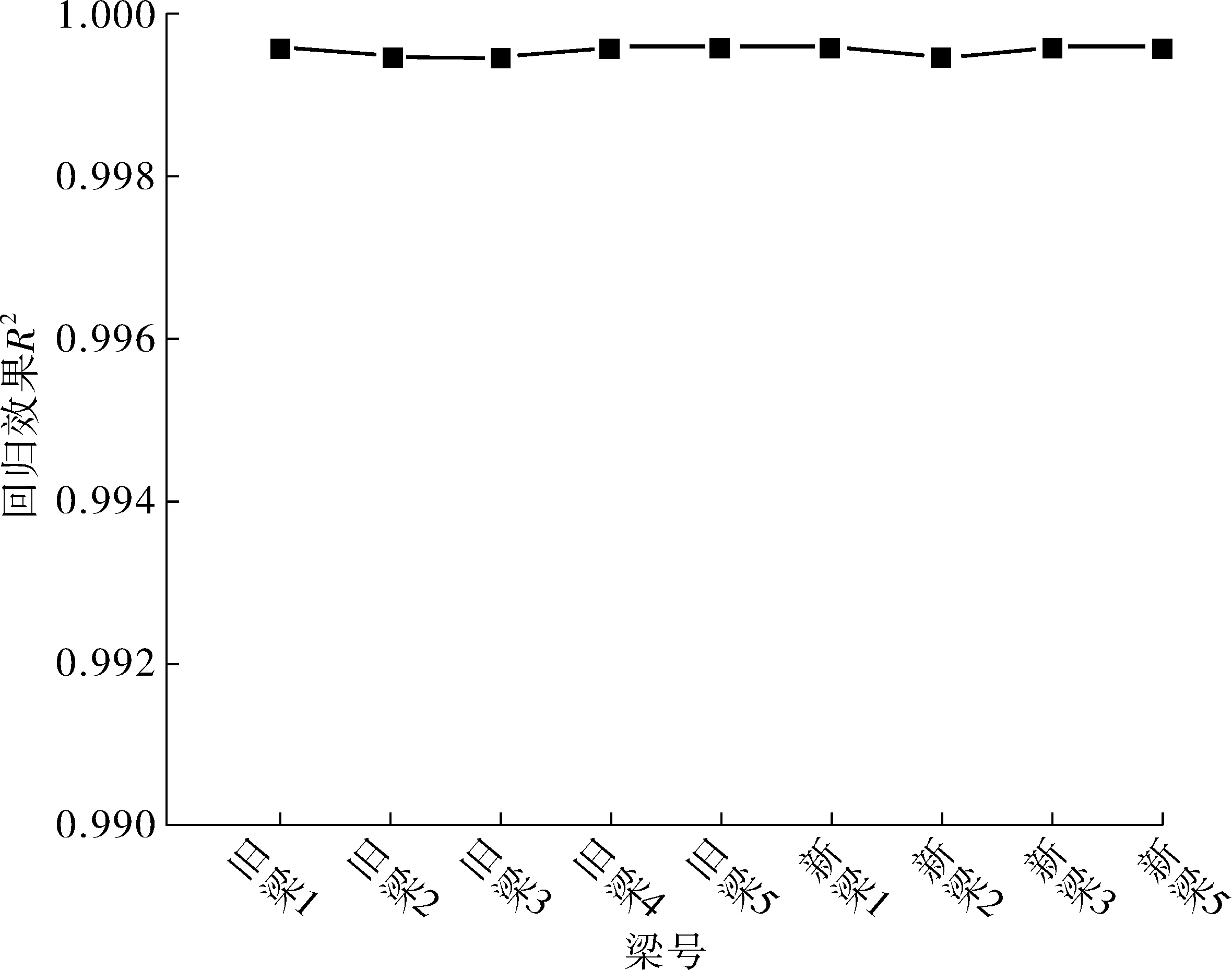
图4 荷载效应的隐式函数回归效果
以旧梁1为例,采用PSO算法进行参数寻优的效果如图5,小样本数据下的隐式函数回归效果理想。
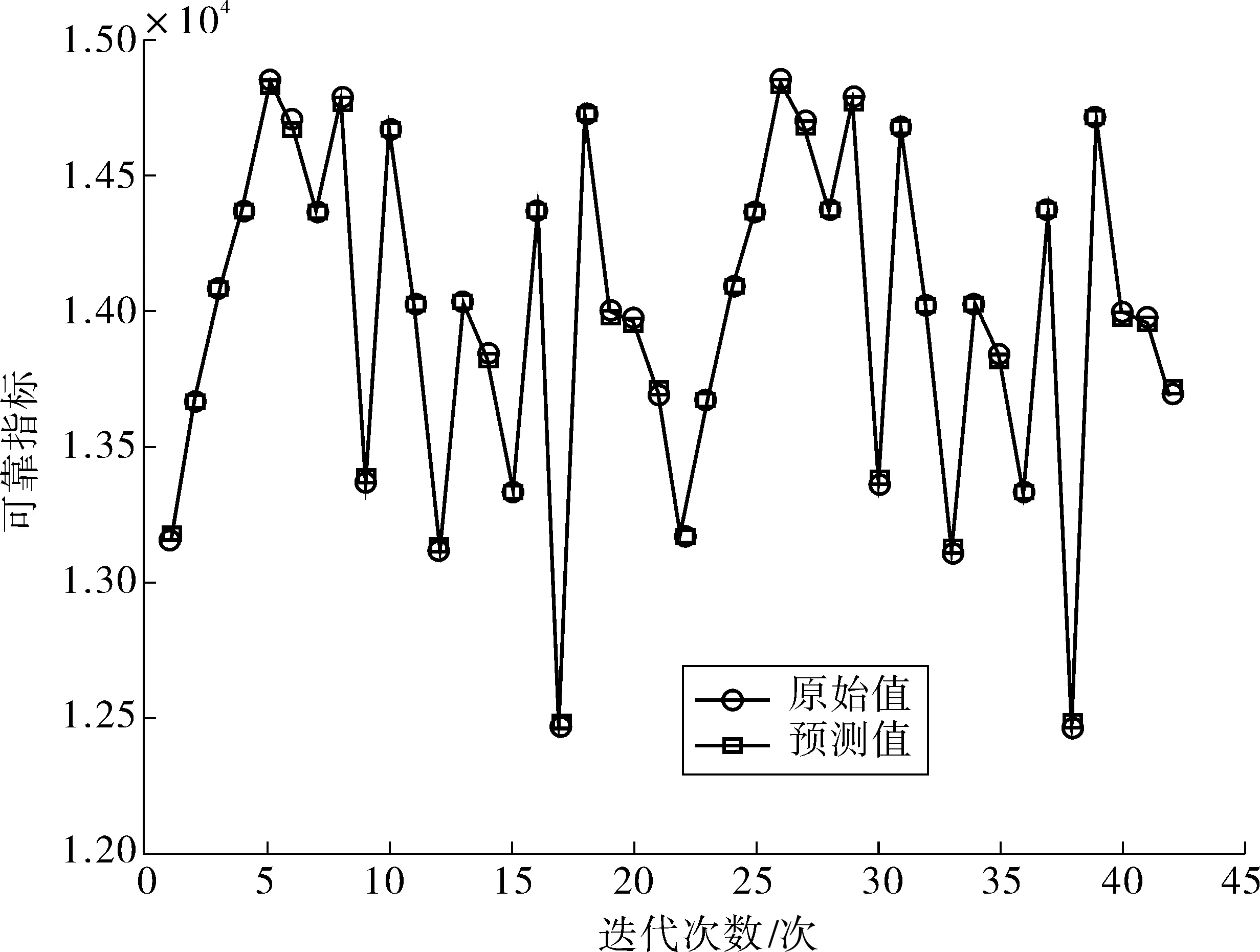
图5 旧梁1的迭代拟合效果
5.3 荷载效应隐式函数预测效果分析
基于支持向量机法构建隐式函数后,需分析该隐式函数对样本数据以外的参数预测效果是否符合工程精度要求。参考文献[19],仅考虑主要荷载工况和小样本条件下,左边跨跨中荷载效应组合(SG+SQ+Sp2)预测偏小,误差范围为-2.07% ~ -2.37%,符合工程精度±5%的要求。针对Ssc贡献比率分析,笔者认为基于RBF-SVM法的对含收缩徐变的拼宽梁桥的隐式函数回归精度理想。
6 考虑时变因素的拼宽T梁桥可靠度计算及分析
结合支持向量法拟合的荷载效应隐式函数S,构建结构抗弯功能函数Z=R-S,并通过MC法求解结构可靠指标。为计算简便,根据结构的对称性[3],仅选择部分梁片来计算各时变阶段(旧梁运营时间+新梁运营时间)的结构可靠指标。
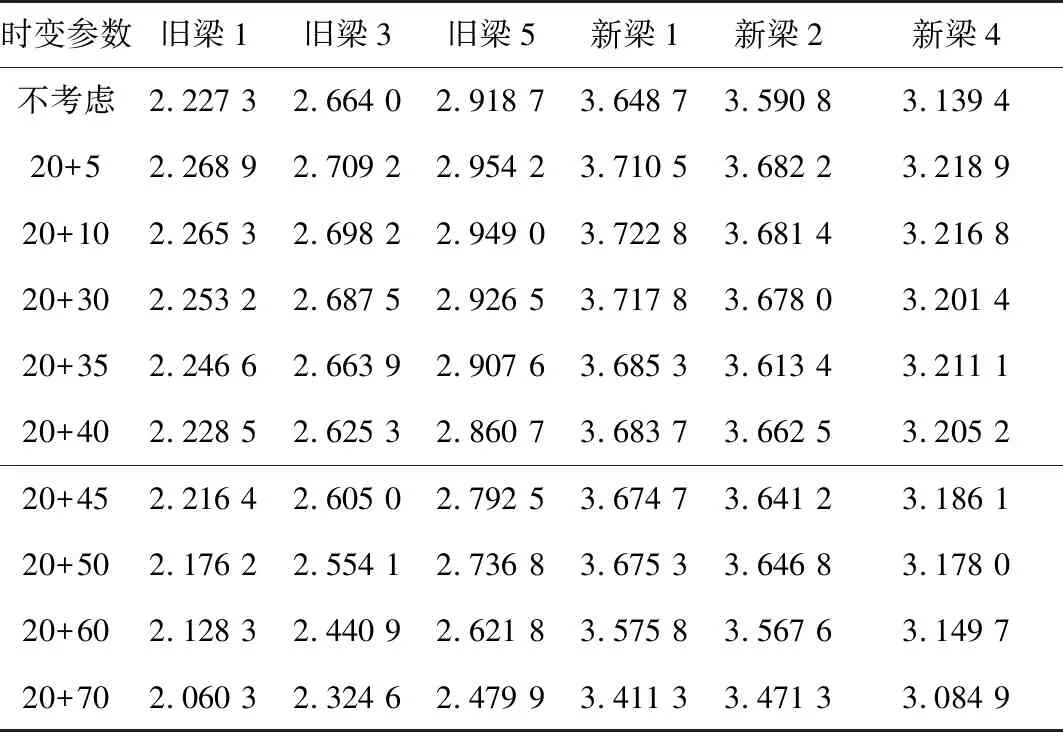
表3 考虑新旧梁运营时间的部分梁片结构可靠指标
旧桥假设已经运营20 a。为方便整体性分析,将6个梁片可靠指标绘成图6。由图6可知:分析时变效应时,新梁可靠指标仍高于旧梁; 分析运营时间时,新旧梁运营时间在70 a前,其结构可靠指标与不分析时变效应时差异不显著; 新旧梁片结构可靠指标总体上高于JCSS(高安全水平下的目标可靠指标JCSS,JCSS=2.3);新旧梁运营70~90 a内,除旧梁1外,其他旧桥边梁附近的梁片可靠指标均满足JCSS要求,而新梁的可靠指标总体上高于JCSS;分析时变效应影响,建议关注旧桥边梁附近的梁片刚度。

图6 考虑新旧梁运营时间的部分梁片结构可靠指标变化情况
单独对各梁片进行时变可靠指标的分析时,如图7:以不考虑时变效应的可靠指标为基准,在旧梁运营70 a内,旧梁可靠指标减少较为平缓,与不考虑时变效应时的可靠指标相近;在旧梁运营70 a后,旧梁可靠指标减少显著,并低于不考虑时变效应时可靠指标;新梁运营50 a内,新梁可靠指标减少较为平缓,并与不考虑时变效应时结构可靠指标相近;在新梁运营50 a后,新梁可靠指标减少显著,并低于不考虑时变效应时可靠指标。
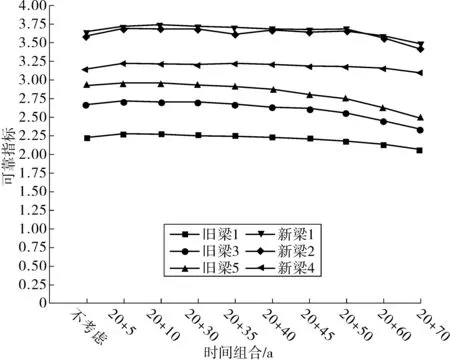
图7 不考虑新旧梁运营时间的部分梁片结构可靠指标变化情况
研究对象为装配式梁桥,因此将新旧梁片简化为任一梁片失效即结构体系失效的串联体系[3,5,21],并采用窄边界法进行结构体系的可靠指标计算。包含钢束二次力效应和收缩徐变的左边跨跨中截面处的体系可靠指标计算结果如图8。假设旧梁运营20 a后进行拼宽,通过对拼宽桥的体系可靠指变化可知:运营时间与拼宽桥体系可靠度呈负相关; 新梁运营45 a内,拼宽桥体系可靠指标降低平缓,超过45 a,拼宽桥体系可靠指标降低明显; 与不分析时变效应的体系可靠指标对比,新梁运营时间在40 a内,体系可靠指标高于不分析时变效应,超过45 a,体系可靠指标低于不分析时变效应。
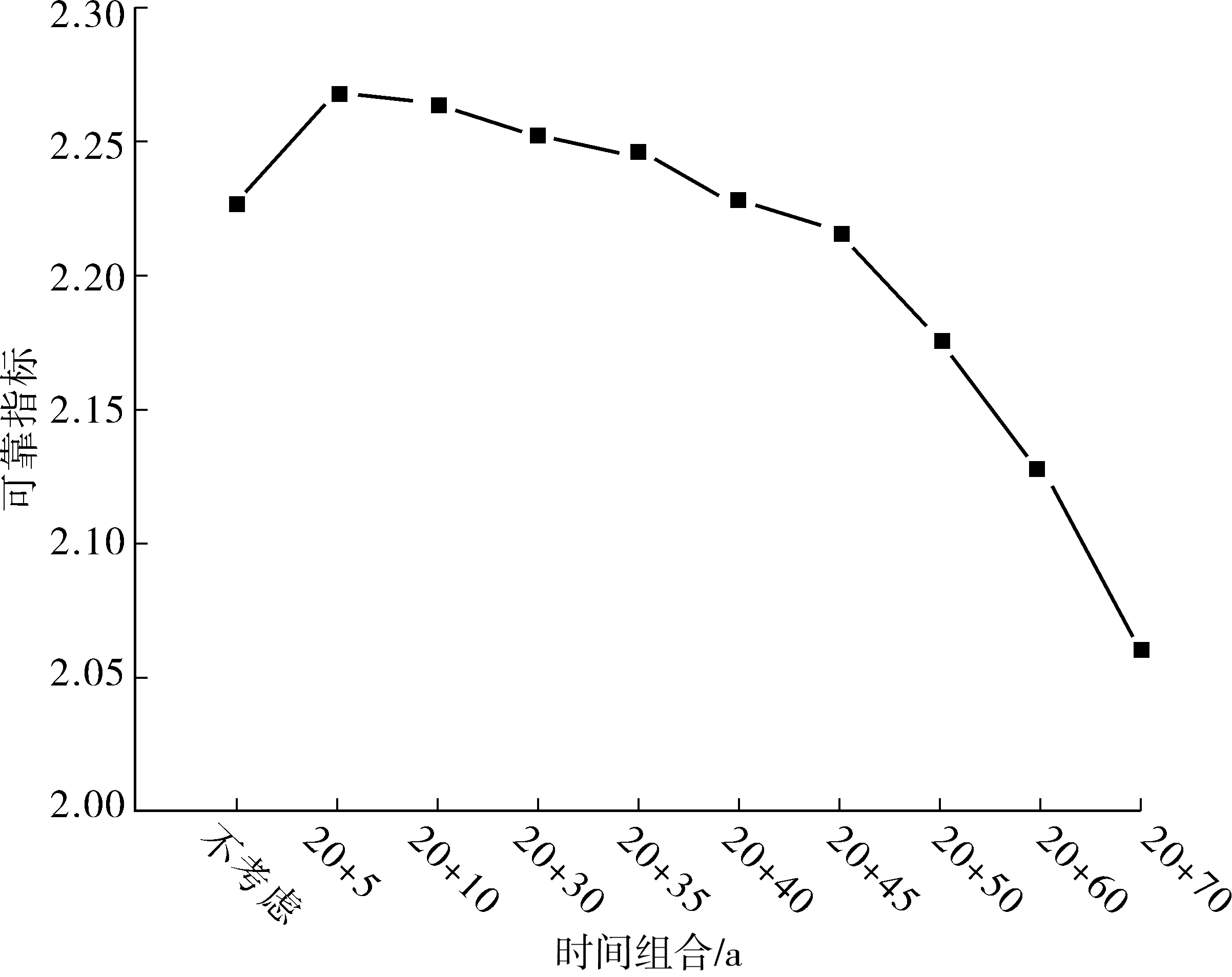
图8 考虑混凝土时变的左边跨截面处体系可靠指标
7 结 论
通过对小样本条件下的荷载效应值拟合效果分析,证明了SVM法可用于桥梁可靠度研究的隐式函数,并研究了混凝土强度和收缩徐变等时变效应对拼宽桥可靠度影响。研究结论如下:
1)通过对考虑混凝土轴心抗压强度和收缩徐变等时变效应分析,随着拼宽桥运营时间增加,拼宽桥的结构体系可靠度逐渐下降:龄期在70 a内,梁片的可靠指标减少并不明显;龄期在70 a后,梁片的可靠指标减少明显。对于拼宽梁桥,在运营后期,应关注旧桥时变效应对体系可靠度影响。
2)与不分析变效应的体系可靠指标对比,且无有害介质侵入情况下,新梁运营40 a内,结构体系可靠指标高于不考虑时变效应;新梁运营时间超过45 a时,结构体系可靠指标低于不考虑时变效应。
