手指静脉图像分形特征提取方法

杨金锋，李乾司茂，贾桂敏

（中国民航大学天津市智能信号与图像处理重点实验室，天津 300300）

近年来，生物特征识别技术成为身份鉴别方法的一个核心研究方向。手指静脉因其具有唯一性、普遍性、稳定性和可度量性以及天然的防伪性和活体性等特点，成为极具应用前景和研究价值的一种生物特征[1-5]。

手指静脉成像利用近红外光（NIR,near-infrared radiation）在手指静脉及其周围肌肉组织中形成的光吸收差异来成像。在没有荧光剂的情况下，所获得的手指静脉图像质量较低。造成图像质量低下的原因有：骨骼和肌肉厚度不同产生的图像阴影；皮肤表面受可见光影响形成的干涉纹理；光线不均匀，大面积的暗明区域使得静脉和背景之间的对比度不高等。这些客观原因直接造成两种重要的成像缺陷：①静脉图像的退化性模糊；②静脉血管网络的局部性残缺。其中，图像退化性模糊可采用传统图像复原技术来处理，而局部残缺问题却无法得到解决，因为生物组织的高散射效应直接造成细小血管无法成像。从识别角度看，决定特征唯一性的恰好是其具有独特性和复杂性的血管网络结构。但目前指静脉识别研究中，在像素层或特征层都没有从血管内在生成机理和复杂网络结构的角度进行深入探究。从学科交叉的角度，关注血管结构本身，从根源上探索指静脉识别问题是有价值的。

自然界中大量存在一种普遍又特殊的几何结构，即树状分叉结构[6]。近年来，相关学者将分形几何理论作为研究这类复杂结构的理论工具，对血管网的结构特征、血液动力学功能、肿瘤血管生成及肿瘤内物质输运等问题都进行了大量定量描述及测量工作，提出了血管网、肺气道、神经网、大脑的褶皱等人体器官结构的数学仿真模型[7-9]。

由于手部血管病变较少，目前尚无针对手部、特别是手指静脉血管网络的分形模拟研究，因此对指静脉图像进行分形特征研究十分必要。常用的分形特征有分维数、分叉角度、分支血管长度、分叉层数、相似性基本单元等。提取指静脉血管网络分形特征对研究指静脉血管复杂结构有重要意义，并为指静脉识别和网络模型重建奠定基础。

1 指静脉分形特征提取流程框架

指静脉原图首先经过滤波、增强、二值化等预处理，采用计盒维数法提取网络的分维数。其次提出一种基于二叉树模型的指静脉图像分形特征提取方法，获取网络结构的分叉角度、血管长度、分叉层数，分析提取到的所有分形特征，结合已有研究数据，得到指静脉图像的分形特征统计结果，如图1所示。

图1 分形特征提取流程图Fig.1 Fractal feature extraction flowchart

1.1 图像增强

在提取分形特征之前，首先要获取足够稳定的指静脉主干网络结构。对手指静脉图像进行预处理，指静脉原始图像（如图2（a）所示）经过背景消除、直方图均衡、中值滤波、归一化（简称滤波）等处理后，主干血管区域已依稀可见，但受大量噪声的影响，血管边缘仍不够清晰，如图2（b）所示。为进一步增强指静脉图像血管形态特征，利用静脉具有的方向性特征，采用基于8方向Gabor滤波器的手指静脉图像增强算法[10]对图像进行增强处理，单尺度多方向Gabor滤波器组为

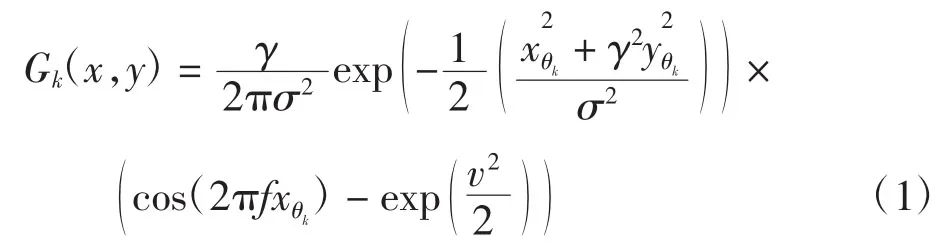
采用3尺度8方向的Gabor滤波器组对指静脉图像进行增强，以获取稳定的主干血管网络，如图2（c）所示，将获取到的血管主干网络部分作为研究指静脉血管分形特征的对象。选取合适的σ值以获得单尺度下的图像增强结果，所得单尺度下较为复杂的血管网络如图 2（d）所示。

图2 预处理中的图像增强Fig.2 Preprocessing image enhancement results

1.2 图像二值化、边缘提取及细化处理

利用多阈值分割算法[11]，对增强后的图像进行分割和二值化处理，结果如图3所示。分割后的二值图像存在虚假静脉结构及孔洞，导致细化后的血管结构出现较多毛刺，不利于后期图像处理。故在细化处理之前先对分割结果去除噪声、填充孔洞、平滑处理。其中，采用Canny边缘检测算法求得血管边缘图像，并采用Hildtich算法[12]细化处理，获得理想的单像素宽度手指静脉骨架结构。

图3 图像二值化、边缘提取及细化结果Fig.3 Image binarization,edge extraction and thinning results

2 分形维数特征提取

2.1 基于图像的指静脉分维数提取

指静脉网络结构具有分形统计自相似的特点，测算指静脉网络的分维数用以描述整个网络的复杂程度，并将其作为后续指静脉建模工作的一个重要约束条件。选用3个指静脉图像数据库作为研究对象：数据库A采集较早，包含585类样本，每类10张，共5 850张指静脉图像，图像尺寸归一化后的像素大小为91×200；数据库B选用山东大学自建库的100类指静脉图像，利用文献[13-15]中的算法得到对应的指静脉ROI图像，每类6张，共600张，尺寸归一化后的像素大小为116×206；数据库C为实验室最新研发的装置所采集，共1 000张指静脉图像，每类10张，尺寸统一为80×160。

首先，基于图像数据库A（随机选取100类）和B比较计盒维数法、sandbox法[16-17]以及分形布朗随机场模型法（FBM，fractional Brownian motion）在指静脉图像上的分维特征提取的稳定性，分别计算3种方法所测分维数据的类内和类间均方差。类内方差越小，则该方法的稳定性越好；类间方差越大，则该方法的区分性越好。由图4（a）和4（b）可知，计盒维数法最为稳定，类内数据波动最小，均方差数值小于0.05，sandbox法的稳定性最弱。为进一步比较，计算2个图像数据库的类间方差，结果如图4（c）和4（d）所示。并随机挑选图像数据库A中的1张指静脉图像进行预处理，计算3个方法下不同预处理结果的分维数。

结合类内和类间对比结果，发现2个不同图像数据库中，计盒维数法和分形布朗随机场模型法均较为稳定，sandbox法下的数据较为散乱，稳定性较弱。不考虑区分性，并综合表1所列单张图片的平均耗时数据，最终选择耗时短且稳定性强的计盒维数法作为指静脉血管网络分维数提取方法，以此作为指静脉模型重建的约束条件。下面对主干血管网络和复杂血管网络进行计盒维数提取以及分维数据统计分析。

2.2 分维特征统计分析结果

分维数作为指静脉血管网络的全局性生长参数，对描述网络复杂度起着重要作用，通过研究指静脉血管网络从主干生长至复杂网络的分维数变化范围，用以控制网络生长的层数。以下分别从血管网络的统一性和特异性角度分析A、B、C 3个指静脉库的分维特征。

观察图5（a），从统一性的角度可明显看出，3个库在复杂血管网络下的分维数都分别大于各自主干网络的分维数。这一结果验证了网络越复杂，层级分支发育程度越高，分维数就越大。对比主干网络和复杂网络的计盒维数结果，随着网络复杂度的提高，其分维数波动幅度大幅减小。说明基于主干网络测算的分维数据，类间的差异性更强。而从特异性角度来看，图5（b）中各数据库的类内差值也不同。3个库的数据值均较为分散，说明就个体而言，血管网络的分化复杂程度也存在差异。统计主干和复杂网络的计盒维数差值，其均值区间在[0.07，0.19]内，可作为基于主干血管网络重建复原迭代层数的数据参考，描述主干和复原后的复杂血管网络相差的血管细节信息，即细小血管重建复杂程度的上下限，可看作统计差异，即血管密集生长的程度和分形级别的差异。分维数作为其中一个重要参数，控制血管的生长限度。

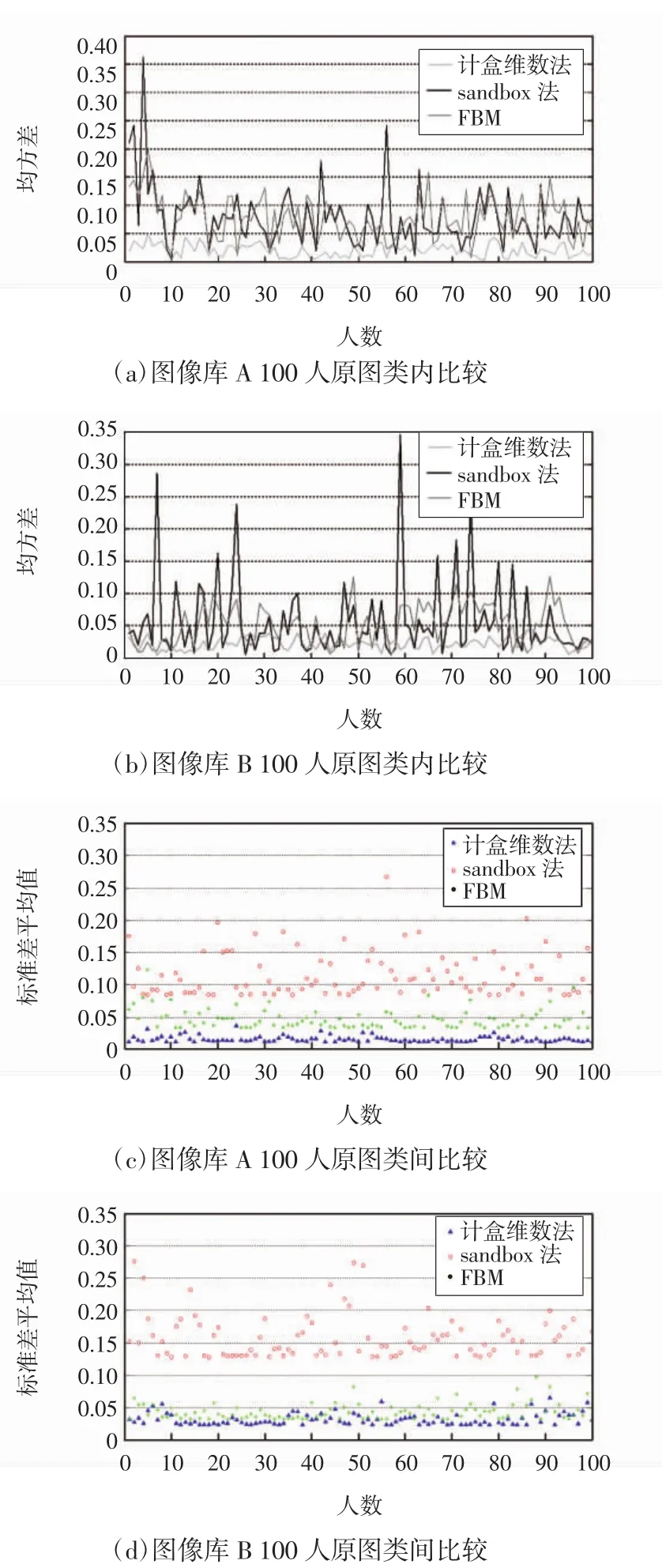
图4 不同库下的分维数提取方法对比实验Fig.4 Experiments of fractal dimension calculation methods under different libraries

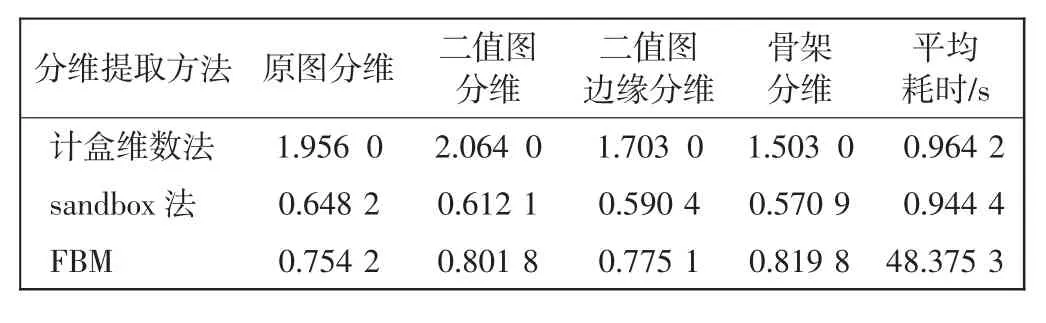
表1 单张图片的3种分维数测算方法对比实验Tab.1 Contrast experiment of three kinds of fractal dimension calculation methods with one picture

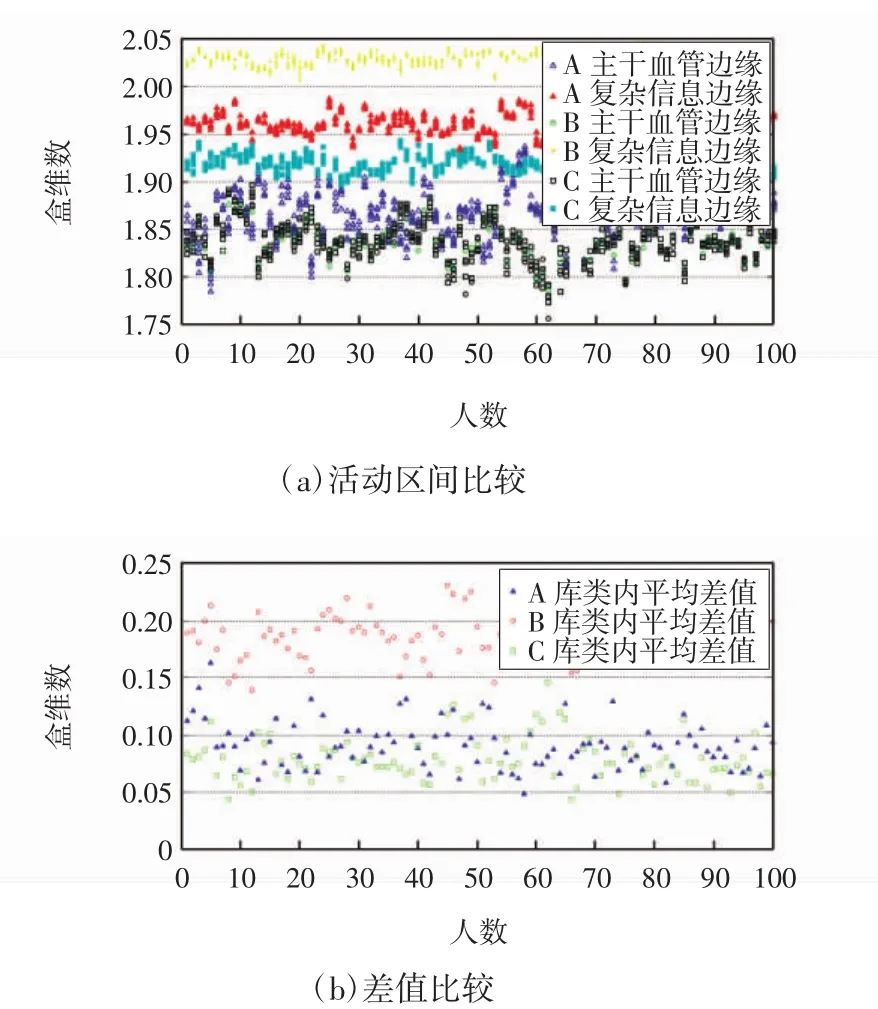
图5 不同库下边缘图层计盒维数比较Fig.5 Box dimension comparison under different libraries

3 基于二叉树模型的分形几何特征提取

3.1 二叉树模型

以上分析了网络的整体复杂度，以分维数作为重建指静脉网络的一个约束条件。但仅由分维数描述血管网络是不够的，还需利用网络的结构特征来更为全面、准确地描述血管。血管所具有的分叉结构是一种高度结合个体差异性和种类统一性的结构。而二叉树结构是树状分叉结构中最典型的一种模式，可以充分描述手指静脉各个分支的空间分布和相互连接关系[18]。结合血管网络骨架的基本形态特征，提出基于指静脉图像的二叉树模型，用于提取指静脉网络的分形几何结构特征。手指静脉网络结构比较复杂，包含大量特征信息，其中的血管段是指细节点之间的曲线段[19]。首先采用文献[11]中的细节点提取方法获取网络结构中的二分叉点和端点信息，然后找出与所有二分叉点相关联的血管曲线段，并将血管段信息进行有序分类和标记，得到此结构的二叉树模型。模型描述了整个血管网络的结构，为后续分形特征提取做好理论准备。

自20世纪以来,人类一直梦想能够设计出代替手工劳动的各种机械臂.自动化技术的蓬勃发展使得人类梦想变为现实.机械臂的发展涉及多种学科,包括机械、电路控制、计算机及仿生学等.目前,机械臂的驱动方式包括气动驱动、电动机驱动和液压驱动等[1].气动驱动方式成本较低、维护方便、质量轻,但是轨迹跟踪精度低;电动机驱动方式体积较小、结构简单、价格较低,但是功率质量比不足;液压驱动方式具有运动精度高、功率质量比大、传递负荷和环境适应能力较强等特点.因此,机械臂驱动方式大多采用液压驱动,从而掀起了设计者对机械臂液压驱动方式研究热潮.

如图6所示，选取端点（正方形框处）和二分叉点（三角形框处）作为研究对象。通过观察血管结构，将图像中的血管类型简单分为两类：①连通区块具有至少1个二分叉点的血管区域；②浮游区块由2个端点为血管曲线段端点的血管区域。

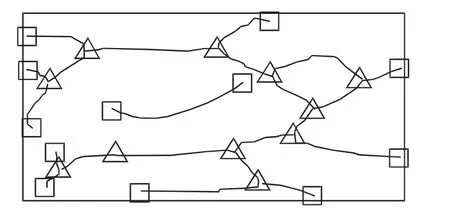
图6 指静脉图像的细节点提取Fig.6 Minutiae extraction of fingerprint images

对于血管连通区块，以二分叉点作为曲线段追踪的出发点，最终找出以此分叉点建立相关连接的3条血管曲线段，并构成一个二叉树单元。一幅图像中单元的个数等同于二分叉点的个数，这样便将血管网络以二叉树单元的方式进行存储。人体末端组织血管分支总是呈现细长的形态特征[20]，指静脉血管的生长方向为腕端向指端，设定曲线段追踪核函数为固定值[8 5 4；9 1 2；7 6 3]，如图 7 中间模块所示，此核函数代表曲线段追踪的顺序，计算结果越大越优先。假设p为任意一个二分叉点，如图7左侧模块所示，中心点周围所有值为1的点就是追踪的目标点，按照右侧模块的计算结果，从小到大依次进行曲线段追踪，将目标点作为待处理点再次进行判断和追踪，直到目标点为二分叉点或端点追踪结束。对其进行优先排序，是为了定义父子血管关系。二叉树单元的提取结果分别由3 段血管曲线段信息组成，记为 chain1，chain2，chain3。

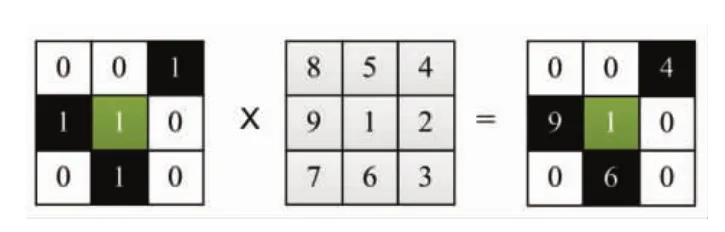
图7 基于二分叉点的曲线段追踪Fig.7 Curve segment tracing based on bifurcation point

对图6中每个分叉点进行二叉树单元信息存储，将获得的所有曲线段信息记为二叉树单元链路矩阵C。然而对于血管浮游区块，需要进行单独的曲线段追踪和存储。血管连通性越好，矩阵C的信息就越丰富，用于表达结构特征的关联信息也就越多。每个分叉点对应1个父子层级关系，利用上文所定义的追踪核函数，结合3条血管曲线段之间的夹角大小关系，定义二叉树单元的父子血管层级关系：形成的最小夹角所对应的3条曲线段中若出现标记为chain1的血管，则所对应的两条曲线段为“父血管”，记为“0”；反之，对应的这两条曲线段同时为“子血管”，记为“1”，这个过程称为父子标记。对各个二分叉点下的曲线段进行父子标记便可得到二叉树单元父子层级关系矩阵L。图6中二叉树单元的父子层级关系矩阵L如表2所示。

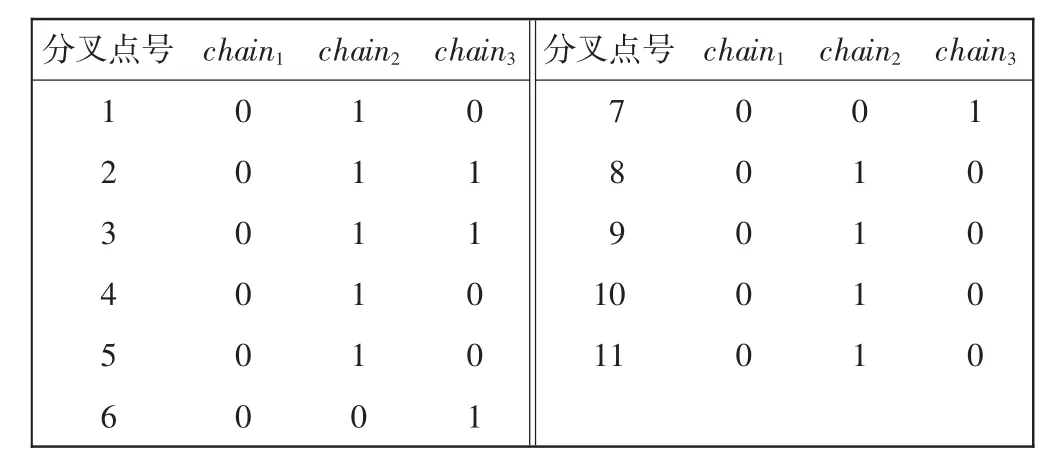
表2 血管父子层级关系矩阵LTab.2 Vascular hierarchical relationship matrix L

3.2 基于二叉树模型的分形特征提取

利用3.1节所提出的二叉树模型，分析指静脉网络结构特征，提取血管结构中的血管分叉角度、血管长度以及分叉层数，并进行特征标记，统计分析数据，得到血管结构分形特征的规律。

1）提取分叉角度 以二分叉点为中心，向外发散的3条血管曲线段之间的交叉角度称之为分叉角度。根据生物流体力学模型，可以定义基于二分叉点的由血管曲线段所形成的最小血管夹角，称之为此二叉树单元的血管分叉角度，并选取该角度作为夹角统计分析的初始数据。

2）提取血管长度 血管曲线段的长短，即总共包含的像素点数，表征了血管的长度。提取所有血管段的像素数表征其血管长度。

3）提取分叉层数 结合二叉树单元父子层级关系矩阵L和二叉树单元链路矩阵C中的信息，提取包含整个网络的层级信息，可对整个血管骨架网络进行准确的描述。在矩阵C中，两端都为分叉点的曲线段信息会被同时记录2次并存储于不同的二叉树单元中，通过在矩阵C中找到这些共有曲线段，并对其进行关联标记，可获得一个较为完整的父子层级数据矩阵LN。步骤如下：

第1步区分连通区域并标记二分叉点。将二分叉点按照不同的血管连通区域进行分类，通过父子标记得到各二分叉点之间的父子层级关系，获得带有区域标记的矩阵C和二叉树单元父子层级关系矩阵L；

第2步获取同曲线段位置对矩阵SL。对矩阵C进行血管段类型判断，找出两端均为二分叉点的曲线段，相应找出此条曲线段在矩阵C中的位置对，并按照顺序赋值进行位置对匹配标记，遍历所有二叉树单元最终得到位置对矩阵SL；

第3步提取整个网络的血管分叉层级矩阵LN。结合矩阵L和SL，借助深度遍历思想，按照区域顺序判断同曲线段位置对关联的所有二叉树单元之间的关系。假设某网络的第1个二叉树单元父子层级数据为[011]，其中chain3为同曲线段，层级为1。且其所对应的另一个二叉树单元的数据为 [0 0 1]，对应的同曲线段为chain1，则将层级1赋值给关联二叉树单元的chain1，并进行相对应的层级赋值结果为[1 1 2]。依此层级遍历法，即可提取整个网络的血管分叉层数，称为LN。

以上实现了基于二叉树模型的指静脉网络结构分形几何特征提取。在此基础上，将每个样本所提取到的血管分叉角度、血管长度、分叉层数，利用K-means获取每种特征的聚类中心及其在该血管网络中出现的概率，某一指静脉网络的分形特征经过聚类后的结果，如表3所示。

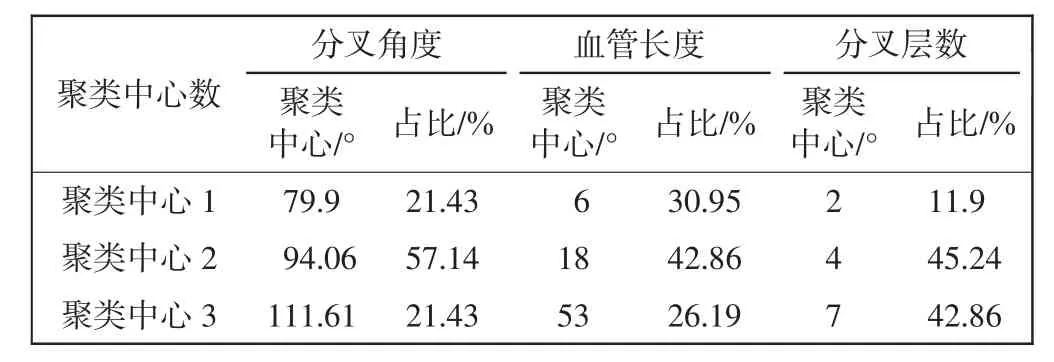
表3 K-means聚类结果Tab.3 K-means clustering results

3.3 分形特征分析

为研究数据库中每类指静脉图像的血管分叉角度、血管长度和分叉层数特征的类间特异性，运用K-means对每类图像的分形几何特征进行区间聚类，分别统计各分形几何特征在其各聚类区间的占比，并据此选择血管重建参数，如表4所示。

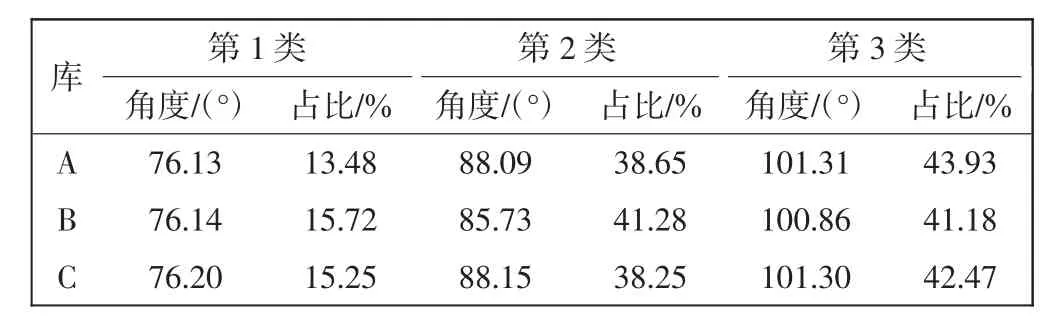
表4 不同库的分叉角度聚类结果Tab.4 Bifurcation angle clustering results of different libraries

由表4可知，不同库之间的分叉角度聚类结果相差并不大，85°～100°的夹角占比较大，为85%。通过数据集聚类，稳定分叉角度范围在[85°，100°]。将该结果与医学研究结果[75°，90°]比对，发现结果整体上升，原因在于测量的分形特征是基于图像像素层的结果。

结合分维数统计结果可知，手指静脉网络的分维数和分叉角度相对稳定，可将分维数作为全局控制参数制约网络重建的迭代层数，并将分叉角度稳定在[85°，100°]，在重建时用以控制血管长势。

同样地，针对血管长度和分叉层数进行聚类。如表5所示，处于第3类的血管链路占比较大，这与血管曲线段分化复杂度相关。且由于实验所选取的图像数据库均只有指静脉ROI区域，其首级父血管和末级子血管被截断，测得的分形特征不能完整地表达整个手指静脉网结构特征。但仅基于图像来讲，一定程度上表达了静脉结构的分形特征。

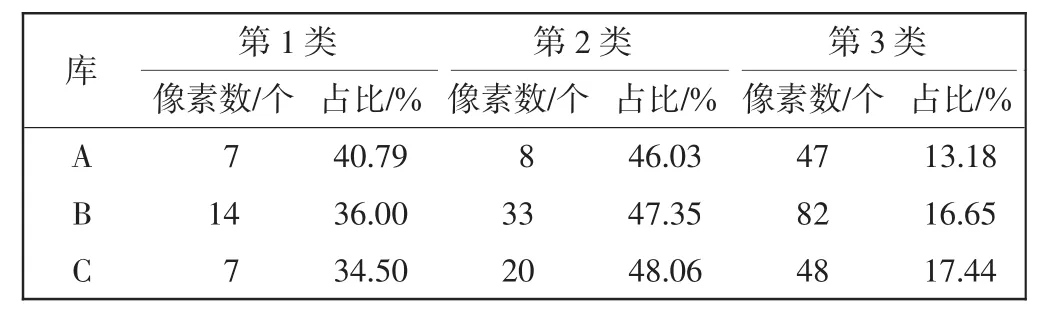
表5 不同库的血管长度聚类结果Tab.5 Vascular length clustering results of different libraries

观察表6，基于图像的静脉血管网络分叉层数变化越符合逐级递增，越能够体现网络的完整性和生长良好性。而网络在某一层级存在大量同级血管，其他级别的血管很少，说明网络完整性被破坏。通常来讲，这种网络能够被利用的有用分形信息较少。重建此类网络需同时结合其他分形特征来进行残缺复原和重构。

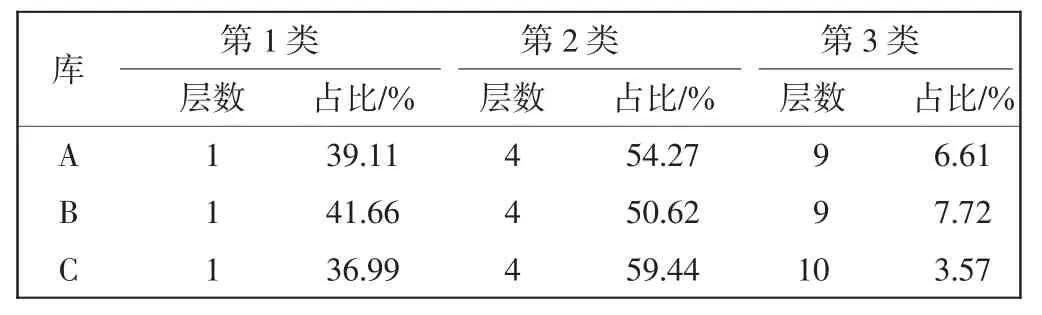
表6 不同库的分叉层数聚类效果Tab.6 Bifurcation layer number clustering results of different libraries

4 结语

首先对指静脉主干网络结构进行多种分维数测算方法的对比实验，选择计盒维数法提取分维数特征，从全局上对血管网络复杂度进行描述，提供了指静脉血管主干网络到复杂网络生长的数据。其次提出一种基于二叉树模型的分形几何特征提取方法，实现了网络的血管分叉角度、血管长度和分叉层数特征提取，并利用K-means获取每种特征的聚类中心及其在该血管网络中出现的概率，较为准确地描述了血管网络的结构特征。实验所提取到的分形特征可为指静脉网络模型提供基础数据，从而解决血管网络局部残缺问题，有利于提高指静脉图像识别精度。

但此分形特征提取方法和实验都仍有改进空间，为了更加准确地分析和提取血管网络的分形特征，需采集全手指的图像库，提供进一步利用更多的指静脉分形特征信息，实现指静脉血管网络重建。