Kramers-Kronig关系的研究与发展
2019-05-13阎春生
阎春生
(1.浙江大学 图书馆,浙江 杭州 310058;2.浙江大学 光电科学与工程学院,浙江 杭州 310058)
1 KK关系的提出
KK关系指的是响应函数的实部与虚部之间的一种数学关系,自从Kronig(1926)[1]和Kramers(1927)[2]利用原子气体模型推导出来以后,它就在光学、材料、非线性、通信等领域得到了广泛而重要的应用。KK关系的独特魅力在于,虽然它原始的推导基于具体的物理模型,或者是基于信号的线性、因果性和无限频率下对激励的响应为0这样的物理实在,但它的确可以不依赖于任何模型而存在,它的美在于它纯粹的数学性之中蕴含的应用的普适性,这是两位提出者始料未及的[3]。
2 KK关系的本质
KK关系本质上是希尔伯特变换的一个特例。
2.1 希尔伯特变换[4]
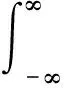
2.2 KK关系本质上是具有因果关系的平方可积函数的希尔伯特变换
对于解析函数,即任何具有因果关系的平方可积L2函数a(x)而言,希尔伯特变换便演化为KK关系,它揭示了其傅立叶变换a(x)=u(x)+iv(x)实部和虚部之间数学上的内在联系[6],即:
(1)

(2)
此处P为柯西主值积分,其积分区域是将被积函数的极点x′用极小的半圆去除后形成的,图1中除了该点以外整个的上半复平面(带实轴)。
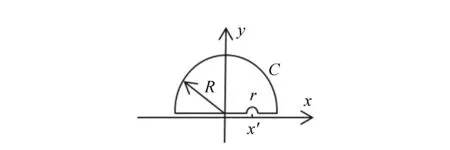
图1 公式(1)的积分区域(R→∞,r→0)Fig.1 Integral region of formula 1(R→∞,r→0)
若a(t)是实函数,则a(-x)=a*(x),*号为复共轭,因此a(x)的实部是偶函数,虚部是奇函数,这在量子力学散射问题中称为交叉条件。上述条件赋予了函数a(t)和a(x)重要的物理意义,例如a(t)代表系统的时域响应,a(x)代表其频率响应,若将x用频率ω代替可得[7]:

(3)

(4)
2.3 因果关系的两层涵义[8]
因果性或因果关系是KK关系的基石,一般有两层涵义,前者具有更普遍的意义。
(1)原始因果性:结果不能超前于原因,即t<0时,a(t)=0;
(2)相对论因果性:任何信号的传播速度都不能超过光速。
3 超收敛定理和求和规则[6,9-10]
KK关系涉及到了∞的积分,为了研究柯西积分函数在无穷远处的渐近行为,引入超收敛定理以及f求和规则。
3.1 超收敛定理
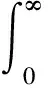
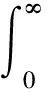
(5)
3.2 f求和规则
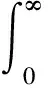
(6)

4 介质的线性KK关系
4.1 响应函数
4.1.1 反射谱
通常通过测量垂直入射光反射估计高吸收样品(如金属、薄膜、半导体等)的光学常数,其反射谱为r(ω)=|r(ω)|eiθ(ω),或ln[r(ω)]=ln|r(ω)|+iθ(ω),|r(ω)|为振幅,R(ω)=|r(ω)|2为反射光强度,θ(ω)为相移,KK关系可以表示为[12]:
(7)

(8)

(9)
其中,式(8)[13-15]又称为微分KK关系;式(9)[16-17]增加了ln|r(ω)|项,保证被积函数总是有限的。
实验测得反射率R(ω)或其振幅|r(ω)|,由公式(7)到(9)计算出相位θ(ω),根据菲涅尔公式r(ω)=[(ω)-1]/[(ω)+1],就可以计算出复折射率=n+iκ,n和κ分别为折射率和消光系数。
4.1.2 透射谱
对于透射光谱,还需要考虑光在介质中传输产生的相移,KK关系修正为[18]:
(10)
其中,T为透射谱函数的振幅,d为厚度。
4.2 电学特性参数
4.2.1 复极化率和复介电常数
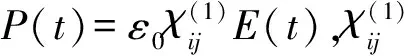
4.2.1.1 导体
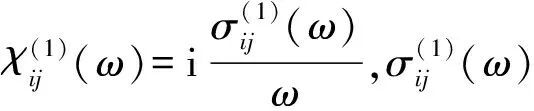
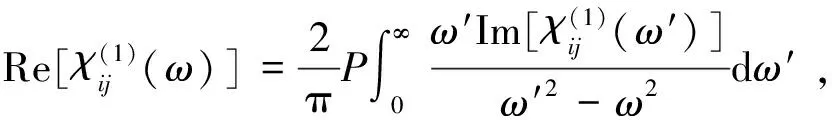
(11)
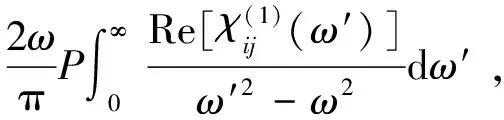
(12)
其中用到了积分变换将(-∞,∞)的积分范围变换到(0,∞):
(13)

(14)
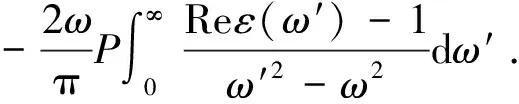
(15)
4.2.1.2 纳米结构
纳米结构[20-21]需要考虑局域场效应对系统哈密顿量的贡献,但并不改变系统格林函数的因果关系,KK关系仍然适用且形式不变。
4.2.1.3 非导电介质

4.2.2 电阻抗
电阻抗Z=Zr+iZj是评测电路、电极、电化学系统的重要参数,Zr代表阻抗,Zj代表电抗,其线性KK关系为[22-24]:
(16)
Zr(ω)-Zr(∞)=
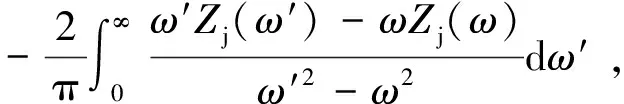
(17)
Zr(ω)-Zr(0)=
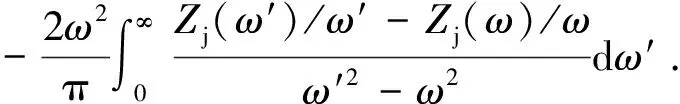
(18)
4.3 磁学特性参数[25-26]
(19)
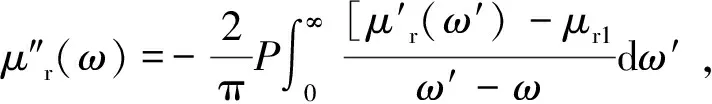
(20)
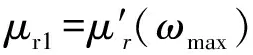
4.4 光学特性参数
4.4.1 复折射率和复介电常数
复折射率从宏观角度描述了光与物质的相互作用,其实部n与光波的相速度vφ=c/n有关,虚部κ一般是正的,代表光的衰减。
4.4.1.1 均匀薄膜或薄板
厚度为L的均匀薄膜或薄板,κ=-c/(2ωL),其KK关系[27]为:
(21)
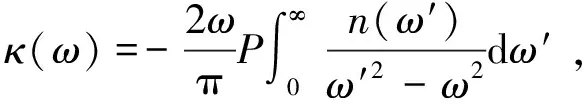
(22)
求和规则为:
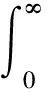
(23)
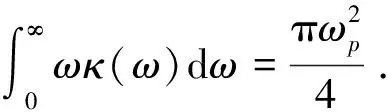
(24)
4.4.1.2 超材料板
厚度为deff、复折射率为Neff的超材料板,其消光系数为κeff=-Re[ln(eiNeffk0deff)]/k0deff,利用式(21)即可确定其有效折射率neff[28]。
4.4.1.3 气体分子
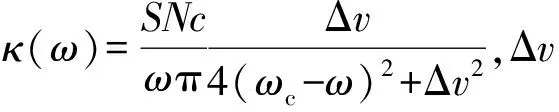
4.4.1.4 负折射率介质
(25)

(26)
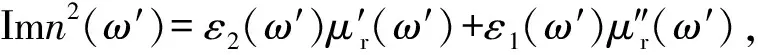
4.4.1.5 增益介质
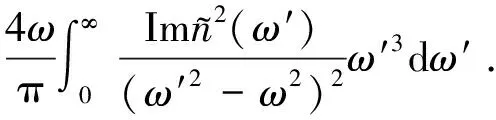
(27)
4.4.2 光电导率
光照引起材料电导变化的现象称为光电导效应,是内光电效应的一种,变化的电导率部分称为光电导率σopt=σ1+iσ2[32],满足线性响应中的Kubo-Greenwood理论[33-34],其KK关系[35]为:
(28)

(29)
4.4.3 X射线的复原子散射因子[36-37]
X射线吸收光谱XAS和近边X射线吸收精细结构NEXAFS测试中,都涉及到极紫外EUV和X射线光谱,其复折射率定义为:
N(ω)=1-δ+iβ=

(30)
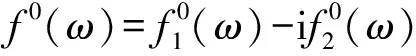
(31)
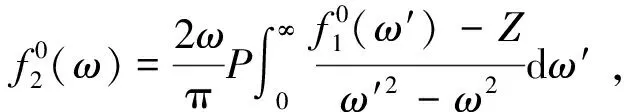
(32)
其中,Z是每原子的电子数。
4.5 声学特性参数
4.5.1 绝热压缩系数
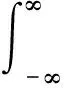
(33)

(34)
其中,k=ω/cp(ω)+iα(ω)是超声波的波数,k2=ω2ρ0K(ω),ρ0是介质的密度,cp(ω)和α(ω)分别是相速度和衰减系数,二者也满足KK关系[40]:
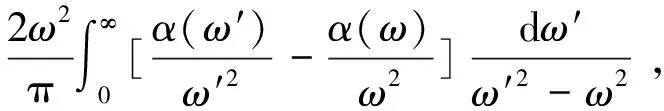
(35)
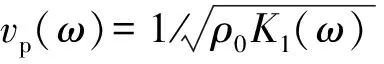
4.5.2 声折射率[41]
声折射率的KK关系与式(25)的形式完全一样。
4.5.3 散射函数[41]
当材料中存在许多尺寸相同各向同性的散射体时,声波的色散关系变为:

(36)
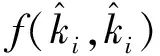
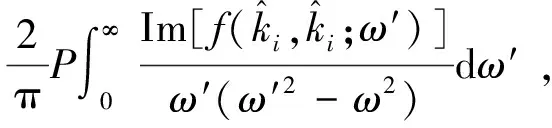
(37)
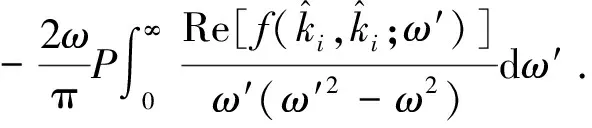
(38)
5 非线性KK关系
当激发场很强时,必须考虑非线性效应[42-43],如和频、差频、四波混频、自相位调制、交叉相位调制、多光子吸收、多次谐波产生、光孤子、拉曼散射、布里渊散射等。
5.1 非线性极化率
5.1.1n阶非线性极化率
5.1.1.1 单变量积分
非线性介质的n阶极化响应为:
(39)
非退化n阶非线性极化率的KK关系为:
χ(n)(ω1,…,ωn)=

(40)
5.1.1.2 多变量积分
对式(40)所有剩余的n-1个频率变量进行同样的运算并应用对称关系可得[44-45]:
(41)

(42)
5.1.2 洛伦兹振荡器模型[46]
5.1.2.1 和频
(43)
当r≤m,[χ(n)]m和(ω1,…,ωn)r×[χ(n)]m也是全纯函数,KK关系为:
(44)

(45)
5.1.2.2 差频
当差频产生时,非线性极化率在复频率平面的上下部分存在极点,为亚纯函数,只要乘以一个函数将相关极点消去可以得到一个全纯函数,即:
(46)
其中,Ωku是极点,v=1,2,…,V。
5.1.3 非导电介质谐波极化场

(47)
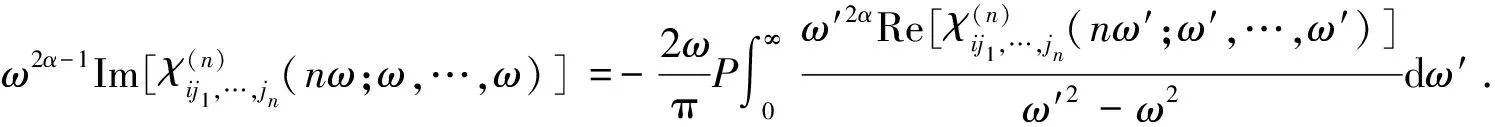
(48)
大频率下至少随ω-2减小的谐波极化率,其α阶矩(0≤α≤n)极化率的k次方的KK关系为[49]:
(49)
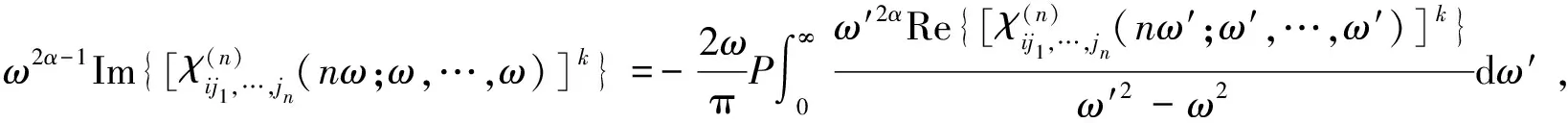
(50)
其中,0≤α≤k(n+1)-1。
5.1.4 导电介质谐波极化场
对于非线性静态非消失实张量,频率趋于0时产生的谐波极化率为:
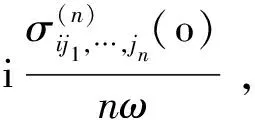
(51)
导电介质谐波产生极化率的非线性KK关系为:
(52)
5.2 折射率及消光系数的变化
5.2.1 泵浦-探测系统
当两个单色平面波入射到非线性介质时,由于频率ωb处光场的存在引起的频率ωa处折射率的改变Δn(ωa;ωb)和吸收系数的改变Δα(ωa;ωb)为:
(53)
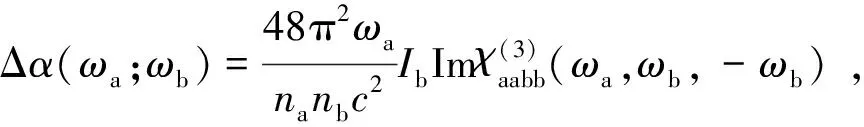
(54)
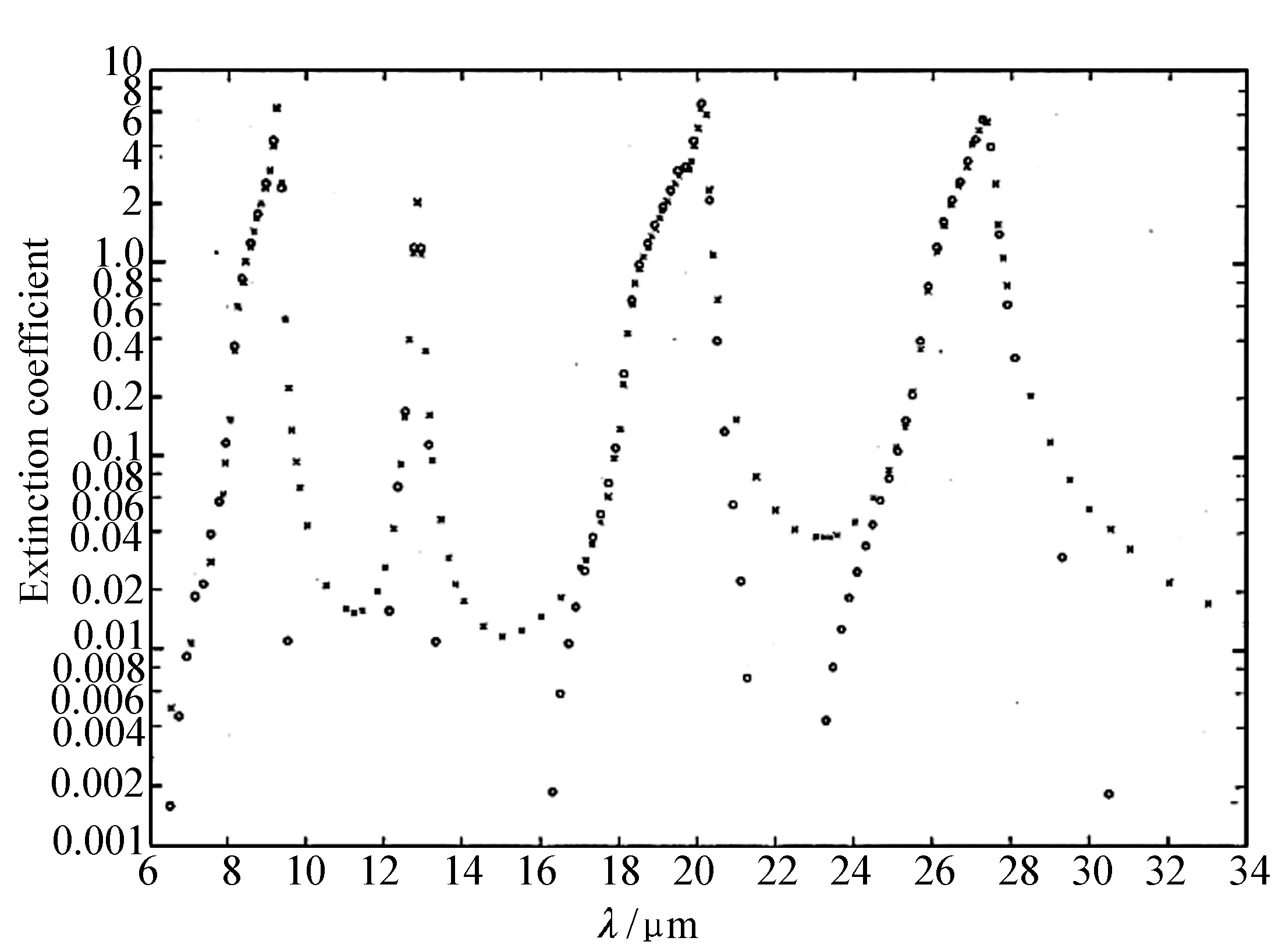
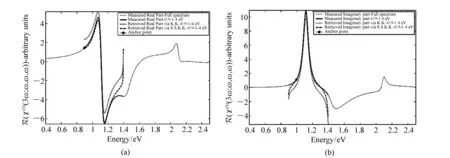
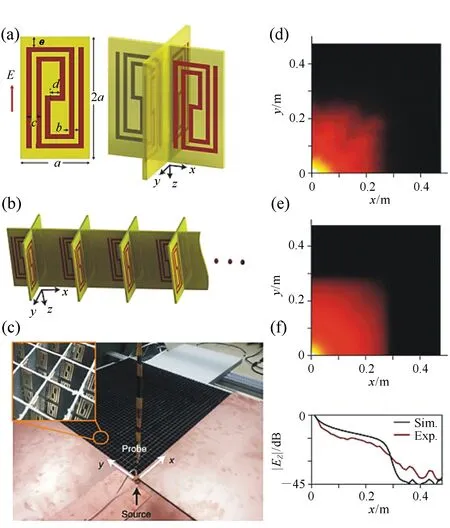
其中,Ib是频率ωb处的光辐照度。na和nb分别是频率ωa和ωb处的线性折射率。假定线性吸收足够小,α(ωa)c/ωa< (55) 上式等价于用频率ωb处固定的强光泵浦和频率ωa处的弱光探测的泵浦-探测光谱。 5.2.2 自作用系统 用光子能量ћω、强度为I的入射辐射泵浦半导体,折射率改变的KK关系为[51-53]: (56) 上式与(55)具有相同的形式,但泵浦或扰动为入射光场自身,因此可以看作一个自作用系统。 5.3.1 三阶 (57) (58) 5.3.2n阶 将其推广到任意维度为[55]: (59) (60) 其中,Ω0=ω1+…+ωn,Ω1=ω1-ω2,…,Ωn-1=ωn-1-ωn。 (61) 将δω(θ)代入上式并考虑其对称性得: (62) (63) (64) 表1列出了几种非线性效应的名称和对应复电导率张量的数学表达式,以及在上半/下半频率平面,对哪个变量(ω、ω1或ω2)解析。 表1 非线性效应及数学形式 KK关系在应用中最大的局限性在于,复变量仅仅在有限的区间而非整个积分限(0,∞)上已知或可测量,比如光谱相对于整个电磁波谱来说几乎是微不足道的,运用介质的吸收光谱来计算KK积分必然带来很大的误差,如何减小截断误差成为重要环节。 (65) (66) Myhre等人[59]研究了硫酸溶液,发现5 000 cm-1的高波数截止对KK计算的吸收和折射率影响很小,而低波数截止如1 600 cm-1以下时,吸收系数误差为3%~50%,折射率误差整个频段小于5%。 Herbina等人[60]研究了石英粒子,发现其消光谱在紫外可见波段(10 000 cm-1, 50 000 cm-1)特别对n敏感,在热红外波段(550 cm-1, 2 000 cm-1)对n和κ同时敏感,如图2所示。 图2 κ(黑点)和n(灰线)的雅克比谱分布[60]Fig.2 Jacobian spectrum distribution of theκ(black dot) andn(grey line)[60] 为了减小KK截断误差,需要对积分限以外的数值进行合理的估算,主要有以下方法。 6.2.1 常数外推法 Gottlieb等人[61]研究了氟化锂的光学特性,将(0,150 cm-1)的反射率设为常数0.24,(3 000 cm-1,∞)的反射率设为常数0.03,该方法虽然简单但会得到负值,并且在一些频率吸收系数严重失真。 6.2.2 多项式外推法 Thomas等人[62]在分析CdS的激子光谱中,用多项式A+Bv+Cv2进行外推,其中A、B和C可由计算机调整以在能量低于吸收边的地方产生零吸收。Spitzer等人[63]研究了石英的红外晶格带,计算了波长5~37 μm共160个点的数据,相角的校正项为Δθ(λ)=-0.022 4-0.018 8(λ/5)+0.061(λ/5)2。κ>0.1时 KK误差在消光峰的短波边较小,在长波边较大,而κ<0.1时误差非常大,如图3所示。 图3 消光谱:×为理论值;○为KK计算值[63]Fig.3 Extinction spectrum:× is theoretical value; ○ is KK calculation value[63] 6.2.3 幂指数外推法 Herbin等人[60]根据色散理论,采用幂指数外推法: (67) 文章结合单减KK关系及最佳估计法进行迭代计算,在紫外-可见波段误差小于1%,在红外振动带附近误差为2%,如图4所示。 图4 (a)和(b)分别是先验和重建的κ和n[60]Fig.4 (a) and (b) are priori and retrieved values ofκandn, respectively[60] 6.2.4 无阻尼谐振子外推法 考虑一个简单的如图5所示的色散曲线,高低频截断误差在A-B和C-D部分有相互抵消的倾向,精心选择可以减小截断误差,当ω/ωmin≈ωmax/ω时,抵消的效果最好。 微分KK关系如(8)式所示[13-15],它引入了一个权重因子,其在极点ω′=ω处有一个尖峰,而远离该点则变得很平很小,使得反射谱强度在每个频点贡献不一样,大大减小了需要积分的范围,极点两边对称的部分也倾向于相互抵消,因此可以有效降低截断误差的影响。常用的复介电常数和复折射率的微分KK关系也可以改写为: 图5 色散曲线[58]Fig.5 Dispersion curve[58] (68) (69) (70) 相比于上述的外推方法,基于锚点的减法KK关系显得更为有效一些。 7.1.1 折射率与消光系数 Bachrach等人[65]在分析法拉第旋光数据的文章中首次提出了单减KK关系[60]: (71) 其中,n(ω0)是锚点ω0处的折射率,为已知值。SKK的优点在于收敛速度快,可以在有限的波段获得相对准确的结果。 7.1.2 反射率与相位 Ahrenkiel[66]提出了反射率和相位的SKK关系: (72) 采用常数外推法,并将ω1处的反射峰用δ函数替代,文章分析了引入未知峰对SKK与KK两种方法计算误差的影响: (73) 当ω~ω0,ω1>ω0时,ΔSKK<ΔKK,并且当反射数据在小范围可知时,SKK比KK收敛更快。 7.1.3 3次及n次谐波非线性极化率 n次谐波的SKK关系为: (74) (75) 如图6所示,Lucarini等人[67]比较了聚硅烷三次谐波非线性极化率的实验测量曲线(实线和延长的点画线)、KK(点)和SKK(线段)计算曲线,可以看出,SKK关系具有较好的重建精度,而KK关系由于截断误差而有较大偏离。 图6 χ(3)(3ω;ω,ω,ω)实部(a)和虚部(b)的测量值,KK和SKK计算值[67]Fig.6 Measured, KK and SKK values ofχ(3)(3ω;ω,ω,ω):(a)the real part; (b)the imaginary part[67] 7.2.1 反射率与相位 Palmer等人[68]1998年在SKK的基础上推导了多减KK(MSKK)公式: (76) 采用常数外推法,假设在波数ωp>ωmax时,存在一个近似为狄拉克δ函数尖锐吸收带,N阶和N-1阶MSKK、KK关系的截断误差分别为ΔN、ΔN-1和Δ0,并有如下关系: (77) (78) 上式说明MSKK比KK关系截断误差小,而且锚点越多理论上截断误差越小。 7.2.2n次谐波非线性极化率 Lucarini等人[67]同样也推导了n次谐波非线性极化率的MSKK关系: (79) (80) 对传递函数ln[H(ω)]=ln[H(ω)]+idθ两边求导,得:dln[H(ω)]/dω=dln[H(ω)]/dω+idθ/dω,求导不改变其因果性,因此也满足KK关系: (81) 差分多减KK关系可以表示为: (82) dθ/dω是时间延迟,因此差分多减KK关系实际上是传递函数幅度的导数与其时间延迟之间的关系。 图7 一维周期介质散射谱相位差重建[69]:实验测量SPEBI方法(实线),KK关系(点画线),DSSKK关系(点),DMSKK(线段)Fig.7 Phase difference reconstruction of one-dimensional periodic dielectric scattering spectrum[69]:experimental measurement SPEBI method(solid line); KK relationship(dash dot); DSSKK relationship(dot); DMSKK relationship(line segment) 从图7可以看出,仅用了两个锚点(1 542.55 nm和1 563.55 nm)的DMSKK方法精度最高,与用相位差光谱测量方法SPEBI实验得到的曲线最逼近,DSSKK(锚点1542.55 nm)次之,而KK方法则无法正确重建相差。 8.1.1 单向无反射空间KK介质 最近Horsley等人提出了一种空域上的KK关系,如果平面介质的非均匀介电常数的空间分布函数ε(x)=εb+α(x)在上或下复空间平面解析,则满足式(83)和式(84)的空间KK关系[71],其中εb>0是假定的背景值,当x→±∞时,其空间变化部分α(x)=0。 (83) (84) 适当选取α(x),可以构建一个无源无反射的电磁吸波介质,这在电磁隐身领域具有重要意义。 无反射介电常数ε的空间函数可以表示为: (85) (86) (87) 其中,ξ设置了介电常数轮廓的空间尺度,A是幅度,式(87)表示一个光滑的三角函数,erf是误差函数,h和L分别是高度和长度,ζ表征角的平滑度。 Longhi指出[72]在考虑空KK介质的散射问题时,需增加一个取消条件[73]: (88) 8.1.2 双向隐身空间KK介质[74] 介质是TM极化波双向隐身的,若满足以下条件之一: (1)α(x)=β(x)exp(iΘx),β(x)在上半复平面全纯,且当|x|→∞时,β(x)→0; (2)ε(x)=εb+α(x)在上半复平面没有零点。 图8 双向隐身KK平面介质[74]:(a)复介电常数ε(x)的谱,(b)和(c)分别是TE和TM极化波传输及反射系数谱Fig.8 Bi-directional stealth KK plane medium[74]: (a) is the spectrum of the complex permittivityε(x); (b) and (c) are TE and TM polarized wave propagation and reflection coefficient spectra, respectively 8.1.3 全频率无反射空间KK介质[75] 如果介电常数ε(x,ω)满足:在上半复平面解析,ε(x,-ω)=ε*(x,ω),虚部为正,ω→0时,ε(x,ω)~a(x)+b(x)ωn,n≥-1,ω→∞时,ε(x,ω)~1+c(x)/ω2,则介质在任何频率都没有反射,例如: (89) 其中,P(x,ω)=1+f(x)/(γ-iω)2,γ>0,f(x)=Ω2/2[1+tanh(-x/a)],a>0。 8.1.4 无反射及透射的空间KK介质[76] (90) (91) 8.1.5 空间-频率洛伦兹KK介质 图9 一维非均匀空间KK介质[77]。(a)印制卷绕金属丝制成的二维人工介质及几何参数;(b)具有91个单元的沿x方向的周期性条形结构;(c)利用全方位单极探针测量电场的实验系统;(d)测量及(e)仿真得到的2.4 GHz的电场分布;(f)y=0时,沿x方向的电场|Ez|的分布曲线Fig.9 1-dimensional non-uniform space KK medium[77]: (a)2-dimensional artificial medium made of printed rolled-up wire and its geometric parameters; (b)a periodic bar structure with 91 units along thexdirection; (c)an experimental system for measuring electric field by omnidirectional monopole probe; (d) and (e) are the electric field distributions of 2.4 GHz for measurement and simulation, respectively; (f)the distribution curve of electric field |Ez| along thexdirection asy=0 Dexin Ye等[77]提出了空间频率洛伦兹色散理论,如图9(a)和9(b)所示,通过将卷绕金属丝印制在电介质基底上制作了x方向周期性的空间KK人工色散介质,并在实验上观察到了2~3 GHz波段全方位无反射吸收,如图9(d)和9(e)。所设计的介电常数(92)式在空域和频域都满足KK关系。 (92) 其中,谐振频率ω0-qx与空间坐标x有关,q决定了其随x的改变率。 8.2.1 时域KK关系 单边带信号u(t)=ur(t)+iui(t)的时域KK关系为[78]: (93) (94) 8.2.2 单探测器、单偏振KK接收机[78-80] 入射到光探测器上的单边带信号可表示为E(t)exp(-iπBt)=E0+Es(t)exp(-iπBt),E0是连续本征光信号幅度,Es(t)是频谱在±B/2之间的复载波信号,当E0>Es(t)时是最小相位信号,其相位φE(t)能够从光电流强度I(t)=log|E0+Es(t)|2中唯一地提取出来,二者之间的KK关系为: (95) 由此可得: (96) 图10 (a)220 Gb/s单波长、单偏振、单探测器的基于KK关系的直接探测系统;(b)测量结果[80]Fig.10 (a)220 Gb/s direct detection system based on KK relationship with single wavelength, single polarization and single detector and (b)detection results[80] Xi Chen等人[80]实现了220-Gb/s的基于KK接收机的光通信系统(图10(a)),用KK关系计算光电流就能得到光场参数,单模光纤传输100 km无需色散管理,并降低了信号-信号拍频干扰(SSBI)5 dB,如图10(b)所示,但其只用到一个偏振态并且信号和载波之间的保护带太大。 8.2.3 偏振复用KK收发机[79-80] Xi Chen等人[80]搭建了基于图11(a)所示的偏振复用(PDM)收发机的4×240-Gb/s WDM PDM100 km的光通信系统,每一通道用KK算法独立地恢复出光场的两个偏振态分量,误码率BER明显降低(如图11(b)所示)。 图11 偏振复用KK收发机[79]:(a)原理图;(b)实验结果Fig.11 (a)Schematic diagram and (b)experimental results for polarization multiplexing KK transceiver[79] 8.2.4 斯托克斯向量KK收发机[81] (97) (98) 图12 斯托克斯向量KK收发机[80]Fig.12 Stokes vector KK transceiver[80] 法国数学家哈达玛有一句名言:在实数域中,连接两个真理的最短路径是通过复数域,著名的KK关系也许是对这句名言的最佳阐释。KK关系虽然是一个可以不依赖于任何实际模型而存在的纯数学关系,但其应用却涵盖了也许人类现在都无法想象的广大领域。 KK关系反映的是一个复变量看似具有不同涵义的实部和虚部之间的深刻联系,即实部在某点(频率、时间、空间等等,也可以是多个自变量,如N阶非线性KK关系的多角频率)的值由虚部所有点的值共同决定,反之亦然。比如介质的复折射率,其实部折射率表示光在介质中和在真空中传输速度之比,而虚部的消光系数则表示介质对光的吸收。入射光子在介质中会产生电子能级、振动能级和转动能级跃迁并消耗自身能量形成分子吸收光谱,同时使光速变慢。介质对某一频率单色光子的吸收以及使该光子的传输速度变慢,本质上是该频率的光子与所有频率处相应能级共同作用的结果,这正是KK关系对于介质复折射率所表达的物理涵义。 虽然KK关系的导出不需要借助任何物理模型,但它确实是物理实在的高度数学概括。KK关系本质上是希尔伯特变换的一个特例,而希尔伯特变换的最初定义是输入信号与物理上不可实现的冲击响应1/πt的卷积,因此广义的希尔伯特变换至少从现在来看仅仅是纯数学上的。 具有因果关系的平方可积函数,是希尔伯特变换到KK关系的一座桥梁。平方可积函数代表了一个连续的物理过程,而不具有因果关系的物理量是不存在的。因果关系从哲学上来说,就是有原因才会产生结果,结果不能发生在原因之前。对于光学响应函数而言,连接两个不同时空点的是光,因此信号传播速度不能超过光速的相对论条件成为了因果关系的一个推论。可以看出,因果关系在不同的物理实在中具有不同的表现形式,如果对于声信号,那因果关系就会变成信号到达之前不会产生声响应之类的语言,而对于量子纠缠系统,至少在现在看来联系两个好像具有超距作用的纠缠粒子之间的并非光子,因果关系的具体形式还不得而知。 由于因果性条件的保证,KK关系理论上可以应用到任何的物理实在中,比如已知的反射和透射响应函数、复介电常数、复折射率、复电导率、电阻抗、复磁导率、复原子散射因子、绝热压缩系数、声折射率、单边带时域信号、空间KK介质、各种非线性介质以及船舶动力学[82]等等,可以想象这只是KK关系应用领域的冰山一角,所以人们对它的研究至今仍如火如荼。KK关系的独特魅力除了它优美的数学形式和普遍的物理内涵外,它还带给了人们物理参数测量上的极大方便。比如为了得到响应函数的相位需要相对复杂的技术和系统,但根据KK关系只需要简单测量消光谱就可以方便地计算出来。 KK关系在应用中也有固有的不足,一般KK积分都是在0到∞之间,但实际能够测量的物理模型或已知的变量范围(比如光谱的带宽)总是有限的,这无疑会给计算结果带来截断误差,因而就有了各种积分范围的外推方法。一类方法是用一定的函数来逼近和代替积分范围之外的参数,比如常数、幂指数或多项式等;另一类方法是根据色散曲线的特点选择合适的积分限以使上下界的截断误差相互抵消;还有一种方法是用微分的形式,使得响应函数的消光谱在每个频点具有不同的权重,在吸收峰处最大,而在上下界以外可以忽略。另外,由于是特定频率的激发场引起了非线性吸收的改变,因此其频谱比线性吸收谱窄的多,在截断误差上具有天然的优势。 除了对积分限进行外推外,人们还发展了单减和多减KK关系,其核心思想是引入参数已知的所谓锚点,锚点使得KK积分的收敛速度加快,并有效地减小了截断误差,而且选取的锚点越多,理论上截断误差越小。另外,还发展了响应函数对频率微分的差分多减KK关系,相位对频率的微分正好是时间延迟,而时延的测量要比相位的测量方便的多。 总之,KK关系简单形式背后蕴藏无限可能,近百年来一直激励着人们不断地研究与探索,其应用领域的不断扩展,截断误差的精心修正,锚点方法的显著功效,大量实例的成功实施,好像它已经不再有新意了,但其最新进展使人们重新认识到,原来时域和空域也有KK关系,KK关系也可以通过构建空间色散介质来实现电磁隐身,也可以用来构建光通信的重要器件和系统以简单的结构实现更低误码率的信号传输。KK关系的这两个全新发展方向,在为人们提供全新思路的同时,也赋予了人们无比的信心,KK关系全新的概念和应用正等待着我们去探索和发现。5.3 响应函数

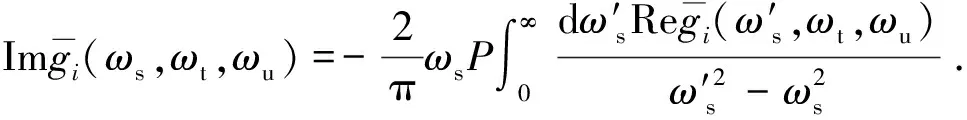
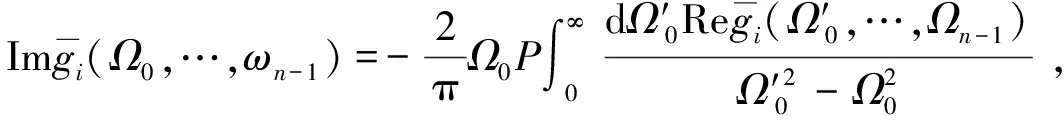
5.4 χ(2)晶体泵浦倒空导致的衰减与基波相移[56]
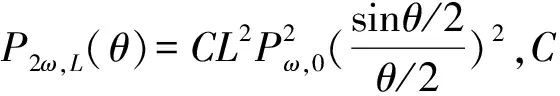
5.5 非线性复导电率


6 KK关系的截断误差及减小方法
6.1 截断误差


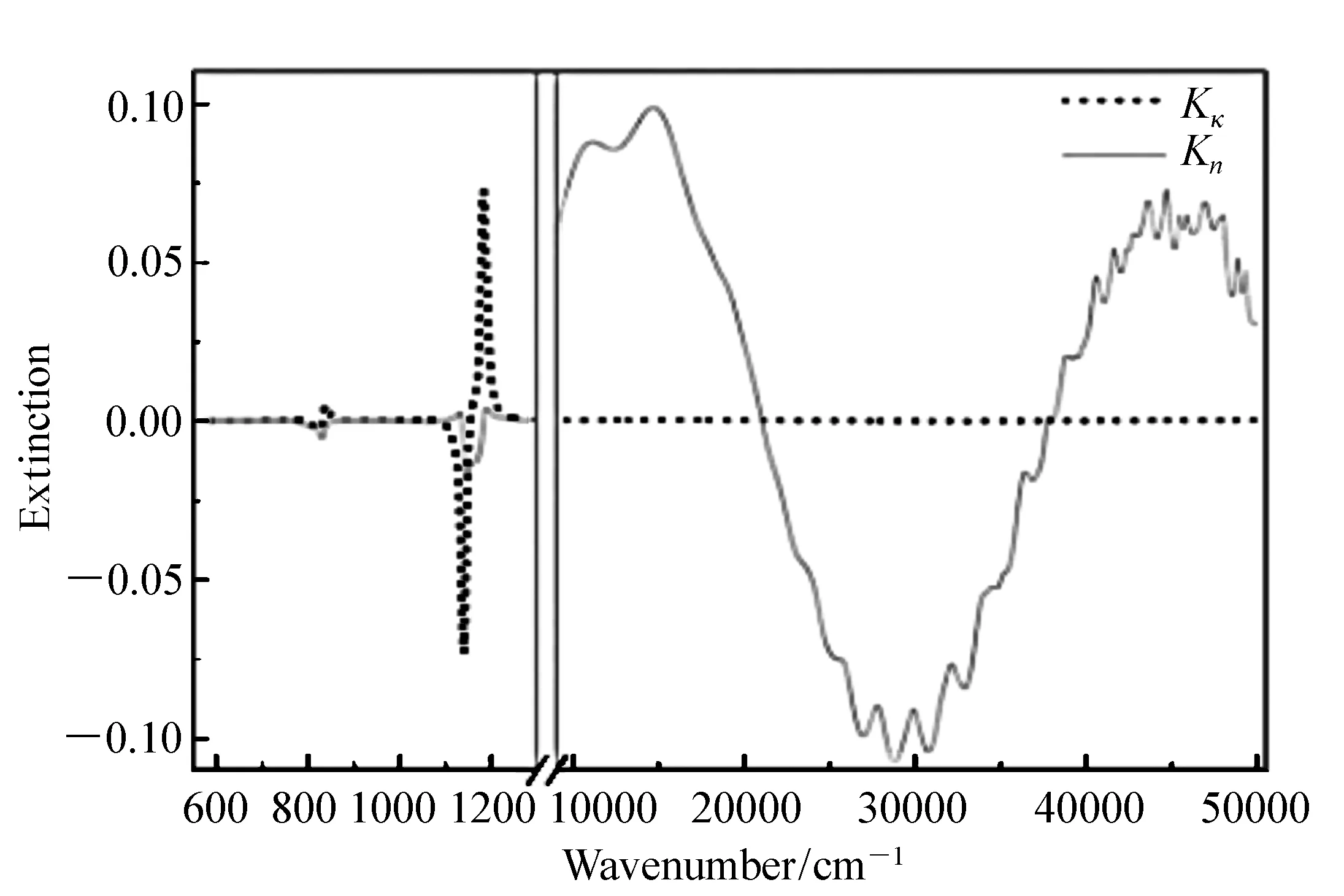
6.2 积分限的外推方法
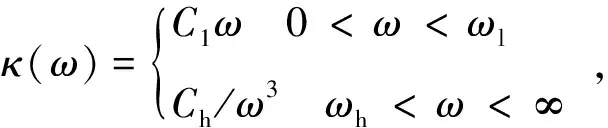
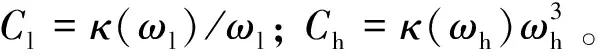

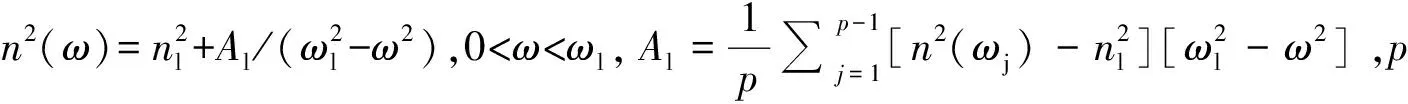
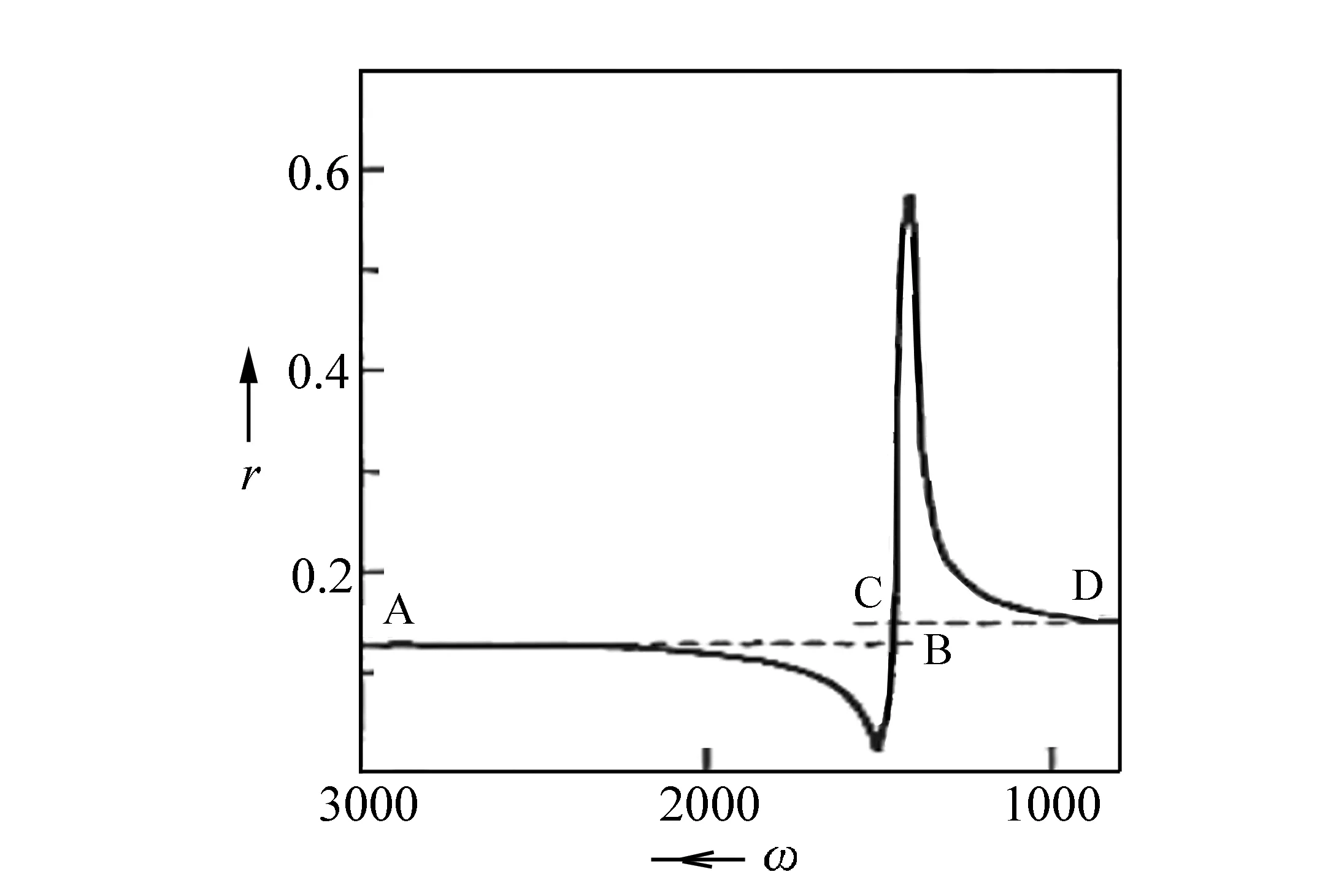
6.3 积分限选择法
6.4 微KK关系法
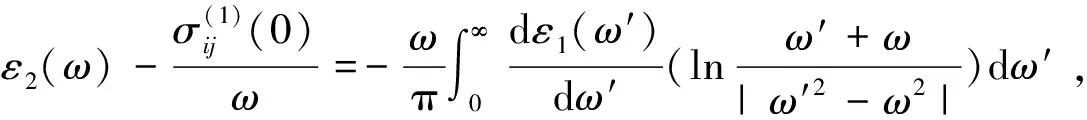
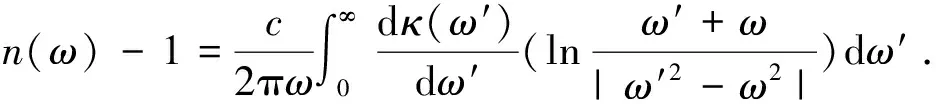
7 KK关系的修正
7.1 单减KK关系

7.2 多减KK关系
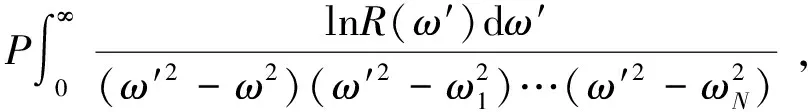
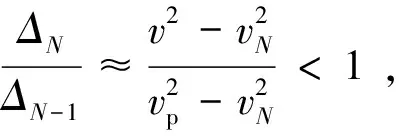


7.3 差分多减KK关系[69-70]
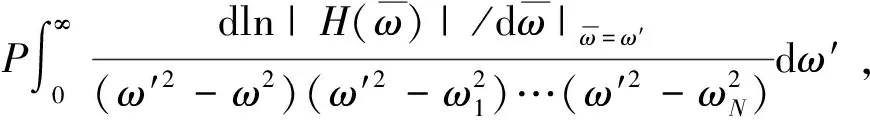

8 KK关系的新发展
8.1 空间KK关系

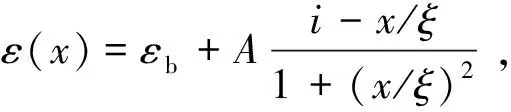
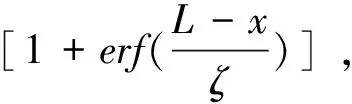





8.2 KK光通信器件
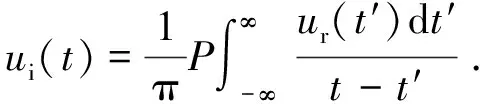


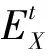
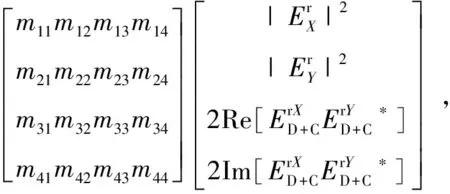



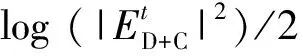
9 讨论及结论
