柱塞间隙厚度对柱塞泵水流动特性的影响分析
2019-05-13伟2平3
水 旭 锋,屈 波,樊 志 伟2,章 志 平3,朱 敏,章 勋
(1.河海大学 能源与电气学院,江苏 南京 211100; 2.济宁安泰矿山设备制造有限公司,山东 济宁272300;3.洪屏抽水蓄能有限公司,江西 宜春 330600)
1 研究背景
轴向柱塞泵通过柱塞在泵腔内做往复运动来压缩或扩张泵腔内的体积以达到压油与吸油的目的[1-2]。由于其结构紧凑、容积效率高、运行平稳以及可靠等优点而被广泛应用于液压设备中[3-4]。然而,作为评价柱塞泵的重要指标的容积效率,不仅受其自身结构和制造质量的影响,而且还受到一些其他条件的影响,比如温度、工作压力、油液黏度和柱塞间隙的厚度等[5]。目前,国内对柱塞泵有一定的研究,但还没有形成一个完整的体系,针对柱塞间隙厚度的大小与柱塞泵效率关系的研究相对较少[6-8]。
本文针对不同环形间隙厚度的柱塞泵进行CFD三维动网格数值模拟计算[9],并研究柱塞泵运行情况与环形间隙厚度对柱塞泵的影响、泄露量及其工作效率等问题,可为柱塞泵的日后投产使用提供一定的参考。
2 柱塞泵驱动分析及建模
2.1 柱塞泵模型建立
2.1.1柱塞泵结构
柱塞泵的二维剖面如图1所示。
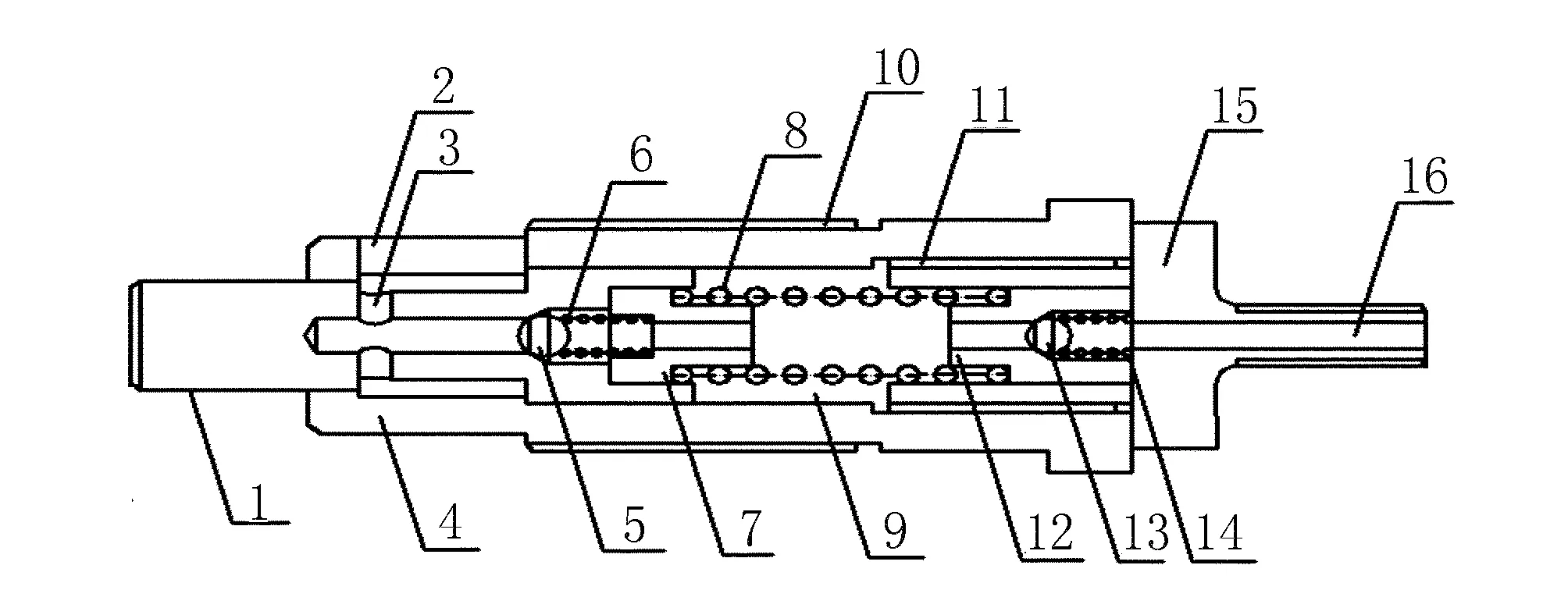
图1 柱塞泵二维剖面主视图Fig.1 Main view of two-dimensional section of plunger pump
由图1可以看出,柱塞泵的结构主要包括:1传动柱塞,2进油口,3进油管,4泵壳,5进油球形阀,6柱塞弹簧,7左侧环形凹槽,8油压弹簧,9泵体,10泵壳螺纹,11固定柱塞螺纹,12右侧环形凹槽,13出油球形阀,14柱塞弹簧,15固定柱塞,16出油口。
2.1.2柱塞泵三维模型
采用三维建模软件Pro/E建立了柱塞泵结构,模型如图2所示。

图2 柱塞泵三维模型Fig.2 3D model of plunger pump
2.2 柱塞泵传动柱塞运动特性分析
微型柱塞泵采用柱塞的驱动为椭圆凸轮,该驱动方式可以改变柱塞的运动规律,使柱塞泵的往复流量和压力基本无波动[10-11]。椭圆凸轮平顶从动件升程计算情况如图3所示。
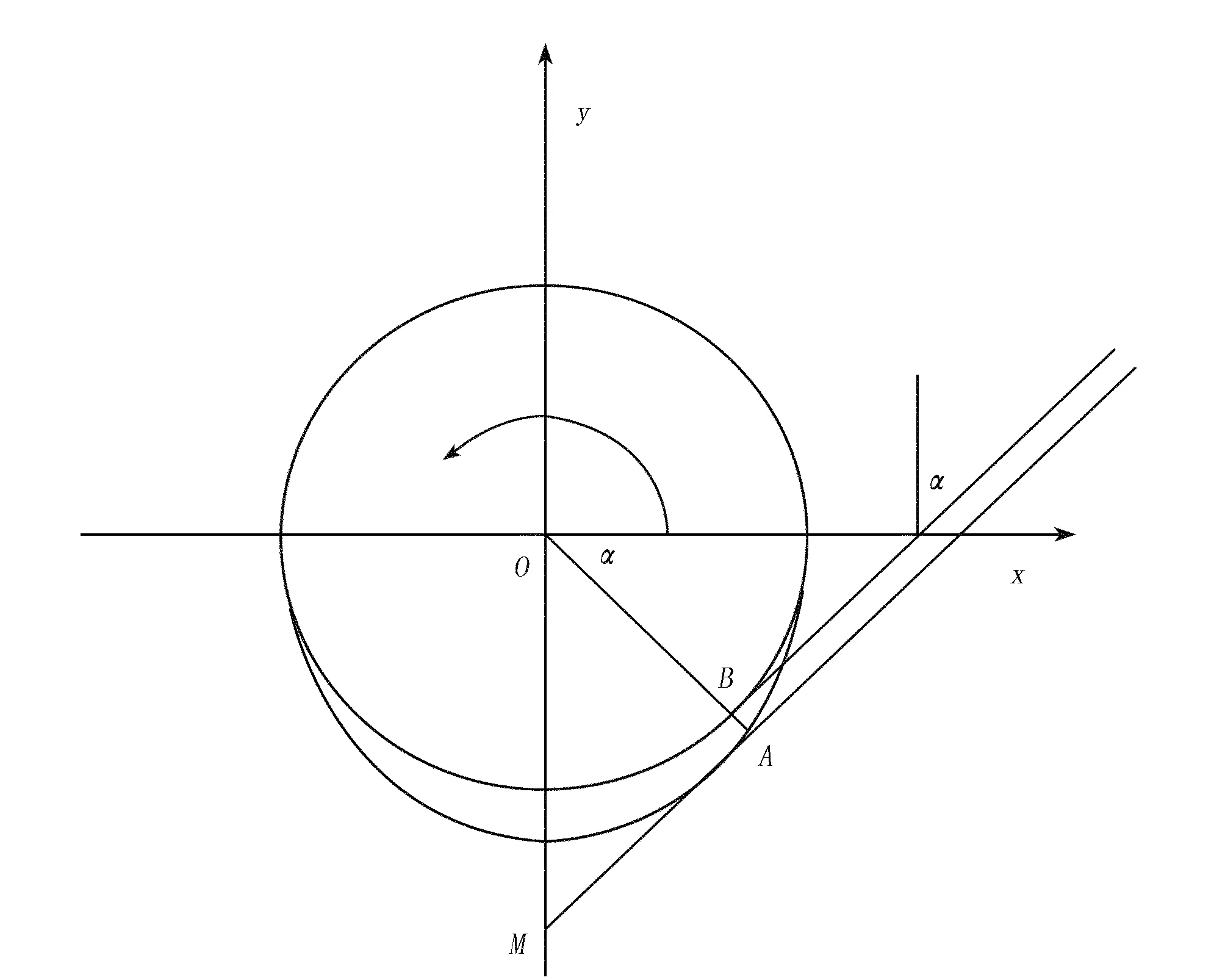
图3 椭圆凸轮平顶从动件升程计算Fig.3 Lift calculation of flat top follower of elliptical cam
利用反推法[12-13],得到的椭圆凸轮椭圆部分平顶从动件的升程为
h=asin2α+bcos2α-b
(1)
式中,a为椭圆凸轮长半轴,b为椭圆凸轮短半轴。椭圆凸轮转速n=120 r/min,则凸轮转动的周期T=0.5000 s,假定凸轮在0~0.2500 s属于椭圆轮廓时间区间,0.2500~0.5000 s属于圆轮廓时间区间。则椭圆凸轮平顶从动件升程h关于时间t的变化关系式如下:
(2)
椭圆凸轮升程h随时间的变化趋势如图4所示。在一个周期内,压油过程和吸油过程传动柱塞的位移曲线十分光滑、呈现为抛物线分布,而且两个过程的位移是对称的。在t=0.125 0 s时刻,即椭圆凸轮运动到椭圆轮廓的最高点,传动柱塞的位移达到最大,即0.02 m。在t=0.250 0 s时刻,椭圆凸轮运动到基圆轮廓,此时传动柱塞的位移为0,并一直保持到周期结束。
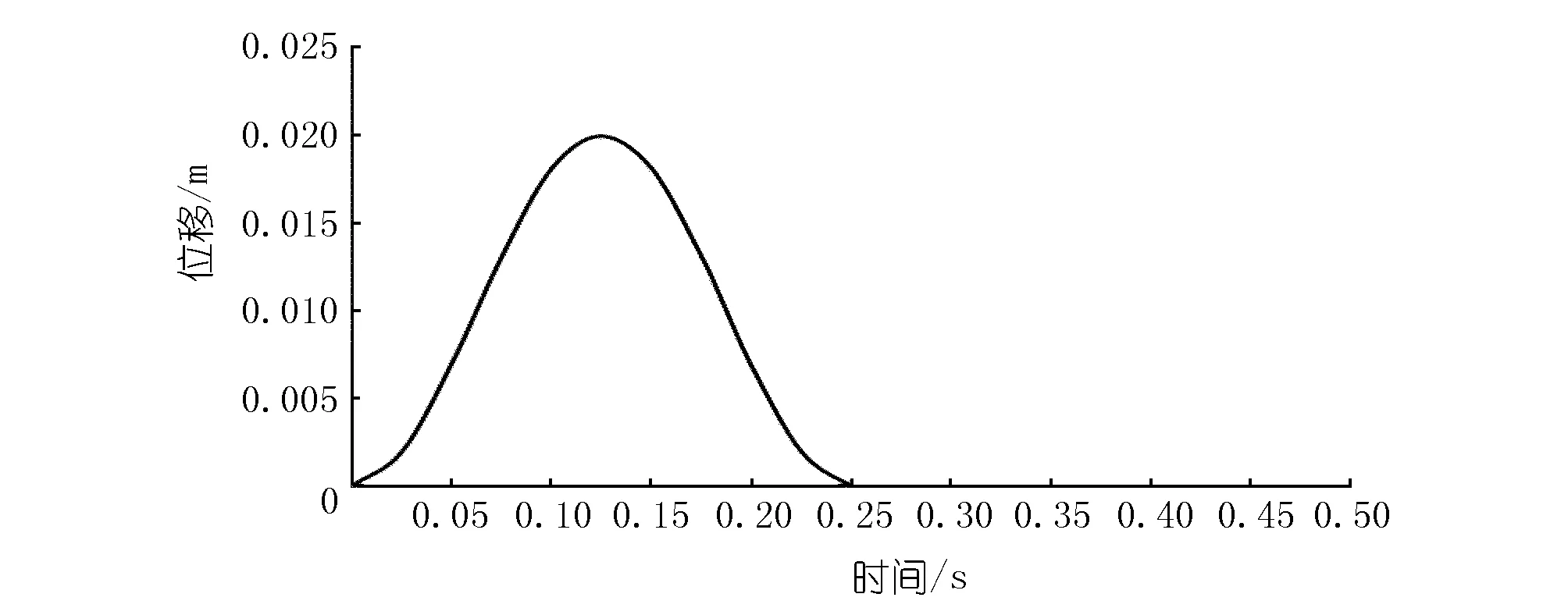
图4 柱塞泵传动柱塞位移Fig.4 Plunger displacement of plunger pump
通过对传动柱塞的升程h进行求导,可得传动柱塞的速度关于时间的变化趋势,如图5所示。在t=0.062 5 s时刻,传动柱塞速度达到最大值,约为0.25 m/s;在t=0.187 5 s时刻,传动柱塞的速度达到最小值,约为-0.25 m/s。
(3)

图5 柱塞泵传动柱塞速度Fig.5 Plunger speed of plunger pump
柱塞泵传动柱塞位移和速度的函数是任意阶可导的,说明在椭圆凸轮的驱动下,传动柱塞能够保持平稳的运动,压油和吸油期间没有速度的突变。在椭圆凸轮的设计中保留了半个周期的基圆轮廓。在基圆轮廓期间,柱塞泵传动柱塞保持静止,为柱塞泵内部流场以及进、出油球形单向阀提供充分的过渡时间,这样能够确保柱塞泵可持续稳定的工作,避免内部流场紊乱导致的柱塞泵的效率降低甚至是故障。
2.3 传动柱塞间隙分析设置
2.3.1柱塞泵环形油膜间隙
由于机械制造加工精度的原因,传动柱塞与泵壳之间存在间隙,如图6所示。在一般工程加工中,间隙大小为0.01~0.10 mm,间隙的存在会导致柱塞泵产生泄漏[14]。在柱塞泵工作过程中,间隙处也会形成环形油膜,环形油膜间隙可以降低传动柱塞与泵壳之间的摩擦力。可以说,柱塞泵的环形间隙是必不可少的。工作过程中环形间隙往往会产生一定的泄漏,一般由压差流和剪切流共同作用产生,通过计算泄漏量可以很直观地得出柱塞泵的工作效率[15]。
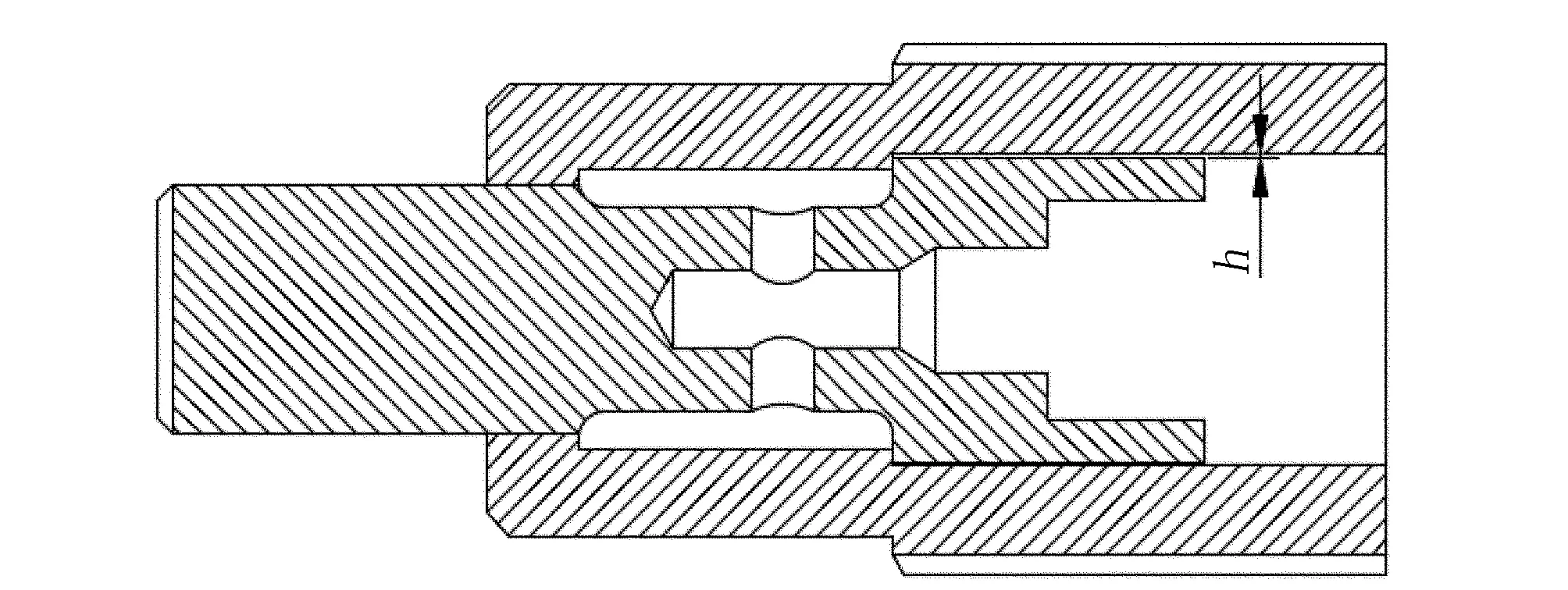
图6 柱塞泵环形间隙Fig.6 Annular clearance of plunger pump
2.3.2柱塞泵环形间隙设置
选取间隙大小为0.05 mm,建立带有环形间隙的柱塞泵模型、并采用gambit进行网格划分;采用四面体网格对环形间隙区域进行网格加密处理。由于环形间隙是随传动柱塞一起运动的,因此,在Fluent动网格设置中将环形间隙设为Rigid Body,其运动UDF与传动柱塞的运动UDF一致,其他设置与无间隙流动一致。
3 柱塞泵环形间隙流动特性分析
经过对柱塞泵的建模及运动设置后,导入 Fluent进行计算。针对不同的环形间隙所得到的计算结果进行了特性分析对比。
3.1 环形油膜间隙压力分布
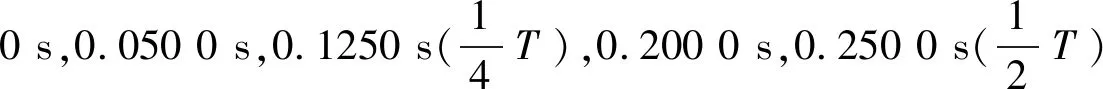

图7 柱塞泵环形油膜间隙压力分布(单位:Pa)Fig.7 Pressure distribution of annular oil film gap in plunger pump
由此可以做出以下推断:由于柱塞泵传动柱塞以及进、出油球形阀的运动只有轴向的平动,没有旋转运动,故柱塞泵的环形油膜间隙压力分布比较均匀,层次清晰。在压油过程,油膜压力为正压且沿正轴方向上压力逐渐减小;在吸油过程中,油膜压力为负压而且沿正轴方向的压力逐渐增大。
3.2 环形油膜间隙泄漏量分析
在传动柱塞停止运动时,可以认为其泄漏量为零。设定负轴方向为泄漏量为正的方向,则可将柱塞泵环形间隙的名义泄漏量分为两段分别进行计算[16-17]。
(1) 压油过程。
(4)
(2) 吸油过程。
(5)
上述两式中,d为环形间隙直径,m;h为环形间隙厚度,m;ΔP为环形间隙两端的压力差, Pa;μ为润滑油动力黏度Pa·s;l为环形间隙的轴向长度,m;u为传动柱塞运动速度,m/s。
若Q′(t)>0,则可认为产生泄漏,实际泄漏量Q(t)=Q′(t);若Q′(t)<0,则可以认为并未产生泄漏,实际泄漏量Q(t)=0。
通过将fluent计算结果进行汇总,可以得到各个时刻柱塞泵环形油膜间隙两端的压力差ΔP,传动柱塞的运动速度由式(3)给出。环形油膜间隙泄漏量的计算结果如图8所示。
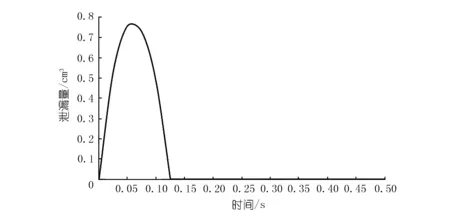
图8 柱塞泵泄漏量Fig.8 Leakage of plunger pump
由图8可以看出,柱塞泵的吸油过程(0.125 0~0.250 0 s)和停歇过程(0.250 0~0.500 0 s)没有产生泄漏。其中,吸油过程计算的名义泄漏量Q′(t)<0,说明Q′(t)的方向是沿正轴方向,显然这是不可能产生泄漏的。在压油过程(0~0.125 0 s)中,泄漏量随着时间的推进呈现为先增大后减小的趋势,呈抛物线的增长规律,可以认为压油过程产生的泄漏量与传动柱塞的速度为正相关,即传动柱塞负轴方向的速度越大,产生的泄漏量也越大。通过函数拟合逼近,可以得到泄漏曲线在0≤t<0.125 0 s时间段的表达式,即
Q(t)=-57 600.01t5+13 770.67t4-
672.81t3-237.33t2+27.34t
(6)
通过对式(6)进行求导,可以得到逼近函数在t=0.188 5 s处得到最大值。即在t=0.061 0 s时刻,泄漏量最大为0.770 cm3/s。
在柱塞泵完成一次压油、吸油的周期内,总的泄漏量为
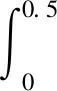
(7)
经计算,可以得到柱塞泵环形油膜间隙在一周期内的泄漏量为Q泄=0.066 cm3。
3.3 柱塞泵效率特性分析
3.3.1柱塞泵容积效率
柱塞泵一周期内的理论输油量为
Q理论=πR2D
(8)
式中,R为泵腔截面半径,cm;D为传动柱塞最大位移,cm。
在考虑环形间隙的条件下,柱塞泵一周期内的实际输油量为
Q实际=Q理论-Q泄漏
柱塞泵的容积效率为
(9)
通过计算,可以得到Q总=6.280 cm3,Q实际=6.210 cm3,柱塞泵的效率η1=98.9%。
3.3.2柱塞泵机械效率
柱塞泵的总的输入功率取决于传动柱塞泵的运动,柱塞泵是做正弦的往复运动。对式(3),即传动柱塞的速度进行求导,即可得到其加速度随时间的变化规律:
(10)
柱塞泵的输入功率:

(11)
式中,m为传动柱塞的质量,其材料选择35号钢,密度为7.85 g/cm3,体积为7.58 cm3。计算得到柱塞泵的输入功率P=7.52×10-3W。
柱塞泵内部的机械损失来源主要有以下3个方面:进油球形阀运动耗能、出油球形阀运动耗能与环形油膜间隙摩擦损失。
(1) 进油球形阀耗能。进油球形阀在压油过程中是随传动柱塞一起运动的,可以认为该过程的运动并不会引起能量的消耗。通过对进油球形阀位移特性的分析可知,其耗能的时间区间是在0.125 0~0.330 0 s。图9为柱塞泵的进油、出油球对形阀的位移情况。
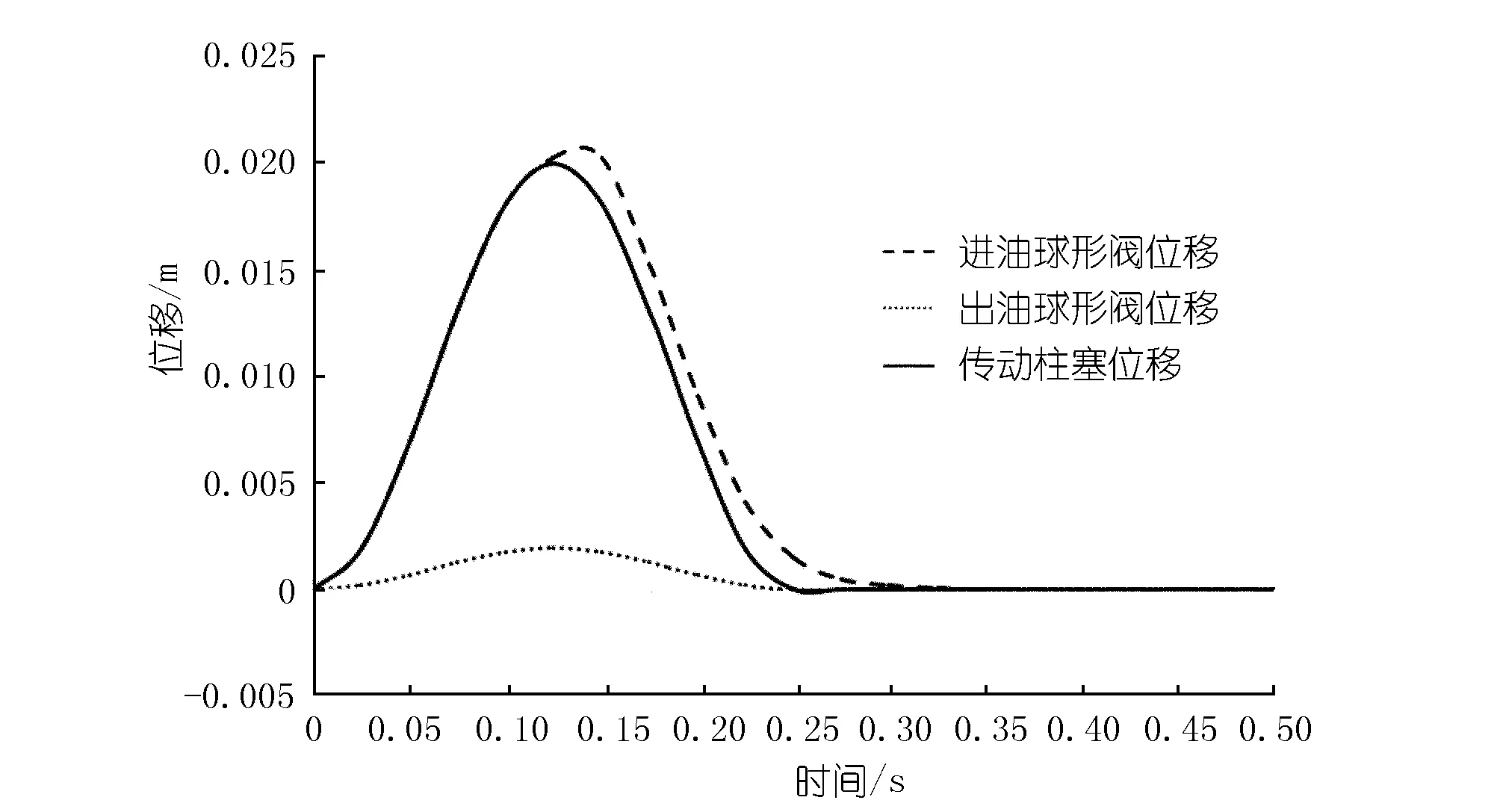
图9 柱塞泵进、出油球形阀位移Fig.9 The displacement of plunger pump inlet and outlet valve
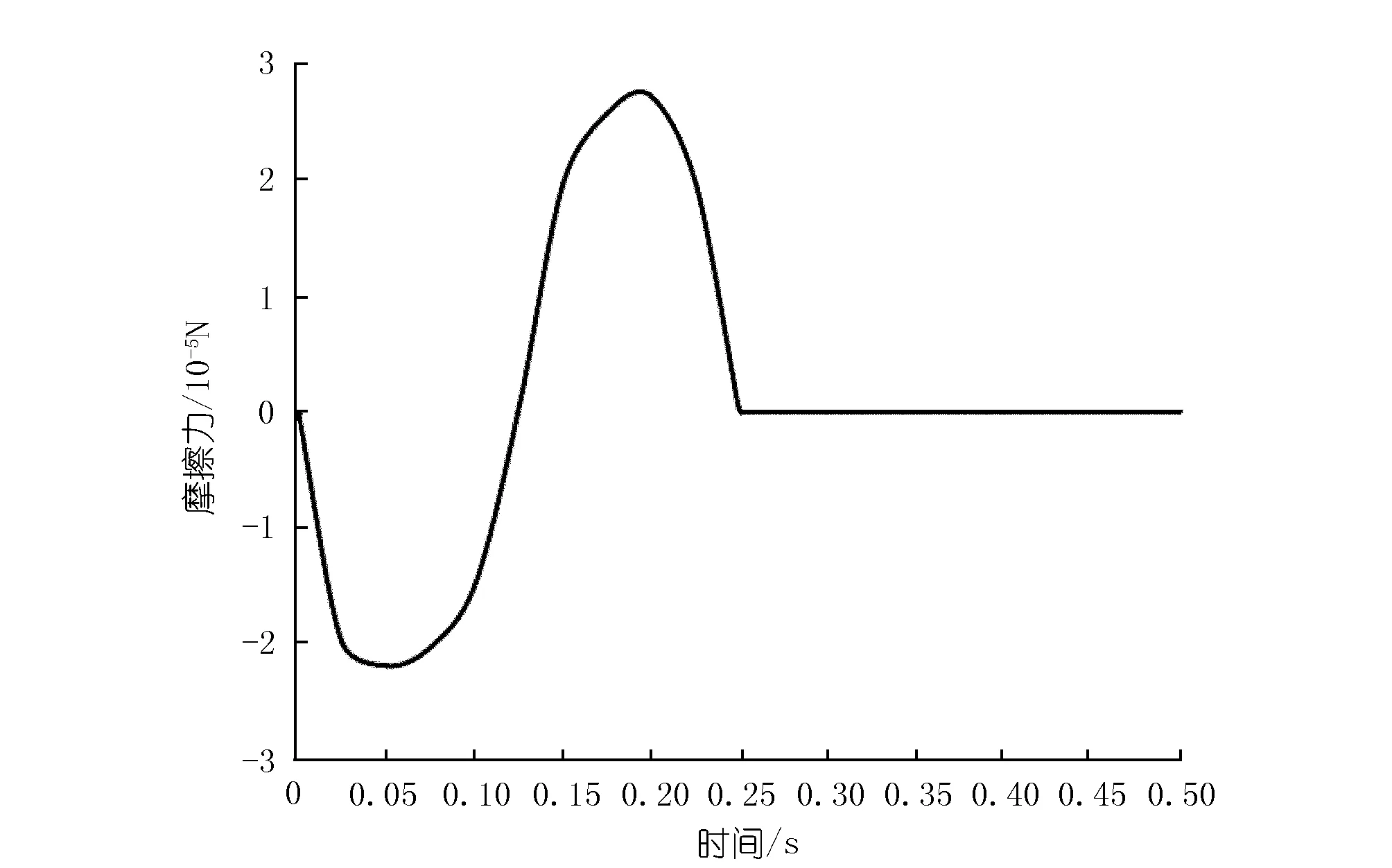
对进油球形阀位移曲线(见图9)进行插值拟合,可得到其在0.125 0s S1=2 667.37t6-3 226.79t5+1 452.13t4- 279.49t3+14.44t2+1.76t-0.14 (12) 进油球形阀运动耗能为 (13) 经积分计算,得到P1=2.13×10-4W。 (2) 出油球形阀耗能。通过对出油球形阀运动特性进行分析可知,出油球形阀是在压油过程及吸油过程中运动并且产生耗能的,对出油球形阀位移曲线(见图3和图4)进行插值拟合,可得其0 S2=-242.53t6+181.89t5- 41.47t4+1.79t3+0.25t2 (14) 出油球形阀运动耗能为 (15) 经积分计算,可得到P2=1.33×10-11W。相比较于输入功率和进油球形阀的运动耗能,出油球形阀运动耗能非常小,几乎可以忽略不计。 (3) 环形油膜间隙摩擦损失。根据流体液压力学,可得到环形油膜间隙处的摩擦力如下: (16) 式中各变量的说明与3式相同。 通过fluent计算结果报告,可得到各个时刻的柱塞泵环形油膜间隙两端的压力差Δp。环形油膜间隙摩擦力的计算结果如图10所示。由图10可以看出:环形油膜间隙处的摩擦力总是与传动柱塞速度方向相反。在压油过程中,摩擦力为负轴方向,且随着时间的变化先增大后减小;在吸油过程中,摩擦力方向为正轴方向,且随着时间的变化呈现为先增大后减小;同时还可知,吸油过程中的摩擦力比压油过程中的摩擦力稍大;在停歇过程中,摩擦力为零。 图10 环形油膜间隙摩擦力Fig.10 Friction of annular oil film gap 采用插值拟合的方法,可以得到0 F=10.060t6-6.936t5+1.723t4- 0.219t3+0.020t2-0.001t (17) 对式(17)求导可知,在t=0.055 0 s时,压油过程中的摩擦力达到负向的最大,为-2.21×10-5N;在t=0.188 s时,吸油过程中的摩擦力达到的最大为2.84×10-5N。 环形油膜间隙摩擦损失如下: (18) 经积分计算,可得到P3=1.21×10-4W。 综上所述,柱塞泵总的输出功率为 P输出=P输入-P1-P2-P3 (19) 柱塞泵的机械效率为 (20) 经计算可得,柱塞泵的输出功率P输出=7.19×10-3W。机械效率η2=95.6%。 柱塞泵总的效率η=η1·η2=94.5%。传统的柱塞泵效率一般在85%~95%之间。可见,该微型柱塞泵效率能够满足工程需求。 3.3.3环形间隙厚度对柱塞泵效率的影响 环形间隙是柱塞泵的一个重要指标,其厚度的大小能够直接影响到柱塞泵的运行效率。工程零件加工一般对误差间隙控制在0.01~0.10 mm之间。为了解环形间隙厚度对柱塞泵效率的影响情况,另设置有0.02,0.08 mm和0.12 mm的环形间隙厚度并对其进行数值模拟与效率计算[18-19]。其效率计算结果如图11所示。 图11 变环形间隙厚度下柱塞泵的效率Fig.11 Efficiency of piston pump under different thickness of annular gap 柱塞泵环形间隙厚度越大,柱塞泵的容积效率越低,且降低的速度逐渐增大。造成这种结果的原因为环形间隙厚度增大,柱塞泵的泄漏量加大,当间隙厚度增大到一定的程度,油膜黏滞作用的减弱会导致容积效率快速降低。同时,环形间隙厚度越大,柱塞泵的机械效率越高,但升高的速度会逐渐减慢。造成这种结果的原因为:当间隙厚度增大到一定的程度时,传动柱塞泵与泵壁的摩擦会减小到一个极限值,其主要机械损失来源于进油球形阀的运动耗能,将会导致机械效率升高的速度减慢。柱塞泵总效率是随着间隙厚度的增大呈先升高后降低的趋势,存在一个最优的间隙厚度值;从选取的间隙厚度值的计算结果来看,最优环形间隙厚度为0.05 mm,此时的柱塞泵的效率最高为95.6%。 本论文在研究过程中考虑了柱塞泵内环形间隙的影响,在变间隙厚度的情况下,对带有环形间隙的柱塞泵进行了数值模拟计算,得出的主要结论如下。 (1) 柱塞泵环形油膜间隙只在压油过程中会产生泄漏,在吸油过程和停歇过程中没有出现泄漏。在压油过程中产生的泄漏量随着传动柱塞负轴方向的速度增大而增大。 (2) 柱塞泵的容积效率随环形间隙厚度的增大而降低,但降低的速度逐渐减慢;机械效率随环形间隙厚度的增大而升高,但升高的速度逐渐减慢。 (3) 在间隙厚度为0.05 mm时,柱塞泵达到最高效率。
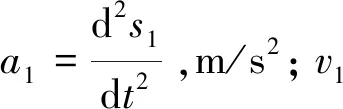

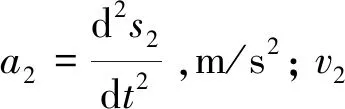
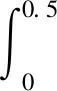

4 结 论
