基于随机介质理论的隧道开挖地表沉降规律研究
2019-05-13军王木宋方郭
苗 胜 军王 子 木宋 元 方郭 向 阳
(1.北京科技大学 土木工程系,北京 100083; 2.北京科技大学 城市地下空间工程北京市重点实验室,北京 100083)
地铁隧道开挖会对周围地层造成扰动,导致地表沉降,从而给周边建筑物和地下管线等设施带来安全隐患[1-2]。因此,准确预测隧道开挖引起的地表沉降具有重要的意义[3-4]。
隧道开挖引起地表沉降的预测方法很多,其中,Peck公式应用较为广泛,它是一种由高斯曲线拟合的用于预测隧道开挖地表横断面沉降槽分布的经验公式[5]。随后,Attewell和Woodman[6]基于Peck公式采用累积概率曲线描述了沿隧道开挖方向的地表沉降曲线。近年来,灰色理论法、神经网络法、数值模拟法、模型试验法等也被逐步应用于预测地表沉降。例如:胡斌等[7]利用灰色理论GM(1,1)模型对武汉地铁2号线广虎区间的隧道塌陷事故和地面沉降进行了分析预测。周志广和冀彦卓[8]以隧道开挖引起的地表沉降监测数据为基础,建立神经网络预测模型,对地面沉降的变化规律及其发展动态进行了预测。王建秀等[9]利用非线性有限元分析软件ABAQUS研究了隧道施工扰动下地表的横向和纵向沉降、地层的水平位移和分层沉降的变形规律。苑艺[10]采用物理模型试验研究了地铁隧道穿越地面沉降凹槽中心长轴和外侧边缘时地面沉降加剧对地铁隧道的影响机制。不同预测方法的适用范围不同,优缺点各异。Peck法适用于埋深大、半径小的隧道开挖,但采用Peck法预测的沉降槽分布随区域地质条件的差异变化很大。灰色理论法和神经网络法可以在监测数据少、变化趋势不明显的情况下进行地表沉降预测,但灰色理论或神经网络建立的“小样本”预测模型,在短期预测中具有较高精度,在长期预测中误差较大。数值模拟法具有能够考虑各种因素、描述材料非线性等优势,但计算结果的准确性依赖于本构关系和参数的选择,而且需要对很多状况进行近似处理,因此很难做到模拟结果与实际情况完全吻合。模型试验能更加准确地模拟隧道地表沉降的动态变化过程,结果直观明了,但模型试验难以完全满足相似条件,而且成本较高,因此未能得到广泛的应用。
此外,20世纪50年代,Litwiniszyn[11]为研究煤矿开采引起的岩层与地表移动问题提出了随机介质理论,基于统计学理论将整个巷道开挖对地表的影响等效于无限微小单元开挖对上部地层影响的总和。经过阳军生、韩煊等的研究,该理论被应用到露天与地下矿山开采及地层疏水所引起的地表移动预测领域[12-13]。20世纪90年代以来,随机介质理论开始被应用于预测不同地铁隧道开挖方法下地表的位移和变形。
浅埋地铁隧道开挖引起的地表变形同时受到隧道开挖断面尺寸、形状和收敛状况的影响,相比于Peck公式等预测方法,随机介质理论通过对隧道开挖前后断面面积进行积分来预测地层的沉降,能更好地反映隧道断面变化对地表沉降的影响[13]。本文结合哈尔滨地铁湘江路站-会展中心站区间(湘-会区间)大断面和标准断面并行隧道暗挖工程,以随机介质理论为基础,预测了不同断面尺寸、不同形状双线并行隧道施工引起的地表沉降规律,并采用实测数据和FLAC数值模拟对预测结果进行对比验证。
1 随机介质理论
1.1 任意单元开挖引起的地表沉降
隧道开挖对地层的影响可等效为许多无限微小单元开挖对地层影响的总和。对于地层采用整体坐标系(X,Y,Z),对于开挖部分采用局部坐标系(ε,η,ζ)。如图1所示,将宽度、长度、厚度均为无限小的开挖定义为单元开挖dεdηdζ,距离隧道掌子面较远处,隧道开挖可简化为平面应变问题(见图2)。假设距隧道中心X处的地表沉降为We(X)[14],由随机介质理论可知:
(1)
式中,β为开挖地层的主要影响角,η为单元体中心距地表的垂直距离,X为地表点距单元体中心的水平距离,ε为单元体中心距隧道中心的水平距离。

图1 单元开挖示意Fig.1 Sketch of element excavation
1.2 单线隧道开挖引起的地表沉降
假设隧道初始开挖断面为Ω,隧道建成后开挖断面由Ω收缩为ω(见图2),对单元开挖引起的地表沉降进行积分即可得到整个隧道开挖引起的地表沉降[15],即:
(2)

图2 隧道开挖断面变形收敛情况Fig.2 Section convergence after tunnel excavation
1.3 极坐标系下的隧道开挖地表沉降
式(2)为直角坐标系下的单线隧道开挖引起的地表沉降公式,适用于断面形状比较规则的隧道。而实际的隧道断面往往是不规则的,为了得到适用于任意断面形状的单线隧道开挖地表沉降公式,现将直角坐标系转换为局部极坐标系[16](见图3),即:
ε=X1+rcosθ
(3)
η=Z1-rsinθ
(4)
式中,X1为隧道外轮廓线局部某处圆弧段在整体坐标下对应圆心的横坐标;Z1为该圆弧段在整体坐标下对应圆心的纵坐标;r为该圆弧段半径。

图3 坐标系转换Fig.3 Coordinate system transformation
由二重积分换元公式可得:
(5)
如图4所示,对于隧道外轮廓线上任意一段圆弧,设圆心为(X1,Z1),半径为r2,起始角和终止角分别为θ1和θ2,假设该圆弧段发生均匀收敛变形,圆弧半径由r2收缩到r1,收敛值为Δr,由式(2)可得该段圆弧收敛引起的地表下沉值W(X)为
(X1+rcosθ)]2}rdrdθ
(6)
根据叠加性公理,则任意断面形状单线隧道开挖引起的地表沉降为

=W1(X)+W2(X)+…+Wn(X)
(7)

图4 任意圆弧段开挖示意Fig.4 Sketch of arc segment excavation
1.4 双线隧道开挖引起的地表沉降
若两条隧道相距较近,则并行隧道开挖的相互影响不可忽略。如图5所示,隧道1圆心坐标为(X1,Z1),初始开挖半径为R1,断面半径收敛值为Δr1。隧道2圆心坐标为(X2,Z2),初始开挖半径为R2,断面半径收敛值为Δr2。假设一条隧道施工产生的地表沉降为W1(X),另一条隧道施工产生的地表沉降为W2(X)。由式(7)可得:

W12(X)+…+W1n(X)
(8)

W22(X)+…+W2n(x)
(9)
根据叠加性公理,双线并行隧道施工所导致的地表沉降W(X)为
W(X)=W1(X)+W2(X)
(10)
2 工程算例
2.1 工程概况
哈尔滨地铁3号线湘-会区间自湘江路站起,由南向北沿红旗大街至会展中心站,采用浅埋暗挖法施工,该段地层由杂填土、褐色粉质黏土、褐黄色粉质黏土、中砂构成。如图6所示,左线隧道为宽6.20 m、高6.60 m的标准马蹄形隧道,采用台阶法施工;右线隧道断面为变截面马蹄形,最大断面开挖尺寸为宽14.15 m、高10.62 m、长10.00 m,与左线隧道净距6.20 m,采用双侧壁导坑法施工。标准断面隧道顶板埋深约12.50 m,底板埋深约19.10 m;大断面隧道顶板埋深约10.90 m,底板埋深约21.52 m。
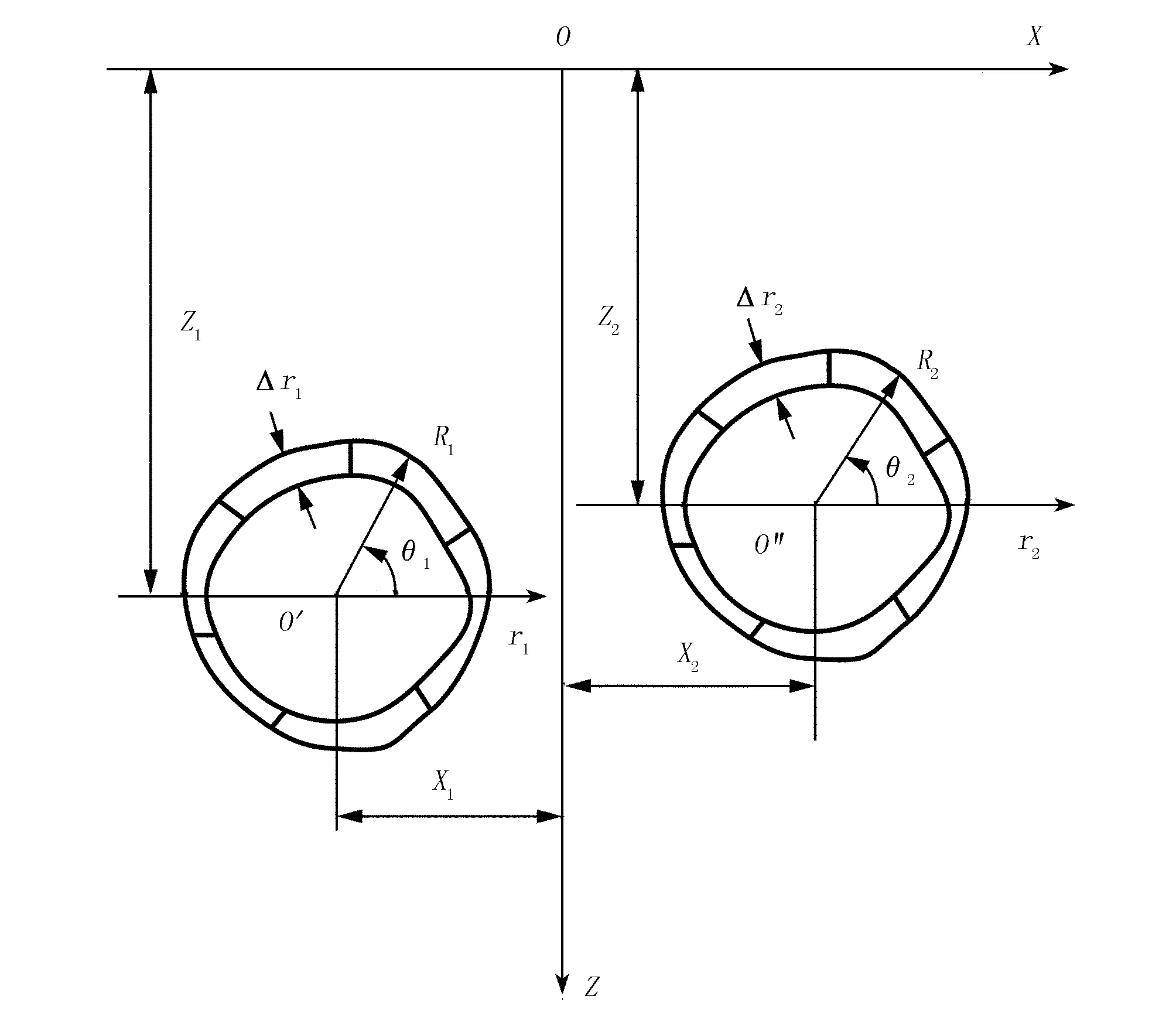
图5 双线并行隧道开挖示意Fig.5 Excavation of parallel tunnels

图6 隧道横断面位置关系(尺寸单位:m)Fig.6 Position relationship of the parallel tunnels
2.2 基于随机介质理论的地表沉降预测
2.2.1确定计算参数
由公式(1)~(7)可知,双线并行隧道施工引起的地表沉降与隧道间距L、埋深H、开挖半径R、断面半径收敛值Δr及tanβ有关。其中,tanβ=20/(50-φ),β为开挖地层的主要影响角,与隧道开挖所处的地层条件有关;φ为隧道开挖位置土层内摩擦角。根据表1,大断面开挖位置土层内摩擦角按各土层层厚所占总土层厚度比例取平均值可得:φ=18.406°,因此,tanβ=0.633;同理,求得标准断面内摩擦角φ为21.437°,tanβ=0.700。现场实测湘-会区间大断面隧道开挖断面半径收敛值Δr约为25.5 mm,标准断面隧道开挖Δr约为20.3 mm。

表1 土体参数Tab.1 Soil parameters
2.2.2计算流程与预测结果
施工现场在湘-会区间大断面变截面部位、车站与区间结合部位、车站与风道结合部位以及马头门处等部位设置了多个监测断面,每个断面布置7~11个测点,每个测点之间的距离为3~6m。如图6所示。以大断面与标准断面起始开挖位置的断面监测点作为实例进行预测。该监测断面共布置10个测点,以大断面与标准断面两条隧道中线处取X为0点,则各测点距离0点的距离分别为21.52,17.23,13.51,9.49,6.03,1.86,-2.77,-6.21,-10.46,-14.75 m。在此,以监测点D1-1为例,基于随机介质理论极坐标表达式预测该测点的地表沉降量,监测点D1-1的地表沉降量可视为大断面隧道6个圆弧段和标准断面隧道5个圆弧段开挖所引起沉降量的叠加之和。
(1) 大断面隧道开挖引起监测点D1-1地表沉降。大断面隧道平均埋深Z为16.21 m,两隧道中心平均间距L为16.375 m,X1为17.25 m,圆弧段1的开挖参数r1为7.075 m,tanβ为0.633,Δr为25.50 mm,r2=(r1-Δr),起始点与终止点弧度分别为0.681 rad、2.496 rad。应用MATLAB编制计算程序,计算得到圆弧段1开挖引起的监测点D1-1的地表沉降量W1=5.16 mm。同理,计算得到圆弧段2,3,4,5,6开挖引起的监测点D1-1的地表沉降依次为2.23,1.45,1.41,2.46,3.74 mm。则整个大断面开挖引起的监测点D1-1的地表沉降为16.45 mm。
(2) 标准断面隧道开挖引起监测点D1-1的地表沉降。标准断面隧道平均埋深Z为15.80 m,X2为-9.3 m,tanβ为0.700,标准断面圆弧段1的开挖参数r1为3.30 m,Δr为20.30 mm,r2=(r1-Δr),起始点与终止点弧度分别为0.471,1.571 rad。与大断面隧道开挖计算步骤一致,标准断面隧道各圆弧段开挖引起的地表沉降量为2.92+1.68+1.21+0.83+1.90=8.54 mm。
由叠加性公理,地表监测点D1-1的最终沉降量为24.99 mm。同理,可计算出该监测断面其他监测点的最终沉降量,结果见表2。

表2 监测断面的实测沉降值与预测沉降值Tab.2 Measured and predicted settlement of the section
2.3 基于数值模拟的地表沉降预测
采用FLAC3D建立大断面与标准断面隧道开挖数值计算模型。根据工程经验与圣维南原理,该模型沿隧道开挖方向取大断面实际开挖长度,近似为10 m;水平方向取133 m,竖直方向取52 m,上边缘取至地表。采用莫尔-库伦弹塑性模型进行数值分析,土体参数见表1。模型前后、左右边界及底面施加法向位移约束,上部取自由边界。隧道模型如图7所示,开挖后土体竖直方向位移见图8。

图7 隧道模型Fig.7 Tunnel model
2.4 对比分析
随机介质理论预测曲线与实测数据及数值模拟结果如图9所示。

图8 开挖后土体竖直位移云图Fig.8 Contour of Z-displacement after excavation

图9 预测结果与实测数据及数值模拟结果Fig.9 Predicted data, measured data and numerical simulation results
由表2和图9可知,沉降曲线并非沿两隧道中心线呈整体对称分布,而是偏向大断面一侧,随机介质理论预测的最大沉降距离隧道中心线6.03 m,最大值为45.36 mm;数值模拟的最大沉降距离隧道中心线7.49 m,最大值为47.45 mm。随机介质理论预测结果和数值模拟结果均比实测数据偏大。但随机介质理论预测曲线与实测地表沉降曲线拟合结果相对较好,最大沉降位置及变化趋势与实测曲线基本一致,且相对误差不超过25%。
3 结 论
(1) 基于随机介质理论,将直角坐标系转换为局部极坐标系,得出了任意隧道轮廓下的单线、双线隧道开挖引起的地表沉降公式。
(2) 以哈尔滨地铁3号线湘-会区间为例,基于随机介质理论极坐标表达式和FLAC3D数值模拟软件得到了大断面和标准断面并行隧道开挖引起的地表沉降及分布规律。
(3) 双线并行地铁隧道开挖的沉降曲线并非沿两隧道中心线呈整体对称分布,而是偏向较大断面尺寸隧道的一侧。
(4) 随机介质理论预测结果和数值模拟结果均比实测数据偏大。但随机介质理论预测曲线与实测曲线拟合较好,最大沉降位置及变化趋势与实测曲线基本一致,且相对误差不超过25%。
研究表明,基于随机介质理论的地表沉降计算结果同实测结果具有良好的一致性,该方法可以为地铁隧道施工影响预测提供依据。
