基于Fisher最优分割法的太湖调度线时段划分研究
2019-05-13
(太湖流域管理局 水利发展研究中心,上海 200434)
太湖调度线是太湖流域骨干工程调度的重要指示指标。现行的太湖调度线是通过实践经验总结得出的结果,反映了流域经济社会的发展、工程体系的健全和调控能力的变化。面对太湖流域经济社会发展的新形势、新要求,以及水雨情条件的新变化,从推进流域雨洪资源化利用,统筹兼顾防洪、水资源、水生态环境调度等角度,有必要开展太湖调度线时段划分的优化研究。
时段划分是太湖调度线的基础,时段划分的变化将引起太湖调度线相应发生改变。目前对于时段划分的方法较多,包括数理统计法[1-2]、变点分析[3]、Fisher最优分割法[4-7]、模糊集合分析法[8-10]、分形理论[11-13]等。王丽学等[14]在分析数理统计法、模糊集合分析法、层次聚类法的基本原理及各自优缺点的基础上,分别应用不同种方法研究了汤河水库汛期分期规律。刘克琳[15]等采用Fisher最优分割法,对海河流域密云水库进行了汛期分期研究。王中雅[16]等将分形理论应用到太湖流域洪水分期,计算了各分期的容量维数,确定了太湖全年分期数目。由于变点分析方法和分形理论均存在不同程度的主观性,而Fisher最优分割法数学概念清晰、更为客观、结果稳定,并且能够同时考虑多指标的综合作用和时序性[17-19],适用于时序性聚类。在分类数未知的情况下,Fisher最优分割法的计算较为繁琐,故本文在分类数已知的情况下,基于Fisher最优分割法的思路对太湖调度线时段划分进行优化研究。
1 Fisher 最优分割法原理及改进运用
1.1 Fisher 最优分割法原理
Fisher 最优分割法的分类依据是样本的总离差平方和最小,进行分割的原则是使得各类内部样本之间差异最小,而各类之间的差异最大[20]。
Fisher最优分割法计算步骤如下。
1.1.1数据处理
对于n个有序样本,每个样本均为m维向量,则可构建相关矩阵X:
若各指标之间的量纲不同,则需要通过下式进行无量纲化:
(1)
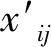
按照各指标对样本分类的重要程度,赋以不同的权重系数,加权平均后可将多指标特征值矩阵转化为一维特征值向量。
1.1.2定义类的直径
设某一类P包含的样本有{x(i),x(i+1),…,x(j)}(j>i),记为P={i,i+1,…,j}。该类的均值为
(2)
用D(i,j)表示这一类的直径,则可记为
(3)
1.1.3定义目标函数
最优分割的实质是找到某一组分点,使得各分类的总离差平方和最小,据此,定义目标函数为
(4)
目标函数值越小,表明分类内部差异越小,类之间差异越大。使目标函数值最小的那种分割就是最优分割,即
(5)
对于上式有如下定理:N个有序样本的最优k分割,一定是在其某一个截尾子段的最优k-1分割之后再添加一段形成的,因此B*(n,k)可由最优二分割的公式递推得出最优k分割的递推公式。假定分类数k已知,可由递推得到所有分类P1,P2,…,Pk,这就是最优k分类的分类结果。
根据分类结果,绘制目标函数随分类数k变化的曲线B*(n,k)~k,该曲线的拐弯处所对应的k值即为最优分类数。
1.2 Fisher 最优分割法改进运用思路
本文基于现状控制时段特性分析结果,在保障流域防洪安全的前提下,以现行的划分方案为基础方案,考虑对部分分点进行调整优化,以进一步增加太湖调蓄能力、减轻流域水资源供给压力,同时保障水生态环境安全。
在分类数未知的情况下,Fisher最优分割法的计算较为繁琐,首先需要假设所有可能的分类数,再通过递推得到相应分类P1,P2,…,Pk,最后确定最优分类数和对应的分类。由于本次是在现有的划分方案上进行优化研究,即分类数已知的情况下,因此以现有的方案为基础方案,对部分分点进行调整优化,设计计算方案集,计算各个方案的目标函数值,进而确定最优分类,能够极大地提高计算效率。
2 现行时段特性
2.1 流域概况
太湖流域位于长江三角洲的核心地区,城市众多、财富聚集、人口密集。流域内水系发达、河流纵横、水利工程众多、江河湖海相贯通,是典型的平原河网地区。太湖流域水面面积达5 551 km2,水面率为15%;河道总长约12万km,河道密度达3.3 km/km2。
2.2 现行时段及其特性
2.2.1现行控制时段
《太湖流域洪水与水量调度方案》根据太湖流域1954~2009年56 a梅雨资料和1949~2009年影响太湖流域的211场热带气旋(台风)资料分析结果,将全年划分为6个时段,见表1。
(1) T1:该时段为非汛期,流域降雨偏少;
(2) T2:该时段为汛前水位预降期(汛前期),用于提前预降太湖水位,为汛期降雨预留调蓄空间;
(3) T3:该时段为前汛期,主要考虑提高太湖的调蓄能力,力保太湖安全度汛;
(4) T4:该时段为梅汛期(主汛期);
(5) T5:该时段为台汛期,也是高温干旱期;
(6) T6:该时段为非汛期,降水总体较少。

表1 太湖调度线时段划分Tab.1 Division of Taihu dispatching line
2.2.2现行时段特征及合理性分析
根据1951~2013年太湖流域降雨资料,太湖流域多年平均降水量在年内呈 “双峰”型分布,第一个峰值处于6~7月,为梅雨期降水;第2个峰值处于8~9月,为台风雨期降水。时段雨强多年平均值显示,时段4和时段5多年平均雨强明显大于其余时段。其中,太湖流域降水量以时段4最为丰沛,多年平均时段雨强为6.45 mm/d,主要为梅雨期降水。时段5多年平均时段雨强为4.14 mm/d,仅次于时段4,降雨主要为台风雨。
根据1954~2013年太湖水位资料,1~3月太湖水位在全年内最低,自4月起随着流域降雨的增多,水位出现不同程度的上升,汛期太湖均处于较高水位,汛期结束后,水位较快回落。多年平均意义上,太湖水位以时段4和时段5最高,其次为时段6,其余时段多年平均水位相对较低(见图1)。太湖水位主要受到降雨和蒸发影响,同时也与水利工程调度有很大关系。一般而言,枯水期水利工程调度主要以保障供水安全为主;洪水期,遇流域性降雨,太湖和河湖水位齐涨,水利工程调度以保障防洪安全为主,并兼顾流域供水和水生态环境安全。例如时段5太湖防洪控制水位和调水限制水位高于时段4,一部分原因是考虑增加太湖蓄水量,缓解流域本地水资源不足。
陈墓、嘉兴为太湖流域阳澄淀泖区、杭嘉湖区地区代表站。陈墓站、嘉兴站长序列水位资料显示,夏季两站旬均水位保证率(本文中保证率定义为旬均水位满足允许最低旬均水位要求的年份在统计年份中的比例)较高,基本能够满足河道内生态需水的要求,但冬春季旬均水位多年保证率偏低,尤其是1~3月,说明河道内用水需求满足程度较低。
通过对太湖流域降雨、太湖水位和平原区代表站水位的时程规律分析,认为现行的太湖控制水位时段划分基本合理,但从平原区代表站水位、蓝藻防控,仍存在进一步的优化空间。
3 Fisher最优分割法在太湖调度线时段划分中的应用
3.1 时段划分方案设计
分点调整主要基于对流域降雨、太湖水位和地区代表站水位特性的分析。考虑到流域1~3月地区代表站旬均水位保证率偏低,拟将目前的时段1适当延长,即第1个分点后移5 d或10 d,增加太湖高水位控制时间。自上世纪90年代以来,太湖蓝藻暴发时间从6~9月延长到4~10月,且近几年部分年份全年均有蓝藻水华发生,考虑到太湖水位抬高对保障流域供水安全是有益的,拟适当提高时段2的太湖水位,即第2个分点后移5 d或10 d。此外,太湖流域人均水资源量不足全国平均水平的1/5,如何将洪水变成资源,是改善流域水资源短缺的一个重要的方向。《太湖流域洪水与水量调度方案》通过对太湖流域梅雨天气的长序列分析,得出流域多年平均出梅时间为7月8日,考虑到现行的时段4终止时间比流域多年平均出梅时间滞后十余天,拟将时段4缩短,即第4个分点前移5 d或10 d,同时有利于一部分雨洪资源的利用,由此构成时段设计方案见表2。
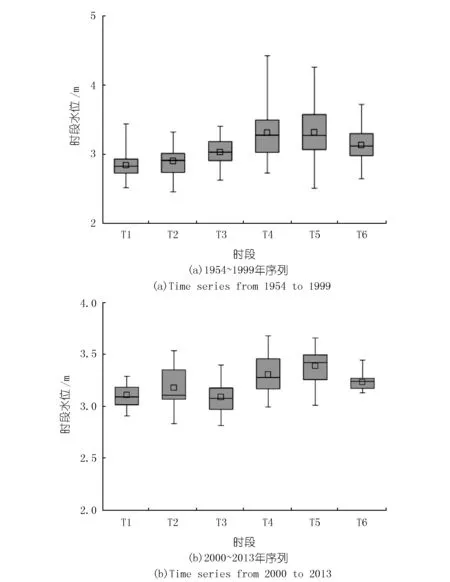
注:图中长线上端为最大值,下端为最小值,箱体中间线为中位数,箱体上端为上四分位数,下端为下四分位数,“□”为平均值。图1 太湖时段平均水位特征Fig.1 Mean water level in Taihu of each time interval

表2 太湖调度线时段划分设计方案Tab.2 Schemes of time interval division of Taihu Lake dispatching line
3.2 时段划分方案计算
3.2.1资料及指标选取
将全年期作为研究论域,以候为基本单位,进行降维处理,将整个论域划分为72个候。以1951~2013年太湖流域面雨量、1954~1999年太湖日均水位为基本资料,并选取最能反映太湖水位年内变化特征的5个因子为影响因子,即多年候内平均雨强、多年候最大1 d降雨量、候内降雨量超过25 mm的日数(d)、多年时段平均水位、多年候最高水位等。构建有序样本X,样本容量为72,每个样本均为5维向量。通过对太湖流域降雨、太湖水位年内特性的分析,研究时认为各个指标权重相等。
3.2.2数据处理
统计资料后得到样本的统计特征值,见表3,并进行标准化处理。

表3 样本统计特征值Tab.3 Characteristic value of index
3.2.3计算目标函数
利用公式(3)计算各类分段直径D(i,j),由于本次是在基础方案上的优化,因此仅计算时段设计方案集中涉及的各分类直径,见表4。进一步计算基础方案及设计方案目标函数值,结果见表5。
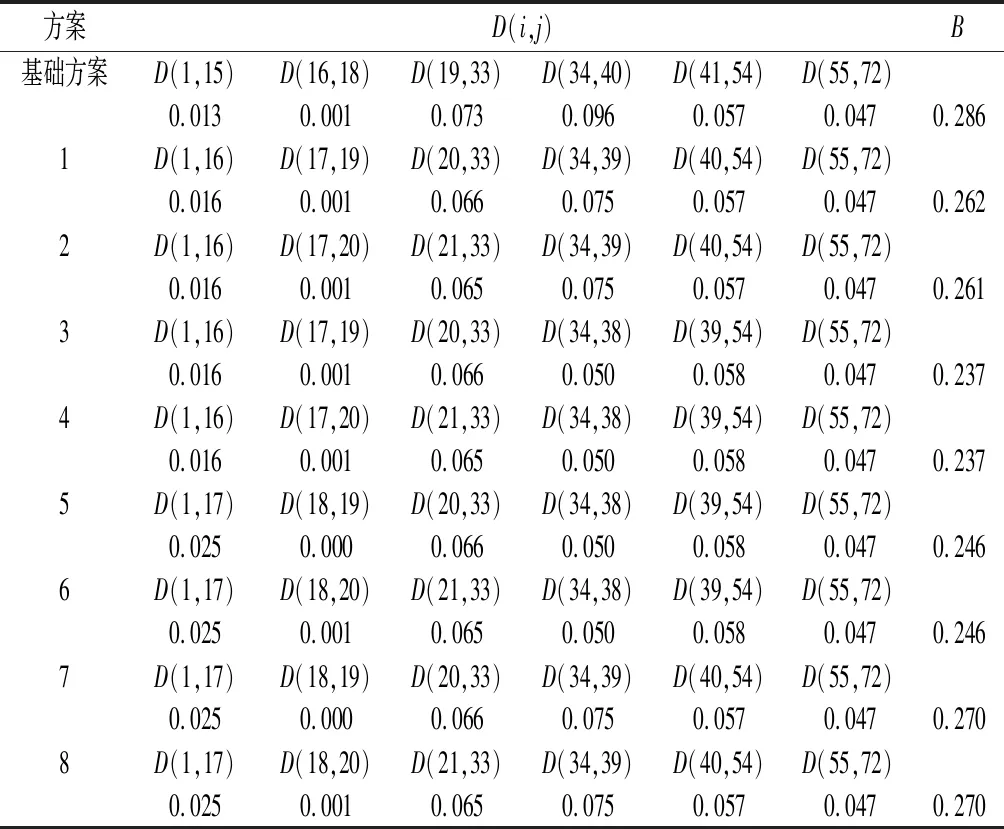
表5 各方案目标函数计算结果Tab.5 Calculated result of object function of each scheme
3.2.4最优分类
根据目标函数计算结果,方案3和方案4的目标函数值小于其他方案,因此方案3和方案4可作为最优的分割方案,即在现行的时段划分基础上,将第一个分点后移5 d,第二个分点后移5 d或10 d,第4个分点前移10 d。从水资源与生态环境的角度,本文认为方案4为最优分割方案。时段划分优化后,时段1延长了5 d,时段2延长了5 d,时段3缩短了10 d,时段4缩短了10 d,时段5延长了10 d,时段6保持不变,见表6。

表4 各类分段直径Tab.4 Diameter of all kinds of segment

表6 优化方案、现行方案划分时段对比Tab.6 Comparison of optimization scheme and current scheme
进一步分析时段调整后对流域防洪安全可能产生的影响。3月中旬多年平均降雨量较少,仅占全年降雨量的2.6%,基本无极值降雨发生,且太湖多年平均水位较低;4月上旬多年平均降雨量较少,仅占全年降雨量的2.8%,同样基本无极值降雨发生,太湖平均水位未超过3.50 m,因此,延长时段1,2不会对防洪造成影响,而有利于保障流域供水安全,满足流域河道内用水需求。7月中旬多年平均降雨量仅占汛期多年平均降雨量的6.9%,因此,将时段4结束时间提前至7月10日,不会对流域防洪安全产生较大影响。
4 结 论
本文基于太湖流域降雨和水位长序列资料,在现行时段划分方案的基础上,综合考虑了流域防洪、供水和水生态安全,对部分分点进行了调整,综合确定了太湖流域非汛期、汛前期、主汛期、汛后期。
(1) 本次将时段1结束时间推迟了5 d,时段2结束时间推迟了10 d,即延长了太湖高水位控制时间,有利于保障流域供水安全,提高地区代表站旬均水位保证率,满足流域河道内用水需求。同时,将时段4结束时间提前了10 d,有利于梅雨期结束后部分雨洪资源的利用。与现行方案相比,优化方案全面考虑了雨洪资源利用和太湖水生态环境安全,是更为综合的划分尝试。
(2) 在分类数已知的情况下,运用Fisher 最优分割法的原理,能够极大地提高计算效率,该方法具有一定的推广应用价值。
(3) 后续研究中可以考虑选取更多反映流域暴雨洪水特性、用水需求的指标,并根据各指标对分期的影响程度赋予不同的权重,以取得更为合理可靠的汛期分期结果。
