基于Copula函数的浙江沿海流域雨潮组合风险分析
2019-05-13
(浙江省水利水电勘测设计院,浙江 杭州 31002)
受地形特征和气候条件的影响,沿海地区的洪涝灾害受多种致灾因子共同作用,导致沿海地区的防洪排涝问题异常复杂。暴雨和潮位作为沿海地区两种典型的致灾因子,影响着该地区的防洪排涝,具体表现为当区域发生暴雨时,河口的潮位无法预知,当高潮位发生时,区域产生的降雨复杂多样,而传统的单变量频率分析不能准确反映暴雨和潮位对洪涝形成的相互作用关系,无法明确地给出洪潮遭遇的风险概率,无法解决复杂的防洪排涝问题。因此利用多维分析方法进行科学定量的沿海地区雨潮遭遇风险分析,为流域防洪排涝规划设计等提供设计参考十分必要。
目前,研究多变量联合分布的方法很多,而Copula函数因其不受边缘分布的限制,能够完整描述变量间的相关性,可根据实际情况灵活构造随机变量的多维联合分布,定量准确地计算出不同变量遭遇组合下的风险概率,且计算十分简便,因此在实际的水文事件组合分析计算中得到了广泛的应用[1]。Copula函数在水文水资源领域的应用主要包括干支流洪水遭遇分析[2-3],丰枯遭遇分析[4-5],洪潮及雨潮遭遇分析[6-7]等,但大部分的研究均集中于广东[8-9]、福建[10]和长江流域[2]等地区,对浙江省沿海地区的研究较少。
相较于传统的根据人为经验进行定性地雨潮组合判断的方法,本文采用多种不同的Copula函数构建了降雨与潮位的两变量联合分布,并最后选取最佳的Copula函数,对浙江省部分沿海地区的雨潮组合遭遇进行科学定量的风险概率计算和分析,为浙江省沿海地区的防洪排涝治理提供高效科学的决策参考。
1 雨潮二维联合分布构建
1.1 Copula函数的定义
根据Sklar定理[11]:令F是具有边缘分布函数为F1(x1),F2(x2),…,Fn(xn)的n维联合分布函数,若F1(x1),F2(x2),…,连续,则存在唯一一个Copula函数C,满足:
F(x1,x2,…,xn)=C[F1(x1),F2(x2),…,Fn(xn)]
(1)
式中,F1(x1),F2(x2),…,Fn(xn)分别为变量x1,x2,…,xn的边缘分布。
Copula函数的构建还有机结合了变量的相关程度,因此在推求多变量联合分布前还需计算变量的相关性。Kendall秩相关系数能够反映变量之间的线性和非线性相关关系,因此常用作变量间相关性度量指标[12],其计算公式如下:
yj)],i,j=1,2,…,N
(2)
sign[(xi-xj)(yi-yj)]
(3)
式中,N为数据长度;(xi,yi)为变量点数据。
1.2 二维联合分布推求
水文多变量联合分布常采用的Copula函数有AMH Copula,Frank Copula,Gumbel-Hougaard Copula,Clayton Copula,各方法特征及适用条件[6]见表1。

表1 不同Copula函数特征及适用条件Tab.1 The character and applicable conditions of different Copula functions
由于降雨和潮位具有非对称的尾部特征,因此,本文选取Gumbel-Hougaard Copula和Clayton Copula函数建立雨量和潮位的二维联合分布,其分布函数表达式如下。
GH Copula的分布函数表达式为
F(p,z)=C(u,v)=exp{-[(lnu)θ+(-lnv)θ]1/θ}
(4)
τ=1-1/θ,θ∈[1,∞)
(5)
Clayton Copula的分布函数表达式为
F(p,z)=C(u,v)=(u-θ+v-θ-1)-1/θ
(6)
τ=θ/(2+θ),θ∈(0,∞)
(7)
式中,F(p,z)为降雨量P和潮位Z的联合分布函数;u和v分别为降雨量P和潮位Z的边缘分布函数FP(p)和FZ(z);θ为Copula函数参数;τ为Kendall秩相关系数。
1.3 Copula函数优选
为了检验不同的Copula函数在多变量频率分析中的拟合精度,需要比较经验概率和理论概率是否一致。实测值(pi,zi)的经验累积概率计算公式[13]如下:
(8)
式中,N为联合实测值总个数;ni为实测值同时小于等于(pi,zi)出现的次数。
经验概率与理论概率的拟合程度采用OLS准则[12]进行拟合精度评价,OLS准则如下:
(9)
式中,Femp(pi,zi)和F(pi,zi)分别为经验累积概率值和理论累积概率值。OLS越小,说明Copula函数的拟合精度越高。
1.4 风险概率模型构建
为了定量分析不同的雨潮组合发生的概率,本文构建了3种不同的风险率模型,用于评价洪潮遭遇风险[14]。
(1) 同现风险率。同现风险率指降雨、潮位同时超过某一量级的概率。此情况是对城市防洪威胁最大、最不利的情况。其计算公式为
P风险(Z>z,P>p)=1-FZ(z)-FP(p)+F(p,z)
(10)
(2) 条件风险率。条件风险率是指已知发生某一量级的降雨时,发生超过某一量级的潮位的概率。其计算公式为
P条件(Z>z|P>p)=(1-Fz(z)-FP(p)+
F(p,z))/(1-FP(p))
(11)
(3) 防涝风险率。防涝风险率是指发生超过某一量级的降雨,或发生超过某一量级的潮位的概率。其计算公式为
P防涝(Z>z或P>p)=1-F(p,z)
(12)
其对应的防涝标准Tf计算公式为
Tf=1/(1-F(p,z))
(13)
对于任意设计标准的暴雨和潮位的组合,可通过其各自的边缘分布函数求得联合分布,从而得到各种风险率及防涝标准。同理,对于给定的风险率和防涝标准,也可求出不同暴雨重现期和潮位重现期的组合。
2 实例应用
2.1 温黄平原雨潮组合风险分析
温黄平原位于浙江省东部,椒江干流南岸、楠溪江以东、乐清湾以北,东部和东南部濒临东海,受暴雨及外海潮位共同作用,该地区洪涝灾害频发。本文选用温黄平原10个雨量站的年最大1 d降雨平均值作为本地区暴雨,暴雨发生后3 d内的海门站最高潮位[15]作为相应潮位,及海门站年最高潮位,分析“以暴雨为主,潮位相应”的温黄平原雨潮遭遇问题。
年最大1 d降雨、暴雨相应潮位及年最高潮位均采用P-Ⅲ型分布描述其边缘分布,经矩法和目估适线后,得到3个系列的边缘分布统计参数及设计值见表2。
分别采用GH Copula和Clayton Copula建立降雨和潮位的联合分布,各分布模型的统计参数值及理论频率与经验频率的拟合度见表3和图1。

表3 Copula函数的统计参数及拟合度计算成果Tab.3 The statistical parameter of Copula functions and calculation results of fitting degree
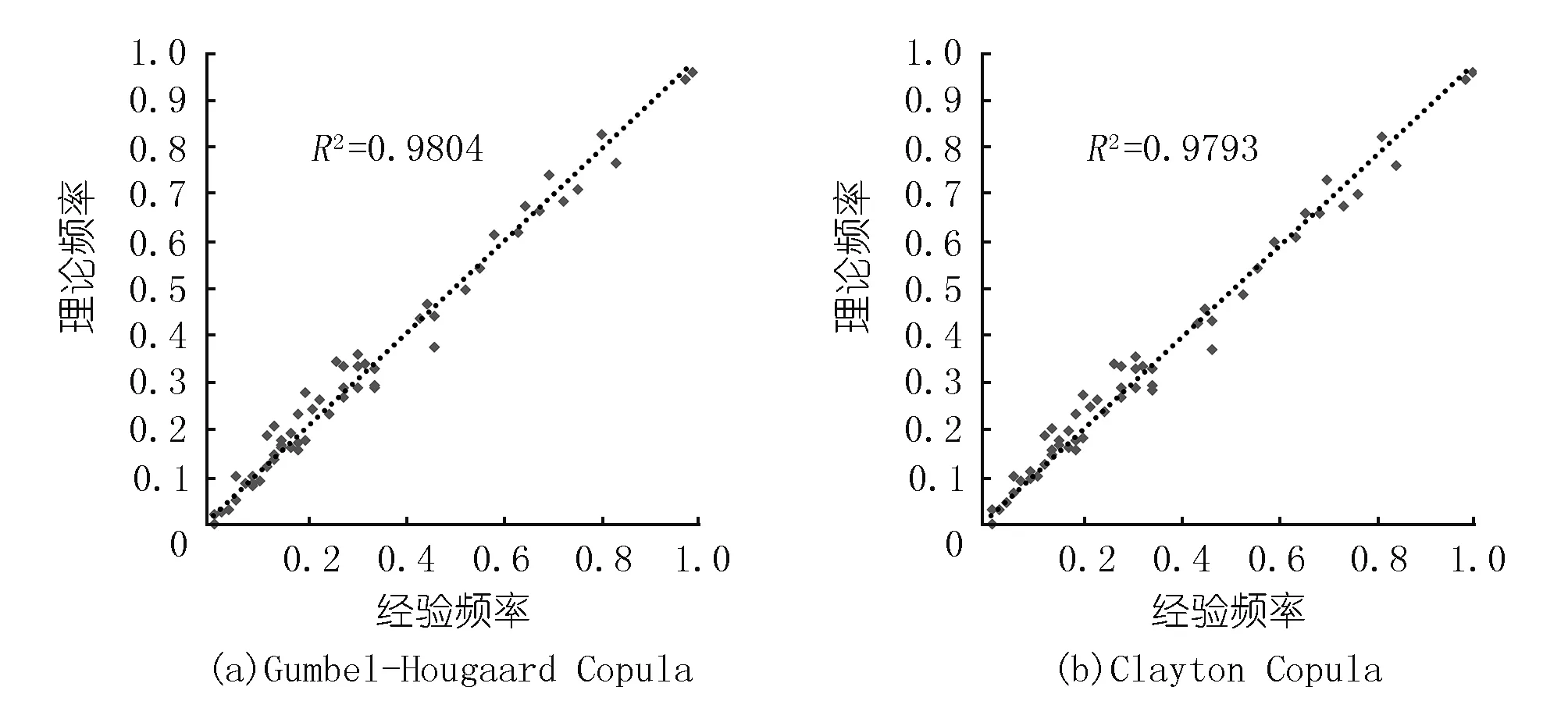
图1 不同Copula函数经验频率与理论频率拟合Fig.1 The fitness of theoretical joint distribution and experience joint distribution by different Copula functions
结果表明,Gumbel-Hougaard Copula的OLS较小,经验频率与理论频率的拟合度更好,说明其能更好地反映降雨和潮位之间的联合分布。因此,选取Gumbel-Hougaard Copula函数建立联合分布进行雨潮遭遇概率分析。
图2为以暴雨为主,潮位相应的雨潮同现风险率分布图。表4为根据构建的风险概率模型计算出的各种暴雨潮位组合下的风险率及防涝标准。
由表4和图2可以看出,随着潮位重现期的提高,遭遇同一重现期暴雨的概率逐渐减小,其防涝标准逐渐提高;不同重现期降雨遭遇20 a一遇以上潮位概率较小,最高不超过1.4%;且降雨和潮位组合下的联合风险率均小于组合中降雨的设计标准,即暴雨的重现期高于防涝标准。
在实际工程应用中,在选取暴雨和潮位的遭遇组合时,既需要考虑工程安全,达到一定的防涝标准,同时其遭遇也需要满足合理的条件概率。在实际的浙江省温黄平原防洪排涝规划设计中,采用传统的洪潮遭遇分析,确定50 a和20 a一遇暴雨遭遇20 a一遇潮位。当50 a和20 a一遇暴雨遭遇20 a一遇潮位时,对应的同现风险率分别为0.4%和0.7%,防涝标准为23 a和14 a一遇,条件风险率为22.5%和14.8%,既满足了较小的风险,达到了一定的防涝标准,同时也满足了较高的条件概率,说明设计较为合理。
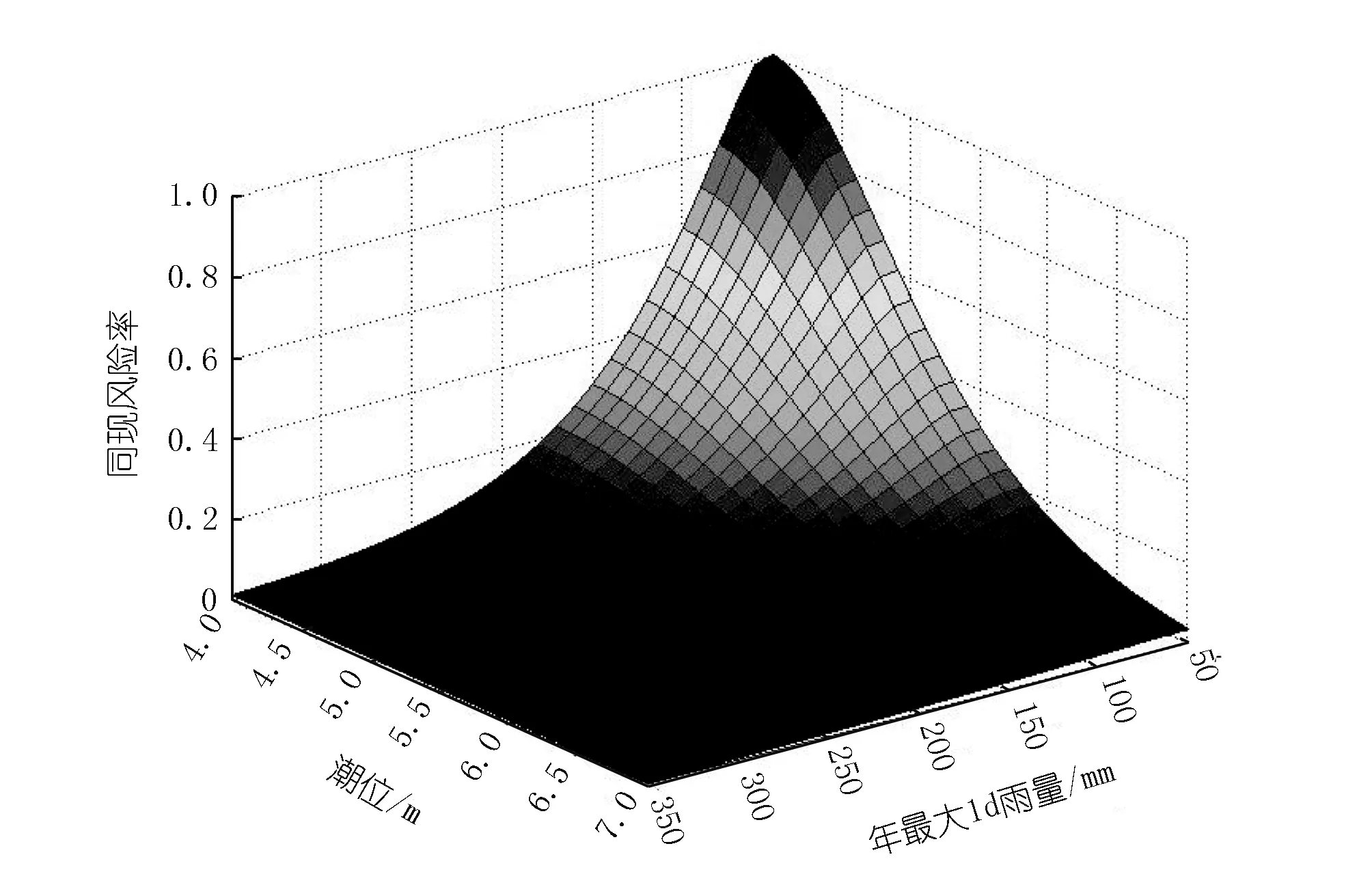
图2 以暴雨为主,潮位相应的雨潮同现风险率分布Fig.2 The distribution of simultaneous risk probability of rainfall and corresponding tide

表4 温黄平原不同暴雨潮位组合下风险率Tab.4 The risk probability of different combinations of rainfall and tide in Wenhuang plain
2.2 浙江省其他沿海流域雨潮组合风险分析
本文还将Gumbel-Hougaard Copula函数应用至鳌江流域、钱塘江流域等浙江省其他沿海地区进行雨潮组合风险分析,结果见表5。

表5 浙江省其它沿海地区不同暴雨潮位组合下风险率Tab.5 The risk probability of different combinations of rainfall and tide in other coastal areas of Zhejiang Province
从整体上看,在相同的暴雨和潮位遭遇组合下,鳌江流域和钱塘江流域的雨潮遭遇风险率较温黄平原更低,但其整体的变化规律与温黄平原的基本保持一致,且该成果与各流域防洪排涝规划设计中推荐采用的雨潮遭遇成果基本一致,进一步验证了Copula函数在雨潮遭遇应用分析中的适用性。
3 结 语
由Copula函数建立的雨潮联合分布精确定量地计算出了不同雨潮组合下的风险率,其在浙江省三大沿海流域的应用成果与流域防洪排涝规划设计中推荐的雨潮组合成果基本一致,说明了计算结果的合理性和可靠性。与传统的雨潮组合定性分析方法相比,该方法计算简便、灵活高效、实用性强,能够明确地给出不同雨潮组合下的风险概率,可为沿海地区工程设计提供决策参考。在实际工程应用中,建议同时结合条件风险率和防涝标准综合确定雨潮遭遇组合。
