A Distributed ADMM Approach for Collaborative Regression Learning in Edge Computing

Yangyang LiXue WangWeiwei Fang *Feng XueHao JinYi Zhang and Xianwei Li

Abstract:With the recent proliferation of Internet-of-Things(IoT),enormous amount of data are produced by wireless sensors and connected devices at the edge of network.Conventional cloud computing raises serious concerns on communication latency,bandwidth cost,and data privacy.To address these issues,edge computing has been introduced as a new paradigm that allows computation and analysis to be performed in close proximity with data sources.In this paper,we study how to conduct regression analysis when the training samples are kept private at source devices.Specifically,we consider the lasso regression model that has been widely adopted for prediction and forecasting based on information gathered from sensors.By adopting the Alternating Direction Method of Multipliers(ADMM),we decompose the original regression problem into a set of subproblems,each of which can be solved by an IoT device using its local data information.During the iterative solving process,the participating device only needs to provide some intermediate results to the edge server for lasso training.Extensive experiments based on two datasets are conducted to demonstrate the efficacy and efficiency of our proposed scheme.

Keywords:Internet-of-Things(IoT),edge computing,ADMM,lasso.

1 Introduction

In recent years,the fast penetration of Internet-of-Things(IoT)devices with various embedded sensors have significantly changed the way of information gathering,processing and sharing.Generally,it is impractical to run computation intensive applications at the IoT devices,since these devices are often constrained by on-board resources and battery capacity.This motivates development of IoT cloud platforms allowing offloading computation and analysis tasks to a resourceful centralized cloud[Truong and Dustdar(2015)].

Nevertheless,the cloud-based solution introduces unpredictably long latency for data communication through the wide area network,and incurs huge additional bandwidth occupation that may be beyond the capabilities of today’s Internet[Ha,Pillai,Lewis et al.(2013)].Furthermore,it would also bring about a number of privacy threats and security challenges[Zhou,Cao,Dong et al.(2017)].Therefore,it is more preferable to move computation and analysis to a close proximity of the IoT devices,i.e.,to the edge of the network.It is envisioned that edge computing would be a promising supplement to cloud computing[Shi,Cao,Zhang et al.(2016)],and make as much of an impact on human society as the latter.

By edge computing,it is feasible to conduct collaborative machine learning[Portelli and Anagnostopoulos(2017)]in real-time on site,obtaining useful information from data collected by a variety of IoT devices.For instance,the roadside base-station can use regression analysis to forecast short-term traffic flow by analyzing data originated from proximate GPS-enabled vehicles,video cameras and roadway sensors[Zhou,Cao,Dong et al.(2017);Shi,Cao,Zhang et al.(2016);Xi,Sheng,Sun et al.(2018)].Another good example is equipment maintenance,which uses multi-sensor information(e.g.,temperature,sound and vibration)to construct classifiers for fault detection and diagnosis[Kwon,Hodkiewicz,Fan et al.(2016)].In such systems,edge analytics is usually performed in a centralized fashion,i.e.,each involved device sends its own data samples to a dedicated edge server for training and building learning models.However,this centralized solution suffers from three drawbacks.Firstly,many machine learning algorithms require to solve a particular convex optimization problem.According to previous studies[Dhar,Yi,Ramakrishnan et al.(2015);Boyd,Parikh,Chu et al.(2011)],the traditional centralized solver does not scale well with increasing volume of data.Secondly,not all edge servers are as resourceful as cloud servers to run sophisticated tools for single-node in-memory analytics[Dhar,Yi,Ramakrishnan et al.(2015);Ismail,Goortani,Karim et al.(2015)].Thirdly,IoT-generated data may contain private and sensitive information(e.g.,healthy state of wearable users)that should not be directly exposed to the edge server or other devices[Zhou,Cao,Dong et al.(2017);Gong,Fang and Guo(2016)].To tackle these challenges,it is desirable that the learning solution for edge computing can jointly take scalability,performance and privacy issues into consideration.

In this paper,we are particularly interested in lasso(i.e.,least absolute shrinkage and selection operator[Tibshirani(1996)]),a classic linear regression technique that combines regularization and variable selection together for prediction and forecasting.This technique has already been used in a lot of IoT applications,e.g.,battery availability prediction for IoT devices[Longo,Mateos and Zunino(2018)],and internal temperature forecast for smart buildings[Spencer,Alfandi and Al-Obeidat(2018)].Specifically,we develop a distributed,collaborative learning solution that utilizes sampling data from multiple IoT devices for training lasso regression models.Based on the Alternating Direction Method of Multiplies(ADMM)[Boyd,Parikh,Chu et al.(2011)],the proposed scheme naturally decomposes the target optimization problem of lasso into small sub-problems that can be solved by each participating device using its local data.Unlike centralized solutions[Lon-go,Mateos and Zunino(2018);Spencer,Alfandi and Al-Obeidat(2018)],in our scheme the edge server only needs to collect locally trained intermediate parameters from IoT devices,and performs a simple aggregate operation to obtain the objective lasso model.The edge server and IoT devices work in such a collaborative way for multiple iterations until the lasso model converges.We have conducted extensive experiments based on two datasets with various system configurations.The experimental results show that our scheme quickly converges to near-optimal performance in a few tens of iterations.As compared to other benchmark solutions,it performs well in terms of efficiency and scalability,while obtaining a resulting lasso model with modest accuracy.

The rest of this paper is organized as follows.A brief review of existing work is presented in Section 2.Section 3 describes the system model and derives the problem formulation.In Section 4,we elaborate and discuss the proposed ADMM-based algorithm.Section 5 illustrates and discusses simulation results.Finally,we conclude this paper in Section 6.

2 Related work

Traditional machine learning algorithms [Tibshirani (1996); Spencer,Alfandi and Al-Obeidat(2018)]and tools[Boyd,Parikh,Chu et al.(2011)]are implemented using a fully centralized architecture,which requires a dedicated server with powerful computation capability and huge amount of memory.However,they fail to scale well with increasing size of data in the big data era.To address this challenge,various approaches have leveraged distributed data-parallel platforms to develop distributed machine learning libraries,such as Apache Mahout and Spark MLlib[Dhar,Yi,Ramakrishnan et al.(2015)].These platforms and libraries can significantly speed up the large-scale data analytics by coordinating the operations of multiple servers[Richter,Khoshgoftaar,Landset et al.(2015)].Nevertheless,they are not suitable to be applied for model learning in edge computing,due to resource constraints[Shi,Cao,Zhang et al.(2016)]and privacy concerns[Zhou,Cao,Dong et al.(2017)].

Considering that convex optimization is at the core of most machine learning algorithms,recent years have seen a number of distributed learning algorithms based on iterative methods[Dhar,Yi,Ramakrishnan et al.(2015)],which use successive approximations to come closer to the optimal solutions in each iteration.Among them,Stochastic Gradient Descent(SGD)is the most influential technique for solving linear prediction problems,e.g.,logistic regression.Zinkevich et al.[Zinkevich,Weimer,Smola et al.(2010)]propose the first parallel SGD algorithm that brings very little overhead on both I/O and communication.Meeds et al.[Meeds,Hendriks,Al Faraby et al.(2015)]develop a SGD-based javascript library that enables ubiquitous compute devices to run training algorithms in web browsing environments.With similar motivation to ours,McMahan et al.[McMahan,Moore,Ramage et al.(2017)]study the SGD-based distributed model training by iteratively aggregating locally trained parameters from edge devices.Although very efficient and easy to implement,SGD algorithms generally have a slow convergence rate due to their stochastic nature[Dhar,Yi,Ramakrishnan et al.(2015)].How to accelerate the convergence of SGD still remains as a challenging issue[Allen-Zhu(2017)].Recent research progresses on ADMM[Boyd,Parikh,Chu et al.(2011)]make it a competitive technique for solving distributed optimization and statistical learning problems.ADMM integrates the fast convergence characteristics of the multipliers method with the decomposability of the dual ascent approach,and can quickly converge to modest accuracy.This technique can be used to solve many supervised learning algorithms on regression and classification[Dhar,Yi,Ramakrishnan et al.(2015)].For example,Zhang et al.[Zhang,Lee and Shin(2012)]propose a distributed linear classification algorithm to solve the support vector machine problem.Gong et al.[Gong,Fang and Guo(2016)]design a privacypreserving scheme for training a logistic regression model based on distributed data from multiple users.However,the private aggregation mechanism used in Gong et al.[Gong,Fang and Guo(2016)]are proved to be inefficient and not suitable for resource-constrained devices[Joye and Libert(2013)].The work most relevant to ours is Bazerque et al.[Bazerque,Mateos and Giannakis(2010)],in which a consensus-based distributed algorithm is developed for in-network lasso regression.This algorithm is designed for networked systems with no central coordination,e.g.,wireless sensor network.A device needs to communicate with its one-hop neighbors frequently for updating intermediate parameters,resulting in heavy communication overhead and low convergence rate in large networks.

3 System model and problem formulation

3.1 System model

We consider edge systems consisting of an edge server,andNhomogeneous IoT devices performing a common sensing task.The IoT device continuously generates sensory data,and transforms the raw data in a certain time duration into a feature vector.Each feature vector consists of more than one predictor variables,and corresponds to an response variable.The edge server is responsible for performing data analysis and modelling the relationship between feature vectors and response variables.The resulting model is learned and built in a collaborative fashion at the edge server based on data samples from all participating devices.

The prediction model considered in this work is a lasso regression model [Tibshirani (1996)],which is a classic linear regression technique widely used for prediction and forecasting.Here we briefly introduce its basics.Given input training data set{(xi,yi),i=1,...,N},wherexi∈Rndenotes a feature vector andyi∈R denotes the corresponding response variable,the lasso model solves the following optimization problem:

wherew∈Rnis the weight vector,b∈R is the intercept,andλ＞0is the regularization parameter.With the trained lasso model(w,b)and a given feature vectorx∈Rn,we can estimate the value of response variableas follows:

Although very effective in practice,current lasso implementations[Longo,Mateos and Zunino(2018);Kwon,Hodkiewicz,Fan et al.(2016)]generally require that the participating devices contribute their native data to the edge server for model training.This would cause privacy leakage problems[Zhou,Cao,Dong et al.(2017)],as the native data could reveal private or sensitive information about device users. We assume that standard network security mechanisms[Zhou,Cao,Dong et al.(2017)],such as encryption and authentication,are applied to protect data storage and network communication of IoT devices from outsider attacks.Nevertheless,the edge server may not be trustworthy,and can still be a potential source of information leakage.

3.2 Problem formulation

Based on the basic model introduced in(1),we investigate the problem of collaborative lasso learning in edge computing systems.Specifically,it is assumed that each IoT devicei∈{1,...,N}generate a set of data samplesDi={(xij,yij),j=1,...,Mi},wherexij∈Rndenotes a feature vector,yij∈R denotes the response variable ofxij,andMidenotes how many data samples are contributed byi.Then,we hope to find a distributed solution to address the following minimization problem:

wherew∈Rn,andb∈R.

4 Distributed lasso learning via ADMM

According to the problem formulation and our analysis presented above,it is inappropriate to take the centralized approaches[Kwon,Hodkiewicz,Fan et al.(2016);Spencer,Alfandi and Al-Obeidat(2018)]as a solution in edge computing scenarios.A desirable solution should take the requirements on scalability,performance and privacy into consideration.This motivates us to develop an efficient and scalable scheme that enables collaborative lasso learning in a distributed manner.

4.1 A briefing on ADMM

The proposed scheme is based on ADMM,which follows a decomposition-coordination process.The target optimization problem is firstly decomposed into a set of small subproblems,and then the solutions to these sub-problems are coordinated to obtain the global optimal result.Specifically,ADMM solves optimization problems taking the following forms:

wherex∈Rn,y∈Rm,fandgare two convex functions,A∈Rl×nandB∈Rl×mare relation matrices,C∈Rlis a relation vector,andXandYare non-empty convex subsets ofRnandRm,respectively.

The augmented Lagrangian of problem(4)is formed by adding al2norm penalty to the objective function:

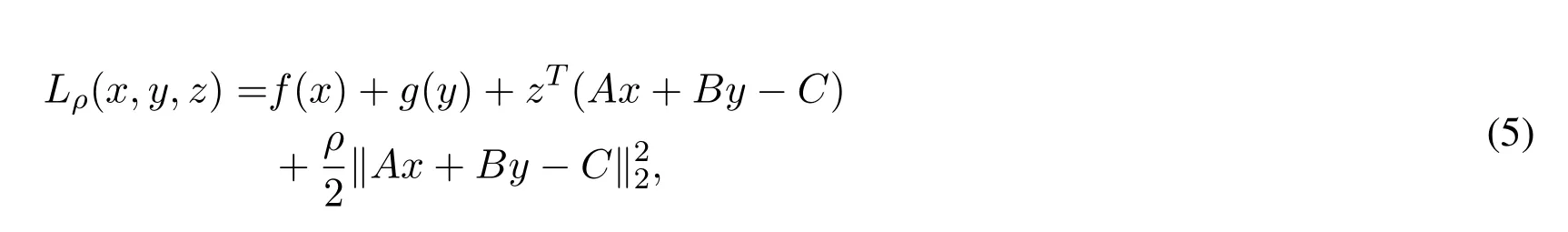
wherez∈Rlis the dual variable,andρis a positive penalty parameter.

Then,the problem(4)is solved in a iterative fashion,by updatingx,y,zsequentially and alternatively.Specifically,in thet-th iteration,the updates of variables are as follows:

The proofs on optimality and convergence of ADMM have been given in Bertsekas et al.[Bertsekas and Tsitsiklis(1989)].Besides,it is revealed by empirical studies that this technique often achieves an acceptable solution with modest accuracy after dozens of iterations[Boyd,Parikh,Chu et al.(2011)].

4.2 Algorithm design

However,ADMM cannot be applied to problem(3)directly,as the coupling of variables makes it impossible to separate the objective function over each set of variables.In this case,a set of auxiliary variables{(wi,bi),i=1,...,N}are introduced to reformulate problem(3)as:

By enforcing equality constraints,the new problem(7)is obviously equivalent to the original problem(3).Particularly,{(w,b)}can be regarded as the global model parameters at the edge server,while{(wi,bi),i=1,...,N}can be regarded as the local model parameters at each IoT devicei.Now we are able to separate the objective function over{(w,b)}and{(wi,bi),i=1,...,N}.The augmented Lagrangian of problem(7)can be obtained as:

where for simplicity we defineξ={(w,b)},ψ={(wi,bi),i=1,...,N},andζ={(ζi,w,ζi,b),i=1,...,N}as the dual variables associated with the equality constraints in(7).The problem is then solved by updatingξ,ψ,andζsequentially.In each iterationt,the updates are performed as follows:

1. ξ -update:The update ofξis performed by solving the following subproblem:

Since problem(10)is convex but non-differentiable,we use the subgradient calculus technique[Nesterov(2013)]in convex analysis to obtain a closed-form solution.The solution is given by

2. ψ -update:The update ofψis performed by solving the following subproblem:

This problem is decomposable intoNsubproblems over all IoT devices,among which the deviceionly needs to solve its local subproblem as follows:

The new subproblem(14)is a typical nonlinear programming problem,which is difficult to solve due to its complexity.Even standard tools like YALMIP can be used as solvers,they are still too heavyweight to run on IoT devices.Thus,we propose to to solve subproblem(14)by using the conjugate gradient method[Nesterov(2013)]in two sequential steps.Firstly,we consider the objective function of(14)as a functionhofwi,and letbi=btito find the optimalwi∗that minimizesh.Then,we consider the objective function of(14)as a functionh′ofbi,and letwi=w∗to find the optimalb∗that minimizesh′.After these two steps,we obtain the solution asDue to space limitations,we only introduce the algorithm forwi∗in Algorithm 1,whileb∗ican be obtained in a similar way.In Algorithm 1,kdenotes the iteration time,pdenotes the conjugate direction,εdenotes the convergence criteria.Particularly,we design a simple heuristic to search for the optimal step sizeσfrom a given setS,with the help of two auxiliary parameterss1ands2[Hager and Zhang(2006)].That’s because the objective functionh(wi)does not contain a symmetric and positive-definite matrix, which is required by standard conjugate gradient for determining the value of σ [Nesterov (2013)].Algorithm 1 presents the parameter values used in our experiments in Section 3.Note that the choice of suitable values for these parameters depends on the scale of variable values inh(wi).

Algorithm 1 Conjugate gradient algorithm for obtaining w∗i 1:Initialize k←0,ε←10-5,w0i←0,p0←-▽h(w0i),S←{-1,1},s1←1×10-2,and s2←2×10-2.2:repeat 3: σk←s1 4: for each δ∈ S do 5: if h(wi+δs2pk)＜ h(wi+σkpk)then 6: σk← δ 7: end if 8: end for 9: wk+1 i ←wki+σkpk 10: βk← ‖▽h(wk+1 i)‖2‖▽h(wki)‖2 11: pk+1=-▽h(wk+1 i)+βkpk 12: k←k+1 13:until Convergence:‖▽h(wki)‖ ≤ ε 14:w∗i←wki

3. ζ -update:After obtainingξt+1andψt+1,we finally update the dual variables as:

The entire process of algorithm execution in our scenarios is summarized in Algorithm 2.In this work,the primal residualrand the dual residuals[Boyd,Parikh,Chu et al.(2011)]are used together as convergence criterion,and they are expected to be less than their respective tolerancesєpriandєdual.According to Boyd et al.[Boyd,Parikh,Chu et al.(2011)],єpriandєdualcan be reasonably chosen using an absolute toleranceεabsand a relative toleranceεrel.In each iteration,a participating device submits locally trained intermediate parameters(wi,bi)and(ζi,w,ζi,b)to the edge server.The edge server then computes and updates the global model parameters(w,b)by averaging the parameters gathered from devices.The edge server and IoT devices work in such a collaborative way for multiple iterations until the lasso model converges.Note that in the above process,all training samples are kept locally at the device’s side,and protected from leakage to the edge server or other devices.

Algorithm 2 Distributed lasso algorithm in edge computing b 0 ← 0.2:Each IoT device i initializes t← 0, ζ 0 1:The edge server initializes t← 0, w 0 ← 0, i,w ← 0, ζ 0 i,b← 0.3:repeat 4:Given(w t b .According to(11)and(12),the server updates w t +1 and b t +1,and broadcasts the results to all devices.5:Given w t +1and b t +1,each device i solves the subproblem(14)independently to obtain w t +1 i)and(ζ ti,w ,ζ ti,b)from each device i ∈ { 1 ,...,N} ,the edge server computes w t,b t,i,b t ζ t w ,and ζ t i and b t +1 i .6:Each device i updates its dual variables ζ t +1 i,w and ζ t +1 i,b according to(15)and(16).7:Each device i sends the results of(w t +1 i ,b t +1 i)and(ζ t +1 i,w ,ζ t +1 i,b)to the edge server.8: t←t +1 9:until Convergence: ‖r t ‖2 ≤ ε pri and ‖s t ‖2 ≤ ε dual

5 Performance evaluation

In this section,we conduct simulation experiments to evaluate the performance of our ADMM-based algorithm.

5.1 Experiment settings

We evaluate our algorithm on two datasets,i.e.,a synthetic one and a real-world one.The synthetic dataset contains1500data samples,each of which includes nine dimensional feature vector.The generation of data follows the description in Boyd et al.[Boyd,Parikh,Chu et al.(2012)].Using this dataset,we can focus on evaluating the algorithm performance under different parameter settings,regardless of the impact of data quality.The experiment results are shown in Figs.1-4.Then,we use a well-known diabetes dataset from[Efron,Hastie,Johnstone et al.(2004)]to further investigate the algorithm performance under realistic conditions.This dataset contains442data samples,each of which includes ten dimensional feature vector.The experiment results are shown in Fig.5.In all experiments,we split the given dataset into70%training data and30%validation data.Unless otherwise specified,the simulation parameters are given as follows:N=10,λ=1.0,ρ=1.0,εabs=0.2,andεrel=0.5.

To provide performance benchmarks for the proposed algorithm,we compare it with two baselines,namely centralized training approach and independent training approach.As stated in Section 1,the centralized approach generally canobtain theoptimal result,but suffers from problems of scalability,performance and privacy.In the independent approach,each participating device trains its own model independently with local data samples.This approach overcomes the challenges of scalability and privacy at the cost of modeling performance,and the result accuracy is highly correlated with both the size and the quality of the training set.

5.2 Experiment results

Convergence of our algorithm.Fig.1 depicts the convergence property of our ADMM algorithm.The left-hand plot(Fig.1(a))shows the change of objective function value w.r.t.iterations,while the right-hand plot(Fig.1(b))shows the progress of the primal and dual residual norm w.r.t.iterations.The objective value computed using the centralized algorithm is taken as the global optimal result.As shown in Fig.1,we observe that our algorithm approaches very close to optimum after30iterations,and finally converges within 58iterations according to the given stopping criterion.

Figure1:Convergence of the ADMM-based algorithm

To fully investigate the convergence performance,we conduct random independent experiments for11times to compare the number of iterations for achieving convergence.As shown in Fig.2,our algorithm takes at most138iterations to converge,and the fastest run only takes17iterations.For80%of the time,our algorithm achieves convergence within 120iterations.On the other hand,the centralized algorithm takes at least580iterations to converge,and even800iterations in the worst case.These results clearly indicate that our algorithm converges significantly faster than the centralized approach.

Impacts of parameter settings.Next we study the algorithm performance under differentN,ρ,andλvalues(with other parameters fixed).All these results are plotted in Fig.3.As shown in Fig.3(a),our algorithm can always converge to the same optimal objective value no matter how many IoT devices are involved.We can observe that with the increase ofN,our algorithm converges with only moderate increment of iterations.These observations demonstrate the scalability of this algorithm as well as its associated overhead for device coordination.Similarly,varyingρalso has little impact on the final optimization objective,as shown in Fig.3(b).However,a smaller value ofρtends to speed up the dual update and achieve a faster convergence.From Fig.3(c),we can see that changingλonly determines the expected optimization objective in(3),but has neglectable impacts on the convergence and its rate of the algorithm.

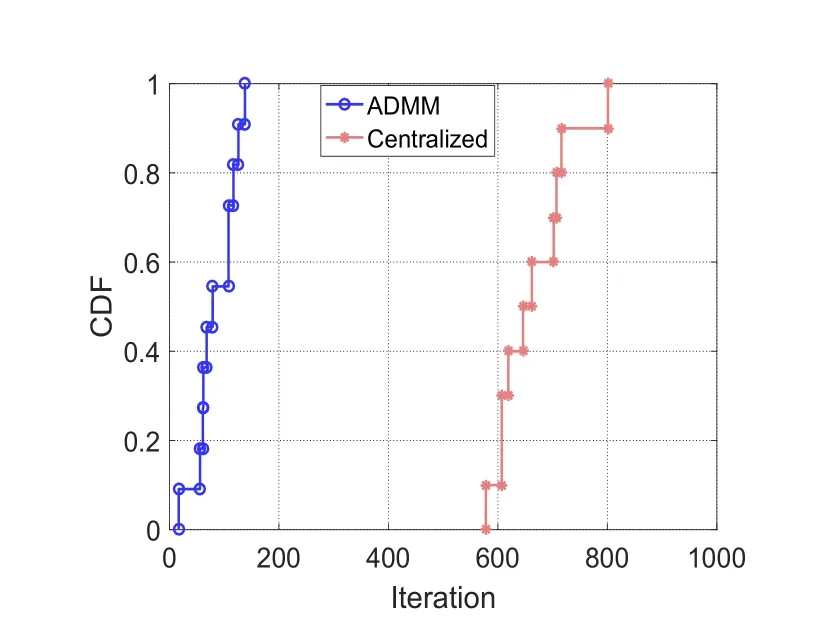
Figure2:CDF of the number of iterations to achieve convergence

Figure3:Convergence performance of the algorithm with varying parameter settings

Comparison of modeling performance.In order to evaluate model performance,we use the two most common metrics in regression analysis,including Mean Squared Error(MSE)and Adjusted R-Squared(Adjusted-R2)[Spencer,Alfandi and Al-Obeidat(2018);Kmenta and Rafailzadeh(1997)].MSE measures the expected squared distance between actual and predicted values.It must be non-negative,and a value closer to0indicates a better model.Adjusted-R2is used to measure the correlation between actual and predicted values.It can take on any value no greater than1,and a value closer to1indicates a better fit.Since the performance of the independent approach relies on the size of local training set,we randomly partition the original dataset intoNtraining subsets,and compare the performance of algorithms under different device numbersN.It is noted that whenN=1,the independent approach does actually equate with the centralized approach.

As shown in Fig.4(a),the average MSE of the independent approach keeps increasing with the increment ofN.The variance of MSE values also becomes larger asNincreases,implying that different IoT devices with same-sized data are more likely to obtain distinct training results.The MSE of our algorithm is always kept at about0.01,and does not depend onN.From Fig.4(b),we observe that our algorithm obtains a steady value of Adjusted-R2around0.985.The independent approach has a slightly better performance than ours whenN＜60,but its performance degrades significantly whenN≥60.An IoT device may even obtain a negative Adjusted-R2whenN=90,meaning that its resulting model doesn’t fit the data[Kmenta and Rafailzadeh(1997)].Note that for the centralized algorithm,MSE=0.000451and Adjusted-R2=0.998639.From these results,we know that the lasso models trained by the independent approach may not be robust for individual IoT devices,due to the limitation on data size and the lack of data diversity.Our algorithm can always converge to near-optimal and obtain modestly accurate models comparable to that of centralized approach,by utilizing data samples contributed by many IoT devices.

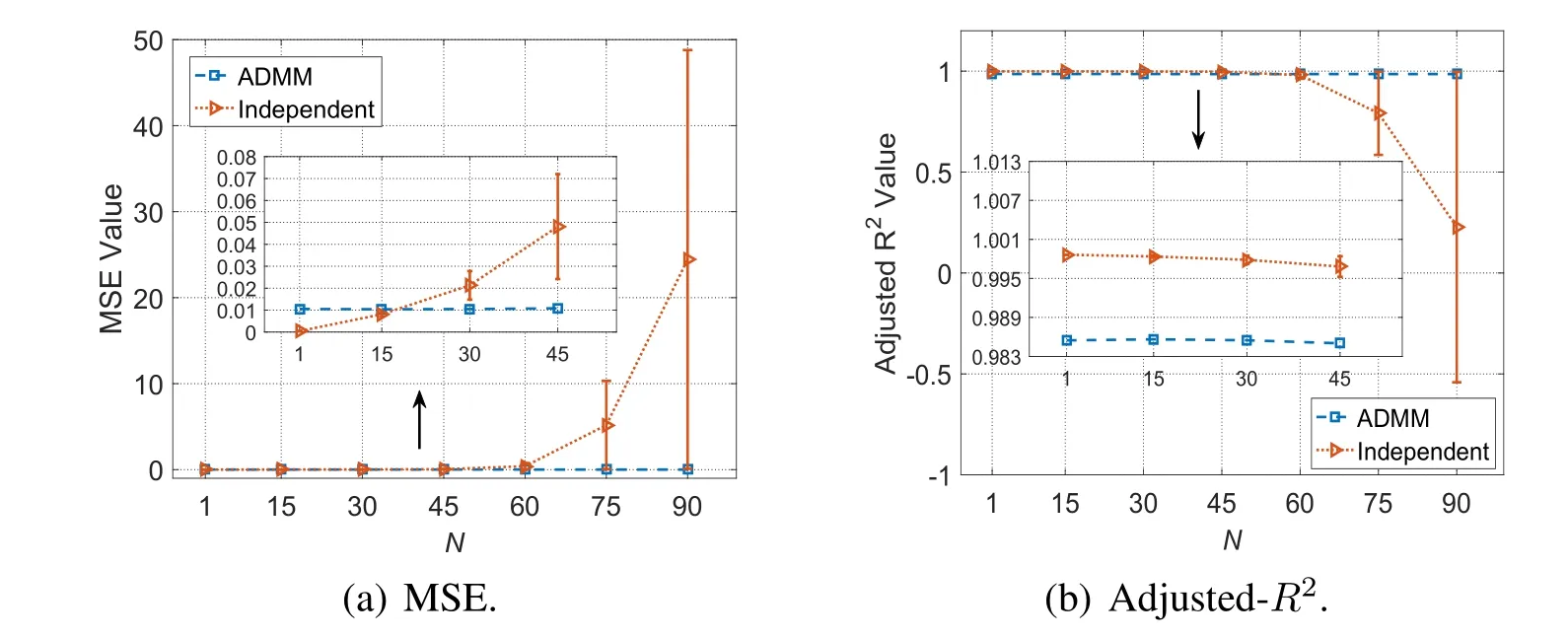
Figure4:Comparisons on model performance of different algorithms using different metrics

Results of real-world dataset.Furthermore,we evaluate our algorithm on the diabetes dataset in Efron et al.[Efron,Hastie,Johnstone et al.(2004)]using the same metrics.Due to space limitation,typical experimental results are chosen to be plotted in Figs.5(a)-5(c),respectively.

We obtain some new observations that are different from those presented above and need special attention.Firstly,as shown in Fig.5(a),the objective value of our algorithm falls off spectacularly fast during the initial 3 iterations,and converges after 25 iterations.We attribute this fast convergence rate to the significantly small size of this dataset.Secondly,the performance of the independent approach is obviously the worst among all three algorithms,according to Figs.5(b)and Fig.5(c).We can notice that start fromN=10,its MSE increases sharply to values far greater than0and those of other algorithms.Meanwhile,its Adjusted-R2decreases quickly and directly to negative values.These observations in-dicate that when training data are irregularly distributed overall,which is very common in reality,a good model is hardly to obtain by individual devices due to the severe lack of data diversity.Thirdly,our algorithm still achieves a good modeling performance comparable to that obtained by centralized approach.

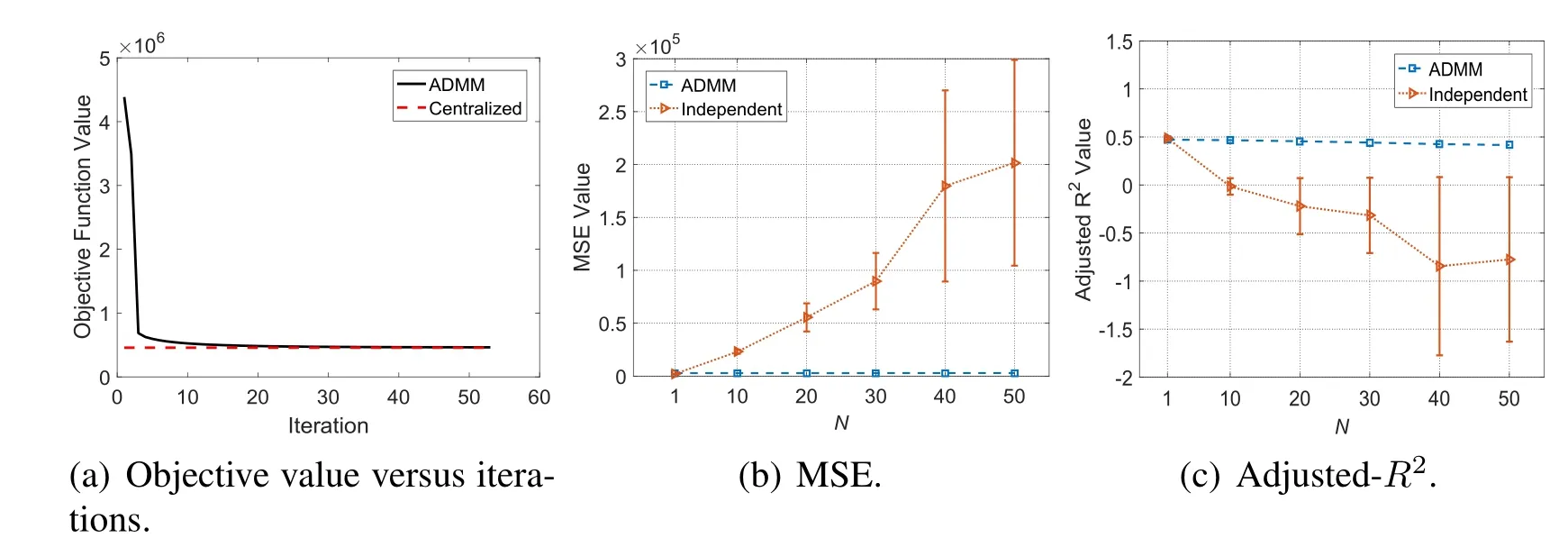
Figure5:Experimental results on the diabetes dataset

6 Conclusion

In this paper,we present a collaborative learning scheme for training lasso regression models based on data samples from IoT devices in edge computing.The target optimization problem of lasso is solved in a distributed fashion by leveraging ADMM,while the participating devices only need to share indispensable intermediate results with the edge server for model training.Simulation results on two typical datasets demonstrate that the proposed scheme can quickly converge to near-optimal within dozens of iterations,and significantly outperforms other baseline solutions in performance evaluation.Our future work involves implementing our scheme on a real edge computing platform to evaluate its feasibility and performance.