储能飞轮的转子动力学分析与测试试验

彭 龙，李光军，崔亚东，王 芳

（1北京泓慧国际能源技术发展有限公司，北京101300；2北京航空航天大学，北京100191）

飞轮储能技术是通过电动/发电机将飞轮机械能与电能相互转化的技术，具有充电时间短、响应速度快、能量密度较高、使用寿命长、环保无污染等优点[1-2]。随着高强度复合材料、大功率电动/发电机、磁悬浮、真空和电力电子等技术的发展，飞轮储能技术目前已经在电网调频、电能质量控制、卫星储能/姿态控制、车辆制动能量回收、不间断电源和高功率脉冲电源等领域获得了广泛的应用[3-7]。近年来我国在飞轮储能关键技术方面有所突破，部分大学和科研机构已经完成飞轮储能系统试验装置或工程样机的研制[8-10]。

飞轮转子技术与磁轴承技术一直是飞轮储能的关键技术[9]。本文以某公司的250 kW/3 kW·h 储能飞轮产品为研究对象，利用转子动力学理论与有限元仿真的方法分析，对储能飞轮的转子运动特性进行研究，通过对储能飞轮转子运动过程中的振动测试试验来验证分析结果的正确性。

1 转子系统分析理论基础

1.1 Timoshenko 梁理论

转子动力学有限元法能对大型复杂转子系统直接列出运动方程，考虑更复杂的边界条件和更多的内部影响因素。有限单元法常将轴段用连续梁来描述，不同的梁模型对高速旋转机械的动力学响应分析结果会有较大的影响。Timoshenko 梁理论考虑了剪切变形和转动惯量的影响，能准确分析转轴的高阶横向振动模态，被广泛应用在旋转轴的分析计算中[11-12]。

本文采用基于Timoshenko 梁理论的有限元法计算转子的临界转速及振动模态。图1 为Timoshenko模型，运动方程包含剪切变形、转动惯量、陀螺力矩，在复坐标中可写成式(1)形式[13]

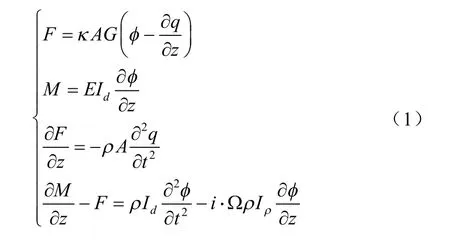
式中，q、φ为复横向位移和截面偏转角位移，q=x+iy，φ=θx+iθy；F和M为复剪切力和弯矩，F=Fx+iFy，M=Mx+iMy；ρ、E及G分别材料的密度、弹性模量及剪切模量；A、Iρ及Id分别为截面积、极转动惯量及直径转动惯量，κ为Timoshenko 剪切系数。剪切系数κ对Timoshenko 旋转梁的振动分析结果有很大影响，其大小与材料特性和截面几何形状有关[14]，对圆截面κ=6(1+μ)2/(7+12μ+4μ4)。

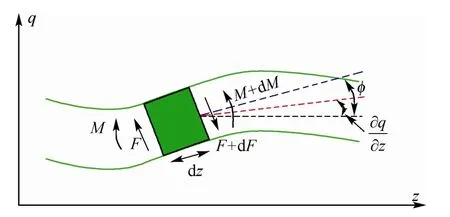
图1 Timoshenko 梁Fig.1 Timoshenko beam

1.2 转子单元运动方程

采用如图2 所示的弹性轴段单元来离散化转子，该单元的广义坐标是两端节点的位移，仅考虑横向振动时，单元位移向量包括4 个位移和4 个转角

引入Timoshenko 梁的典型位移函数[15]：

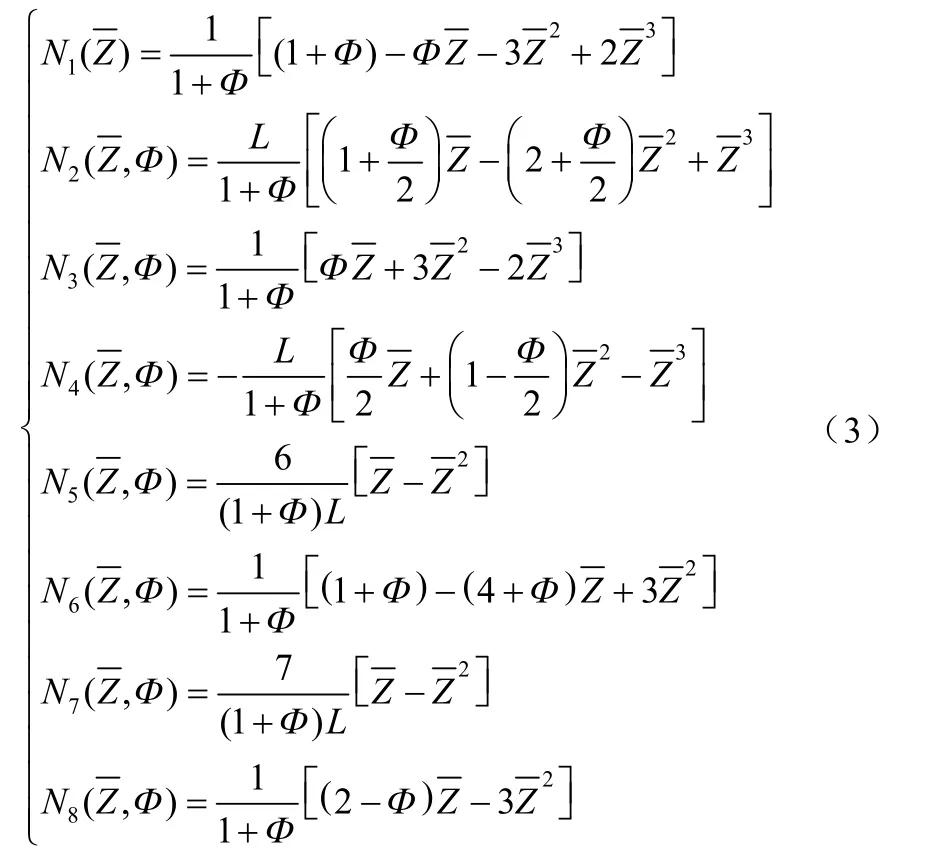
式中，EI为梁的弯曲刚度，κGA剪切刚度。

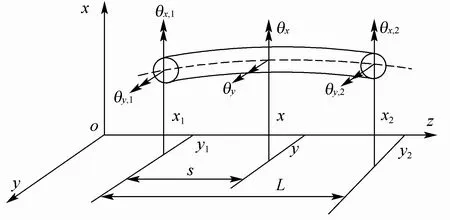
图2 轴单元Fig.2 Shaft element

轴段单元内任一截面的位移用该单元的节点位移表示为

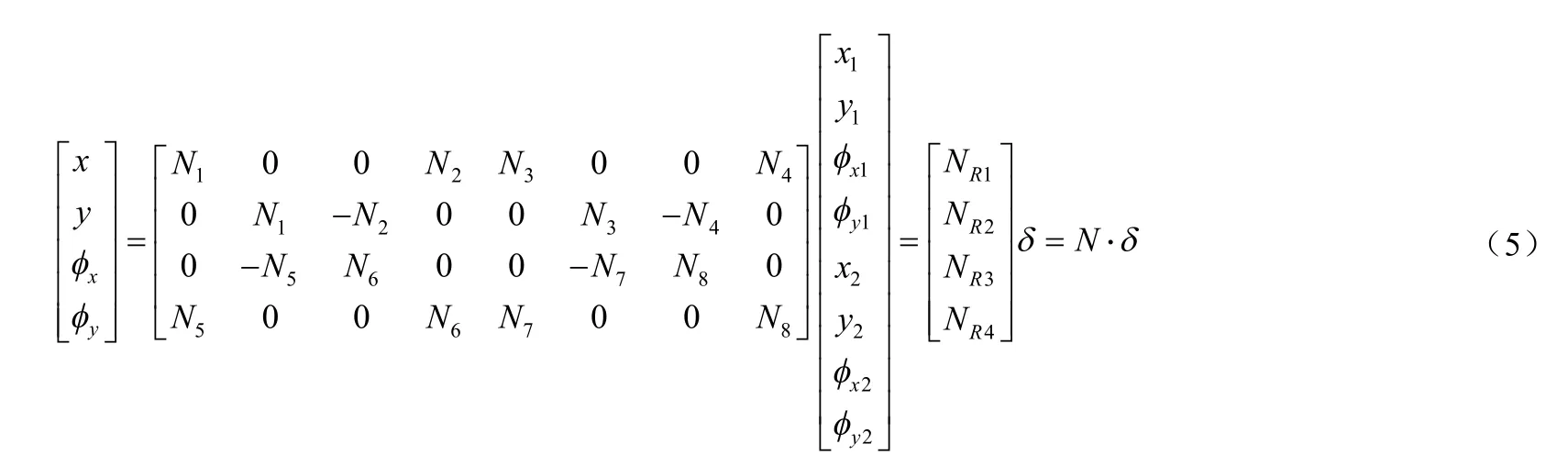
只考虑轴段的横向振动，且转子轴段截面为对称圆截面，则在固定坐标系中的动能和势能表达式为

将式(5)代入上边两式的

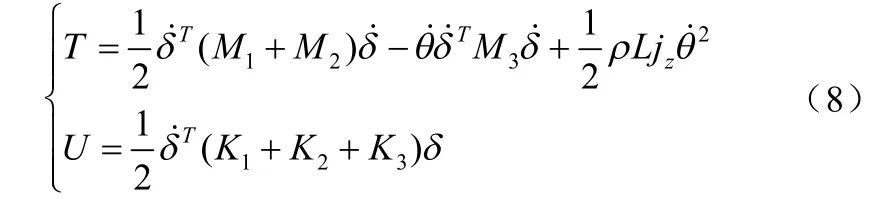
忽略轴段内阻尼将(8)式代入Lagrange 方程，可得轴段单元运动方程[16]

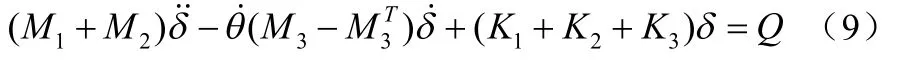
式中

2 转子动力学有限元分析

2.1 临界转速计算

250 kW/3 kW·h 储能飞轮转子组件，转子长1400 mm，最大直径600 mm，转子为单圆盘偏置结构，两端由金属叠片组成的磁悬浮轴承支撑部位。飞轮的额定工作转速为5000～9000 r/min。利用ANSYS 有限元分析软件，建立转子的有限元模型，采用轴对称实体单元SOLID272 划分网格，设置圆周方向上的傅里叶节点数为12，两端用COMBIN14单元支撑，如图3 所示。飞轮转子两端磁轴承支撑位置，通过利用弹簧单元等效磁轴承的弹性支撑形式，支撑刚度为5×105N/m。通过APDL 编程进行转子临界转速的求解。通过对转子施加0～20000 r/min 的转速。打开柯氏效应（coriolis effect），采用reduced damped 方法提取前4 阶模态频率与振型，并绘制坎贝尔图（Campbell diagram）如图4所示，进而求得飞轮转子的临界转速与振型。涡动频率曲线与转频的直线（斜率为1）的交点为临界转速。计算不同刚度下转子的一阶、二阶、三阶临界转速。见表1。

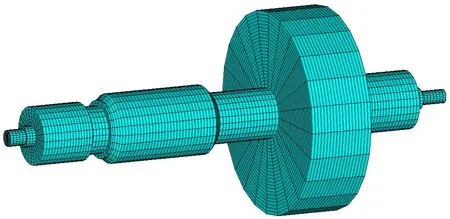
图3 飞轮转子有限元模型Fig.3 FE model of flywheel rotor

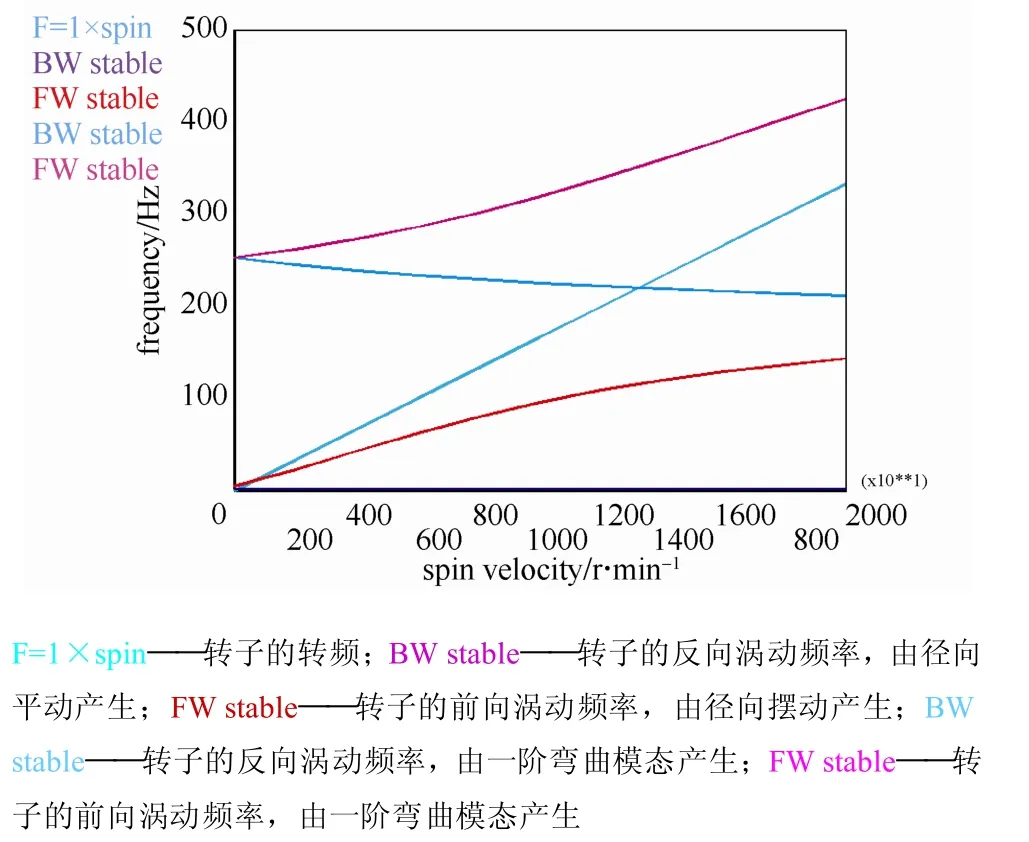
图4 Campbell 图Fig.4 Campbell diagram

表1为磁轴承刚度对临界转速的影响，随着磁轴承的刚度增加，转子的临界转速也在增大。可利用调节磁轴承的刚度以调整转子的固有振动频率，避开有害共振。

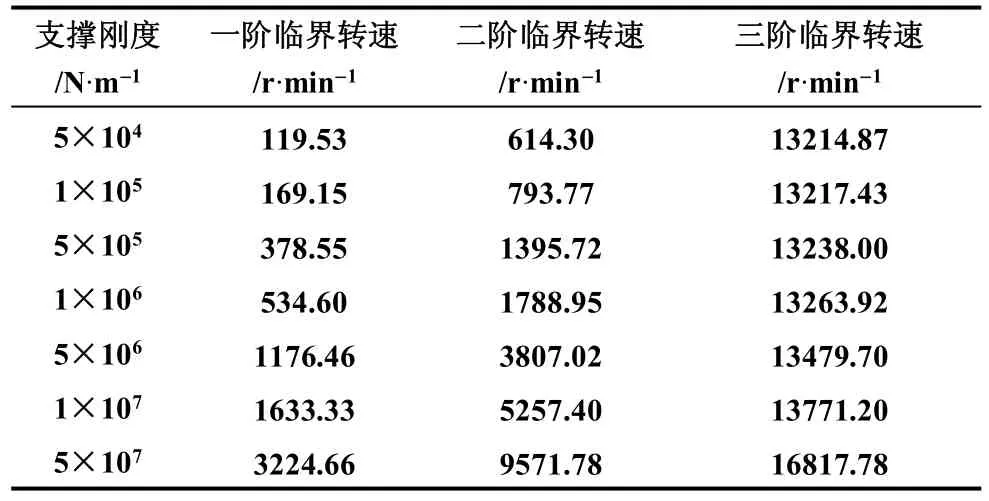
表1 临界转速的计算Table 1 The calculation of the critical speed

实际表明，磁悬浮轴承控制柔性转子的困难很大[16-17]。这是因为一般磁悬浮轴承的刚度要比滚动轴承小1～2 个数量级，而且控制参数的稳定域限制了磁悬浮轴承的刚度阻尼的变化范围。因此磁悬浮控制是有限的，为了避免这个问题，要求磁轴承支撑的为刚性转子结构，即额定转速下无弯曲模态临界转速。

通过转子的一阶临界转速对应的振型（图5）可以看出转子在做径向的平动，左端位移小，右端位移大，这是由于转子的平动模态产生。转子的二阶临界转速对应的振型（图6）是由于转子的摆动模态产生的径向的摆动，基本以圆盘为中心，左端偏离距离大于右端。图7、图8 分别表示转子在两个不同方向的一阶弯曲模态的振型，在坎贝尔图中，分别对应的是由一阶弯曲模态产生的转子的反向涡动频率与正向涡动频率。如图4 所示，在20000 r/min的转速范围内，转频与一阶弯曲模态产生的反向涡动频率曲线相交，为三阶临界转速，振型如图7所示。

图5 转子平动模态振型Fig.5 Rotor translation mode

图6 转子摆动模态振型Fig.6 Rotor vibration mode

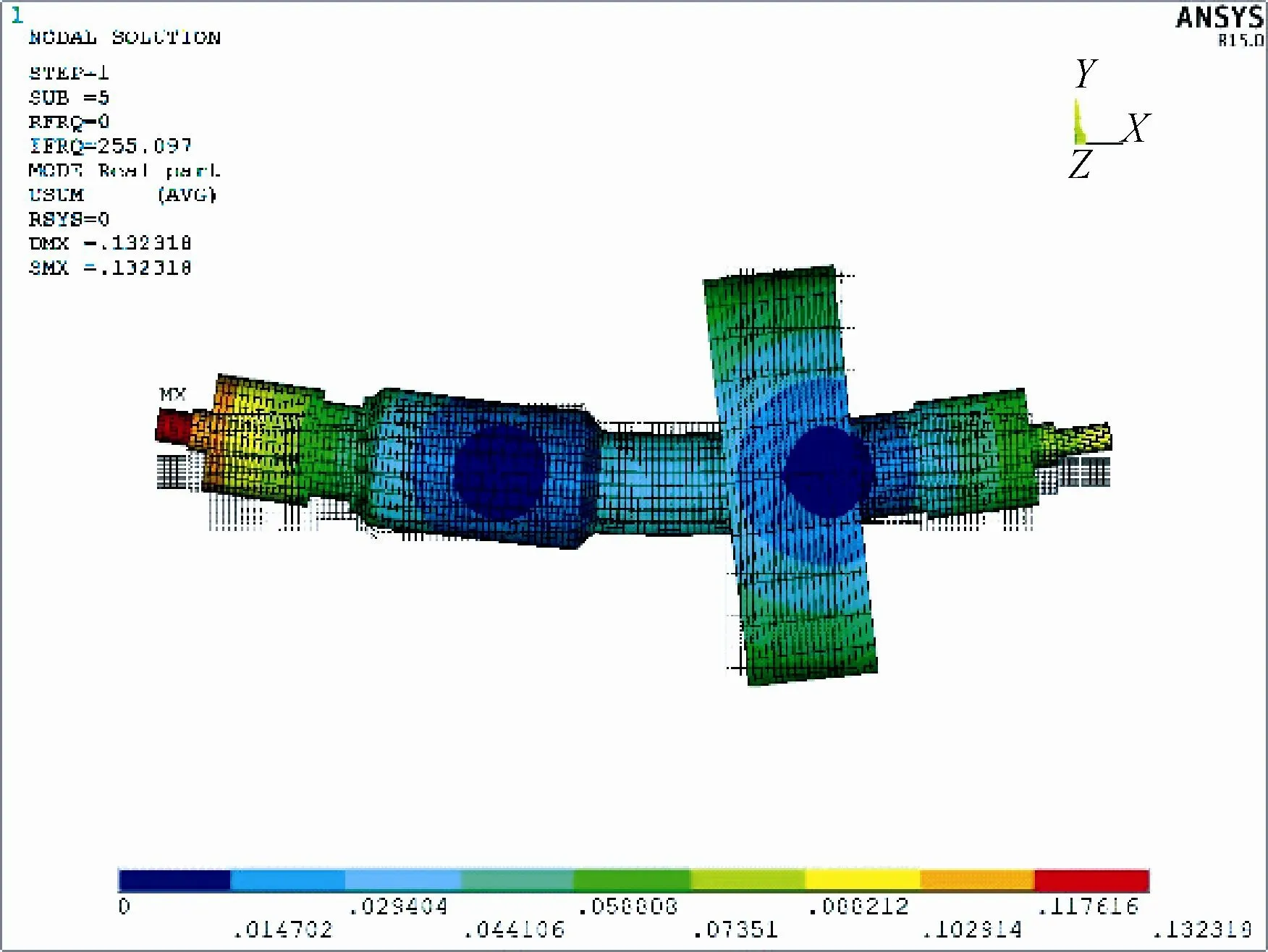
图7 转子一阶弯曲模态振型（oxz 平面）Fig.7 First order bending mode of rotor（oxz plane）

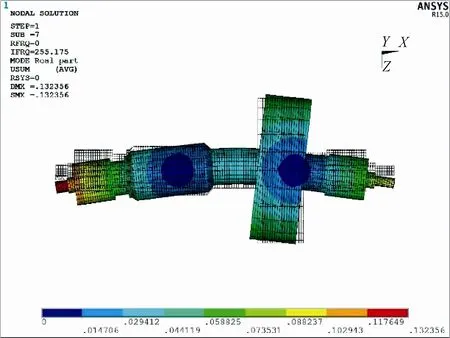
图8 转子一阶弯曲模态（oyz 平面）Fig.8 First order bending mode of rotor（oyz plane）

通过临界转速所对应的振型可以看出转子的一阶、二阶临界转速为转子刚性振动，三阶临界转速为转子弯曲的柔性振动。储能飞轮设计时，工作转速范围应避开一阶、二阶刚性临界转速，且不超过第三阶弯曲临界转速。由于在临界转速附近一定范围内也会引起振动，所以在实际设计中转子的最高工作转速应小于0.7 倍的弯曲临界转速，才能保证转子为刚性转子，避免受到临界转速的干扰。

储能飞轮的最高工作转速为9000 r/min，小于计算得出的第三阶弯曲临界转速13238 r/min 的0.7倍，因此飞轮的转速设定是合理的。

2.2 不平衡响应的计算

转子模型采用了BEAM188 单元建模，使用COMBIN214 单元支承转子，支承刚度为1×106N/m。在转子中心施加1.88×10-4N 的不平衡力。利用完全法对转子不平衡响应进行谐响应分析。设置不平衡力的激励与转子转频同步，指定执行加载步骤的子步骤数为500，定义了谐波分析的频率范围为0～500 Hz，通过命令打开科里奥利效应，然后进行求解。绘制出在0～500 Hz 转频内不平衡量激励下的转轴上三点（上径向磁轴承支撑位置、转子中心位置、下径向磁轴承支撑位置）的位移响应图，如图9 所示。

图9 不平衡力激励下的转子轴的位移响应图Fig.9 Displacement response diagram of rotor bearing under excitation of unbalanced force

在不平衡力激励下的转轴出现三次明显波动，对应的频率分别为10.4 Hz、35.2 Hz、280.0 Hz，对应转轴的轨迹图分别如图10、图11、图12 所示。通过转轴的轨迹图可以看出，转子在不平衡力激励下产生的三次振动，与2.1 节中分析的三阶临界转速相对应。由表1 可知，在支承刚度为1×106N/m时，转子的临界转速分别为534.60 r/min、1788.95 r/min、13263.92 r/min（即8.91 Hz、29.8 Hz、221.06 Hz），与在不平衡力激励下的振动频率存在约20%的误差，主要原因是由于采用了BEAM188 单元求转动轨迹简化模型造成的。综上分析得出，在频率280.0 Hz 时是由一阶弯曲模态反向涡动引起的临界转速，在不平衡激励力作用下，在其临界转速附近具有较大的振动幅值，如图9 所示。通过对转子进行不平衡响应分析，验证了临界转速求解的正确性，并说明了一阶弯曲模态引起的临界转速在一定范围内都会引起转子的振动，在临界转速时达到峰值。

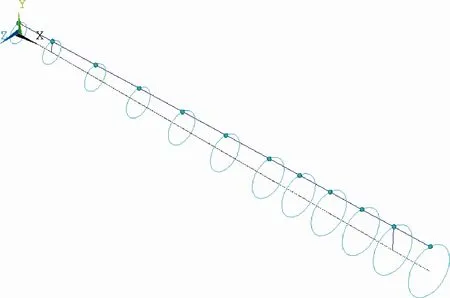
图10 转轴平动的轨迹图Fig.10 Trajectory chart of translation of spindle

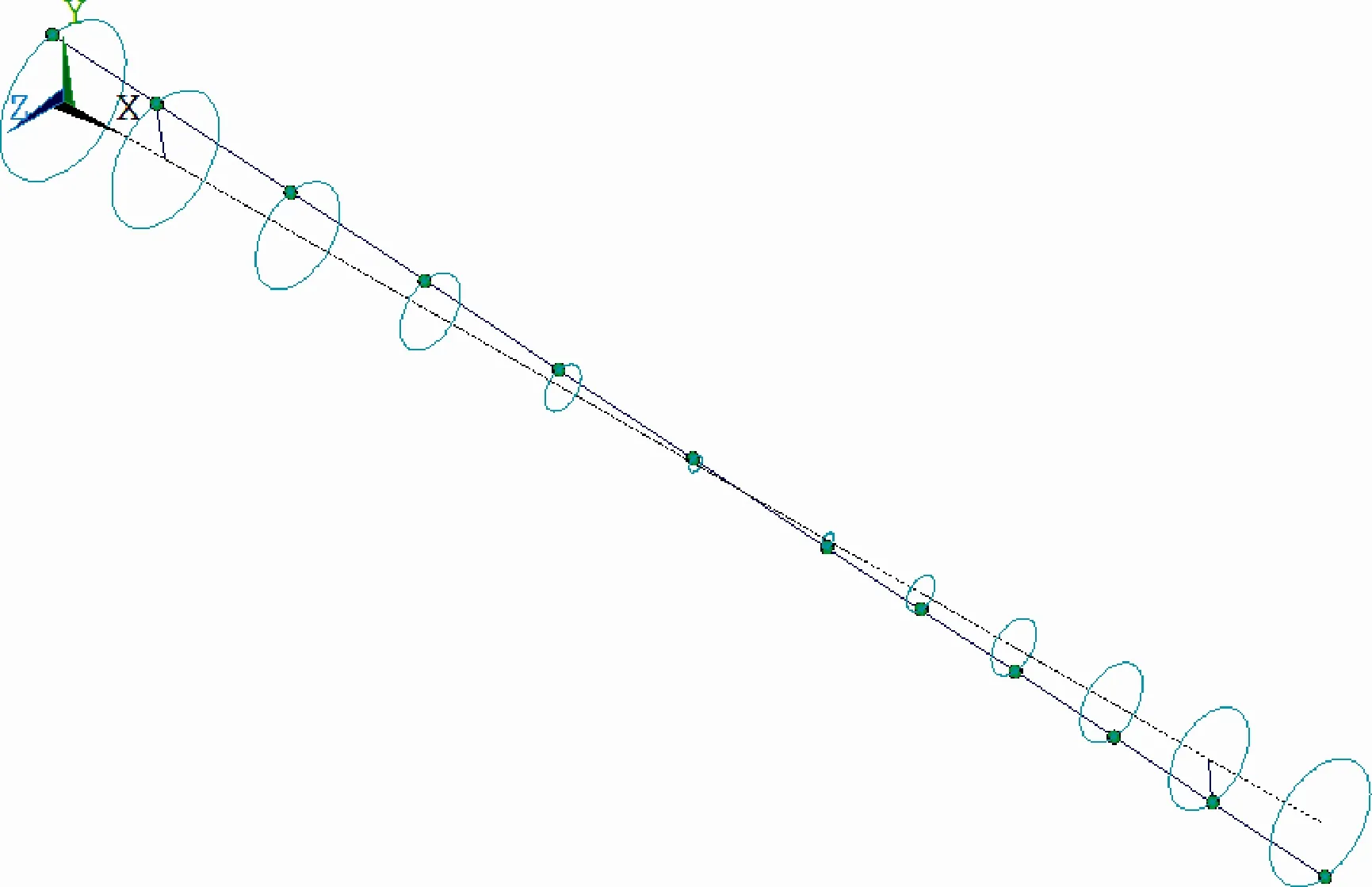
图11 转轴摆动的轨迹图Fig.11 Trajectory chart of axis swing

图12 转轴一阶弯曲的轨迹图Fig.12 Trajectory chart of first order bending rotation axis

3 飞轮测试

3.1 测试方法

250 kW/3 kW·h 的储能飞轮产品如图13 所示，它主要由储能飞轮本体、变频器、磁轴承控制系统、真空系统及主控系统组成。测试方法是在储能飞轮从0～9000 r/min 的升速过程中，利用径向磁轴承的电涡流位移传感器采集转子径向位移信号，通过磁轴承的控制器输出到示波器，每间隔200 r/min 存储一次位移信号的波形和频谱数据。然后利用MATLAB 绘制频谱的三维瀑布图，与仿真分析的Campbell 图进行对比分析。利用波形数据绘制出最大振动位移响应图与不平衡力下的转子位移响应图进行对比分析，通过对比分析结果来验证仿真分析的准确性。

图13 测试的储能飞轮产品Fig.13 The energy storage flywheel for testing

3.2 试验结果分析

由于飞轮转子是立式旋转，主要储能的圆盘位于转子偏下部位，在转子摆动时，上径向磁轴承位置的摆动幅值比较大，通过图6 能明显看出，所以采集上径向磁轴承Y向的转子振动位移数据进行分析，利用MATLAB 软件编程绘制了上径向磁轴承位置振动位移的频谱瀑布图，如图14 所示。

从图14中，明显能看出转子的转频及3倍转频，它主要是由不平衡量激励引起，还有由一阶弯曲模态而产生的正向涡动与反向涡动。与图4 的Campbell 图对比发现，由于储能飞轮结构部件模态响应及其他部件的影响，对采集的振动位移信号产生了许多低频干扰信号，致使转子的平动和摆动频率无法明显从图14 中明显看出，此点不足在下文中能通过对比振动位移曲线来进行分析验证。通过对比图4与图14能发现由一阶弯曲模态引起正向涡动频率和反向涡动频率曲线是完全一致的，证明了临界转速的分析结果与实际测试结果一致。

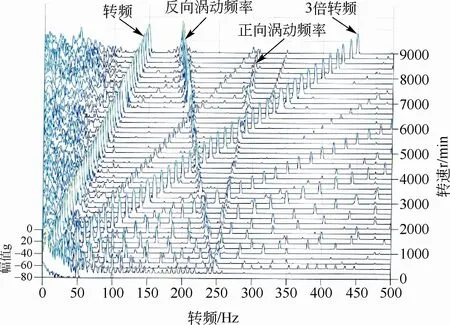
图14 频谱瀑布图Fig.14 Spectral waterfall chart

通过实测的上径向磁轴承Y向的转子振动位移数据，绘制出最大振动位移随转速变化的曲线，如图15 所示。从图9 中提取出在不平衡力的激励下上径向磁轴承支撑位置转轴的振动响应，如图16 所示。通过图15 和图16 的对比得出，在0～9000 r/min（0～150 Hz）范围内，实测与仿真分析出的曲线变化规律完全相同。在低转速下，出现了两次峰值，第一次峰值明显高于第二次峰值，然后曲线降低，趋近于平缓。通过不平衡响应仿真分析结果，可知实测曲线的两个峰值分别对应转子平动模态的临界转速与摆动模态的临界转速，验证了分析结果前两阶刚性临界转速的正确性。

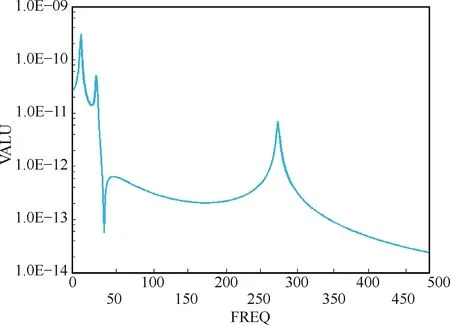
图16 上径向磁轴承支撑位置转轴的振动位移响应图（仿真）Fig.16 Vibration displacement response diagram of the support position of the upper radial magnetic bearing(simulation)

4 结 论

（1）利用ANSYS 软件仿真分析，绘制了250 kW/3 kW·h 的储能飞轮坎贝尔图，在不同支撑刚度下计算出转子临界转速，结果得出随着支撑的刚度增加，转子的临界转速也在增大。可利用调节主动磁轴承的刚度以调整转子的固有振动频率，避开有害共振。

（2）通过对转子进行不平衡响应分析，计算出了转子上不同位置的振动位移曲线，和每个临界转速对应的运动轨迹图，形象的展示了转子在临界转速时的运动形态，并且充分验证了临界转速求解的正确性。

（3）通过分析得出，储能飞轮的工作转速范围应避开前两阶刚性临界转速，且不能超过弯曲临界转速的0.7 倍。

（4）试验测试结果验证了仿真分析结果的正确性。说明了对250 kW/3 kW·h 储能飞轮的转子动力学设计的参数是合理的，满足产品的设计指标要求。