航天器刚性太阳翼在轨一维展开时间近似算法

苟仲秋 张永 王杰

(中国空间技术研究院载人航天总体部,北京 100094)

航天器太阳翼在轨展开是航天器发射成功的重要标志之一,为保障飞行任务成功,一般要求航天器入轨后太阳翼尽早在测控区内展开,以保证航天器上众多电子设备的供电。太阳翼展开时间与飞行方案的制定密切相关,是支持地面测控站布局的重要参数[1-2]。在航天器方案设计阶段就必须对太阳翼在轨展开时间提出明确指标。

航天器总体方案设计阶段,根据功率需求、轨道特性以及火箭整流罩等约束,确定所采用的基板尺寸、个数等主要太阳翼参数,对展开时间、基频等进行分析,评估太阳翼方案是否满足航天器总体的要求。太阳翼展开时间可通过多体动力学和有限元结合的数值解法获得[3-5],也可以通过太阳翼地面展开试验进行测定[6-9]。方案设计阶段由于要对多种太阳翼方案进行选择和优化,通过多体动力学和有限元结合的数值解法来获得太阳翼的展开时间,需要由相关专业人员建模分析,计算复杂,不便于航天器总体方案早期设计时工程应用;太阳翼产品投产前也不能通过太阳翼地面展开试验获取展开时间。因此,为航天器总体在方案设计阶段对太阳翼提出科学合理、便于工程应用的在轨展开时间指标,为总体方案选择提供快速、易用工具,开展航天器太阳翼在轨展开时间近似计算方法的研究具有重要意义。

文献[10]利用动-势能驻值原理,提出了固定太阳翼展开外弯模态基频的近似计算方法,但未给出太阳翼展开时间计算方法。文献[3-5]利用多体动力学和有限元结合的数值解法进行太阳翼展开时间分析,专业性强,工作量大。

本文以航天器一维展开刚性太阳翼为对象,将太阳翼的在轨展开运动简化为单自由度的刚性运动。利用动-势能守恒原理,推导太阳翼在轨展开时间的理论公式。根据实际工程参数对太阳翼在轨展开时间的理论公式进行简化、拟合,建立太阳翼在轨展开时间的近似算法。通过将近似算法解析计算的太阳翼在轨展开时间与数值仿真结果进行比对,验证近似算法精度满足工程要求(一般不大于20%)。

1 太阳翼在轨展开运动描述

以3块基板的太阳翼模型为例,太阳翼展开运动分析模型如图1,由连接架AB和内板BC、中板CD、外板DE组成,A、B、C、D为铰接点,其中A点与卫星本体铰接。太阳翼的在轨展开运动可视为单自由度的刚性运动,以图1中的连接架与最终展开位置的夹角φ作为自由度参数,它从π/2(收拢状态)变化到0(最终展开状态)。

太阳翼在轨展开运动分析时主要假设如下。

(1)太阳翼基板:假设每块基板的尺寸和质量特性相同,设其质量和惯量分别为mi＝M和Ji＝J,i＝1,2,…,n表示第i块基板;设A为太阳翼展开方向的基板尺寸,a为基板展开方向尺寸的一半,则

(2)太阳翼铰链:假设板间铰链的扭簧刚度均相同,根部铰链和板间铰链的扭簧刚度不同,设板间铰链扭簧刚度为Ks,根部铰链的扭簧刚度为Ks0。一般根部铰链和板间铰链的初始扭转角度差值并不确定,但在理论推导时,可以通过调整根部铰链的扭簧刚度进行等效简化,为了便于分析,将收拢状态根部铰链的扭簧初始扭转角度设为α－π/2,板间铰链的扭簧初始扭转角度设为α。

(3)太阳翼摩擦力矩:将太阳翼展开运动过中铰链阻力矩简化为一个“等效扭簧”的作用,设根部铰链阻力力矩刚度为Kr0,板间铰链阻力力矩的刚度为Kr。

(4)连接架:设其质量和惯量分别为m0和J0。考虑实际设计太阳翼连接架时,其展开方向的尺寸约为基板的一半,这里设a＝2a0(a0为连接架展开方向尺寸的一半)。

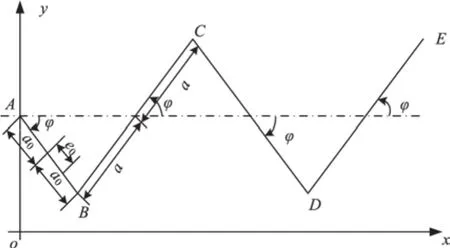
图1 刚性基板太阳翼简化模型Fig.1 Equivalent simplification model of rigid substrate solar wing

2 太阳翼在轨展开时间近似公式推导

对图1所示的太阳翼模型进行展运动分析。连接架的长度为2a0,质心偏心距为e0,n为基板个数,则连接架的质心坐标为

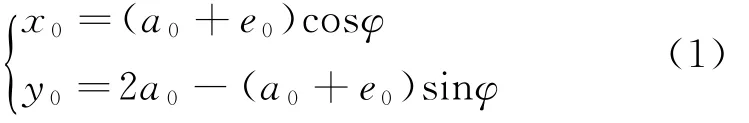
太阳翼基板的质心坐标为

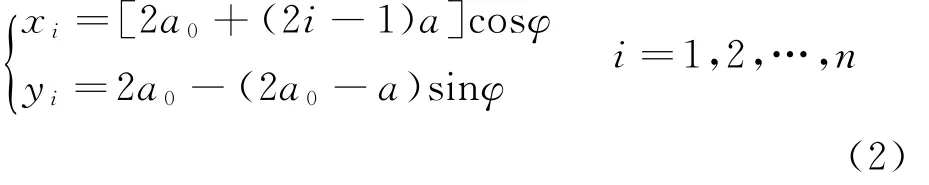
将式(1)、(2)对时间t作为一次微分,可以得

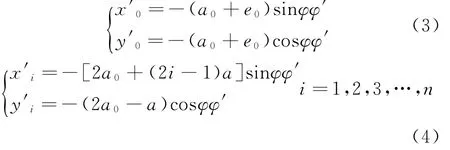
式中:φ′为φ对时间t的导数。

整个太阳翼系统的动能W可以表示为

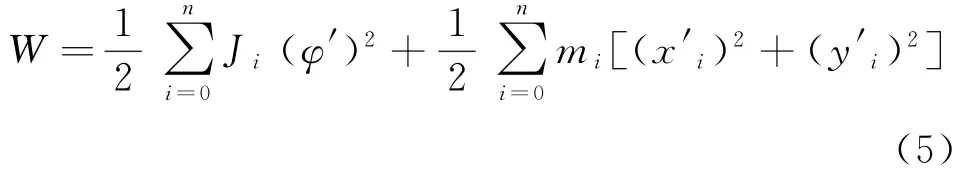
将式(3)、(4)代入式(5)中,并代入第1节假设中参数,可得

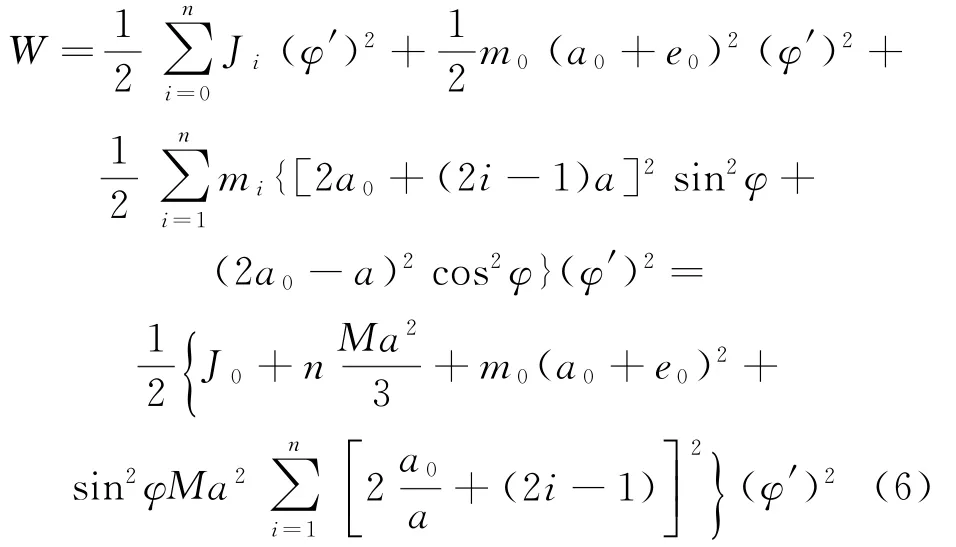
另一方面,系统的势能V可以表示为

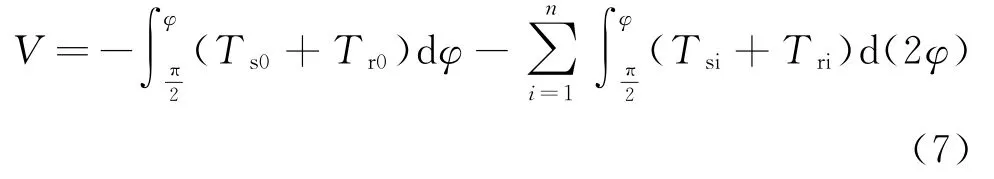
铰链扭簧力矩及其阻力矩可表示为

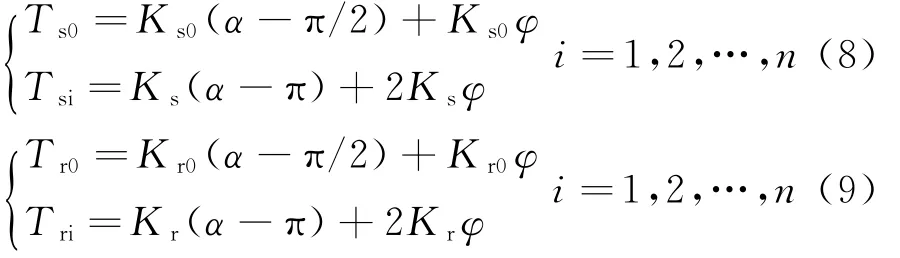
将式(8)、(9)代入式(7),得

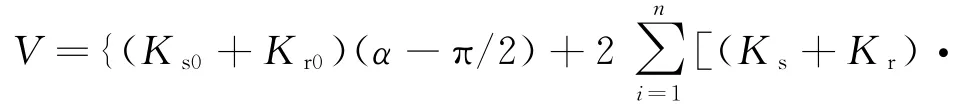
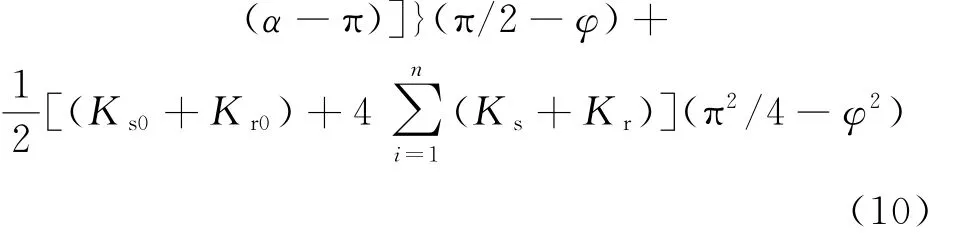
令K0＝Ks0＋Kr0,T0＝K0(α－π/2),K1＝Ks＋Kr,T1＝K1(α－π),定义弹簧常数的比例系数λ＝则式(10)可以简化为

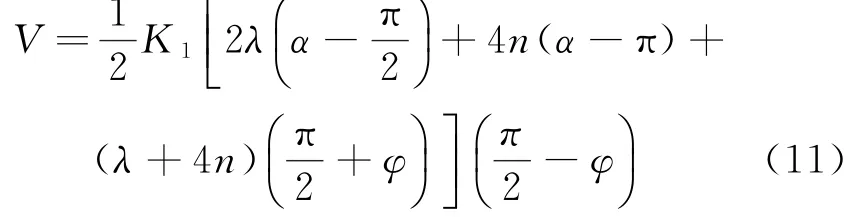
利用能量原理W＝V,将式(6)、式(11)代入,并定义转动惯量系数β,使得得到求解角速度的公式为

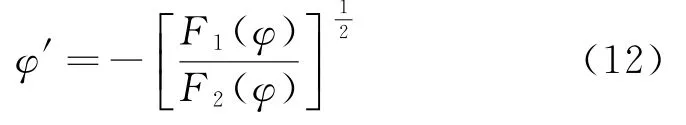
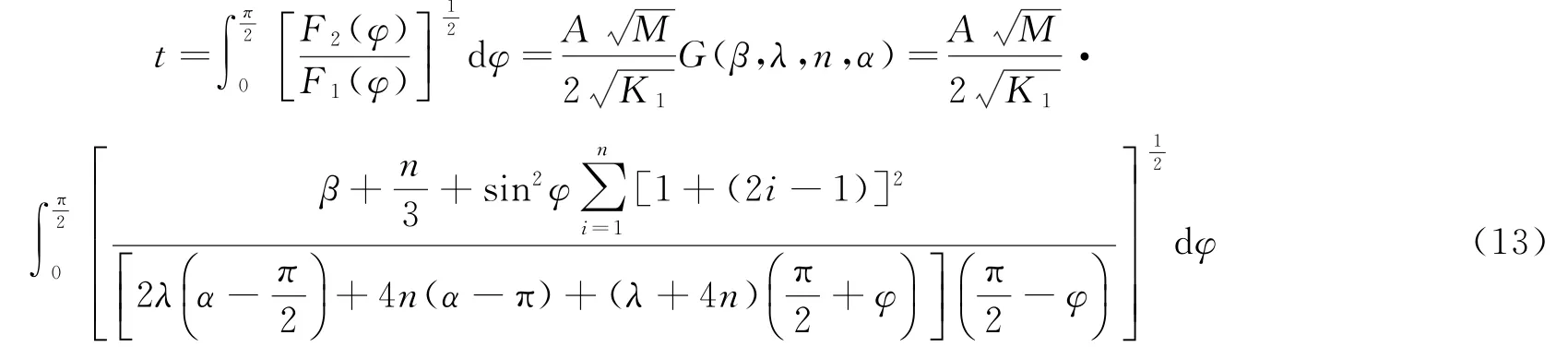
由式(13)可以得到t随φ的变化过程,当φ取0时,可得到整个太阳翼的展开时间。由于被积函数在φ＝π/2时趋于无穷大,因此实际的积分上限应取很接近π/2的值,而由此引起的计算误差极少,在工程上完全允许。

根据实际工程中采用的铰链参数,λ一般在2.5～3.5,其变化对展开时间G(β,λ,n,α)的影响不大,拟合时取λ＝2.8,连接架与基板的转动惯量系数β∈[0,1.1],扭簧初始扭转角度α选取范围为[1.5π,4.5π],基板个数n选取范围为[1,6];通过对G(β,n,α)进行数值拟合,即可建立太阳翼展开时间的工程近似式(14),其中修正系数βi用于对拟合误差进行修正。

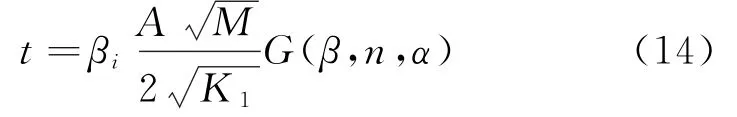
式中:G(β,n,α)＝[0.39121＋1.03512n＋0.68164·(1＋n)－1.76373β](1＋α/π)－0.73759,A为太阳翼展开方向的基板尺寸,M为太阳翼基板的质量,n为基板的个数,K1为太阳翼板间铰链的实际等效刚度,K1＝(Ks＋Kr),转动惯量系数一般选择βi＝1。

3 算例

以工程中使用的3种基板尺寸系列太阳翼进行近似算法验证,其基板尺寸分别为850 mm×1110 mm、2400 mm×1700 mm 和1755 mm×2581 mm。

假设铰链的K1＝0.753 5/π,α＝1.9π,在不同的基板个数的情况下,利用式(14)计算太阳翼的展开时间,并与ADAMS软件数值仿真结果比较,以验证式(14)精度。ADAMS数值模型中基板为刚体模型,铰链刚度设为相同的板间铰链等效刚度。

1)基板尺寸为850 mm×1110 mm

连接架的质量m0为1.05 kg,偏心距e0＝0.084 m,J0＝0.023 4 kgm2,系数β为0.244 5,基板质量为2.62 kg。近似公式计算与ADAMS数值仿真的太阳翼展开时间比较结果如图2所示。由图2可知,两者分析结果基本一致,β不大时,在确定的板间铰链等效刚度和基板质量特性条件下,展开时间随基板个数近似线性增加。

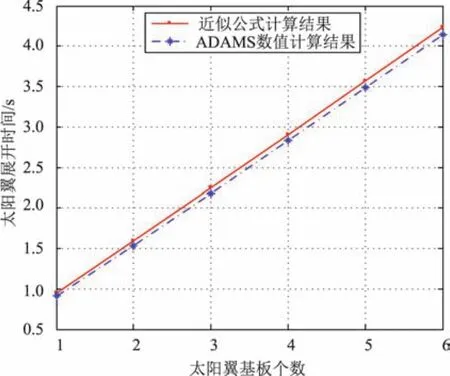
图2 近似公式计算与ADAMS数值仿真的太阳翼展开时间比较(850 mm×1110 mm基板)Fig.2 Deployment time of solar wing between approximate method and ADAMS(850 mm×1110 mm substrate)

2)基板尺寸为2400 mm×1700 mm

连接架的质量m0为2.34 kg,偏心距e0＝0.2 m,J0＝0.397 4 kgm2,系数β为0.133 3,基板质量为9.87 kg。近似公式计算与ADAMS数值仿真的太阳翼展开时间比较如图3所示,两者分析结果基本一致。进一步对比图2、图3,β不大时,相同基板个数的展开时间近似随线性变化。

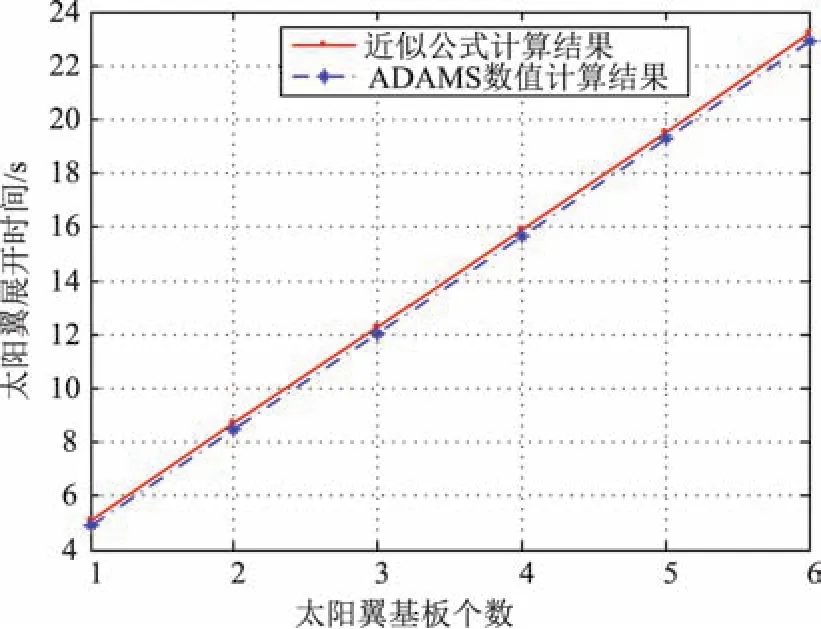
图3 近似公式计算与ADAMS数值仿真的太阳翼展开时间比较(2400 mm×1700 mm基板)Fig.3 Deployment time of solar wing between approximate method and ADAMS(2400 mm×1700 mm substrate)

3)基板尺寸为1755 mm×2581 mm

连接架的质量m0为2.457 kg,偏心距e0＝0.193 75 m,J0＝0.2167 kgm2,系数β为0.0929,基板质量为10.926 kg。近似公式计算与ADAMS数值仿真的太阳翼展开时间比较结果如图4所示。1755 mm×2581 mm基板尺寸的分析结果基本一致,β不大时,展开时间仍随基板个数近似线性增加。

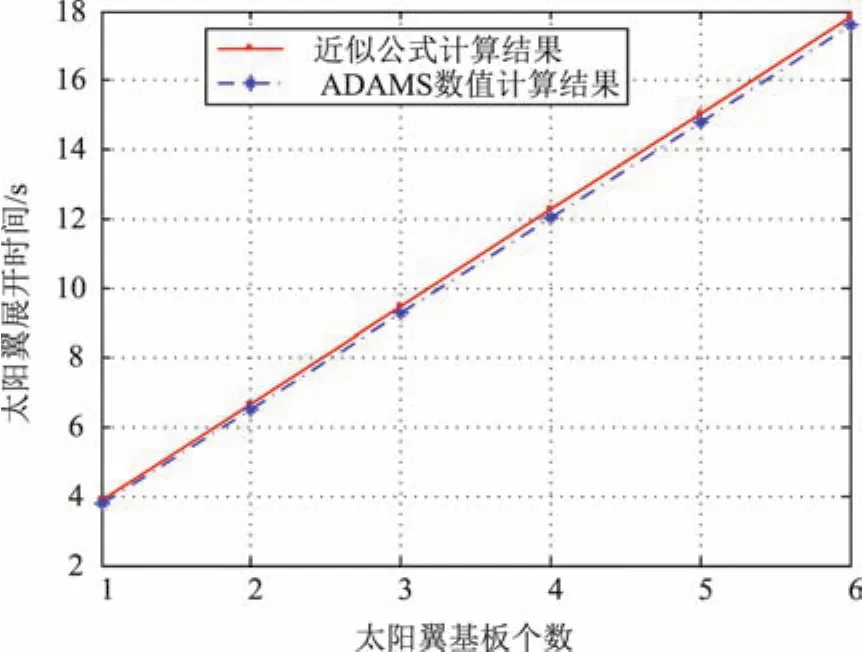
图4 近似公式计算与ADAMS数值仿真的太阳翼展开时间比较(1755 mm×2581 mm基板)Fig.4 Deployment time of solar wing between approximate method and ADAMS(1755 mm×2581 mm substrate)

由图2～4的比较结果可以看出:对基板尺寸不同的太阳翼,近似式(14)与ADAMS软件的数值分析结果相对误差均小于10%,可以满足工程精度的要求。

4 结束语

本文基于能量守恒原理,提出了航天器刚性太阳翼在轨展开时间近似计算方法,可利用基板数目、尺寸、质量以及板间铰链扭簧初始扭转角度、等效刚度、转动惯量等参数,解析计算刚性太阳翼在轨一维展开时间,相对数值仿真误差小于10%,可以满足工程要求。该方法可为航天器总体设计人员提供一个快速、易用的太阳翼在轨展开时间计算分析工具,有利于总体方案设计阶段对多种太阳翼方案进行迭代评估,合理确定在轨展开时间指标,提高航天器总体方案设计效率。