火星车定向天线自主对地指向规划方法
2019-05-10彭松贾阳隆昌宇陈百超朱玛张建利
彭松 贾阳 隆昌宇 陈百超 朱玛 张建利
(1北京空间飞行器总体设计部,北京 100094)(2北京卫星环境工程研究所,北京 100094)
中国将在2020年左右发射火星车进行火星表面巡视探测,由于遥远的地火距离,配置高增益、窄波束的定向天线进行对地数据传输是必需的。通常车载的面阵定向天线通过双轴机构进行驱动,以机构运动实现半球空间覆盖,如美国的 “火星探测巡视器”(MER)[1-2]、中国的嫦娥三号巡视器[3]等。定向天线的对地指向是一个关键的过程,在任务层面需要考虑能源、数据量、通信窗口、遮挡等因素[4];具体到双轴机构指向规划算法,除了机构本身的运动学模型、关节转动范围、遮挡分析外[5],还需考虑时刻、星历、火面位置、火星车姿态、天线安装执行误差等多因素的影响。在中国嫦娥三号探月任务中,工程人员提出了月球车的定向天线对地指向规划方法,地面规划完成后发送指令控制机构运动[6]。和月球车相比,火星车和地球之间的通信延时约3~23 min,不可能像月球车那样执行准实时的地面遥操作控制[7],所以火星车的定向天线对地指向需由器上自主实施,一方面器上要运行星历计算、机构指向计算等规划算法,另一方面器上要根据规划结果自主生成运动指令。本文针对自主对地指向需求,提出了一种基于解析星历的火星车自主对地指向方法,并进行了仿真与试验验证,证明了方法的可行性,将应用于我国研制的首个火星车上。
1 对地指向方法概述
对于某个确定时刻,要实现定向天线的对地指向,需解决指向目标确定、转轴运动角度分解、控制指令执行3个关键问题。
1)指向目标确定
火星车对地通信时,无线电信号由定向天线发出,地球上的某个测控站负责接收。地球半径(约6371 km)和地火距离(约0.6~4亿千米)相比很小,所以可将指向目标定为地心。根据天体星历求解火星和地球的相对方位作为指向目标,并通过一系列的坐标系转换,将指向目标转换至火面当地基准坐标系下。需要指出:求解火-地相对方位时需考虑无线电信号的空间传输时间;同时考虑到器载计算机的运算能力,星历计算要尽可能的简洁高效。
2)转轴运动角度分解
根据火星车的姿态将指向目标方位和定向天线波束中心方向统一到同一基准下,然后引入定向天线的安装矩阵、转轴方位等参数,通过矢量变换求解定向天线2个转轴的角度。
3)控制指令执行
由于火-地相对方位是不断变化的,一次指向只能覆盖一段时间。所以定向天线对地指向是一个持续跟踪的过程,在获取转轴运动角度后,还需要确定转轴的运动时刻、运动间隔等参数。
由某个时刻推广至一段时间的对地跟踪指向实施时,需首先根据定向天线波束角、指向误差、指向目标变化速率确定控制周期tcyc,针对每个控制周期,依次完成指向目标确定、转轴运动角度分解、控制指令执行等步骤。需要说明的是,对于t时刻计算得出的转轴角度,若不在有效范围内,则本控制周期机构不运动;若在有效范围内,则进行本控制周期的运动,要求在t-tcyc/2时刻运动到位,使得定向天线指向控制周期中心时刻的目标方位。
2 对地指向详细规划方法
本节针对指向目标确定、转轴运动角度分解、控制指令执行3个关键过程,详细介绍每个过程的计算/规划方法,最后讨论对地跟踪时如何确定控制周期。
2.1 火星车构型及相关约定
为方便后文描述,对火星车及定向天线的相关约定进行说明。
如图1所示,定义火星车控制本体坐标系O B-X BY BZ B:原点O B在火星车结构底板几何中心,O B X B轴指向车头方向,O BZ B轴垂直与底板指向火面,O BY B轴垂直于O B X B轴、O BZ B轴,三轴构成右手直角坐标系。
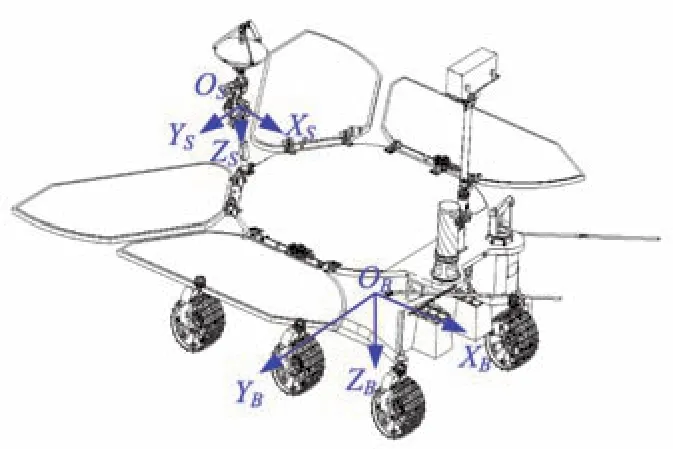
图1 火星车控制本体坐标系定义及定向天线Fig.1 Mars rover control body coordinate system definition and high-gain antenna
定向天线安装在火星车尾部,由双轴机构驱动:转轴A、转轴B,两个转轴互相垂直,A轴转动时带动B轴转动,B轴转动时不影响A轴。定义定向天线双轴零位坐标系O S-X SY SZ S,即定向天线在零位时,O S X S轴指向转轴A,O SY S指向转轴B,O SZ S由右手定则确定;理想安装情况下,双轴零位坐标系三轴指向和火星车控制本体系三轴方向对应平行。
需要指出:定向天线指向前,太阳翼为展平状态,桅杆前倾,以避免车体自身活动机构对定向天线的遮挡。
2.2 指向目标确定
2.2.1 行星位置计算
对于太阳系内的行星,文献[8]给出了J2000.0时刻的轨道根数:轨道半长轴a0、轨道偏心率e0、轨道倾角i0、轨道升交点赤经Ω0、轨道近日点经度˜ω0、轨道平经度L0,以及平均轨道根数的一阶变化率。
对于时刻t(文中以相对器载计算机零时刻的秒数表示,下同),求出其相对J2000.0时刻的时间差值(单位为儒略世纪)为
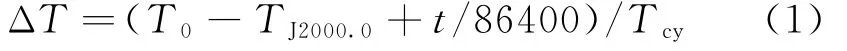
式中:T0为器载计算机零时刻对应的儒略历书日;TJ2000.0为J2000.0时刻对应的儒略历书日;Tcy为一个儒略世纪对应的天数。
据此结合轨道根数的初值以及一阶变化率可求出时刻t的轨道根数a、e、i、Ω、˜ω、L。按照轨道方程可依次求得近日点幅角ω、平近点角M、偏近点角E、真近点角f、轨道轴距r,则在日心黄道坐标系中,天体的位置坐标为
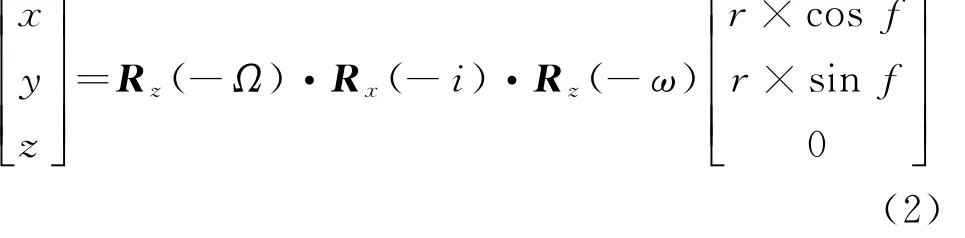
其中:

2.2.2 指向目标方位矢量计算
根据行星位置计算方法,求得t时刻日心黄道坐标系中火星位置坐标,记为rm0(3×1向量,下同);同时,求得t时刻日心黄道坐标系中地球位置矢量,记为re0;两者相减得出火星到地球的相对方位矢量rm0_e0;对rm0_e0取模得出火星到地球的距离Lm0_e0。则信号由火星传至地球的时间简化计算公式为

式中:c为真空中的光速。
如图2所示,定向天线应该指向t+tm0_e0时刻的地球,该方向定义为指向目标。需要指出:不是计算信号出发时刻地球和火星之间的相对方位,也不是计算信号到达时刻地球和火星之间的相对方位,而是计算信号出发时刻火星位置和信号到达时刻地球位置的相对方位。
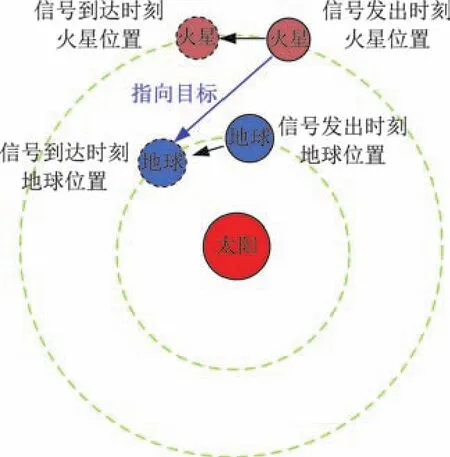
图2 指向目标示意图Fig.2 Pointing target
根据2.2.1节,求得t+tm0_e0时刻日心黄道坐标系中地球位置矢量,记为re;re和rm0作差得出t时刻火星指向t+tm0_e0时刻地球的方位矢量rm_e,对其进行正交化,得到单位方位矢量作为指向目标方位矢量,记为rm_e_N。
2.2.3 火星定向参数计算
如图3所示,文献[9]中给出了国际天球参考架ICRF下,天体北极的方位,其中:P为天体北极;Q为天体赤道升交点;B为天体赤道和本初子午线交点;α0为天体北极在ICRF中的赤经;δ0为天体北极在ICRF中的赤纬;W为0°经线到天体赤道升交点的距离。
对于时刻t,参考式(1)可求出其相对J2000.0时刻的时间差值ΔT1,则有

式中:火星的相关输入参数,如天体赤经参数A、天体赤经参数B、天体赤纬参数C、天体赤纬参数D、天体0°经线距离参数E、天体0°经线距离参数F参见文献[9]。
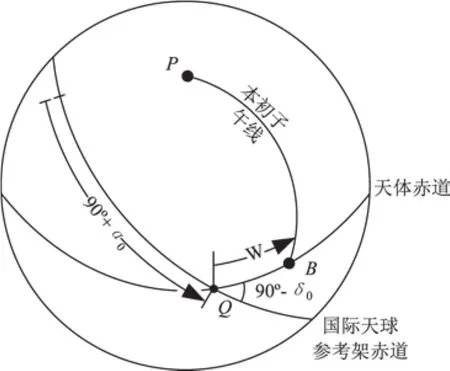
图3 行星定向参考系统Fig.3 Reference system used to define orientation of the planets
给定时刻t,按照式(5)计算出火星的定向参数α0_mars,δ0_mars,Wmars。
2.2.4 指向目标方位矢量坐标系变换
将指向目标方位矢量rm_e_N进行坐标系变换,日心黄道坐标系——国际天文参考坐标系(ICRF)——火星固连坐标系——火星表面天东北坐标系——火星表面北东地坐标系为
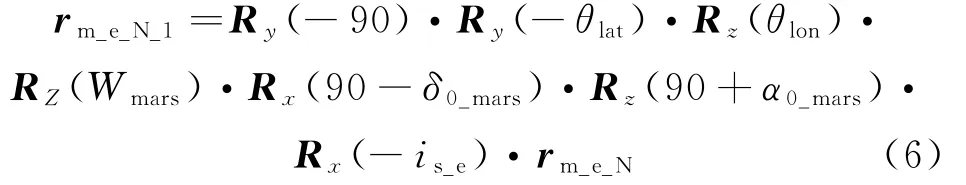
式中:is_e为J2000.0时刻黄赤交角;θlon为火星车所在位置的火面经度;θlat为火星车所在位置的火面纬度。
2.3 转轴运动角度分解
指向目标方位矢量由火星表面北东地坐标系转换至火星车控制本体坐标系为

式中:θyaw为火星车偏航角;θpitch为火星车俯仰角;θroll为火星车滚动角。
指向目标在火星表面北东地坐标系下地球高度角(-90°<he<90°)为

式中:rm_e_N_1(3)表示取rm_e_N_1中的第3个元素,下同。同理可得指向目标在火星车控制本体坐标系下地球高度角(地球相对车体顶面的高度角)heb。
指定北东地坐标系下地球高度角阈值He1和火星车控制本体坐标系下地球高度角阈值He2,根据计算出的高度角判断通信弧段:
若he>He1且heb>He2,表明指向时段在通信弧段内,可以进行后续的指向操作;否则表明指向时段不在通信弧段内,停止指向操作。
若指向时段在通信弧段内,将指向目标由火星车控制本体坐标系转换至定向天线双轴零位坐标系为

式中:Raz为火星车控制本体坐标系至定向天线双轴零位坐标系的旋转矩阵。
定向天线在零位时,其波束中心线(电轴)的方向矢量在定向天线双轴零位坐标系下的表示记为r0;定向天线绕B轴转动θB、绕A轴转动θA后,波束中心线的方向矢量在双轴零位坐标系下的表示为

定向天线绕A轴转动θA、绕B轴转动θB后应该实现对地指向,所以r1=reb1,比较式(10)和reb1有
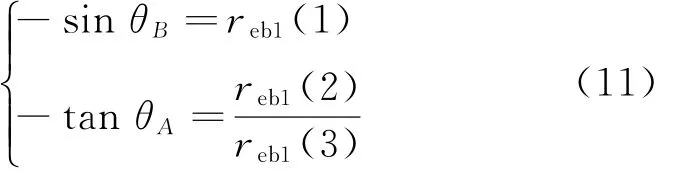
结合实际情况分析得
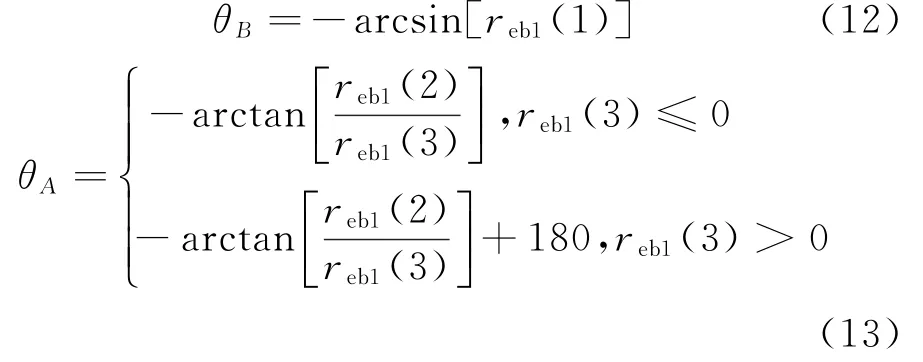
求解完成后,判断θA是否在A轴转动范围内、θB是否在B轴转动范围内:
(1)若2个角度均在规定范围内,则视为有效解;
(2)若有任意一个转角不在规定范围内,则视为无效解。
2.4 控制指令执行
器载计算机的控制指令包括运动速度大小、转动方向、开始转动时刻3类控制参数。
其中A轴、B轴的运动速度大小v A、v B作为输入参数进行指定。
转动方向、开始转动时刻需要计算。按照要求,控制定向天线在t-tcyc/2时刻运动到期望角度。假设2轴可以同时控制,对于每个转轴要求如下。
(1)首先采集当前转角。
(2)计算当前期望转角和当前转角的差值Δθ。
根据Δθ判断转动方向(假定每个转轴执行误差为0.30°),①若 Δθ>0.30°,则正方向转动;②若-0.30°≤Δθ≤0.30°,保 持 不 动;③ 若 Δθ<-0.30°,则负方向转动。
(3)根据Δθ和速度大小计算运动时间tmove(需考虑机构的启停加减速时间)。
(4)开始运动时刻tstart=t-tcyc/2-tmove。
控制参数获取完成后,在tstart时刻发送指令控制转轴运动。
2.5 控制周期确定
对地跟踪时,定向天线需间隔运动,控制周期和定向天线波束角、指向误差、指向目标变化速率相关。
定向天线的波束角记为θbeam,其半波束角为θbeam/2。模拟各种输入偏差,主要包括时刻确定偏差、火面位置偏差、火星车姿态测量偏差、天线安装及变形偏差、天线转轴执行偏差等,依据蒙特卡洛方法进行打靶仿真[10],可以预估定向天线的指向偏差,记为θerr。火-地方位矢量的变化速率记为vem。
若每次瞄准控制周期的中心时刻进行指向,则最大控制周期为
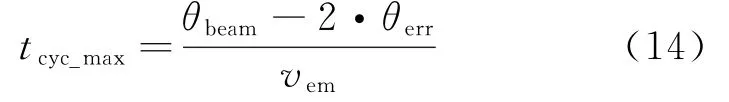
跟踪阶段为保证通信的连续性,控制周期tcyc应小于tcyc_max并留有一定余量。
3 仿真与试验验证
为检验对地指向规划算法的正确性,设计验证系统进行测试验证。鉴于行星位置关系难于模拟,所以验证系统分为如下2个部分。
1)检验星历计算的正确性(涉及2.2节指向目标确定)
使用商用软件(如STK)检验指向目标方向矢量(火-地相对方位矢量)计算的正确性,即将相同输入代入商用软件,然后计算器载计算机输出结果与商用软件输出结果的矢量夹角,以此评价计算的准确性。
2)检验定向天线真实运动结果的正确性(涉及2.3节转轴运动角度分解,2.4节控制指令执行)
在室内试验场搭建验证平台检验定向天线期望波束方向和实际波束方向的一致性。如图4所示,验证平台主要包括多相机摄影测量系统(包括相机,多台相机对控制点和靶标点成像;控制点,布置在场地周围,用于和基准系建立联系;靶标点,布置在待测目标表面,以获得待测目标的位置和姿态;处理软件,实现测量数据的处理和输出控制点、靶标点),模拟火星车(车体及定向天线上粘贴靶标点),校时系统。控制火星车定向天线运动过程中,验证平台可以获得给定时刻的火星车位置、姿态以及定向天线波束方向矢量。通过计算定向天线期望波束方向(同指向目标方向矢量)和定向天线实际波束方向矢量的夹角,以此评价指向的准确性。
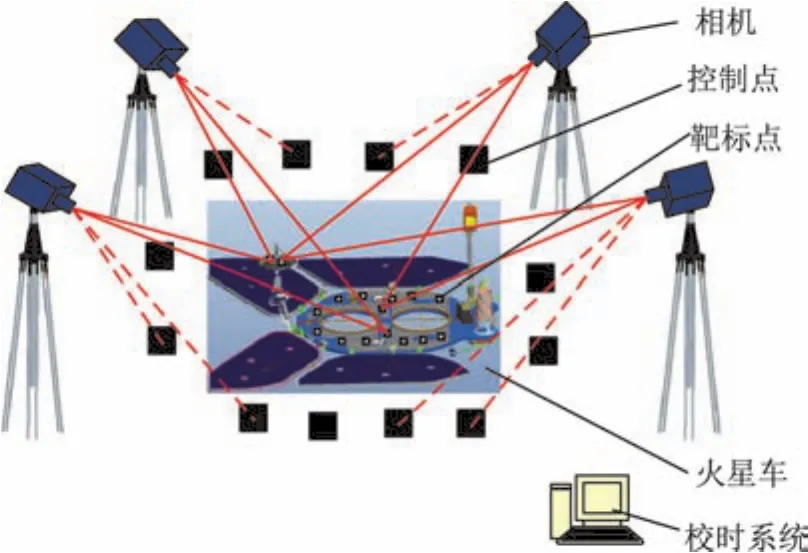
图4 定向天线指向验证平台Fig.4 Verification platform for high-gain antenna pointing
试验数据分析如下。
(1)星历计算结果和商用软件相比最大偏差为0.01°(火星表面北东地坐标系下)。在火星车火面位置(经度、纬度)确定的情况下,此处的偏差主要是星历模型偏差(为提高器载计算机的执行效率,文中使用简化解析星历)。
(2)指向过程中波束中心指向方位矢量的跟踪曲线如图5(a)所示,实测值和期望值的偏差曲线如图5(b)所示,最大偏差为1.18°。此处的偏差包括火星车三轴姿态测量偏差,模拟输入:偏航1.00°(3σ)、俯仰0.50°(3σ)、滚动0.50°(3σ);天线安装及变形偏差,模拟输入:0.10°(3σ);天线转轴执行偏差,模拟输入:0.40°(3σ)、器载计算机时间偏差,模拟输入:1 s。蒙特卡洛分析方法得到的波束中心指向偏差在1.10°(3σ)左右,和试验实测值相当。
(3)除上述偏差外,还需考虑:①定向天线的控制周期,以每2 min调整一次天线为例,2 min地球的方向变化为0.50°,考虑对称性(指向弧段时段中心时刻),地球方向变化角度为0.25°,可以认为是覆盖时长导致的偏差。②火面位置(经度、纬度)测量偏差,一般优于0.20°[11]。
上述偏差之和(0.01°+1.18°+0.25°+0.20°=1.64°)小于定向天线的半波束角(约2.50°),能够保证在轨阶段成功通信。
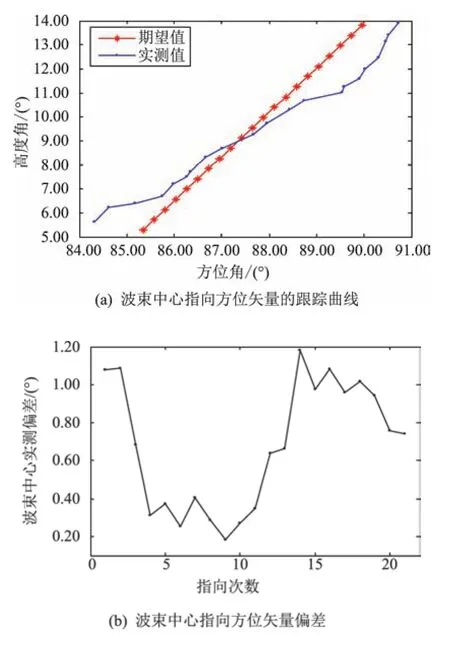
图5 定向天线指向验证试验结果Fig.5 Test result of high-gain antenna pointing
4 结束语
针对火星车的自主对地指向需求,基于解析星历提出了一种可在器上自主运行的对地指向和跟踪方法,解决了数分钟通信时延下火星车定向天线对地球的指向和跟踪问题。根据本文的设计验证系统,模拟在轨输入对算法分段进行验证,试验结果证明了该方法的有效性,满足火星车在轨使用需求。
