应用非线性馈饰算法改进的船舶自动导航控制策略

李 争， 张显库， 马 超

(大连海事大学 航海学院， 辽宁 大连 116026)

船舶航向保持控制算法是大洋航行自动导航的核心算法。对船舶航向保持控制的研究可看作是船舶运动控制领域的一个标准问题，使船舶的航向保持更节能一直是船舶运动控制领域所追求的目标之一，新的控制算法都可将船舶运动数学模型作为被控对象验证控制效果。张显库[1]提出一种基于Lyapunov能量函数构造的非线性控制器，对非线性船舶航向保持控制系统具有更好的控制性能和鲁棒性能。SUN等[2]提出一种新的基于Lyapunov的自适应逻辑切换规则，寻求船舶航向系统的正确控制方向，理论分析和仿真结果证明所开发控制方法的有效性。ZHANG等[3-4]提出非线性反馈控制的方法并将其应用于船舶运动控制，并采用正弦函数的非线性反馈算法对航向保持自动舵算法进行改进，达到节能的目的。MOBAYEN等[5]提出一种复合非线性反馈控制技术的设计方法，用于具有时变时滞、Lipschitz非线性函数和参数不确定性的主/从非线性系统的同步。张显库等[6]采用双极性S函数修饰技术结合线性鲁棒控制算法构成一种控制算法的控制能量。马超等[7]设计基于指数非线性反馈的航向保持控制算法，并验证其节能的特点。张显库[8]采用正弦函数驱动自动舵控制算法，应用正弦函数的非线性反馈技术，对控制器的输入进行处理，并于2017年提出一种基于Lyapunov候选函数的改进成简洁Backstepping控制器，引入误差非线性函数代替反馈环路中的误差本身。[9]ZHANG等[10]将双极性S函数非线性反馈应用于比例积分和微分(Proportion Integral Differential, PID)控制器，对船舶的日本船舶操纵数学小组模型进行靠泊仿真试验，证明该方法具有鲁棒性，安全节能的特点。ZHANG等[11]设计基于正切函数非线性反馈的船舶自动舵航向保持控制器，并验证其节能的特性。WU等[12]设计基于双极性S函数非线性反馈控制算法的控制器，并进行理论分析，达到船舶运动控制和节能的目的。CHEN等[13]将非线性反馈技术应用于自适应模糊控制，并对油船进行仿真试验证明非线性反馈技术的快速稳定和航向偏差较小的特点。

1) 线性反馈的任务是设计一个控制律u=f(e)e，其中：f(e)是传统意义上的控制律，是反馈误差e的线性函数或非线性函数；而误差e不做任何处理，直接反馈到控制器的输入端。

2) 非线性反馈设计的控制律是u=f(e)g(e)，其中：g(e)为关于反馈误差e的非线性函数；非线性修饰设计的控制律为h(u)=f(e)e，h(u)为控制器输出u的非线性函数。非线性反馈和非线性修饰技术经过仿真验证都能实现节能的控制效果，本文在此基础上设计非线性馈饰控制律h(u)=f(e)g(e)，即同时对反馈误差和控制器的输出进行非线性处理，并通过仿真试验来验证控制律的有效性。

1 非线性船舶模型

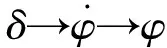
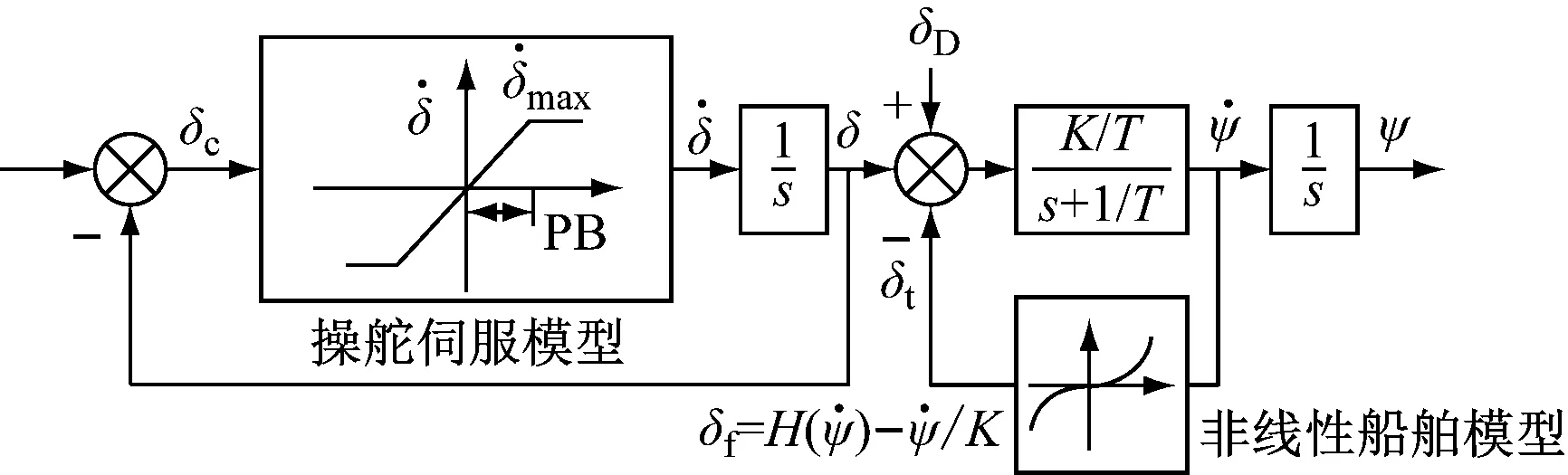
图1 非线性的船舶运动数学模型

以大连海事大学新一代教学实习船“育鹏”轮为对象建立船舶运动数学模型，“育鹏”轮在2016年交付并使用，并于2017年进行首航，其各项试验数据较为完备，对于验证船舶模型和实际船舶情况的符合度具有重要意义。船舶模型采用上述Nomoto模型，并且带有非线性反馈补偿项。对于建立船舶运动Nomoto模型所需要的船舶参数见表1。

表1 “育鹏”轮船舶参数

根据航海实践，驾驶台下达舵令后，船舶应舵存在延迟，并且舵机的转舵速率具有限制，为更加真实地模拟实际船舶情况，在仿真中考虑舵机的上述特性，并加入舵机伺服系统，舵机伺服系统是由比较器、功放、变量泵、液压舵机和舵机反馈装置组成的。在此系统中舵角δ的范围是[-35°,35°]，转舵速率最大为5(°)/s。非线性船舶模型系统结构如图1所示。

由舵角δ和艏向角ψ分别作为被控对象输入与输出，可得被控对象的Nomoto传递函数模型为

(1)

非线性反馈补偿项为

(2)

式(1)和式(2)中：参数K和T均可根据表1给出的数据通过代入流体动力导数估算，修正公式并应用Norrbin模型进行编程计算得到[15]；而参数α和β则可通过系统辨识得出[6]；s为拉普拉斯算子。

模型建立完成不能够直接用来进行试验，必须要与船舶的实测数据对比进行模型验证，只有模型的精度达到要求才能够被用来进行船舶的仿真试验。对于验证模型精度，参考文献[6]有符合度公式为

符合度=

(3)

为验证所建立的响应型非线性船舶模型和真实船舶的符合度，采用SIMULINK对模型进行右满舵旋回试验，并将得到的仿真曲线和实船试验曲线进行对比结果(见图2)，经计算可知该仿真的回转圈与实船试验回转圈拟合度为89.52%，就模型本身的精确度而言，仿真结果令人满意。

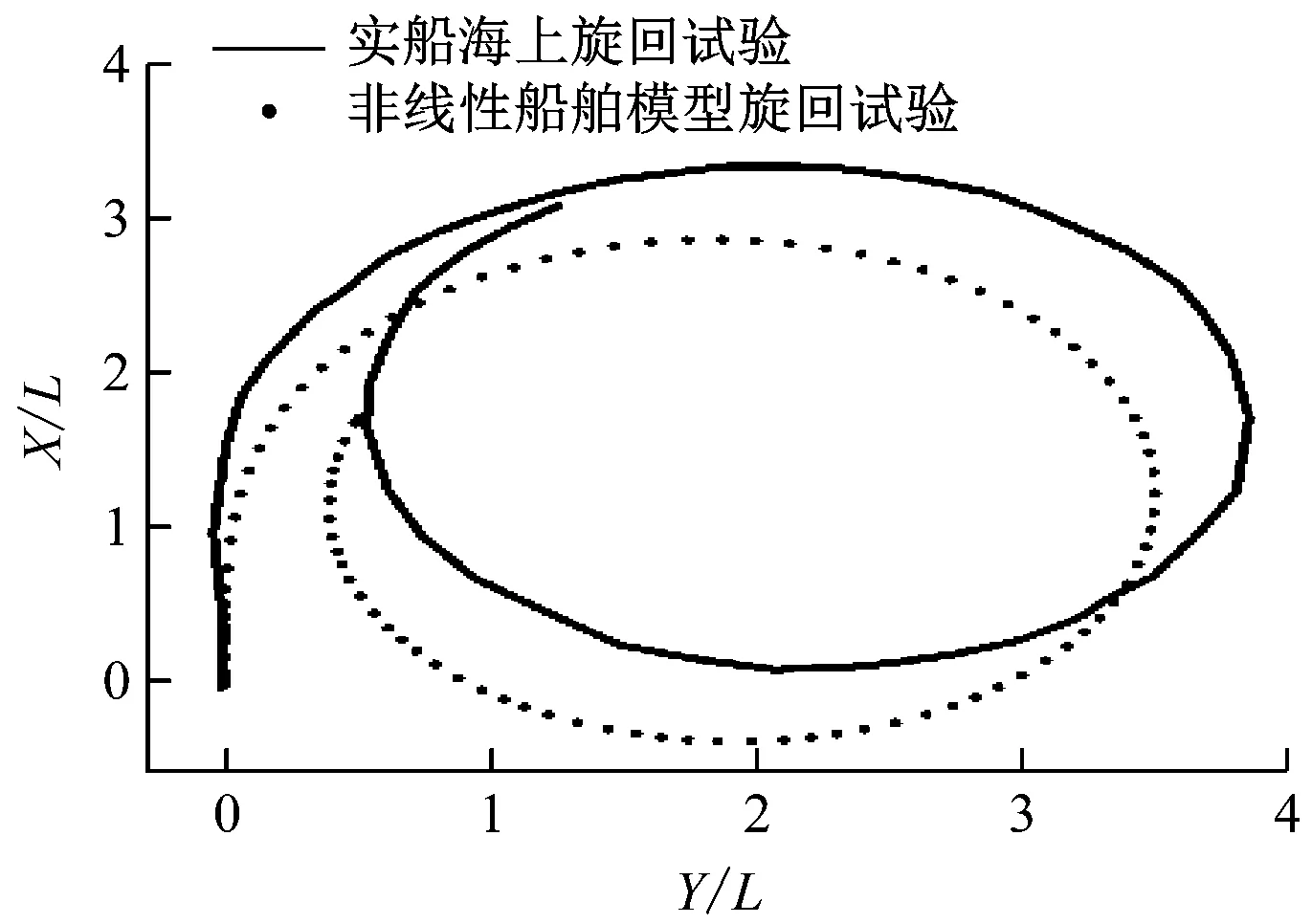
图2 右满舵旋回圈对比图

2 非线性馈饰技术改进PID控制器设计

2.1 PID控制器设计

针对上述非线性Nomoto 模型，采用一阶闭环增益成形算法，即设闭环系统具有1/T1的带宽频率(或交接频率)，关门斜率(或高频渐近线斜率)取-20 dB/dec 时，设计PID控制器，将补灵敏度函数T的奇异值曲线近似表示为最大奇异值为1的一阶惯性系统的频谱曲线，具体表示为

(4)

可得

(5)

式(5)中：K为控制器；G为被控对象；s为拉普拉斯算子。

将式(1)代入式(5)可得式(6)标准形式的PID控制器，其中ε为一个小数，用来消除控制系统静差。

(6)

对于有着较大时间常数的船舶，控制器的调节时间过长。通过研究发现在控制律的比例部分加上一个正常数ρ=2，船舶航向保持的效果有显著提升。最终，实际的控制器见式(7)，PID的初始值就是根据式(7)来确定的。

(7)

2.2 非线性馈饰技术改进PID控制器

非线性反馈技术是对控制器的输入进行非线性处理(见图3)；而非线性修饰技术是从另一个角度出发，用非线性函数对控制器的输出进行处理(见图4)。

图3 非线性反馈系统框图

图4 非线性修饰系统框图

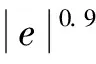
图5 非线性馈饰系统框图

3 仿真验证与结果分析

船舶在实际的航行中所受到的风浪干扰在仿真中也是需要考虑的。船舶实际所受到的风干扰可分为平均风干扰和脉动风干扰，对于平均风干扰的影响可采用等效压舵角在仿真中予以表示；而脉动风干扰则采用白噪声来代替。海浪干扰采用式(8)来模拟表示。

y(s)=h(s)w(s)

(8)

式(8)中：w(s)为零均值高斯白噪声；h(s)二阶海浪传递函数。本文中采用的h(s)为

(9)

最终得到系统仿真框图见图6。

通过对系统进行仿真试验，设系统输入为80，即设定船舶航向从正北转为080°，标准PID控制器和非线性馈饰作用下PID控制器(简称馈饰PID)的仿真航向对比见图7。由图7可知：PID控制器作用下的控制效果与非线性馈饰PID控制器近似，两者最终达到稳定的航向所需时间基本相同，并且都较为迅速，约为120 s。2种控制技术下舵角的变化幅度见图8。由图8可知：使用非线性馈饰技术能够大幅度地减小航向保持控制过程中的操舵幅度，并且标准PID和馈饰PID使用的最大舵角均为35°；通过计算可知标准PID的平均舵角是9.8°，非线性馈饰PID的平均舵角为4.92°，平均舵角减少4.88°，降幅约为50%。以上的仿真试验与结果分析表明非线性馈饰技术要比标准PID更节能。几种不同的非线性技术作用下的舵角对比(由于航向仿真结果差别不是很明显，所以其仿真曲线这里不再给出)见图9，其中：幂函数反馈控制器的最大舵角为35°，平均舵角是7.97°；双极性S函数非线性修饰控制器的最大舵角是35°，平均舵角为6.51°；指数函数非线性反馈控制器最大舵角为35°，平均舵角为6.12°；幂函数非线性馈饰控制器最大舵角为35°，平均舵角为4.92°。在航海中使用舵机驱动舵叶改变舵角，因此较小的舵角意味着较小的能量消耗，由此可知上述4种非线性方法中幂函数非线性馈饰最为节能，见表2(其中设PID控制能量消耗为单位1)。

图6 系统仿真框图

图7 标准PID与馈饰PID航向仿真对比图

a) 标准PID舵角仿真图b) 馈饰PID舵角仿真图

图8 标准PID与馈饰PID舵角仿真对比图

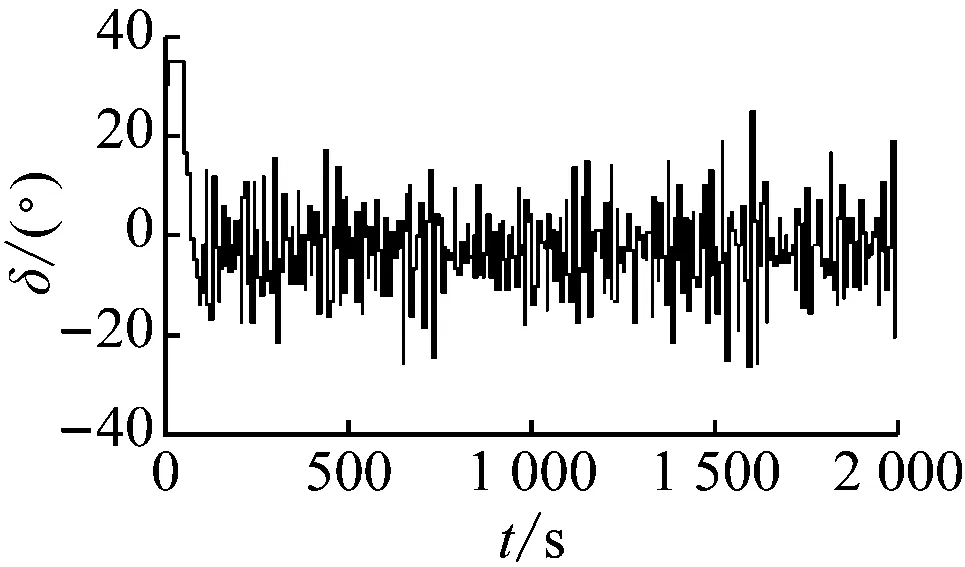
a) 非线性反馈——幂函数

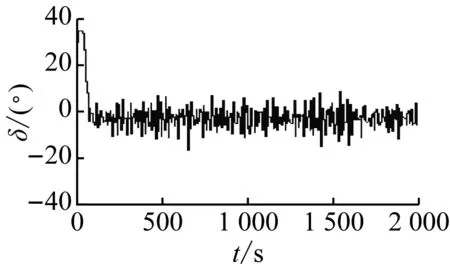
b) 非线性馈饰——幂函数

c) 非线性反馈——指数函数

d) 非线性修饰——双极性S函数

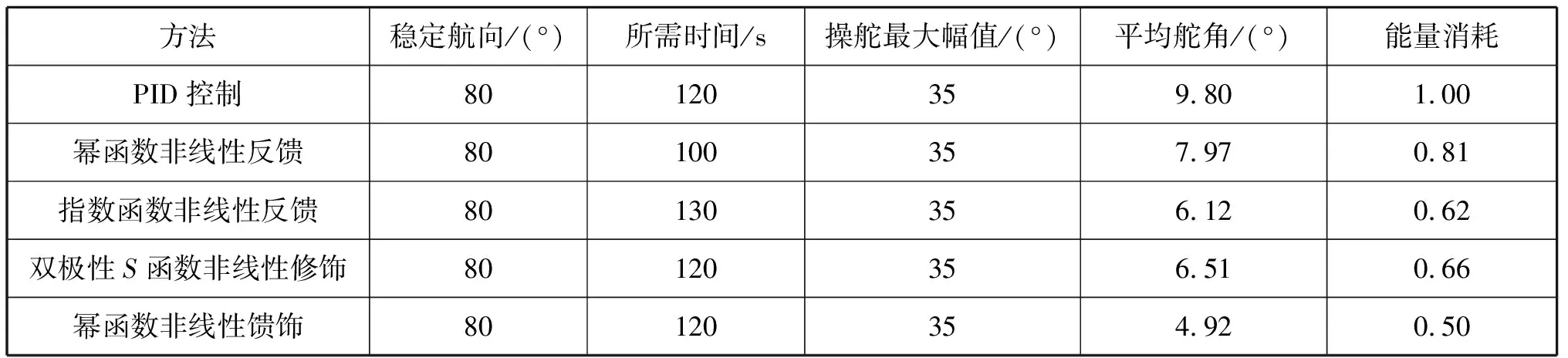
图9 不同非线性技术作用下的仿真舵角图

4 结束语

应用非线性馈饰技术对PID控制器的输入和输出进行非线性处理，设计新的船舶航向保持控制算法，加入贴近航海实践的操舵频率限制，并通过对“育鹏”轮进行仿真试验从而验证新算法的有效性。仿真结果表明:非线性馈饰改进的船舶航向保持控制算法能够很好地实现航向保持控制的目标，航向保持过程中的平均舵角较标准PID控制器下降50%，并且与在其他非线性技术的比较中体现出非线性馈饰算法的更加节能的特点，应用于实际船舶能够节省船舶在航行和实际运营中的能量消耗，对船舶航向保持控制研究的后续开展具有重要意义。