不同楼梯布局条件下行人疏散效果仿真研究*

2019-05-09李若菲赵永翔卢团团刘旭光

中国安全生产科学技术 2019年4期

李若菲，赵永翔，卢团团，刘旭光

(福州大学经济与管理系，福建福州 350116)

0 引言

近年来，建筑火灾造成的人员伤亡事件屡有发生，尤其对于人员密集、火灾荷载大的场所，一旦发生火灾极易造成重大人员伤亡和财产损失，甚至造成恶劣的社会影响[1]。楼梯是各种建筑物中的主要疏散环节，特别是一些大型的人群聚集场所，如火车站、地铁站、商业广场、教学楼等。在紧急事件发生时(如停电、火灾、地震等)，楼梯也是主要的逃生通道。而楼梯疏散在疏散速度、步幅宽度、人员间相互影响等方面都不同于平面上的疏散[2]。因此，针对楼梯区域人员疏散特征进行研究具有重要的现实意义。

对于人员疏散问题，常使用的行人模型主要是社会力模型[3]、元胞自动机模型[4]及格子气模型[5]等。其中，Helbing等[3]提出的社会力模型是研究行人流领域的空间连续模型，以分析行人间的物理力和心理作用力为主，能够复现一些自组织现象，如成拱现象等。目前许多学者使用该模型对楼梯上的行人流进行仿真研究。Seyfried等[6]用改进的社会力模型研究楼梯区域行人运动特性，并分析楼梯尺寸、台阶的限制以及速度的影响等；Wu等[7]结合行人自身重力因素改进了社会力模型，来研究狭窄的楼梯空间中行人的运动特性；李娟等[8]基于传统社会力模型，引入重力分力和边界吸引力来描述行人在阶梯路段的运动特征。但这些研究大多为二维空间的模拟，忽略了竖直方向上的运动。

现实生活中，不同布局的行人交通设施有不同的通行能力，而不合理的设计会导致交通拥堵，影响行人的正常行走，合理的设计则能提高交通设施的通行能力，缓解行人拥挤并节约资源。Mona Afifi等[9]研究了对老年人安全友好的楼梯布局，提出基于证据的评估方法来评估楼梯元素，并结合数学模型与设计评估树的场景评级系统预测不同类型的建筑楼梯设计的跌落风险程度；丁元春等[10]和郭晓明等[11]利用Pathfinder仿真平台研究了高层建筑中2种楼梯布局下的行人疏散效果，并对比分析了宏观上的疏散指标，即总疏散时间和平均疏散速度。但目前鲜有关于不同楼梯布局条件下行人疏散行为的宏微观特征的对比分析。

本文拟从三维视角，用改进的社会力模型对4种常见楼梯布局下(即单跑有平台梯形，单跑无平台梯形，双跑梯形及双分梯形)的行人疏散特征进行宏微观对比分析。并按以下研究思路开展工作：首先对传统社会力模型进行改进；然后对4种常见的楼梯布局进行模拟分析；最后，通过分析总疏散时间、平均疏散速度及速度及密度分布图来探讨这4种常见楼梯布局的疏散效果，以期为建筑中的楼梯布局选择、设计及规划提供一定的参考依据。

1 三维SFM构建

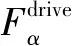
(1)

(2)

其中：行人α的空间位置sα(t)的变化可由vα(t)=dsα/dt来计算。

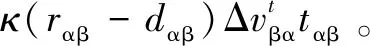
因此，行人α，β的作用力可以根据方程定义为：

(3)

当行人之间并未接触时，函数g(x)=0，否则为复数x。

类似的，与墙壁w的作用力也可以通过方程得到：

(4)

式中：dαw表示到墙壁w的距离;nαw表示垂直与墙壁的单位向量;tαw表示正切于墙壁的方向。

行人上下楼梯的过程是1个典型的三维运动，不仅包括水平(x-y平面)方向上的运动，还包括垂直(z轴)方向上的运动。因此，在传统的二维社会力模型的基础上，考虑垂直方向上的运动，构建三维(x-y-z)社会力模型。

三维楼梯运动速度分解示意如图1所示。行人的实际速度vα可以被分解为vx，vy以及vz，即

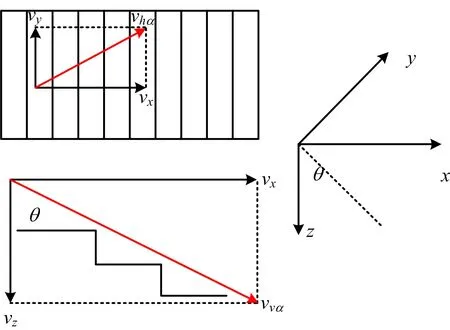
图1 楼梯运动速度分解示意Fig.1 Diagram of stair movement speed decomposition

(5)

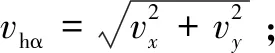
根据实验观察，行人在楼梯上运动时，竖直方向上的速度vz依赖于水平方向上的速度vx，即

vz=vxtanθ

(6)

式中：θ指楼梯的坡度。当行人在台阶上行走时，θ为楼梯实际坡度值；当行人在中间平台等平坦区域运动时，θ被设为0。

2 4种常见梯形下行人疏散仿真及分析

2.1 4种常见梯形示意图

根据调查发现，建筑场所中常使用的楼梯类型为单跑有平台、单跑无平台、双分及双跑。这4种梯形的定义见文献[12]，即单跑无平台：上下楼层只有1个楼梯梯段由上而下；单跑有平台：在无平台基础中间设有1个平台；双跑：上、下楼层之间设有2个楼梯梯段，梯段在平面位置上互相平行，梯段之间通过楼梯平台连接；双分：包含3个梯段，第1梯段位于楼梯间中部位置，第2和第3梯段则分别位于第1梯段两侧，第2，3梯段的宽度均为第1梯段的1/2，中间通过楼梯平台连接(图2)。

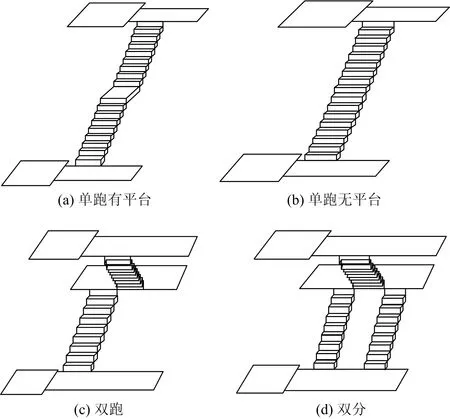
图2 4种梯形示意Fig.2 Schematic view on the staircase configurations

2.2 仿真楼梯参数设置

对这4种楼梯布局的行人疏散过程分别进行模拟。建筑仿真模型的区别仅在于楼梯梯形不同，即假定在限定空间中，4种楼梯都是两层高，单个楼梯段竖直高度为2.72 m，每段楼梯含16个台阶(单跑无平台楼梯一共32个台阶)，每个台阶高0.17 m、深0.33 m，坡度为27.3°。笔者通过实际测量学校教学区楼梯尺寸来设置参数，且符合《民用建筑设计通则》和《建筑楼梯模数协调标准》。台阶参数和4种梯形平面示意如图3所示(箭头和序号表示行人运动方向)。

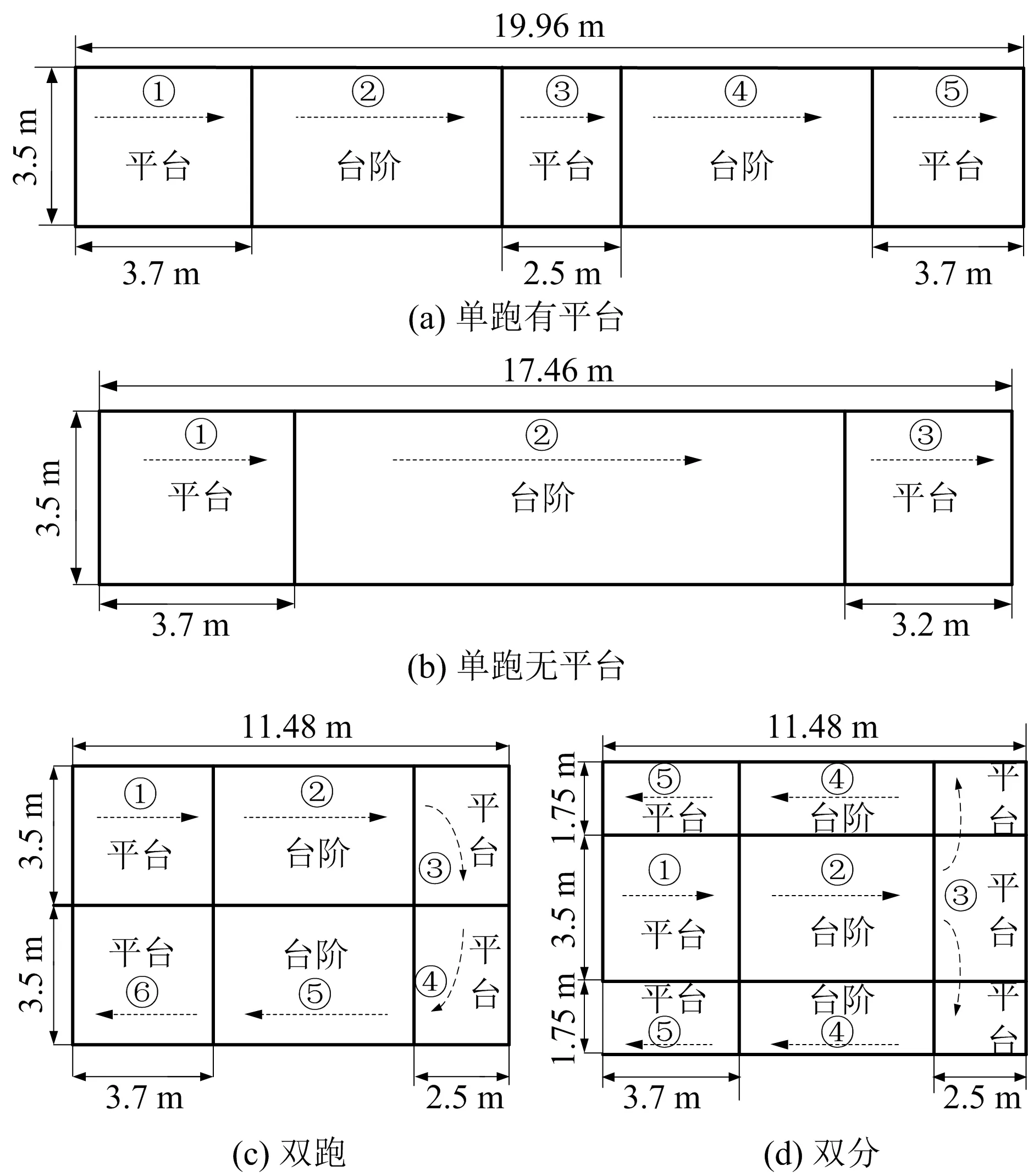
图3 4种梯形平面示意Fig.3 Schematic diagram on the staircase configurations

2.3 仿真结果分析

用改进的三维社会力模型对4种楼梯类型进行模拟，得到其疏散场景图及运动轨迹(图4)。

图4 疏散场景图及其运动轨迹Fig.4 Evacuation scene map and motion track

2.3.1 4种梯形总疏散时间

为了分析不同梯形中人员密度对疏散效率的影响，将初始人群密度划分成低、中、高3个水平，即低于0.3人/m2为低密度人群，0.3～1.4人/m2为中密度人群，大于1.4人/m2为高密度人群[13]。根据楼梯面积，将初始人数分别设为10，20，60，80，120及130人，通过上述的三维社会力模型进行仿真，模拟结果如图5所示。

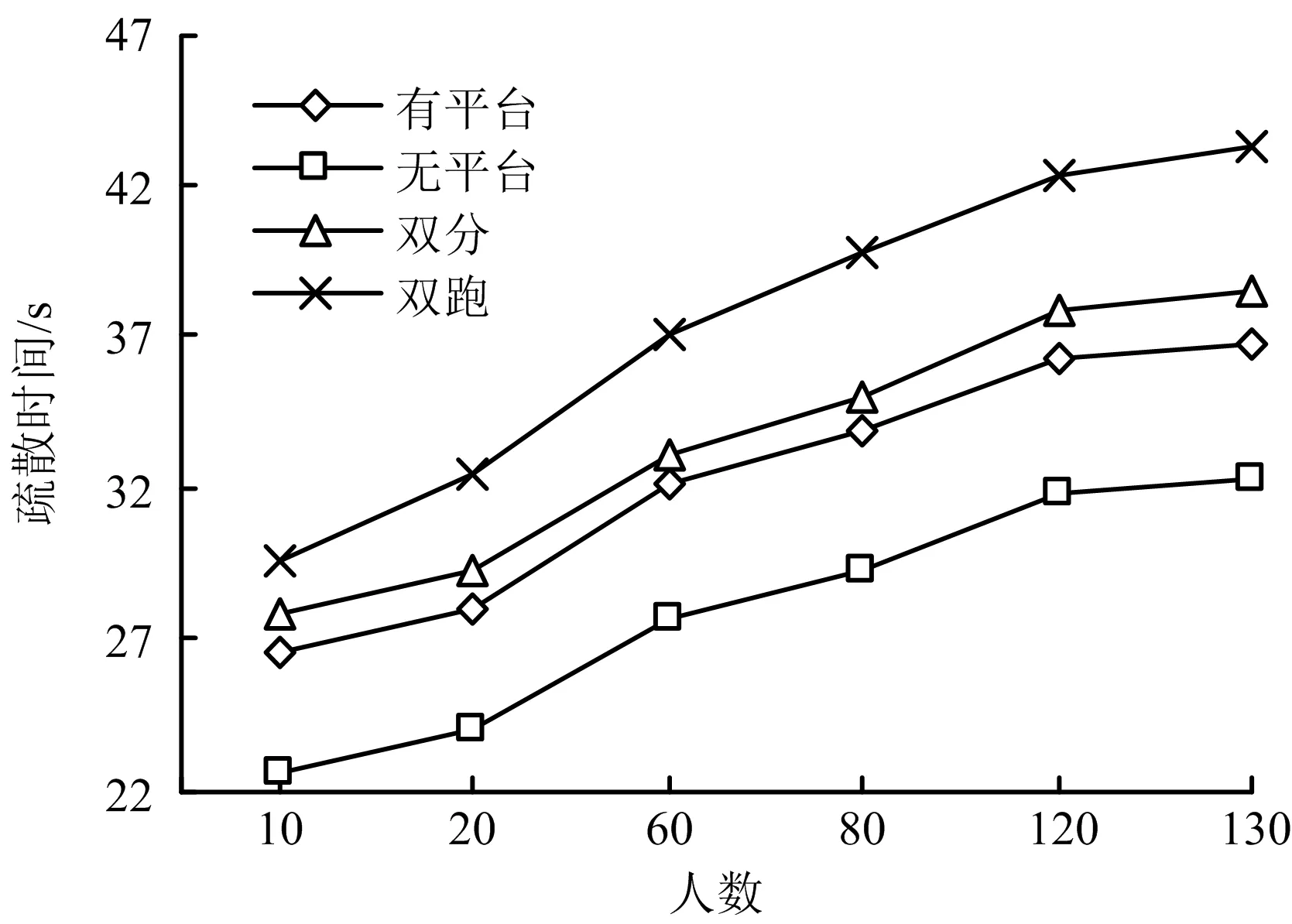
图5 不同人群密度下4种梯形的行人总疏散时间Fig.5 The total evacuation time of four kinds of stairs under different population density

从图5中可看出，在限定空间中，随着总疏散人数的增加，4种楼梯类型的疏散时间线性增加。在3种初始人群密度下，单跑无平台梯形疏散时间最短，双跑梯形疏散时间最长。如在初始人数为10人时，单跑无平台疏散时间为22.645 s，单跑有平台为26.590 s，双分为27.808 s，双跑为29.537 s；最大疏散时间差为7 s左右，最小疏散时间差为1 s左右。在初始人数为60人时，单跑无平台疏散时间27.721 s，单跑有平台为32.183 s，双分为33.124 s，双跑为37.094 s；最大疏散时间差为9 s左右，最小疏散时间为1 s左右。在初始人数为130人时，单跑无平台疏散时间为32.303 s，单跑有平台为36.788 s，双分为38.410 s，双跑为43.137 s；最大疏散时间差为11 s左右，最小疏散时间差为2 s左右。即单跑有、无平台梯形布局在疏散时间上快于双分、双跑梯形布局；单跑无平台梯形快于单跑有平台梯形；双分梯形快于双跑梯形。这表明1个楼梯段疏散时间最短，而1个楼梯段中平台的设置会延迟疏散；3个楼梯段的疏散时间比2个楼梯段短。

2.3.2 4种梯形平均疏散速度

为进一步分析不同梯形的疏散能力，用人员疏散速度指标来反映疏散能力的快慢，即单位时间内完成疏散的人员数量。先从宏观角度来看4种布局楼梯在不同人群密度情形下的平均疏散速度，如图6所示。

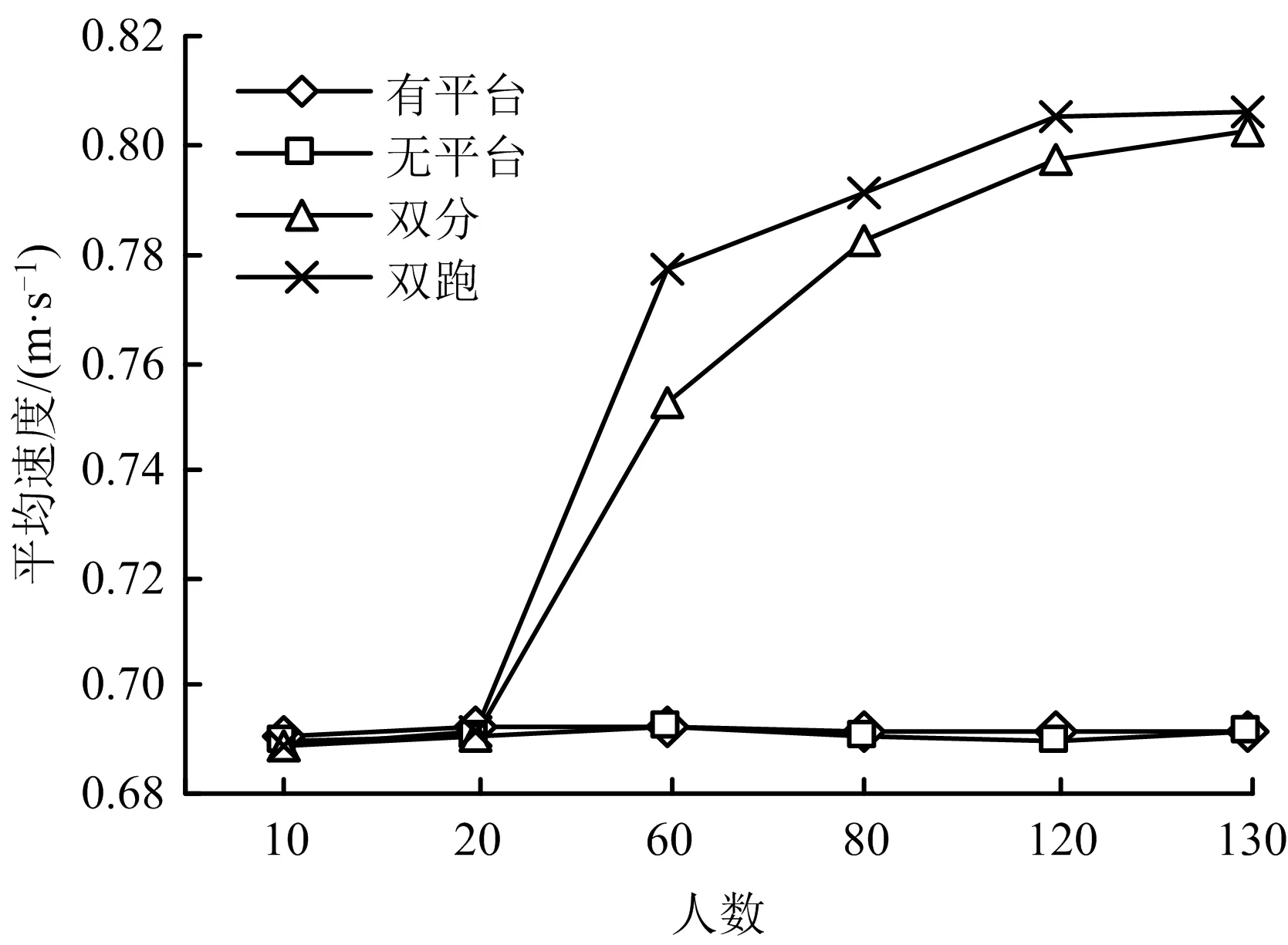
图6 不同人群密度下4种梯形的行人平均疏散速度Fig.6 The average evacuation velocity of four kinds of stairs under different population density

首先，从图6中可以看出，在初始人数为低密度情形下，在限定空间中4种楼梯布局的疏散速度接近，比如当初始人数为20人时，单跑有平台疏散速度为0.691 9 m/s，单跑无平台为0.690 8 m/s，双分为0.690 1 m/s，双跑为0.691 8 m/s。速度都接近渴望速度0.7 m/s，这表明初始人数为低密度情形下，在限定空间内考虑有无平台梯形会有利于人员更快地疏散。

而在初始人数为中、高密度情形下，单跑有、无平台的疏散时间短，但疏散速度小。从理论上讲，在限定空间内，由于结构布局不同，人员在单跑有、无平台楼梯上的疏散总路程比双分、双跑长，速度应该也大于双分、双跑梯形。而从实际模拟结果上看二者的速度慢于双分、双跑，这表明相较于2个和3个楼梯段，1个楼梯段人员活动空间范围小，会使人员相互碰撞而造成拥堵，最终导致人员在楼梯上的疏散速度变小。

比如当初始人数为60人时，双跑平均疏散速度为0.777 m/s，双分为0.753 m/s，单跑无平台为0.692 2 m/s,单跑有平台为0.692 5 m/s。当初始人数为120人时，双跑平均疏散速度为0.806 m/s，双分为0.797 9 m/s，单跑无平台为0.690 m/s，单跑有平台为0.691 m/s。值得注意的是，在中、高密度情形下，双分、双跑梯形平均疏散速度大于渴望速度0.7 m/s，说明此时人员之间并没有发生拥堵，反而提高了人员疏散速度。但速度的增加并没有带来更短的疏散时间。这表明，虽然单跑有、无平台疏散时间快于双分、双跑梯形，但其不具有分流特点，易发生拥堵，因此其事故风险发生率也比双分、双跑梯形高。

其次，从图6中可以看到，在3种密度情形下，单跑有、无平台速度十分接近，但单跑无平台疏散时间明显快于单跑有平台，最大时间差为5 s，最小时间差约为3.5 s。说明平台的设置会延迟疏散时间，单跑无平台比单跑有平台更有利于人员的快速疏散。

最后，虽然在3种初始人群密度情形下，双分疏散时间明显快于双跑。但在低密度情况下，双分和双跑梯形疏散速度相差不大。比如当初始人数为20人时，双分疏散速度为0.690 m/s，双跑疏散速度为0.692 m/s；而中、高密度情况下，双跑速度稍大于双分速度。比如当初始人数为60人时，双跑疏散速度为0.777 m/s，双分疏散速度为0.752 m/s。这是因为双跑比双分少1个楼梯段，人员拥挤在一起，但这种拥挤程度并不造成拥堵，反而提高了人员的速度。但其速度增加并没有带来比双分更短的疏散时间。当人群密度为高密度时，双分、双跑速度趋于接近。比如，当初始人数为130人，双分疏散速度为0.803 m/s，双跑疏散速度为0.807 m/s。综上可知，双分梯形比双跑梯形多了1个楼梯段，分流优势更能体现在疏散时间上。因此双分比双跑更有利于人员快速疏散，且发生事故风险率也较低。

2.3.3 4种梯形密度和速度分布图

为了探讨这4种梯形的内在物理机制，通过Voronoi方法得到其密度、速度分布图。笔者选取初始密度为60，130人的密度和速度分布图进行探讨。图7与图 8分别表示单跑有平台、单跑无平台、双跑、双分4种梯形在中、高密度情形下的密度分布图。图9与图10分别表示有平台、无平台、双跑、双分4种梯形在中、高密度情形下的速度分布图。

图7 60人的密度分布Fig.7 The density profiles for 60 people

图8 130人的密度分布Fig.8 The density profiles for 130 people

图9 60人的速度分布Fig.9 The velocity profiles for the stair for 60 people

图10 130人的速度分布Fig.10 The velocity profiles for 130 people

从图7中可以看到，4种梯形在人员疏散过程中容易造成不同位置的聚集拥堵，即发生事故风险的位置不同。如单跑有平台和单跑无平台2种梯形在楼梯开始疏散的上端和结束疏散的下端，其位置的密度值达到最大值(2.5人/m2以上)，而双分梯形和双跑梯形在上端楼梯和平台连接处，即拐角处易造成人员拥堵，其密度值也达到2.5人/m2以上。值得注意的是，在相同人员密度情形下，双分梯形由于分流特点，其易发生拥堵的部分比双跑梯形小，这说明双分梯形发生事故风险的概率低于双跑梯形。如在人员密度为130人时，可看到双跑梯形易拥堵的位置面积约是双分梯形的2倍。

根据泰森多边形计算方法，单跑有平台梯形在2种初始密度情形下，其最大密度值为5.51和6.45人/m2；单跑无平台梯形的最大密度值为4.89和6.71人/m2；双分梯形为3.06和5.35人/m2；双跑梯形为4.55和6.13人/m2。

图9、图10表示4种梯形在2种密度情形下人员疏散的微观速度分布状态。从图中可看到其速度值变化从中密度人群到高密度人群与图6的趋势相同。如图9(a)中单跑有平台梯形在初始人数为60人时，其最大速度值为0.81 m/s，平均疏散速度为0.692 5 m/s；图10(a)中初始人数为130人时，其最大速度值为0.87 m/s，平均速度值0.691 8 m/s。图9(b)、10(b)中的单跑无平台梯形在2种密度下的楼梯区域最大速度分别为0.82和0.99 m/s，其平均疏散速度分别为0.692 2和0.691 9 m/s。即单跑有、无平台速度分布相差不大。而双分梯形和双跑梯形的速度分布在2种密度情形下有明显的颜色变化过程，即从中密度到高密度情形下，楼梯区域的灰色部分渐变到黑色部分。图9(d)、10(d)中的双分梯形楼梯区域最大速度分别为0.76和0.83 m/s，其平均疏散速度分别为0.752 7和0.802 8 m/s。图9(c)、10(c)的双跑梯形楼梯区域最大速度分别为0.82和0.83 m/s，其平均疏散速度分别为0.776 9和0.806 5 m/s。