弹性安装条件下机械设备自由振速测量方法*

王 真, 赵志高

(1.武汉纺织大学机械工程与自动化学院 武汉, 430200) (2.武汉纺织大学数字化纺织装备湖北省重点实验室 武汉,430200) (3.武汉第二船舶设计研究所 武汉,430205)

引 言

设备振动源特性用于表征机械设备振动的固有特性。描述设备振动源特性的关键问题是源特性表征量的选取及其获取方法。Breeuwer等[1]提出采用自由振速 (free velocity) 描述设备的振动源特性，自由振速[2]是指设备在自由悬挂条件下测得的设备机脚的振动速度，自由振速不受测量环境的影响，能够表征设备振动的固有特性。目前，自由振速作为设备源特性的表征量已经得到了认可，是描述设备振源特性的优选参数[3-11]。

但是，自由振速的获取存在一定困难，主要原因是自由振速的直接测量条件苛刻，在工程中难以实施。Plunt[2]指出，自由振速的自由悬挂条件可以通过在设备安装软弹簧来近似满足。原春晖[9]从工程实际出发，针对自由振速测量过程中的有效频率范围、设备安装要求、测量环境和背景噪声、隔振器选型以及测点布置等问题进行了详细的分析。朱正道等[10]归纳了测量设备自由振速的安装条件，其实验数据表明：若隔振器上下端的振级差达20 dB，可将测得的设备振速作为自由振速。严斌等[12]的研究表明，当机脚阻抗与隔振器阻抗失配程度达10倍以上时，测得的机脚振速可作为自由振速。

上述研究表明,当隔振系统满足一定条件时，可将弹性安装条件下的设备机脚振速近似作为自由振速，但是此结论仅基于实验数据，而并未进行理论证明及其误差分析。鉴于此，笔者开展了弹性安装下设备自由振速测量方法的理论研究和实验验证。首先，利用阻抗综合分析法建立动力学方程；然后，利用有效点导纳分析了隔振系统对自由振速的影响规律，获得了自由振速与机脚振速之间的关系，进而提出了自由振速的测量方法；最后，对该测量方法进行了理论误差分析，用有限元模拟和实验验证了该方法的正确性。

1 理论分析

1.1 基于阻抗分析的多点耦合隔振系统建模

如图1所示，对由设备、弹性支撑以及基座所构成的单自由隔振系统，可采用阻抗综合分析方法，建立系统多点多激励的动力学模型。

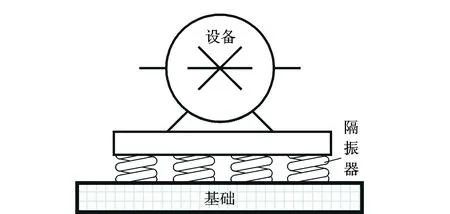
图1 单层隔振系统简图Fig.1 Diagram of single raft system

设设备机脚的自由振速向量为V0，安装隔振器后，设备机脚的振动速度向量为Vu，基座安装点处的振动速度向量为Vb,Hu为隔振器与设备连接点所构成的导纳矩阵，Hb为隔振器与基座连接点所构成的导纳矩阵,Fu和Fb分别为隔振器作用在设备和作用在基座上的激励力向量。

根据导纳函数的定义，对设备建立以下模型[13]

Vu=V0-HuFu

(1)

其中：Hu为设备机脚所构成的导纳矩阵。

其表达式为

(2)

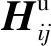
同理，对于基座有

Vb=HbFb

(3)

对隔振器，根据四端参数模型可得

Fu=Z11Vu+Z12Vb-Fb=Z21Vu+Z22Vb

(4)

其中：Z11，Z12，Z21和Z22分别为隔振器阻抗矩阵。

由式(1)～(4)可得单层隔振系统的动力学方程为

(5)

由式(5)可知，多点耦合的单层隔振系统的变量互相耦合，设备在不同安装点之间的振动速度也是耦合的，无法直接分析隔振系统对自由振速的影响。因此，本研究引入有效点导纳的概念，将多输入多输出耦合系统转化为多个单输入输出系统，在此基础上分析隔振系统对设备自由振速的影响。

1.2 基于有效点导纳的自由振速估算

有效点导纳是指单个接触点处、单方向上实际振动速度与所有接触点、所有激励分量在该点产生的单方向实际力的比值。因此，在多点激励下，考虑所有点不同自由度对测量点的影响时，有效点导纳定义[9;14]为

(6)

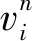
对式(6)进行变形，得到如下有效点导纳的表达形式[9]

(7)

式(7)中有效点导纳包含4部分：a.原点导纳;b.点互耦合;c.传递耦合;d.传递互耦合。

工程实际中一般忽略点互耦合和传递互耦合，仅考虑多点安装的传递耦合的影响，并且由式(7)可知，有效点导纳与激励力的大小和分布有关，本研究采用文献[9]的方法，认为力的分布是均匀的。因此，有效点导纳可以表示为

(8)

将式(5)中的导纳换成有效点导纳，则多输入输出的耦合隔振系统就转化成为多个单输入输出系统，则以任意一隔振器在设备机脚安装点为研究对象，其动力学方程为

(9)

其中：v0为设备机脚的自由振速；vu和vb分别为设备机脚和基座安装点处的振速；fu和fb分别为隔振器作用在设备和基座上的激励力；Hu∑和Hb∑分别为设备机脚和基座安装点的有效点导纳；Z11，Z12，Z21和Z22分别为该隔振器阻抗。以上参数均为标量。

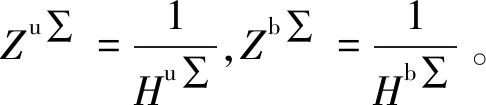
(10)

由式(10)可得

(11)

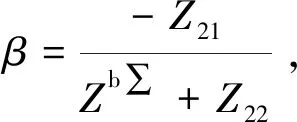
(12)

β与隔振系统隔振效果之间的关系为

(13)

由式(13)可知，隔振效果仅与隔振器和基座的阻抗有关。隔振量Δ越大，则β值越小。对于弹性安装来说，实际工程中设备机脚的有效点阻抗要远大于隔振器的阻抗，即

(14)

由于实际工程中弹性隔振系统的隔振效果一般大于10 dB，由式(12)可得

v0≈vu

(15)

式(15)表明：在弹性安装条件下，在满足式(14)的条件下，设备自由振速近似等于设备机脚的振速。所以，设备的自由振速可通过测量弹性安装设备机脚的振速来获得。

通过式(15)可以获得此推论：当设备采用不同的隔振器时，如果两个隔振系统的隔振效果大于10 dB，则该设备在不同隔振系统中测得的机脚振动速度近似相等，且均等于设备的自由振速。

1.3 误差分析

以下对式(15)的误差进行分析，即在弹性安装条件下，以设备机脚的振速作为设备自由振速时，由式(16)可知误差δ为

(16)

低频条件下可将隔振系统视为刚体模型，设隔振器的额定载荷为M，刚度为K，阻尼为C，阻尼比为ξ，隔振器的固有频率为ωn，则隔振器的原点阻抗Z11与传递阻抗Z12分别为

(17)

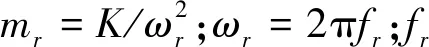
设被隔振设备的质量为Ma，则低频下其阻抗Zu表现为质量阻抗

Zu=jωMa

(18)

若安装N个隔振器，则设备的有效点阻抗Zu∑近似为

(19)

定义α为隔振器的载荷系数，表示隔振器的实际载荷与额定载荷之比。忽略载荷不均匀性，则设备质量与隔振器的额定载荷之间满足

(20)

将式(17)(19)代入式(16)，整理得

(21)

对于隔振系统来说，|β|≪1,ωn≪ωr，由式(21)可知，当激励频率与隔振器的固有频率吻合时(ω=ωn)，误差δ近似为

(22)

2 数值算例

2.1 隔振系统模型

以电机作为机械设备振动源，采用ANSYS软件对隔振系统进行有限元建模计算。电机功率为22 kW，转速为3 000 r/min，质量为156 kg，设备机脚安装4个隔振器，基座以四边简支矩形板模拟。模型材料特性为：弹性模量2.1×1011Pa，泊松比0.3，密度7 850 kg/m3。系统的阻尼比取8%。在设备上施加服从均匀分布的随机载荷，并叠加50 Hz基频的谐波激励(如图2所示)。计算了4种隔振器工况，隔振器的固有频率、刚度、阻尼和载荷如表1所示。

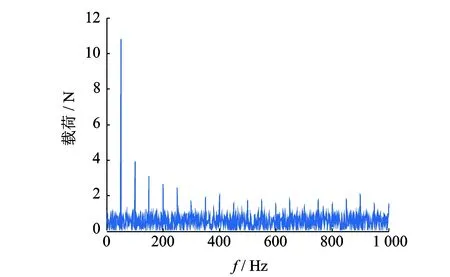
图2 设备随机激励载荷Fig.2 Random force on machine

工况固有频率/Hz刚度/(N·m-1)阻尼/(N·s·m-1)载荷/kg13.52.42×1041765025.04.93×1042515037.09.66×10435250410.01.97×10550350

2.2 隔振系统的阻抗特性

为了分析隔振系统对自由振速的影响，进行隔振器、设备机脚和基座的阻抗特性分析。对于隔振器，驻波频率取为250 Hz，阻尼比取为8%，计算隔振器的原点阻抗和传递阻抗(如图3所示)。在隔振器驻波频率处阻抗最小，高于隔振器驻波频率时，隔振器阻抗主要受隔振器质量的控制。低于驻波频率时，隔振器阻抗主要表现为刚度特性。

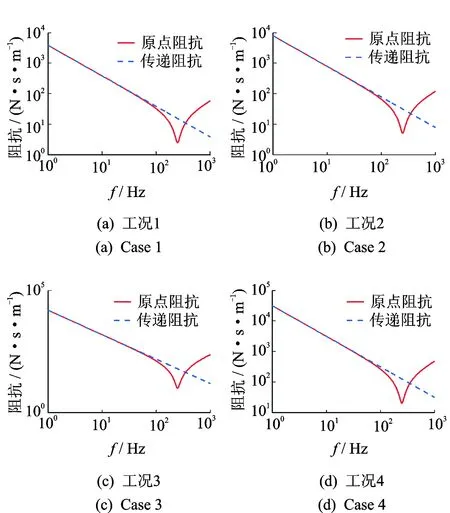
图3 隔振器原点阻抗和传递阻抗(工况1～工况4)Fig.3 Point impedances and transfer impedances of isolations (case 1 to case 4)

根据文献[9]的方法，对于设备和基座，采用有限元模型获得设备机脚与基座安装点的导纳矩阵，然后根据式(6)计算出有效点导纳，从而获得设备与基座的有效点阻抗。设备机脚有效点阻抗、基座有效点阻抗与隔振器阻抗对比如图4所示。在低频范围内，设备机脚的阻抗表现为质量阻抗，甚至小于隔振器的阻抗。对于四边简支的基座板结构，低于第1阶模态频率(61.64 Hz)时，其阻抗表现为刚度阻抗。

2.3 弹性安装条件下设备机脚振速与自由振速

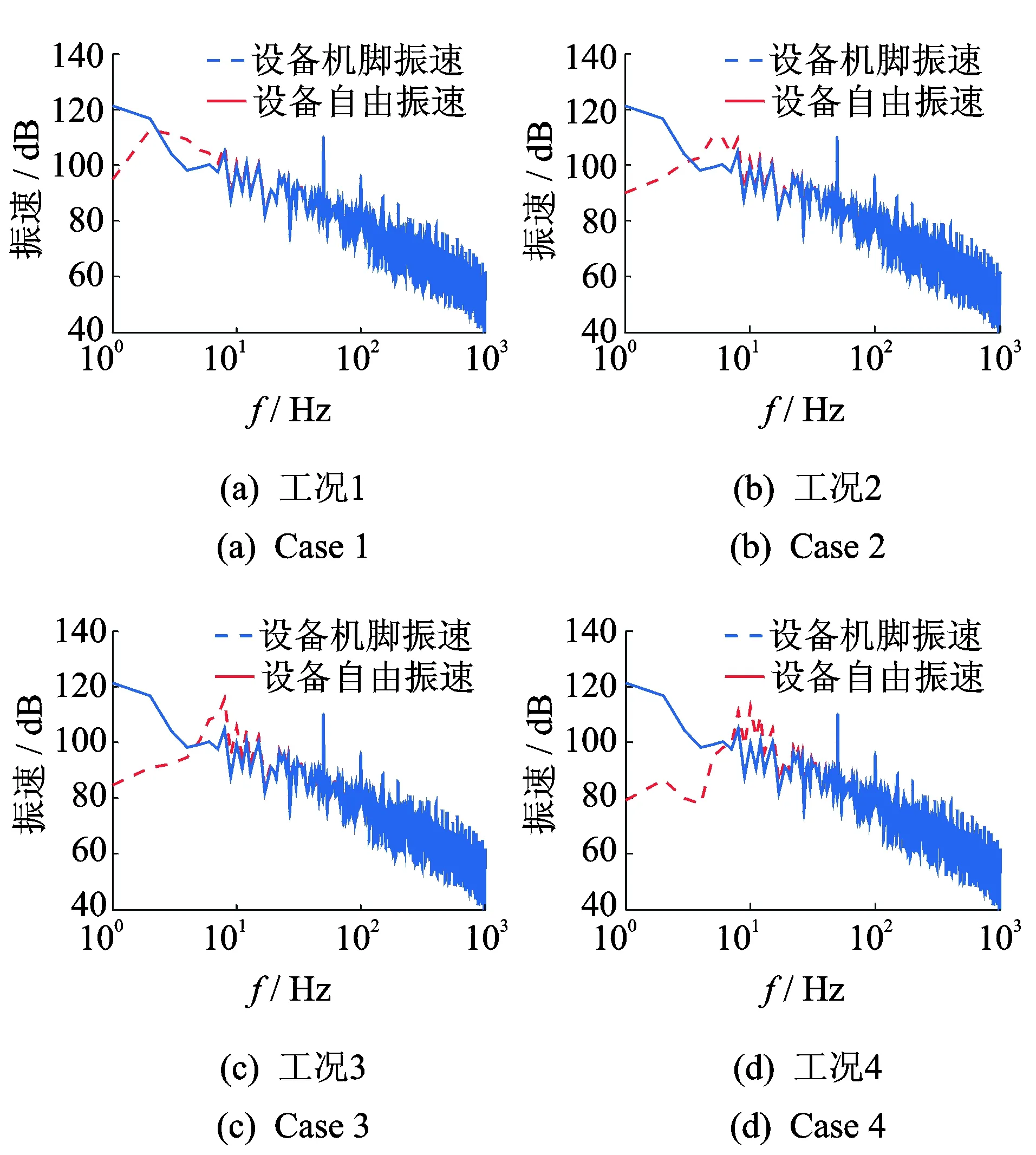
图5 设备自由振速的理论值与有限元仿真值(工况1～工况4)Fig.5 Values of free velocities for theory and simulation (case 1 to case 4)

本研究通过有限元模拟的方法来验证式(15)的正确性。自由振速的模拟方法为：根据其定义，对设备的有限元模型施加自由边界条件和随机激励，计算设备机脚的振速即为自由振速；设备机脚振速的模拟方法为：将设备置于隔振系统中，在隔振系统的有限元模型上施加相同的随机激励，基座采用四边简支边界条件，计算出设备机脚的振速。设备机脚振速与自由振速的4种工况的有限元模拟结果如图5所示。机脚振速与自由振速的差异主要发生低频段，在高频段，机脚振速与自由振速基本一致。

2.4 自由振速测量的误差分析与适用频率范围

将设备机脚振速与自由振速的代数差作为测量误差，图6为4种隔振器工况下的自由振速测量误差曲线，有限元模拟的测量误差与理论测量误差基本一致。最大正向误差发生在系统的垂向共振频率处，共振时弹性安装设备的振速放大，因此，机脚的振速远大于该频率点的自由振速。在低于隔振器固有频率范围内(如图4所示)，由于设备机脚的阻抗小于隔振器的阻抗，此时隔振器对于设备来说相当于是刚性约束，因此，此时设备机脚振速远小于自由振速。在高于隔振器固有频率条件下，随着频率的增加，测量误差逐渐减小，可控制在1 dB内。表2为该测量方法的适用频率范围。从四种隔振器工况

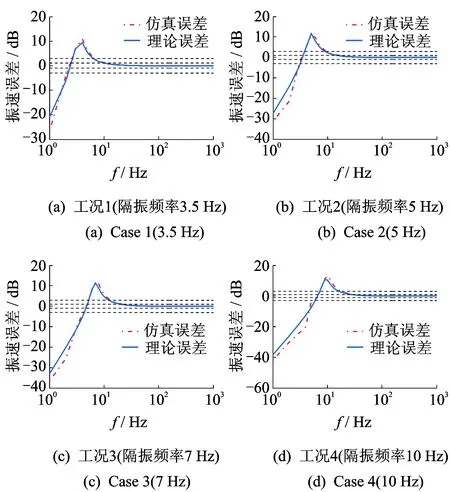
图6 自由振速测量误差(工况1～工况4)Fig.6 Measurement errors of free velocities (case 1 to case 4)

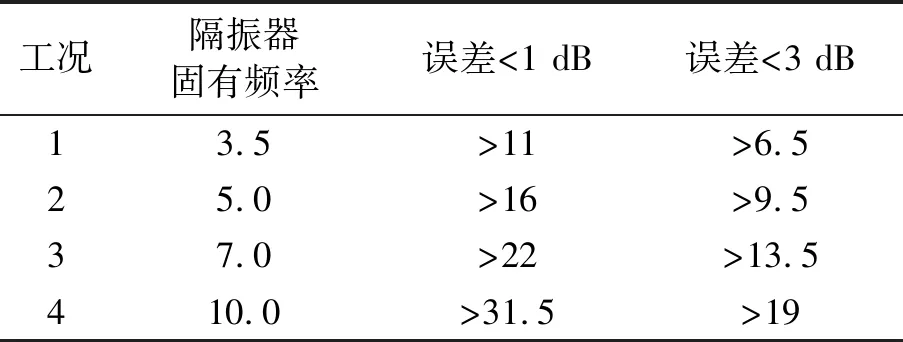
Tab.2 Adaptive frequency ranges of measurement method Hz

来看，隔振频率越低，测量方法的适用频率范围越宽。若控制测量误差在1 dB范围内，测量方法适用的最低频率值约为隔振器固有频率的3倍；若控制测量误差在3 dB范围内，测量方法适用的最低频率值约为隔振器固有频率的2倍。

3 实 验

由于工程实际中设备自由振速的测量难以实施，因此笔者采取间接验证的实验方法，实验装置如图7所示。本实验对变频电机设备进行隔振，分别采用两种型号隔振器，测试频段取10～8 000 Hz，测量了电机在4种转速工况下机脚的振动加速度级和系统隔振效果，各工况转速分别为600,1 200,1 500和2 000 r/min，实测数据如表3所示。

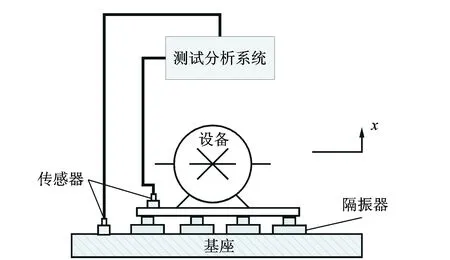
图7 实验示意图Fig.7 Experimental diagram

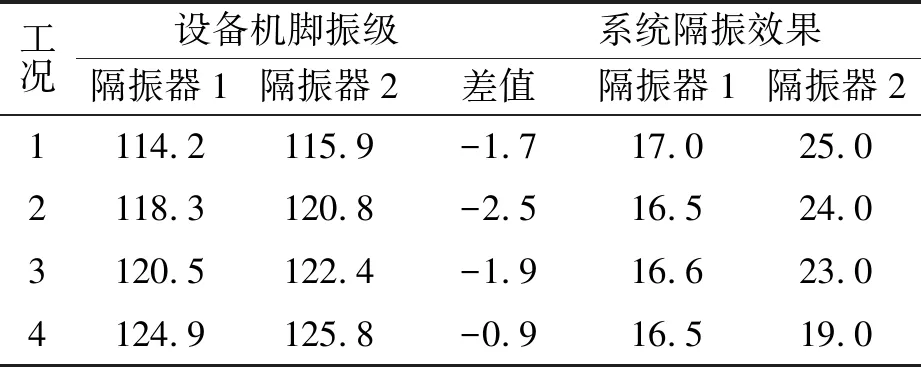
Tab.3 Vibration level of machine and system isolation efficiency under four cases dB

实验数据表明，4种电机转速下，两种隔振系统中的电机机脚振级在测量频段内的差异为0.9～2.5 dB，此时，两种隔振系统的隔振效果均大于10 dB。误差可能主要是测点位置的差异造成的。因此，如果不计测点位置影响和测量误差，可认为设备机脚的振级与隔振器无关，且为常数，即近似等于设备的自由振速。该实验结论验证了文中1.2节的理论推论，间接验证了式 (15)。

4 结 论

1) 在弹性安装条件下，当系统的隔振效果大于10 dB时，设备自由振速近似等于设备机脚振速。

2) 自由振速可通过单层弹性安装的方式获得。设备机脚的阻抗特性对自由振速的测量结果影响较大，系统的隔振效果对自由振速测量的影响要小于设备机脚阻抗特性的影响。

3) 考虑到实际工程中的测量误差一般为1 dB，误差分析表明，当设备机脚与基座阻抗远大于隔振器阻抗时，弹性安装条件下测量设备自由振速的适用频率范围为大于3倍的隔振器固有频率。

4) 本研究工作对自由振速的获取以及机械设备振动源特性的转换研究具有一定的理论价值和工程应用前景。