基于FLUENT的压电式无针注射器喷嘴射流分析*
2019-05-09张铁民李晟华
张铁民, 李晟华, 梁 莉, 梅 园
(华南农业大学工程学院 广州,510642)
引 言
在禽畜防疫中,养殖户常通过手动进给式有针连续注射器对畜禽实施免疫接种,存在着注射针安装步骤繁琐、对注射者使用要求高、药液被细胞吸收时间较长和注射废弃物处理难等问题[1]。无针注射利用动力产生的瞬时高压将安瓿瓶内的药液从喷嘴挤压形成高速、高压的喷射流(流速大于100 m/s),射流的压力足以刺破皮肤,从而击穿皮肤并实现皮下给药[2]。与有针注射相比,无针注射具有以下优势:a.注射时几乎无疼痛感;b.皮下注射对组织细胞损伤较少;c.药物以扩散状进入体内,更容易被细胞吸收;d.操作简单,使用前只需要接受短时间的培训;e.不需要更换针头,避免疾病交叉感染,同时降低医疗垃圾处理的成本[3]。
目前,无针注射器的动力源可为压缩弹簧、高压气体、激光和电磁动力等[4-5]。其中,压电式无针注射器基于压电材料的逆压电效应,以压电驱动器作为动力源,在电压信号作用下产生变形推动活塞运动,从而使药液从喷嘴喷射而出。由于压电材料的输出位移与外加电场强度基本为线性关系[6],能对喷射过程进行精确控制。与音圈电机相比,压电驱动器的响应时间短,位移分辨率高,结构紧凑,无需齿轮减速机构便可直接驱动[7],尤为适合作为无针注射器的动力源。Stachowiak等[8]利用压电致动器加速纳升级(50~650 nL)流体到足够的速度(60~160 m/s)进行皮肤渗透和药物输送,并通过一系列的试验研究喷射速度、撞击压力、注射剂量和渗透深度之间的关系。Arora等[9]也设计了一款纳升级(2~15 nL)脉冲调制式压电微注射器,用于透皮传送生物大分子。
喷嘴作为无针注射器的关键部件,它的结构决定了高压自由射流的流场特性和无针注射的效果,目前尚未有文献对压电式无针注射器的喷嘴射流进行设计和分析。基于粘性不可压缩流体的纳维-斯托克斯方程(Navier-Stokes equations,简称N-S方程),笔者利用计算流体动力学软件Fluent的Realizablek-ε湍流模型和流场体积函数(volume of fluid,简称VOF)多相流模型,对4种结构的喷嘴高压自由射流进行数值计算,并利用正交试验法分析喷嘴的结构参数对喷嘴出口截面的喷射速度和湍流强度的影响规律,从而设计一种射流特性较好并适用于压电式无针注射器的喷嘴结构。
1 高压自由射流
高压自由射流过程如图1所示,它由初始段、主体段和扩散段三部分构成,射流沿半径方向流速逐渐减小,沿轴向方向整体动能逐渐降低[10]。等速核位于喷嘴出口,整体为锥形结构,由纯液相流组成,其流线为平行直线,同一截面处速度相等,且在各个区域中能量最大[11],射流在等速核阶段注入皮肤消耗能量最小,且便于控制[12]。为了提高射流的可控性,喷嘴喷射的液体断面流速应分布均匀,轴线速度衰减较慢。
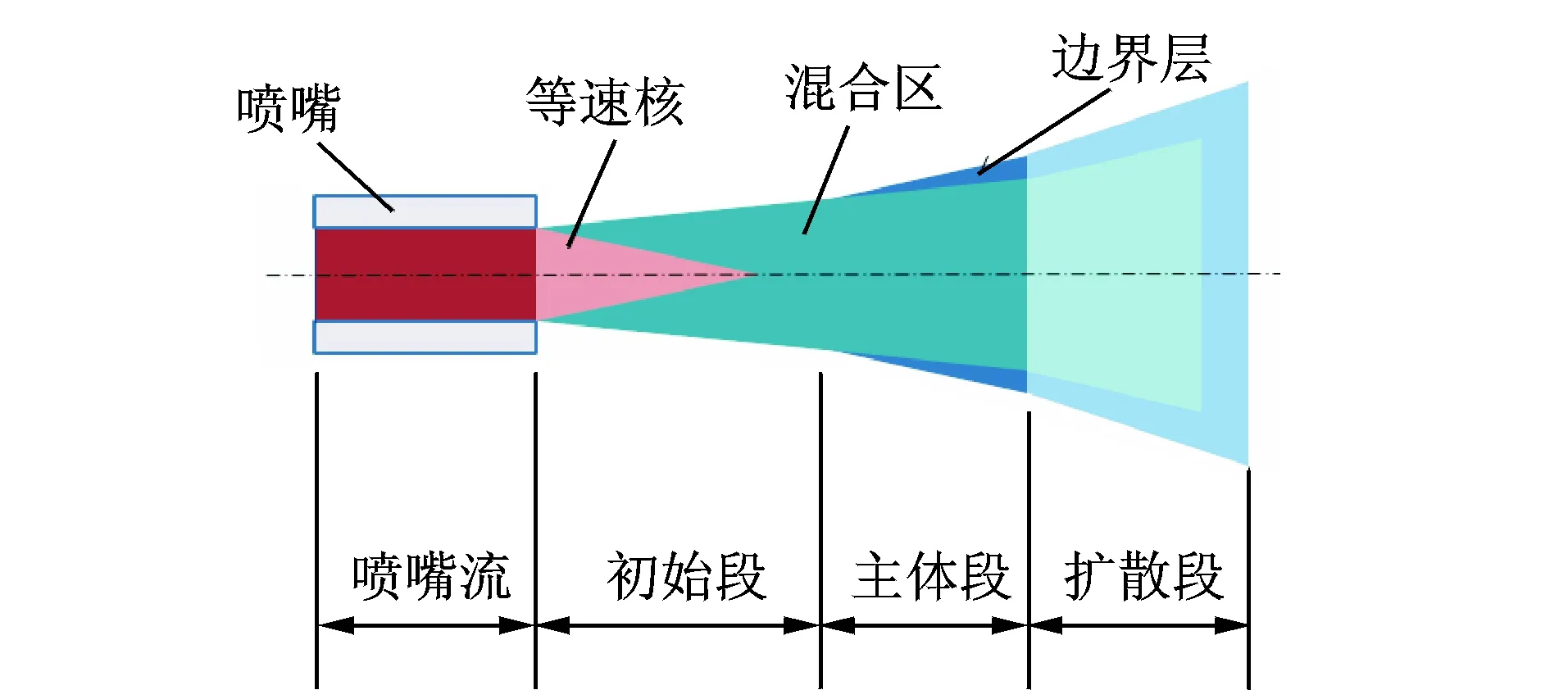
图1 高压自由射流过程Fig.1 Process of high pressure free jet
2 喷嘴的结构模型
为获得集中和对称分布的自由射流,一般采用针形喷嘴结构[13],如图2所示。其中空白部分为液体流道,射流方向如黄色箭头所示。为使射流喷射参数在不同喷嘴结构上形成对比,故各喷嘴流道入口直径保持一致,锥形喷嘴(图2(b))和锥柱形喷嘴(图2(c))的出口半径为圆柱形喷嘴(图2(a))和锥柱扩散形喷嘴(图2(d))的一半,各针形喷嘴的结构参数选定如表1所示。
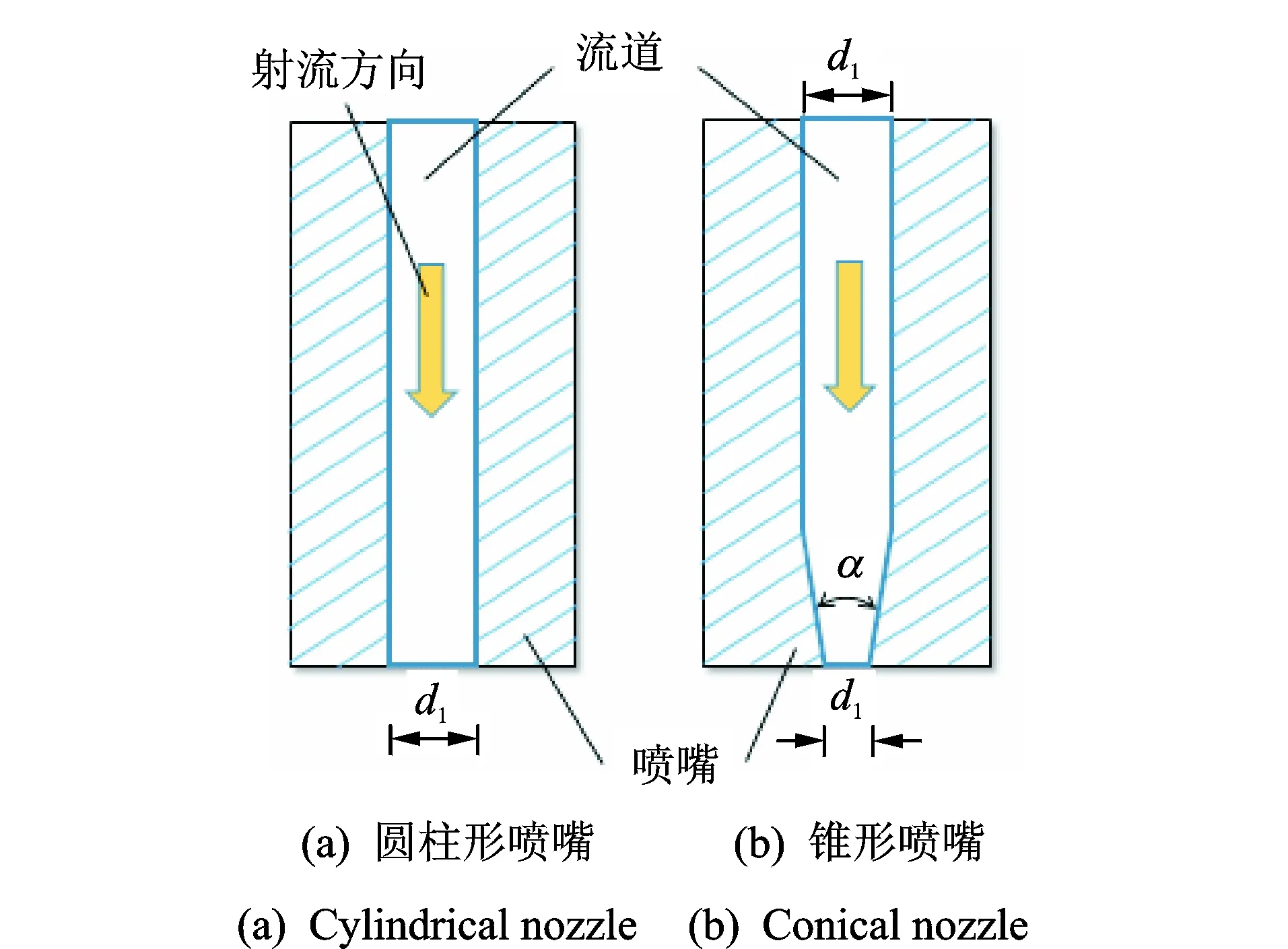
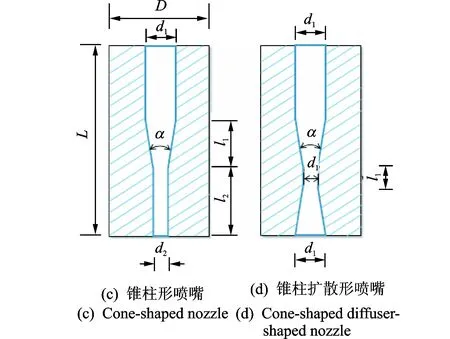
图2 针形喷嘴结构Fig.2 Structure of needle-shaped nozzles
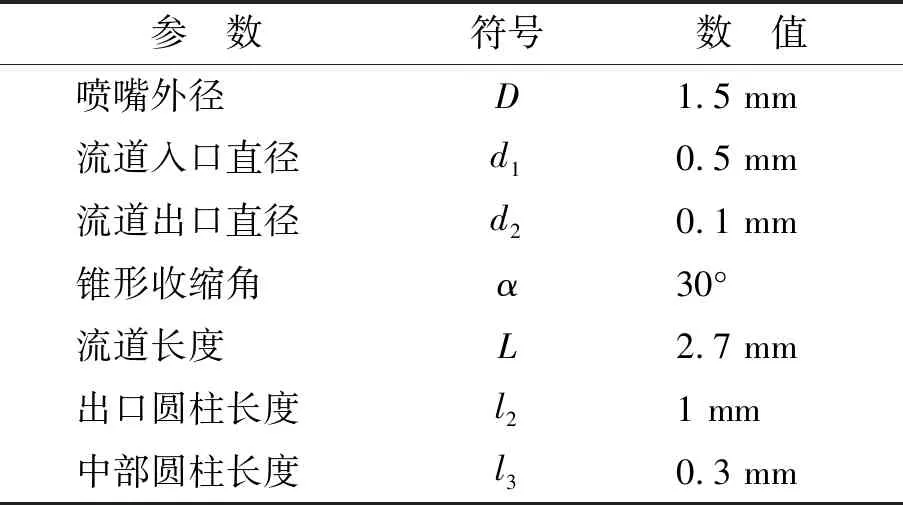
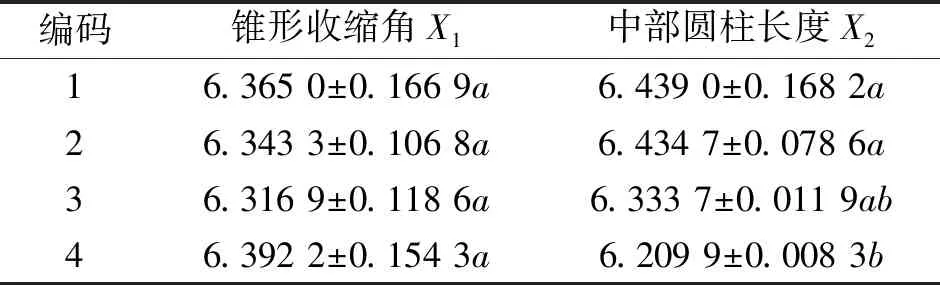
参 数符号数 值喷嘴外径D1.5 mm流道入口直径d10.5 mm流道出口直径d20.1 mm锥形收缩角α30°流道长度L2.7 mm出口圆柱长度l21 mm中部圆柱长度l30.3 mm
3 喷嘴的流场分析
为简化研究喷嘴结构对喷射截面速度、湍流强度和射流形态的影响,忽略皮肤对射流的影响,利用计算流体力学软件Fluent对不同结构的喷嘴高压自由射流进行模拟。
3.1 流场有限元网格模型
圆柱形喷嘴二维流场模型如图3所示,笛卡尔坐标系设于喷嘴出口处,x轴正方向为喷嘴径向,y轴正方向为喷嘴轴向,坐标轴原点位于喷嘴出口圆心位置。其中,区域I代表圆柱形喷嘴的内流道,区域Ⅱ代表喷嘴射流出口空气计算域,尺寸为10 mm×20 mm。为准确捕足喷嘴内流道及出口处的流场特性,设定喷嘴内流道的网格密度为0.05 mm,在喷嘴出口处进行三级细化,并采用混合网格对整个模型进行划分,最终得到模型的网格数为4 803,节点数为4 606。
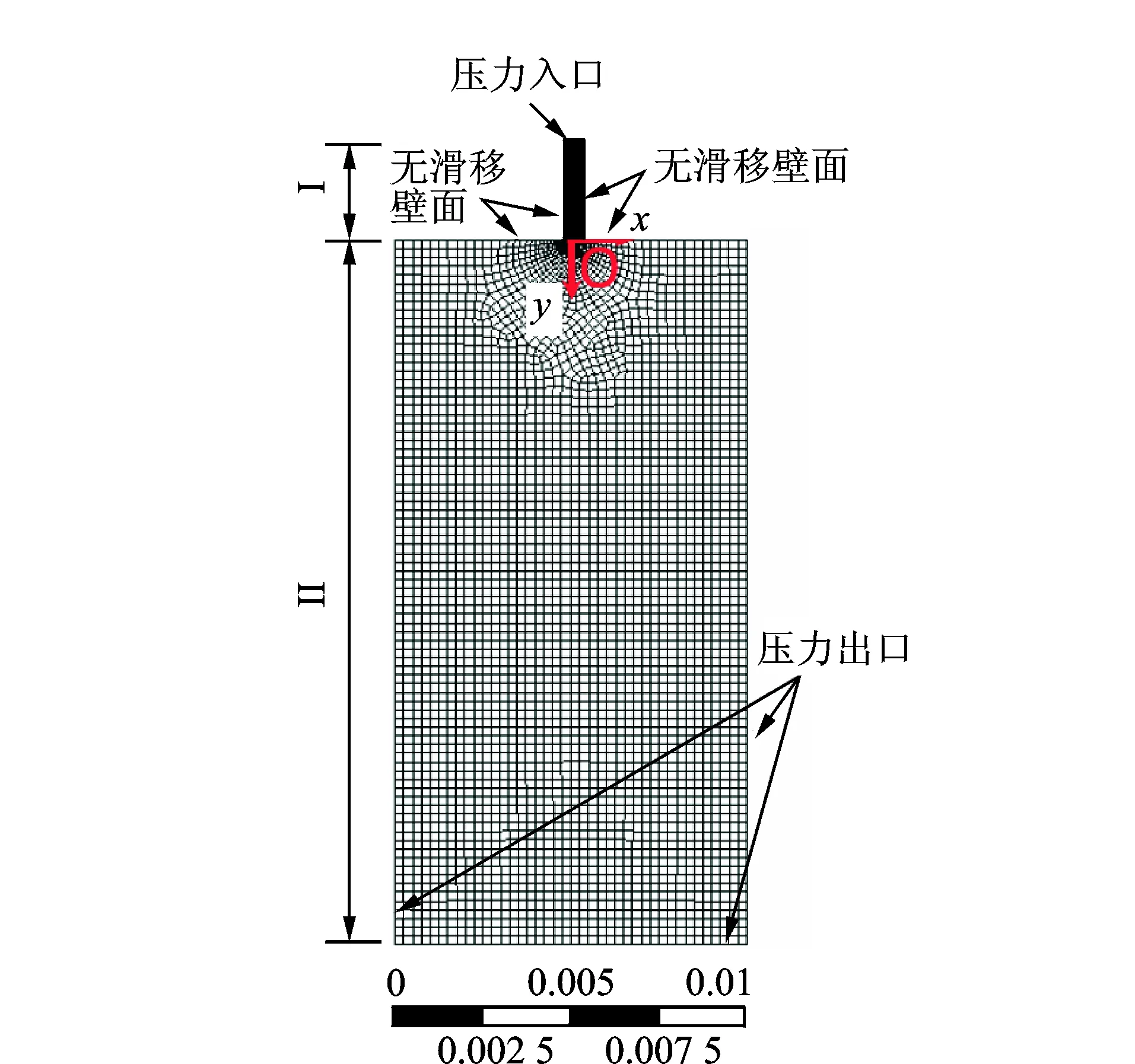
图3 圆柱形喷嘴的二维流场模型(单位:m)Fig.3 2D flow field model of cylindrical nozzle(unit:m)
3.2 数学模型
3.2.1 基本方程
黏性不可压缩流体的流动遵循N-S方程,其连续方程为
(1)
其中:ρ为液体密度(kg/m3);t为时间(s);xi为流体在i方向的坐标位置(m);ui为速度矢量在i方向的投影(m/s)。
动量方程为
(2)
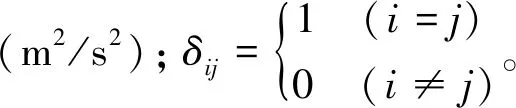
3.2.2 湍流模型
Realizablek-ε模型适合多种流动类型,包括自由流(射流和混合层)、腔道流动和边界层流动,特别对于轴对称喷嘴射流,能给出较好的射流扩张角,因此采用该模型来封闭N-S方程组,其湍动能k及其耗散率ε的输运方程[14-15]为
其中:Gk表示由于平均速度梯度而产生的湍动能
Gk=μtS2
(5)
(6)
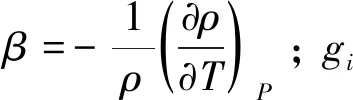
系数C1和C2的取值如下
(7)
其中:η=Sk/ε。
(8)
其中:η0=4.38。
3.2.3 多相流模型
VOF多相流模型中不同的流体组分共用一套动量方程,通过计算流体体积分数Fα追踪各流体组分的流量,从而构造自由面形状。Fα为单元内第α相流体所占体积与该单元总体积之比,满足以下方程
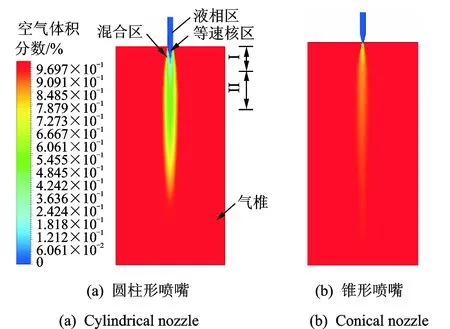
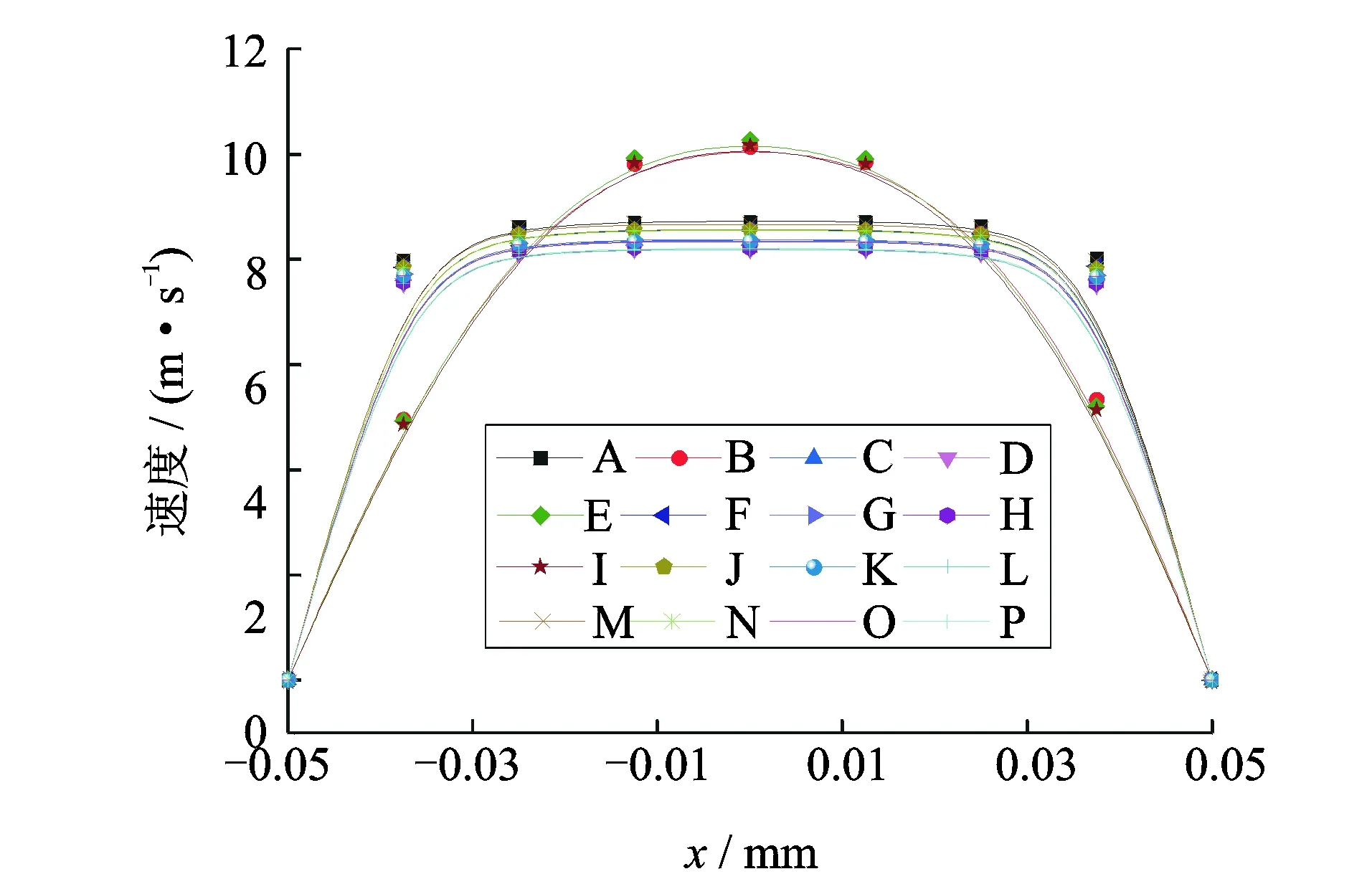
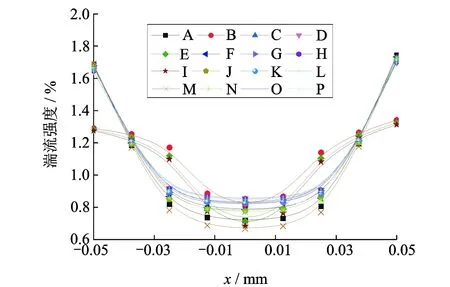
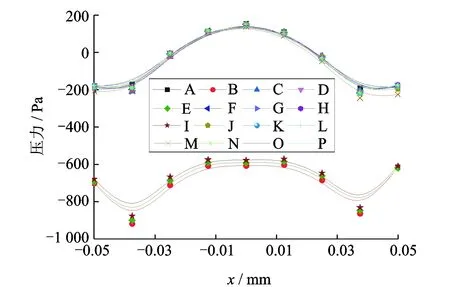
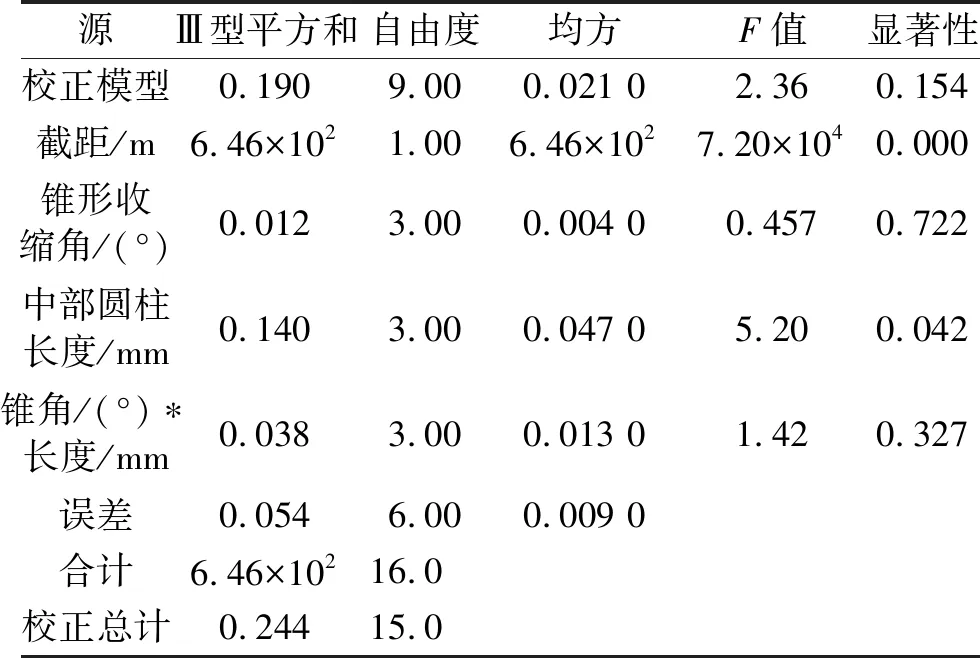
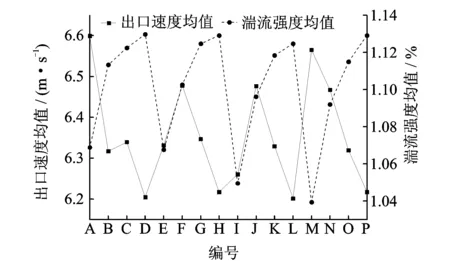
当Fα=0时,单元内不含第α相流体;当Fα=1时,单元内只含第α相流体;当0 ϑ=∑ϑαFα (11) 其中:ϑα为单元内各相流体的属性参数。 利用Fluent软件进行气液两相流体动力学计算时,边界条件设置和假设如下: 1) 二维模型的出入口分别设置为压力入口和压力出口,由所设计的压电驱动器可得,入口处的相对压强为405 66 Pa,出口处的相对压强为0 kPa,全局的参考压强为101.325 kPa,不考虑两相流之间的能量交换,所有的壁面均为无滑移壁面; 2) 考虑实际作业时,射流由上往下喷射,因此增加重力作用,并将重力加速度设置为9.8 m/s2,方向为y轴正方向; 3) 为获得精确的瞬态动力学特性,时间步长设为1×10-4s,计算时间步为20,出入口的初始湍流强度的计算公式[15]为I=0.16Re-1/8,其中:I为湍流强度,%;Re为雷诺数,Re=Udρ/μ;U为入口速度(m/s);d为喷嘴出口水力直径(m); 4)多相介质的主相为理想空气、第二相为液态水,其物理特性如表2所示。 表2 多相介质的物理特性 3.4.1 射流形态 图4 4种结构喷嘴在空气中的射流形态Fig.4 Jet shapes of four kinds of nozzles in the air 不同结构喷嘴在空气中射流形态如图4所示,其中红色部分为气相区,空气体积分数为0%,蓝色部分为液相区,空气体积分数为100%,其他部分为两相混合区,空气体积分数介于0~100%之间。由图4(a)圆柱形喷嘴的射流形态分为射流初始段Ⅰ和主体段Ⅱ,且由纯液相流体组成的等速核呈倒锥形,与张雷等[16]的实验形态相吻合。图4(b)~4(d)分别为锥形喷嘴、锥柱形喷嘴和锥柱扩散形喷嘴的射流形态图。其中,由于锥柱形扩散喷嘴的内流道急剧变化,导致其射流形态呈现非对称性。 3.4.2 喷射速度 4组喷嘴出口截面的喷射速度分布曲线如图5所示,从图5中看出,圆柱形喷嘴和锥柱形喷嘴的出口速度符合泊肃叶流动规律,即对称分布且中部流速最高,分别可达9.0和8.0 m/s,靠近壁面附近的流速趋于零。锥形喷嘴的最高流速偏于喷嘴左侧,锥柱形喷嘴的喷射速度出现3个极值,分别在-2×10-4m,-1.4×10-4m,7.5×10-5m,其原因在于喷嘴出口形状变化过于剧烈,导致外界空气涌入喷嘴内,影响喷嘴内流体流速。 3.4.3 湍流强度 图6 4组喷嘴的湍流强度分布曲线Fig.6 Turbulence intensity distribution curve of four groups of nozzles 4组喷嘴出口截面的湍流强度分布曲线如图6所示。湍流强度是湍流强度涨落标准差和平均速度的比值,可直接反映湍流的相对强弱。从图中可以看出,圆柱形喷嘴和锥柱形喷嘴的湍流强度分布均为壁面附近较大,中部较小的规律,其中前者的湍流强度最小,为0.15%,液体流动趋于层流,后者的最小湍流强度为0.85%,均属于低湍流强度范围。锥形喷嘴和锥柱扩散形喷嘴的最小湍流强度均偏离喷嘴中部,其中后者湍流强度出现大幅波动,说明其液流可控性较差。 3.4.4 喷射压力 4组喷嘴出口截面的喷射压力分布曲线如图7所示,由图7可见,锥形喷嘴的喷射压力远大于其他喷嘴,其最大喷射压力分别为圆柱形喷嘴、锥柱形喷嘴和锥柱扩散形喷嘴最大喷射压力的15.3倍、54.4倍和2 041.2倍。 图7 4组喷嘴的喷射压力分布曲线Fig.7 Injection pressure distribution curve of four groups of nozzles 综上所述,锥形喷嘴内压力耗损较少,喷射压力较大,但喷射速度和湍流强度分布在喷嘴中部均非最佳值,而圆柱形喷嘴和锥柱形喷嘴则与此相反。可见,选定合适的锥柱形喷嘴结构参数能得到较佳的射流特性。 保持边界条件和锥柱形喷嘴直径不变,分析该喷嘴的锥形收缩角α和中部圆柱长度l2对喷嘴出口截面射流特性的影响,以期得到对称的射流、较高的喷射出口压力和较低的喷嘴出口湍流强度。选取各参数因素水平值如表3所示。 表3 各参数因素水平编码值 为分析锥形收缩角、中部圆柱长度及其交互作用对喷嘴出口截面射流特性的影响,特编制三因素四水平正交表L16(43)进行仿真分析。表4为仿真分析设计方案。表中“收缩角*长度”表示锥形缩角和中部圆柱长度的交互作用。 表4 喷嘴结构流场仿真分析设计方案 Tab.4 Simulation design of flow field in nozzle structure 编号锥形收缩角/(°)中部圆柱长度/mm收缩角/(°)∗长度/mmA111B122C133D144E212F221G234H243I313J324K331L342M414N423O432P441 16组锥柱形喷嘴出口喷射速度、湍流强度分布和喷射压力分布分别如图8~10所示。 图8 16组喷嘴出口的喷射速度分布曲线Fig.8 Jet velocity distribution curve of 16 groups of nozzles 图9 16组喷嘴的湍流强度分布曲线Fig.9 Turbulence intensity distribution curve of 16 groups of nozzles 图10 16组喷嘴的喷射压力分布曲线Fig.10 Injection pressure distribution curve of 16 groups of nozzles 由图10可见,这16组喷嘴根据曲线发展趋势可大致分为i和ii两类,其中编号分别为B,E和I的喷嘴可归为i类。从出口喷射速度分布来看,i类喷嘴的出口喷射速度分布呈椭圆形,且喷嘴中部与壁面速度差较大;从湍流强度分布来看,i喷嘴出口中部的湍流强度与ii类喷嘴不相上下,但壁面附近的湍流强度较高;从喷嘴出口喷射压力来看,ii类喷嘴出口喷射压力比i类喷嘴的高,且后者压力值均为负值,引起空气进入喷嘴,影响注射效果。因此,ii类喷嘴总体上优于i类喷嘴。在三个射流特性指标中,喷嘴速度和湍流强度对注射效果影响较大[17]。表5和表6分别为利用统计分析软件SPSS对16组编号喷嘴出口平均速度所绘方差分析与均值标准对比。 表5 正交仿真分析速度均值方差分析表 Tab.5 Orthogonal simulation analysis of mean velocity variance 源Ⅲ型平方和自由度均方F值显著性校正模型0.1909.000.021 02.360.154截距/m6.46×1021.006.46×1027.20×1040.000锥形收缩角/(°)0.0123.000.004 00.4570.722中部圆柱长度/mm0.1403.000.047 05.200.042锥角/(°)∗长度/mm0.0383.000.013 01.420.327误差0.0546.000.009 0合计6.46×10216.0校正总计0.24415.0 表6 正交仿真分析速度均值标准差比对表 Tab.6 Orthogonal simulation analysis of mean velocity of the standard deviation 单位:m/s 采用Duncan′s multiple range test方法分析,同一列不同字母表示显著性差异。其中小写字母代表是在 0.05 水平下比较,差异显著 由表5和表6可知,喷嘴结构参数对喷嘴出口速度均值影响显著性依次为:中部圆柱长度、锥形收缩角与中部圆柱长度的交互作用、锥形收缩角。其中,中部圆柱长度的显著性小于0.05,即其对喷嘴出口平均速度有显著影响;锥形收缩角与中部圆柱长度的交互作用、锥形收缩角的显著性均大于0.05,即二者对喷嘴出口平均速度无显著性影响。鉴于喷嘴出口速度越大,则注射器的穿透能力越强,因此最佳尺寸组合为X14X21。 表7和表8分别为利用统计分析软件SPSS对16组编号喷嘴出口平均速度所绘方差分析与均值标准对比。 由表7和表8可知,喷嘴结构参数对喷嘴出口湍流强度均值影响显著性依次为:中部圆柱长度、锥形收缩角、锥形收缩角与中部圆柱长度的交互作用。其中,中部圆柱长度和锥形收缩角的显著性均小于0.05,即二者对喷嘴出口平均湍流强度有显著影响;锥形收缩角与中部圆柱长度的交互作用的显著性大于0.05,即其对喷嘴出口平均湍流强度无显著性影响。鉴于喷嘴出口湍流强度越小,则注射器的射流可控性越好,因此最佳尺寸组合为X14X21。 表7 正交仿真分析湍流强度均值方差分析表 Tab.7 Orthogonal simulation analysis of mean turbulence intensity variance 源Ⅲ型平方和自由度均方F值显著性校正模型0.0139.0000.00155.6000.000截距/mm19.401.0019.407.40×1050.000锥形收缩角/(°)0.0013.0000.0007.4900.019中部圆柱长度/mm0.0123.0000.004157.0000.000锥角/(°)∗长度/mm0.0003.006.70×10-52.5500.152误差0.0006.002.60×10-5合计19.40016.00校正总计0.01315.00 表8 正交仿真分析湍流强度均值标准差比对表 Tab.8 Orthogonal simulation analysis of mean turbulence intensity of the standard deviation % 采用Duncan′s multiple range test方法分析,同一列不同字母表示显著性差异。其中小写字母代表是在 0.05 水平下比较,差异显著 图11 16组喷嘴的出口速度均值与湍流强度均值变化曲线图Fig.11 Mean value of velocity and turbulence intensity of the nozzle 图11为16组喷嘴的出口速度均值与湍流强度均值变化曲线图。从图中可以看出,当尺寸组合为X14X21时,即锥形收缩角为30°,中间圆柱长度为0.2 mm,编号为M的喷嘴可得到较佳的射流特性,此时出口速度均值为6.56 m/s,湍流强度均值为1.04%。 1) 采用Fluent分析软件模拟所得到的射流形态与张雷的实验形态相吻合,说明了笔者所建立模型及相关设置的正确性。 2) 通过仿真分析,相较于圆柱形喷嘴、锥形喷嘴和锥柱扩散形喷嘴,锥柱形喷嘴的射流可控性较好,能得到对称分布的射流形态。 3) 利用SPSS软件对仿真结果进行分析发现,中部圆柱长度对喷嘴的平均喷射速度和平均湍流强度具有显著影响,锥形收缩角对前者无显著影响,而对后者具有显著影响,中部圆柱长度和锥形收缩角的交互作用对前者和后者均无显著影响。 4) 通过对锥柱形喷嘴的结构参数进行优化分析,发现当锥形收缩角为30°,中间圆柱长度为0.2 mm时,锥柱形喷嘴可得到较佳射流特性,此时出口平均速度可达6.56 m/s,湍流强度均值为1.04%。3.3 边界条件

3.4 结果比较与分析
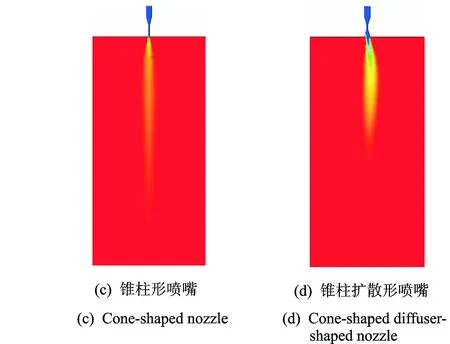
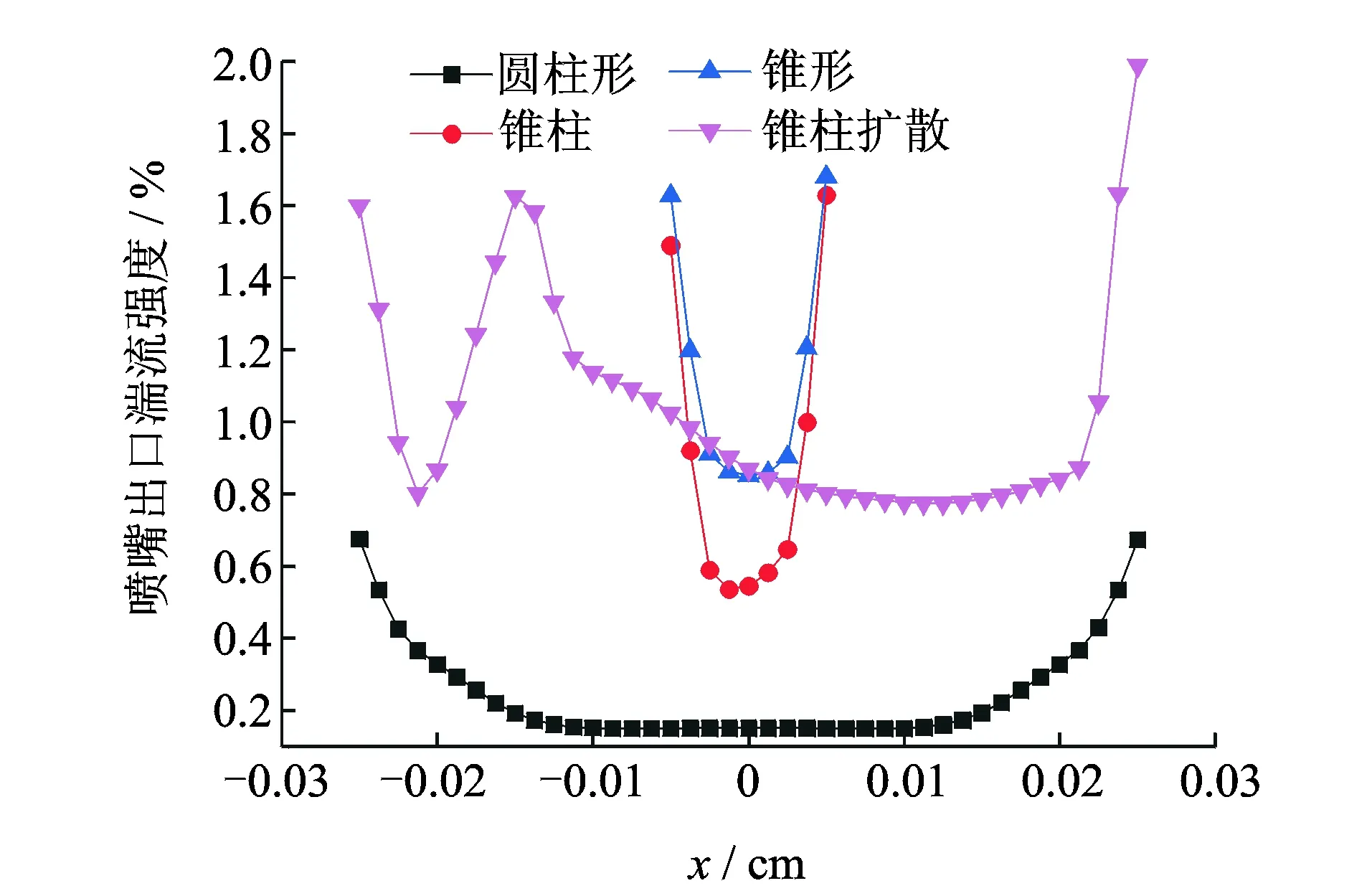
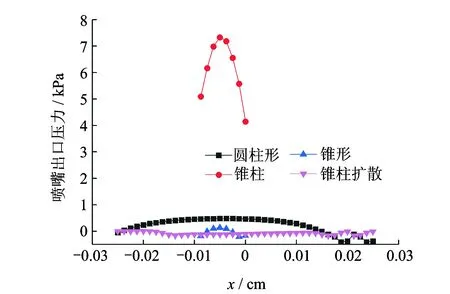
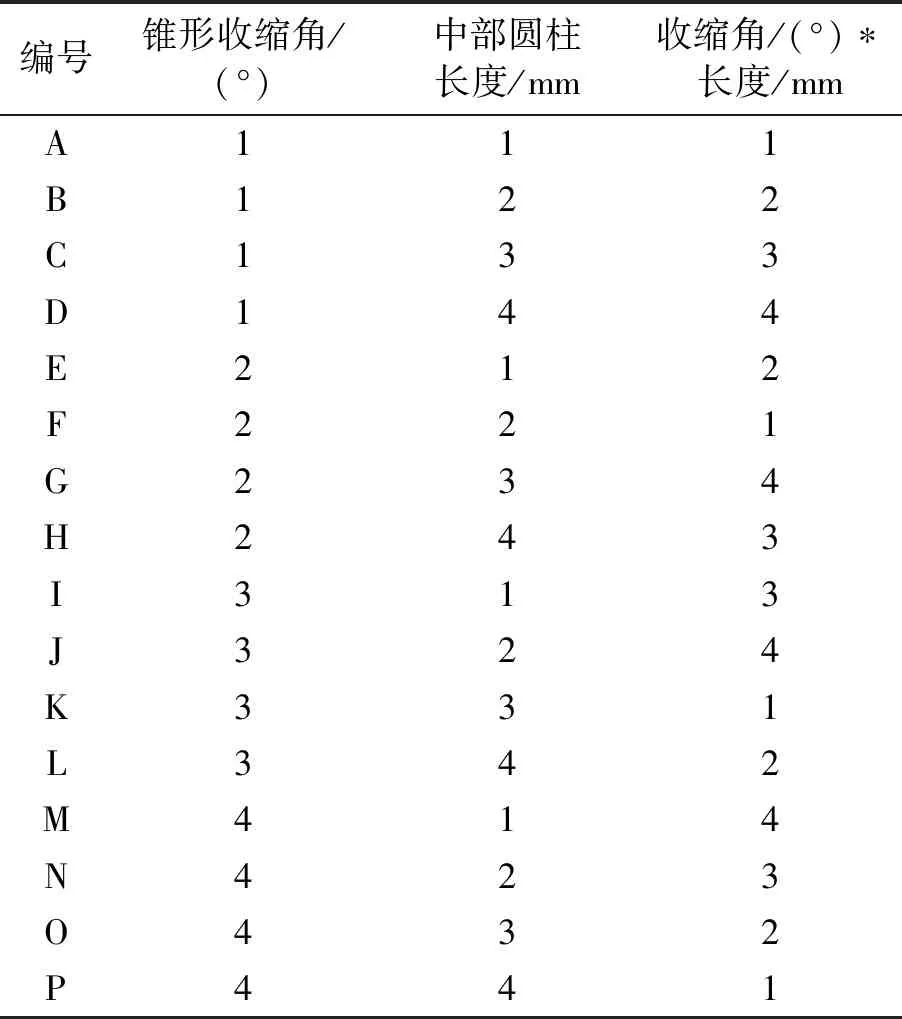
4 喷嘴结构参数对射流特性的影响



5 结 论
