车载移相全桥DC-DC 变换器的设计与仿真
2019-05-09何德威
何德威,石 春,吴 刚
(中国科学技术大学 信息科学技术学院,合肥230026)
近年来,由于环境污染、化石能源短缺等问题日益突出,以电动汽车为代表的新能源汽车受到了人们的关注,且发展迅速,对电动汽车车载电力电子设备的研究也方兴未艾。 针对电动汽车车载高低压直流变换器(DC-DC)的研究则是车载电力电子技术的重点, 考虑到电动汽车越来越严苛的能耗要求、车载情况下复杂的电磁环境以及逐渐增加的电附件,对电动汽车车载DC-DC 变换器在效率、抗干扰、大功率等方面提出了越来越高的标准。
移相全桥PSFB(phase-shift full bridge)拓扑,采用外加电感与开关管寄生电容(或并联电容)谐振的方式实现软开关技术,在高频应用时相比全桥拓扑能极大地提高效率,同时能够适用于大功率的应用场合。 而传统PSFB 变换器的控制器往往采用模拟IC 芯片搭配分立元器件来实现功能, 相比之下,数字控制系统具有控制回路简洁、抗干扰能力强的优点, 并且数字控制芯片兼有实时通讯等接口,能够满足车载环境下实时监控与通讯等需求。
Saber 软件在器件仿真方面具有拟合程度高、收敛性能好、 仿真速度快等优点;MatLab/Simulink则可提供算法设计方面的支持, 能够以C/C++语言实现S 函数,满足对软件层面的模拟。通过Saber 中提供的Saber-Simulink 联合仿真机制,在两者间通过设置合适的采样步长,便可实现两者的联合仿真[1],从而优势互补。
综上,在此以数字控制的移相全桥DC-DC 变换器为研究的对象,在分析其结构原理得到二阶传递函数数学模型的基础上, 进行频域分析与数字PID控制器设计。
1 移相全桥结构的分析与建模
PSFB 拓扑结构如图1 所示。 图中,变压器原边二极管D1—D4为开关管Q1—Q4内部并联的体二极管;C1—C4为开关管Q1—Q4寄生电容或外接电容;Lr为谐振电感,包括主变压器自身漏感;变压器副边DR1和DR2为整流二极管;Lleak1和Lleak2为变压器副边等效漏感;Lf为输出滤波电感;Co为滤波电容;Ro为输出负载。
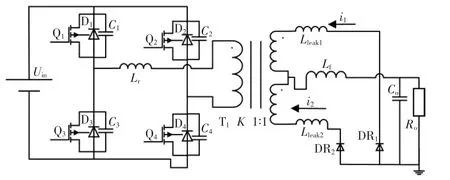
图1 移相全桥结构Fig.1 PSFB structure
其中,Q1,Q2组成超前桥臂;Q3,Q4组成滞后桥臂。 同一桥臂上下开关管驱动波形为180°互补导通(忽略死区时间),超前臂(Q1,Q2)驱动波形超前滞后臂(Q3,Q4)若干角度即占空比(移相角)D,调整D 可以改变变压器原边输入方波u1的宽度, 如图2 所示。 方波u1经过变压器降压、全波整流、LC 滤波后得到直流输出。
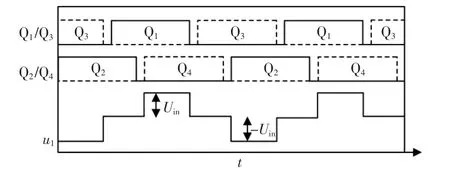
图2 变压器原边输入波形Fig.2 Input waveform of transformer primary side
在忽略原边谐振电感的影响,将开关管与变压器理想化的情况下,根据图2,变压器原边输入电压u1为受占空比D 控制的方波,如图3(a)所示;输入方波u1再经过变压器降压、整流后接入LC 滤波器,如图3(b)所示;此时PSFB 电路可等效为幅值u1/K的直流输入, 占空比为D 的降压式变换Buck 电路如图3(c)所示。 而在满足小纹波假设、低频假设、小信号假设的情况下,Buck 电路的小信号模型如图3(d)所示。 综上,在忽略谐振电感、器件理想化的情况下, 可以采用Buck 电路的小信号模型来指导分析PSFB 电路。
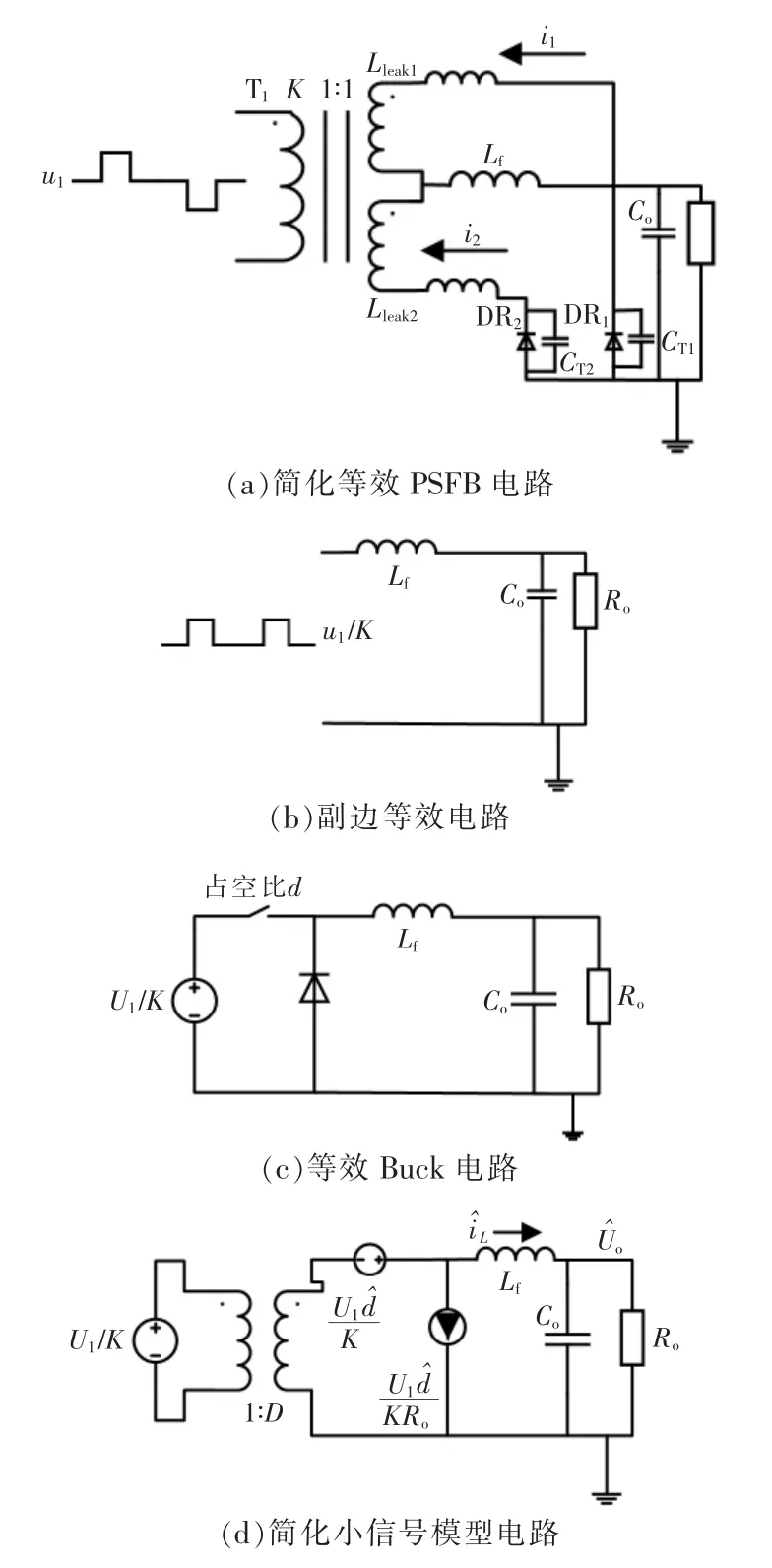
图3 简化移相全桥小信号模型Fig.3 Simplified PSFB small signal model
但考虑到谐振电感的影响,在负载较重时会出现副边得到的方波u2占空比Dsec明显小于原边输入方波的占空比D 的现象,如图4 所示。 图中,u1为变压器原边输入电压,u2为变压器副边电压,i1为原边输入电流。
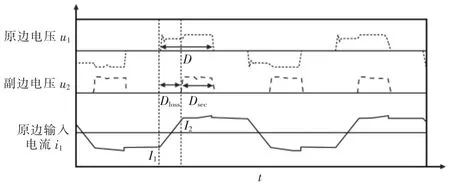
图4 原副边占空比对比Fig.4 Comparison of duty cycle between original side and secondary side
占空比的丢失是因为原边电流i1在换流过程(电流方向反向时)时,谐振电感Lr导致电流不能突变,出现i1小于负载电流的阶段(即图中虚线部分),此阶段内变压器副边处于短路状态,整流二极管DR1和DR2同时导通,负载自然续流,直至原边电流重新提供负载电流。 副边丢失的占空比为

因此PSFB 拓扑应在所述Buck 电路模型的基础上考虑占空比丢失的影响。 占空比丢失的时间为图4 所示原边输入电流由-I1变化至I2的时间,副边实际有效占空比deff应为[2]
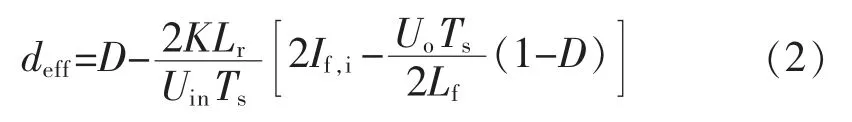
式中:deff为副边有效占空比;D 为原边给定占空比;K 为变压器变比;Lr为谐振电感;Uin为输入额定电压;Ts为开关周期;If,i为输出滤波电感Lf的电流峰值;Uo为输出电压;Lf为输出滤波电感。 由式(2)可知,对于给定的电路参数,有效占空比deff只受If,i,Uin,D 三者的影响,只要求出有效占空比代 入所分析的Buck 电路小信号模型中的就可以得到PSFB 电路的小信号模型。 而由式(2)可得
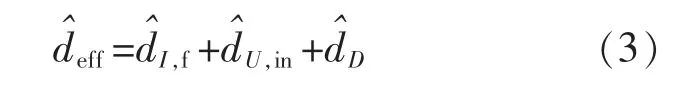
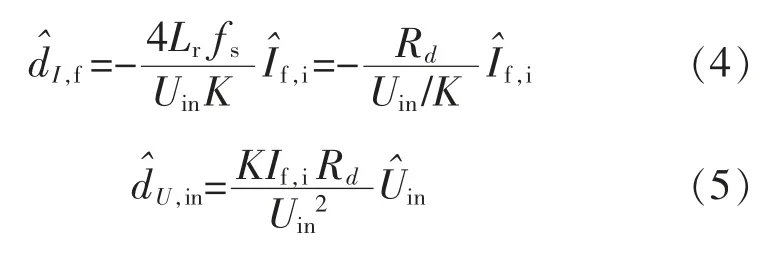

其中
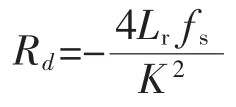
式中:fs为开关频率。将代替图3(d)中的从而可得PSFB 小信号模型,如图5 所示。
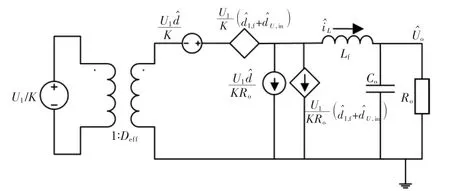
图5 移相全桥小信号模型Fig.5 Small signal model of PSFB

2 数字控制系统的设计
在此所设计的电路参数见表1。
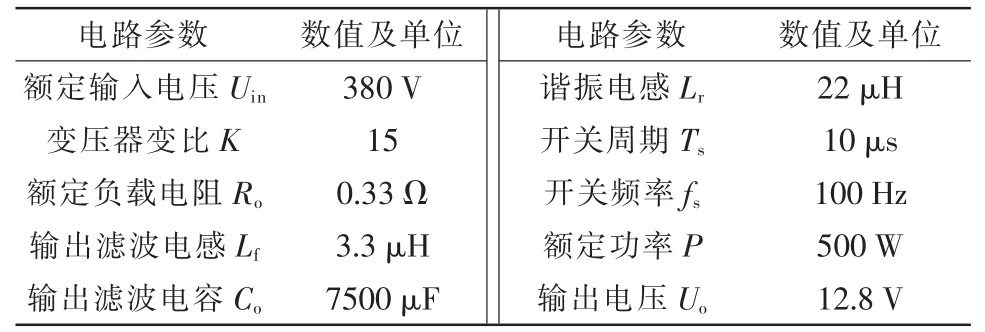
表1 设计电路的参数Tab.1 Parameters of design circuit
将表1 数值代入式(7),可得
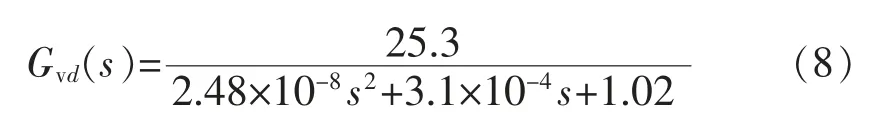
再对其进行伯德图分析,其过零频率为5 kHz,满足远小于开关频率的条件;相位裕量约为22°,幅值裕量大于50 dB。 在未增加控制的情况下,开环系统处于稳定状态,但带宽较小,响应速度较慢。 故应增加控制器提高系统响应速度。
在此,采用增量式数字PID 的方式进行调节,选用高速DSP 芯片作为主控单元, 在PSFB 电气回路的基础上增加输入电压电流、输出电压电流思路采样电路,电气量经过滤波后送入主控芯片AD 接口,在芯片内通过软件滤波,阈值保护后进行PID计算得到占空比,将的占空比进行PWM 变换与隔离后用来驱动开关管。 同时,利用芯片控制器局域网络CAN 接口进行整车通讯,如图6 所示。
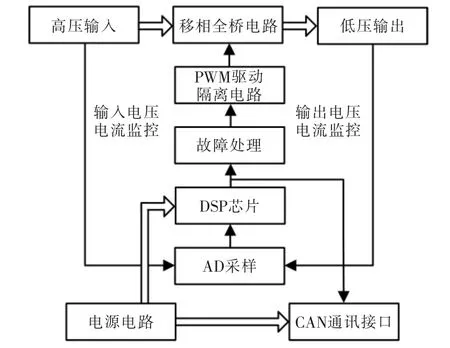
图6 数字系统设计Fig.6 Digital system design
软件控制部分分为主函数和中断函数部分,如图7 所示。 系统上电后自动开始开机检测,随后进入主函数循环,在主函数中主要进行阈值判断与保护。同时,设置定时中断函数,分为AD 采样中断、PID 计算中断、CAN 通讯中断。三者按任务的重要性划分优先级:AD 采样中断>PID 计算中断>CAN 通讯中断。
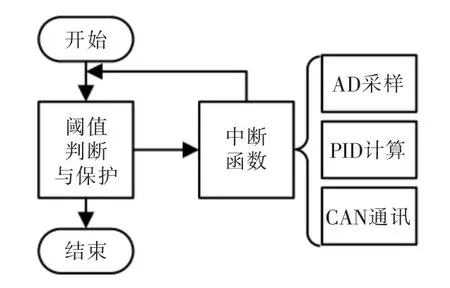
图7 软件流程Fig.7 Software flow chart
其中,PID 计算部分根据AD 采样得到的输出电压uo,ad与给定值相比较, 得到误差信号error,根据离散增量式PID 公式得到的占空比信号d 为
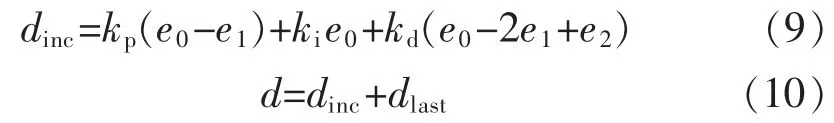
式中:dinc为占空比增量;d 为实时占空比;e0为当前误差;e1为上一次误差;e2为上两次误差;kp,ki,kd分别为增量式PID 参数。
3 Saber-Simulink 联合仿真
Saber 仿真软件在提供海量器件模型的基础上,允许用户自行建模,设计满足特定参数的器件,能很好地拟合实际情况,然而在数字系统方面有所欠缺,无法提供软件方面的仿真,不能进行功能性的算法设计。相反地,Simulink 是很强的控制系统设计工具,其S 函数功能能够提供C/C++等语言环境进行算法设计或改进,较好地符合实际情况中数字系统的设计环境,但在具体器件仿真方面不如Saber精准和方便。因此,采用Saber 作为硬件器件仿真工具,Simulink 仿真数字控制部分的联合仿真是最终选择。 联合仿真结构如图8 所示。
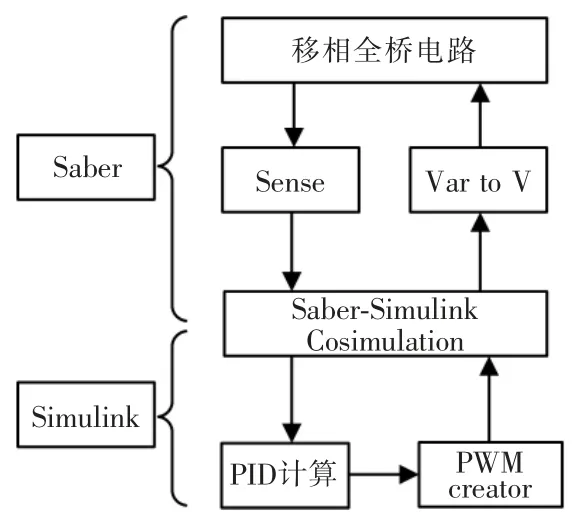
图8 联合仿真结构Fig.8 Joint simulation structure diagram
图中,在Saber 环境下搭建PSFB 的电气回路部分,并在其中加入Sense 与Var to V 模块,Sense 模块将电气参数转换为标量供Simulink 使用,Var toV模块接受来自Simulink 的控制信号用于驱动开关管。 Saber-Simulink Cosimulation 是Saber 提供的联合仿真接口,设置好采样步长后用于Saber-Simulink两者间的数据交互。
在Simulink 环境下则设计了2 个S 函数模块:PID模块与PWM creator 模块。PID 模块接受来自Saber的采样数据进行PID 计算后得到目标占空比,PWM creator 模块则根据计算得到占空比与斜坡信号比较,得到根据占空比调制的PWM 信号,该PWM 信号最终通过Cosimulation 模块返回Saber 软件中用于开关管的驱动。 Simulink 数字控制部分如图9。
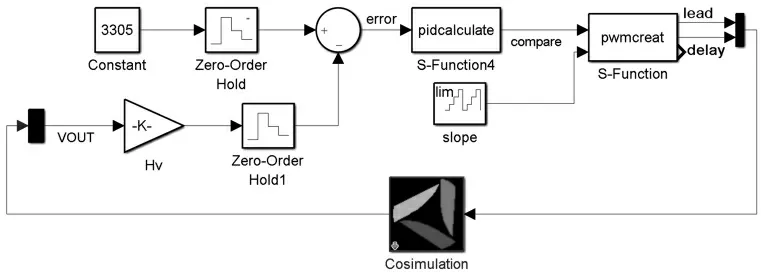
图9 Simulink 数字控制部分Fig.9 Simulink digital control part
其中,PWM 驱动信号的产生原理如下: 由斜坡模块产生最大值为1000,周期为10 μs 的斜坡信号slope。 将计算得到的占空比信号d 放大至0~400 得到比较信号compare,利用最大值为1000 的斜坡信号slope 与比较信号比较, 在比较信号等于斜坡信号时触发滞后臂信号delay 为高, 固定延时半周期(不考虑死区时间)后触发滞后臂信号为低;而超前臂信号lead 则在斜坡信号等于0 时触发为高,同样固定延时半周期(不考虑死区时间)后触发为低。 斜坡信号按规定周期循环往复,形成PWM 驱动信号,如图10 所示。
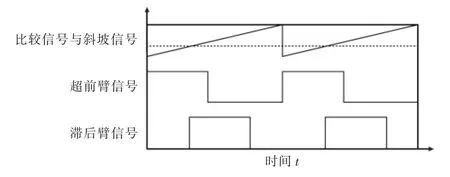
图10 PWM 调制示意图Fig.10 Schematic diagram of PWM modulation
根据输出电压超调不超过5%,尽可能减小响应时间的原则, 根据仿真结果调整PID 参数kp=0.01,ki=0.00005,kd=0.01。 得到仿真波形如图11 所示。 设计的仿真时长为0.3 s,半载启动,在0.2 s 时增加至额定负载。
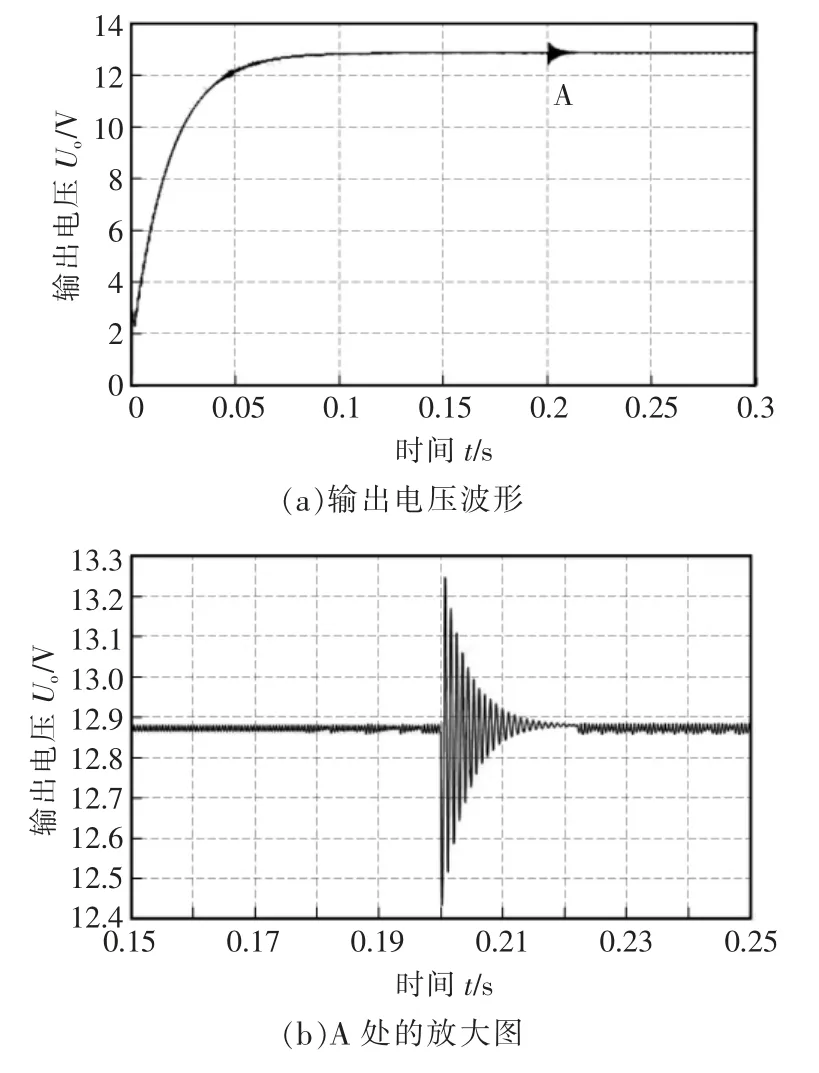
图11 联合仿真输出电压Fig.11 Joint simulation output voltage
图中,稳态情况下电压输出为12.8 V,电压纹波为0.04 V,调节时间为66 ms(按偏差2%计),0.2 s后负载增加至满载, 瞬时电压降落为0.4 V,20 ms 后重新进入稳态。
4 实践与归纳
在实验室环境下,设计基于NXP 公司56F84763DSP为主控芯片的PSFB 数控系统,其电气参数如下:
额定输入电压DC 380 V;
额定输出电压DC 12.8 V;
额定功率500 W;开关频率100 kHz。
进行样机试验,得到的输出电压如图12 所示。
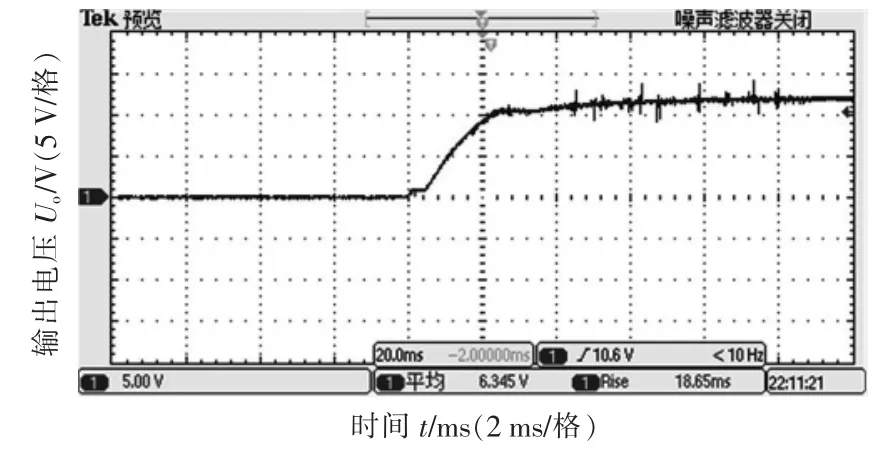
图12 样机输出电压Fig.12 Sample output voltage
图中,尖峰毛刺为开关噪声引起,关于高频噪声的抑制在此不做讨论。 其调节时间为40 ms,稳态电压12.5 V,电压纹波0.2 V(稳态值的1.6%),无超调现象。 可以看出,除尖峰毛刺外响应速度迅速、无误差,具有很好的快速性。
5 结语
通过对PSFB 拓扑进行分析与建模有助于了解开环系统的特性,有针对地进行数字控制系统的设计,在此基础上利用Saber 与Simulink 的各自优势,分别对硬件电路和数字控制部分进行仿真,有效地减小了PID 参数调整的时间,最终通过仿真结果与样机试验验证了分析的正确性。
