飞机大翼漆层打磨设备的混合控制策略研究
2019-05-09祝世兴王璐琦
祝世兴,刘 洋,王璐琦
(中国民航大学 航空工程学院,天津300300)
随着我国航空装备制造与维修技术业的不断发展,飞机维修市场对飞机大翼漆层打磨加工的需求不断提高。 然而,目前我国飞机大翼打磨抛光加工主要以人工为主,人工打磨效率低下,费时费力,精度不高,而且产品均一性差,工人的工作环境恶劣,难以实现自动化生产,延长了飞机大修停厂时间, 对飞机维修企业的经济效益产生不利影响,已经成为飞机维修行业进一步发展的瓶颈。 为此,飞机大翼漆层打磨设备的研究引起了行业内高校、科研机构和企业的广泛关注[1]。
使用飞机大翼漆层打磨设备能够实现高效率、高质量的自动化打磨,为替代当下人工作业提供了新的解决方案和技术突破[2]。 飞机大翼漆层打磨设备进行打磨时需要同时控制加工轨迹、产品末端的力,这种多环、连续、混合控制的实现难度很大。 飞机大翼漆层打磨设备的核心为打磨力控制技术,通过控制加工轨迹和打磨工具末端的力来保证打磨质量,即对打磨设备的位置和力两方面都要进行控制[3-5]。在此提出一种飞机大翼漆层打磨设备力/位控制方法,根据打磨轨迹规划坐标信息及打磨工具姿态。 通过三轴力传感器进行接触力的实时检测反馈,通过力和位置的函数关系,得到打磨点的法向偏置位移量,实时修正打磨轨迹,使末端快速逼近期望的打磨力,控制效率及作业质量较优[6]。
1 飞机大翼漆层打磨设备结构及工作原理
1.1 打磨力的测量与系统数学模型的建立
在整个作业系统中,飞机大翼漆层打磨设备本体末端通过机械装置与三轴力传感器相固联,如图1 所示。

图1 打磨头的受力分析Fig.1 Force analysis of grinding head
由图1 打磨头的受力分析可知

式中:Fg为打磨头与气缸顶杆间安装的力传感器的测量值;Fs为打磨头与飞机大翼面的接触打磨力;G为打磨头自身质量;θ 为打磨力方向与铅垂方向的夹角;F0为打磨头惯性力。 在实际加工过程中,Fg并不是单一的Fs,还包括G 和打磨头惯性力F0,所以需要进行重力补偿。
在飞机大翼漆层打磨设备进行连续运动时,由于打磨头质量G 并不大,且末端加速度很小,打磨工具惯性力F0可忽略不计。 即式(1)可简化为

假设气体流动为等熵流动过程,根据流进气缸下腔气体质量流量等于气体压缩流量与活塞运动所需流量之和,建立的活塞气缸气体连续性方程为

式中:q 为活塞下腔气体质量流量,kg/s;V 为活塞下腔容积,m3;R 为气体常数;k 为比热比,理想气体k=1.4;T 为下腔气体温度,K;p 为下腔气体压力,Pa;A为气缸活塞的有效面积,m2;y 为活塞气缸的位移,m。 气缸压力与负载的力平衡方程为
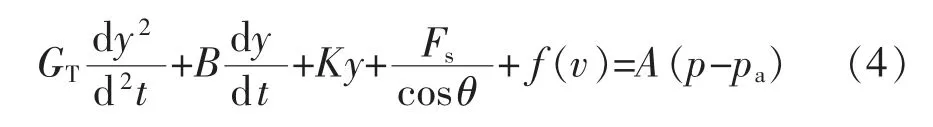
式中:GT为气缸质量负载,kg;B 为黏性摩擦系数,N·s/m;K 为负载弹簧的刚度,N/m;f(v)为活塞与气缸壁的摩擦阻力,N;pa为大气压力,Pa。 偏差电流信号Ie为

式中:Ir为指令电流信号;If为反馈电流信号。 力传感器方程为

式中:KfF为力传感器增益;Fg为气缸输出力。PID 控制器输出为
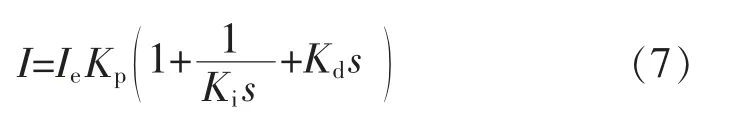
电气比例阀输出压力为
式中:Kv为电气比例阀增益。 由式(3)和式(4),可得气缸输入压力p 至打磨输出力Fs的传递函数为

该设备控制系统的原理如图2 所示, 根据式(6),式(8)和式(9),可绘制传递函数方框图(如图3所示),由此得到系统的开环传递函数为


图2 控制原理框图Fig.2 Control principle block diagram

图3 传递函数框图Fig.3 Transfer function block diagram
1.2 飞机大翼漆层打磨设备主体结构
打磨设备机械主体结构如图4 所示。 飞机大翼漆层打磨设备机械系统由“两纵一横”二维十字滑台、万向节、打磨工具等组成。 控制系统主要分为2部分:①由力传感器、电气比例阀及气动恒压活塞控制机构来实现对打磨力的控制; ②由步进电机、步进驱动器、PLC、电机旋转编码器及限位开关等来完成对打磨位置的控制。

图4 打磨设备机械主体结构Fig.4 Mechanical main structure of grinding equipment
力传感器安装在打磨工具与万向节之间,测量在传感器坐标系打磨工具和大翼漆层之间的打磨正压力的大小, 再将测量的信息反馈给力控制器,力控制器对电气比例阀输出压力进行调节,气动恒压活塞控制机构进行相应动作以保持打磨工具和加工件之间的力相对恒定,从而保证打磨的效果。
路径规划程序内置于PLC 用来对打磨工具在大翼上的打磨路径进行规划,工作时并将实时的打磨工具位置信息传递给控制器,控制器驱动打磨机到达相应位置开始打磨。
2 仿真物理模型的建立
利用MatLab/Simulink 平台Simspace 物理模型[7-11],建立对基于打磨力控制的飞机大翼漆层打磨设备控制系统物理模型,然后通过仿真分析验证该打磨设备控制系统的可行性。
由于Simscape 可以提供一个自然、高效方法来构建物理系统的数学模型。 通过物理连接系统模拟各元件间的机械及气动关系[11],在此基础上可以直接引入Simulink 控制模块实现对机械系统的完整仿真,由此得到控制方案的效果,并对控制参数进行优化。
建立的打磨压力控制系统Simspace 模型如图5所示。 其中,Preumatic Piston Chamber 为单活塞腔A 为压力信号输入端口,H 为温度输入端口;Ideal Force Sersor 为测定活塞杆输出压力的传感器组件;Ideal Transltional Motion Sersor 为测定活塞位移和速度的传感器组件。

图5 仿真物理模型Fig.5 Simulation physical model
按照物理系统机械结构的实际设计参数设置该仿真模型的各个参数:
GT=Mass=5 kg,K=8.8×102N/m,B=10 N·s/m,Kp=8,Ki=0.5,Kd=0.6。
3 仿真结果分析与优化
重力补偿后,经过仿真运算得出打磨力输出特性曲线、 活塞位移特性曲线和活塞速度特性曲线(如图6—图8 所示)。
图6 为未经优化的打磨力响应曲线。 其最大超调量为56%,经过1.5 s 达到稳态。 因最大超调量过大,为控制极限打磨力为不超过对大翼造成损伤的25 N,将使稳态工作打磨力较额定打磨力低4 N。 因其不满足设计控制要求,需进一步优化。

图6 (优化前)打磨力输出特性曲线Fig.6 Output characteristic curve of grinding force(before optimization)

图7 活塞速度特性曲线Fig.7 Piston speed characteristic curve

图8 活塞位移特性曲线Fig.8 Piston displacement characteristic curve
经过优化的打磨力响应曲线如图9 所示。 其最大超调量为15%稳态打磨力为20 N, 经过0.7 s 达到稳态。 稳态工作打磨力为设计额定打磨力20 N,可以满足控制系统设计要求。
4 结语

图9 优化后的打磨力输出特性曲线Fig.9 Output characteristic curve of grinding force after optimization
在飞机大翼打磨设备机械结构的基础上,提出了一套与之相匹配的打磨力与打磨轨迹控制系统。针对其中的重难点打磨力的控制, 利用MatLab/Simulink 平台建立了Simspace 物理模型,将建立的物理模型与Simulink 控制信号调节元件联合仿真。仿真结果表明,通过PID 控制器优化后,其输出特性曲线最大超调量和响应时间均在设计要求范围内,对打磨压力的调节满足飞机大翼打磨力的控制要求。
