基于EMD 的滚动轴承故障诊断方法研究

2019-05-09陶栩

自动化与仪表 2019年4期

陶栩

（四川中烟工业有限责任公司，成都610017）

滚动轴承寿命离散性很大，无法通过设计寿命预估其故障频次、故障点[1]。对滚动轴承故障，运用科学、智能的方法进行检测，一直是机械设备各自动化诊断故障的重要研究点之一。使用先进的技术方法，及时、精准、高效地监控滚动轴承的运行状态，利用故障诊断技术进行故障特征的分析与判断，以便掌控轴承运行过程中的性能状态，及时发现潜在隐患，优化设备运行水平，增加企业效益。为此研究了新的故障诊断方法，判别轴承在运行中存在的故障隐患，提高设备的维修管理水平及运行效率。

1 滚动轴承的振动

在工业生产实际中，滚动轴承的外侧圈一般与轴承的底座或者外壳直接连接，多采用固定或者相对固定的方式进行连接。由于轴承的结构特点，固定中的安装失误、运行过程中受力不均衡，以及其他突发故障等都会使包括轴承在内的整体系统发生较为强烈的振动，引起谐振，其成分包含低频故障特征频率和高频固有振动频率[2]。固有振动频率范围集中在（1～50）kHz，而轴承的故障特征频率多小于1 kHz。因此通过分析谐振频率信号，可以对轴承损坏情况及故障发生的部位进行诊断[3]，内圈故障频率fi和外圈故障频率fo分别为

式中：D 为轴承节径；d 为滚动体直径；Z 为滚动体个数；α 为接触角；fr为转动频率。

2 基于EMD 诊断方法

滚动轴承在运行中产生的振动信号成分丰富，包含多种频段故障信号，因此其故障特征在不同频带上都有所反映。经过经验模态分解后，得到的各阶IMF 分量通常都会包含因故障引起的不同振动成分[4]。结合峭度系数，选择峭度大于3 的IMF 分量重新构造诊断信号，并对该信号运用Hilbert 法进行解调，然后通过频谱分析解调出的包络信号，由此得到轴承振动信号中所包含的各故障特征的精准信息[3]，辅助判断存在的故障。

2.1 EMD

经验模态分解（EMD）是依据信号自身的时间尺度特征对信号进行分解[5]，其目的在于将性能不好的信号分解为一组性能较好的本征模函数[6]，即

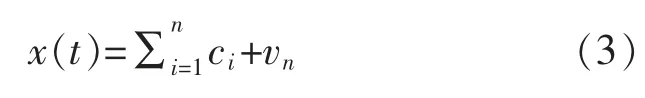
2.2 峭度系数

峭度系数是无量纲参数，它与轴承转速、尺寸、载荷等无关，对冲击信号敏感，特别适用于表面损伤类故障，故以峭度作为故障诊断特征量是行之有效的[7]。峭度系数K 定义为

式中：N 为信号长度；μ 为信号x 的均值；σ 为信号x的标准差。

2.3 Hilbert 包络分析

Hilbert 变换可以将时域信号转变成一种解析信号，在求取瞬时频率和瞬时幅值方面起着重要作用。对任一个时间序列x（t），其Hilbert 变换为

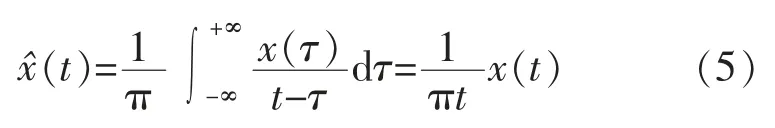
x（t）的解析信号z（t）为

如果x（t）受到振幅调制，则

2.4 傅里叶变换

频域分析就是将以时间为横坐标的时域信号，通过傅里叶变换，将信号转化为以频率为横坐标的频域信号[8]。在得到频域信号以后，先通过分析频谱图中的频率成分，再比对各种频率成分的幅值大小，由此诊断滚动轴承[9]。其数学运算式为

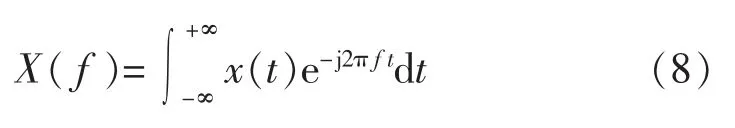
式中：X（f）为信号的频域表示；x（t）为时域信号。

3 实例分析

在此选用驱动端轴承为SKF 深沟球轴承，采样频率为12 kHz，电机负载为1.5 kW，电机转速为1750 r/min，故障点直径0.1778 mm[10]。轴承标准参数如下：轴承节径为40 mm；滚珠直径为8 mm；滚珠9个；接触角为0°。

根据基本参数，按照式（1）和式（2）计算出轴承内圈、外圈的理论故障特征频率分别为157.5 Hz 和105 Hz。滚动轴承内外圈发生故障的时频图如图1所示。

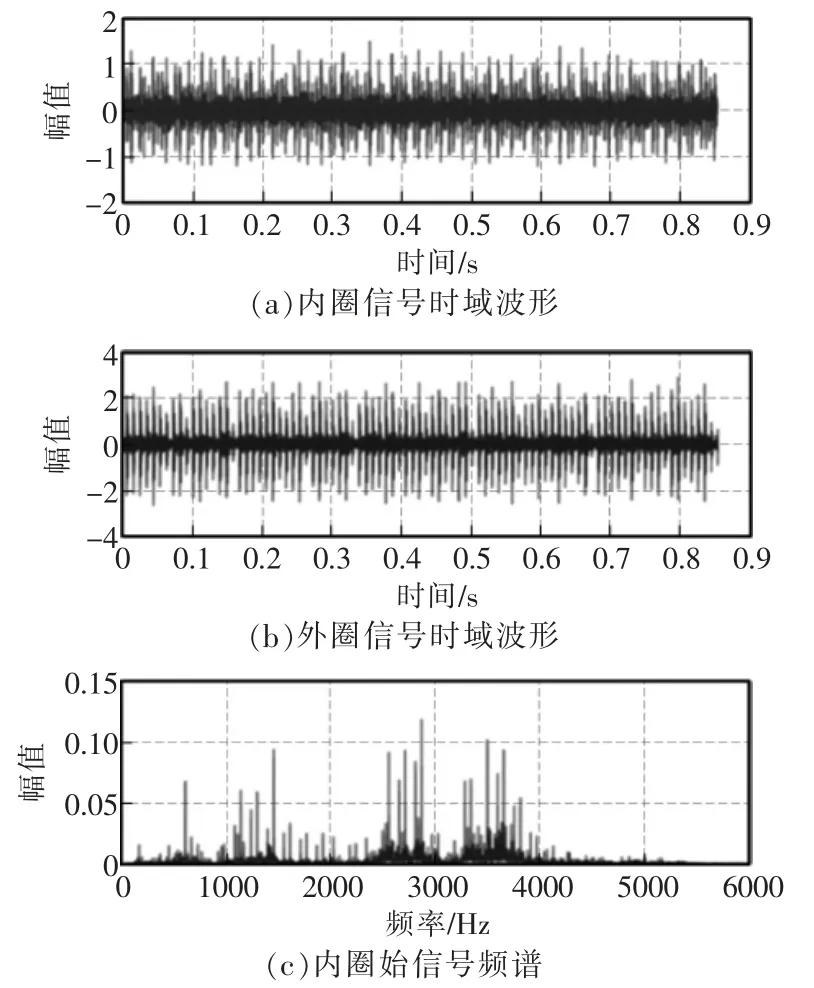
图1 内外圈时频图Fig.1 Time frequency diagram of inner and outer rings

由图1（a）（b）可见，原始故障信号在时域内波形非常复杂，含有丰富的频谱分量，所以未能突显出故障的特征频率。将原始信号进行EMD 分解，采样点数10240。分解后，由轴承内圈的故障信号得到12 阶的IMF 分量和其他残余分量；外圈信号得到14 阶IMF 分量和残余分量，具体见表1 和表2。

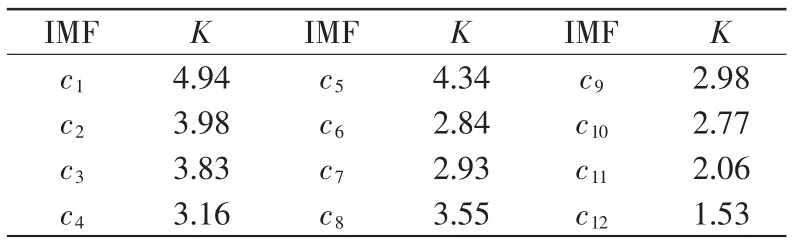
表1 内圈各阶IMF 峭度值Tab.1 IMF kurtosis values of the inner ring

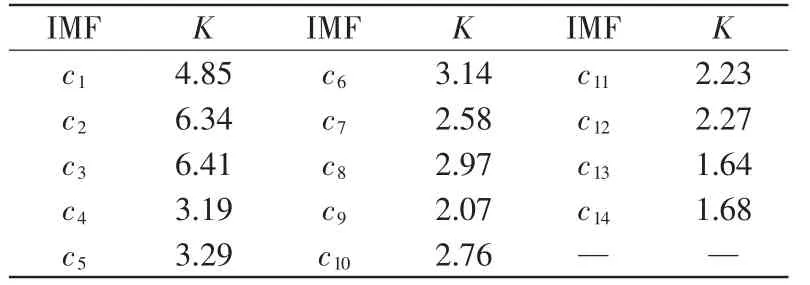
表2 外圈各阶IMF 峭度值Tab.2 IMF kurtosis values of the outer ring

由表1 数据可知，滚动轴承内圈的第3，5，8 阶IMF 分量的峭度值都非常大。由表2 可知，轴承外圈的前五阶IMF 分量具有较大的峭度值；同时与其它的IMF 分量相比，它们包含有更多的故障信息。内圈、外圈原信号和所选取的IMF 分量如图2 所示。

将选取的各阶IMF 分量进行叠加，得到重构信号IMFre，然后对IMFre 进行Hilbert 变换，随后运用傅里叶变化进行频谱分析，得到内外圈包络谱，如图3 所示。

由图3（a）可以看到，第1 个频率为157.5 Hz 的谱峰，第2 个频率为314.9 Hz 的谱峰，第3 个频率为472.4 Hz 的谱峰，第4 个频率为786.6 Hz 的谱峰。通过将这4 个谱峰值与SKF 深沟球轴承的故障特征频率相比较，可以发现其分别与特征频率157.5 Hz，与特征频率的2 倍频315 Hz，3 倍频472.5 Hz，以及5 倍频787.5 Hz，都十分接近。

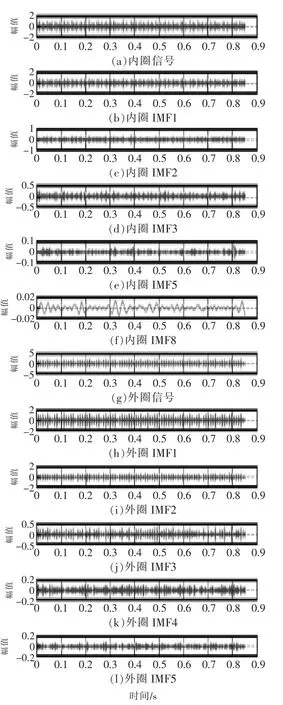
图2 故障信号及所选取的IMF 分量的时域波形Fig.2 Time domain waveform of the fault signal and the selected IMF component

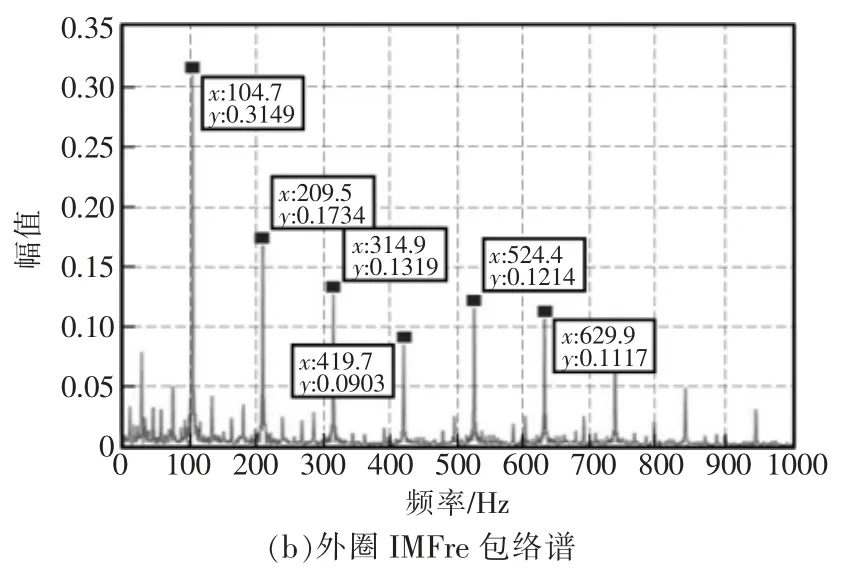
图3 重构信号IMFre 包络谱Fig.3 Reconstructed signal IMFre envelope spectrum

同样，由图3（b）外圈重构信号的包络谱，可以看到频率分别为104.7，209.5，314.9，419.7，524.4，629.9 Hz 的6 个不同谱峰。同时，计算出的频率值与特征频率105 Hz，与特征频率的2 倍频210 Hz，3 倍频315 Hz，4 倍频420 Hz，5 倍频525 Hz，6 倍频630 Hz也都十分接近。

由此可以判断，该滚动轴承内圈和外圈发生了故障，该判断结果也与实际情况相符。