地铁健康监测PCBN模型的参数相关性分析

2019-05-09刘文黎吴贤国张文静王彦玉

土木与环境工程学报 2019年2期

刘文黎，吴贤国，张文静，王彦玉

(华中科技大学土木工程与力学学院，武汉 430074)

随着地铁运营网络规模的逐年扩大，盾构地铁结构运营安全问题逐渐凸显，为了对盾构地铁结构的安全状态进行准确评估，许多研究者进行了大量的工作，提出了许多方法，包括模糊层次分析法[1]、事故树分析法[2]、模糊综合评价法[3]、可靠度评价法[4]等。但是，盾构地铁赋存环境因素对地铁承载性能的影响有着复杂的非线性、随机性、不确定性及多时空演化等特征。传统的评估方法多局限于静态的推理过程，难以构建监测指标与结构安全之间的隐性非线性映射关系，进行实时风险评定、动态风险预测以及风险诊断推理。

贝叶斯网络(Bayesian Networks，BN)能够直观地构建两个或多个随机变量因素之间的条件概率分布，且能够将先验信息与样本数据有机结合，实现网络节点因素之间的实时推理[5]。传统的贝叶斯网络较适用于分析离散的节点变量，且难以实现网络节点的动态评价，目前的混合贝叶斯网络、动态贝叶斯网络能较好地解决连续节点变量及节点动态概率评估问题，但对节点相关性的描述中存在Gaussian相关性的假设，难以构建节点之间的非正态相关性结构关系[6]。Copula理论能较好地捕捉参数之间的非线性相关性，构建两个或多个随机变量联合分布函数，进行参数相依性建模[7]。Pair-Copula是在Copula理论基础上发展出来的一种高维相依性建模的方法，藤结构为高维Copula提供了可行、有效的建模方式。但在实际应用中，高维下的参数估计较复杂，且可能会出现“过拟合”现象，藤结构无法解释变量间连接关系的实际意义，不利于实际工程中因素之间的逻辑推理[7]。

Kurowicka等[6]将Pair-Copula的概念应用到贝叶斯网络当中，得到一种新型的Pair-Copula构建方式，该模型被定义为PCBN模型。本文基于PCBN模型理论，首先，给出基于PCBN模型的盾构地铁运营安全评估模型设计方法，通过对单节点边缘分布拟合优度检验、选取多节点联合分布中的最优Copula函数；然后，采用能够高效捕捉多元参数之间相关性关系的Pair-Copula模型，结合贝叶斯网络理论，完成参数相依性的准确识别和高精度重构；最后，利用PCBN模型进行武汉三号线某空推段进行节点相关性分析，进而进行安全状态可靠度相依性推理，为盾构地铁结构的安全控制和风险管理提供一条全新的思路。

1 Pair-Copula贝叶斯网络模型

1.1 Pair-Copula理论

设函数f(x1,x2,…,xn)是n维随机变量X= (X1,X2,...,Xn)的联合分布密度函数，则函数f(x1,x2,…,xn)可以分解成

(1)

则多元联合分布的密度函数可以用一系列Pair-Copula密度函数和边缘条件概率密度函数的乘积来构建。

(2)

式(2)中，v=(v1,…,vj,…,vd)，是一个d维向量，vj是其中任意一个向量，1≤j≤d，而v-j=(v1,…,vj-1,vj+1,…,vd)表示在v中去掉vj，用密度函数式(2)还原分布函数，其中，Cuvj|v-j是一个二元Copula函数，则有

(3)

根据Vine-Coupla理论，有两种常见的藤Copula分解模式。

1)C-Vine。在C-Vine的结构中，对任意一棵树Tj，都有且仅有一个点连接到其他n-j条边上。这意味着，如果资产组合中存在一个能影响其他标的的资产，那么这个组合比较适合用C-Vine结构来构建。 Bedford等[8]给出了C-Vine结构的n维变量联合分布的密度函数表达式。

(4)

2)D-Vine。D-Vine的结构中每棵树的任何一个节点最多只连接的2条边缘。这意味着，如果一个资产组合中成分标的资产都相对独立，那么这个资产组合比较适合用D-Vine结构来构建。Bedford等[8]也给出了D-Vine结构的n维变量联合分布的密度函数表达式。

(5)

1.2 贝叶斯网络

贝叶斯网络通常表示为BN=(G,P)，其中，G=(V,E)为DAG，相应的结点集合和有向边集分别为V和E，P为每个节点的条件概率表，用以定量描述父结点对该结点的作用效果(Conditional Probability Table, CFT)。对于贝叶斯网络中任意随机变量X= (xt1,xt2,…,xtn)，相应的联合概率分布可以表示为[5]

(6)

式中:T为时期长度。如果随机变量X为时间序列，且xti的父结点为(xtj-1,…,xt1)。根据概率论中的链规则，即联合概率可以由其条件概率链表达，公式(6)右端项的条件概率函数构建如

(7)

1.3 Pair-Copula贝叶斯网络模型(PCBN)构建

令D= (V,E)表示一个BN对应的DAG，V为顶点集，E为边集，用Dm表示D的道德图。令P表示Rd上绝对连续的概率测度，其中d=|V|，令X为概率分布为P的随机变量，假设P的概率密度函数为f，若P满足D-马尔科夫属性，通过Sklar定理，可知P的概率密度分布函数(CDF)能被唯一分解成一系列单变量边际分布F1,F2,…,Fd和一个Copula函数C的乘积。Bauer等[7]证明Copula函数C能被进一步分解成一系列(条件)Pair-Copula函数Cυ，ω|pa(υ)，其中υ∈V，ω∈pa(υ)，贝叶斯网络为Copula提供了一种新型的PCC模型，其中每个(条件)Pair-Copula对应网络结构D中的一条边ω→υ，将节点与其母节点相连接。因此，P的概率密度函数f最终被分解为：

(8)

式中：x=(xυ)υ∈V∈Rd，该模型被称为PCBN模型。

2 结构失效模式及可靠度理论

2.1 运营盾构地铁结构失效模式确定

1)纵向螺栓受剪破坏模式。受到外荷载的影响，相邻的两片管片之间可能会出现相互位移，即产生径向错台值(V11)。如果相对位移量过大，纵向螺栓可能因为剪力过大而破坏，相对弯曲的竖向位移由纵向螺栓的最大位移值确定，而水平距离为两环盾构管片的宽度，若螺栓受剪破坏时其极限的竖向位移为ωmax(即径向错台值)，则管片受剪时的相对弯曲[9]为

(9)

式中：l为纵向螺栓有效长度的一半；[τ]为纵向螺栓抗剪强度；A为单根纵向螺栓的横截面积；EI为单根螺栓的抗弯刚度；L为一环盾构管片的宽度。纵向螺栓受剪破坏的失效函数为

g1=ωa-ωmax

(10)

式中：ωa为在外荷载作用下的径向错台量(V11)。

2)纵向螺栓受弯破坏模式。盾构地铁结构通常采用装配式结构，在弯矩作用下，盾片环以中性轴为界，受压一侧管片混凝土被压缩，受拉一侧的管片和纵向螺栓均受拉，地铁轴线产生一定的弯曲曲率，而盾构地铁结构的主要破坏形式为外侧受拉的纵向螺栓受拉屈服。当盾片处于受弯变形模式时，外侧的受拉螺栓处于高危状态，借鉴Huang等[10]对盾片受弯、受力模式的分析及Hooke’s定理可得，管片结构的安全性由螺栓的抗拉强度控制，则盾构地铁的最大纵向曲率半径为

(11)

式中：E为螺栓的杨氏弹性模量；Dout为盾构环的外径；l为盾构管片的厚度；L为连接螺栓的长；ρmax为最大纵向曲率半径；[σ]为螺栓抗拉强度值。纵向螺栓受弯破坏的失效函数为

g2=ρa-ρmax

(12)

式中：ρa为在外荷载作用下的纵向曲率半径(V9)。

3)横向螺栓受拉破坏模式。Huang等[4]提出通过横断面水平收敛值判断t时刻的盾构管片变形性能Q(t)。

(13)

式中：ΔD(t)为t时刻的盾构管片累积水平收敛值；ΔDF为盾构管片的极限水平收敛值；Dout为一环盾片的外径。根据Liu等[11]研究成果，考虑到在实际盾构地铁工程中，由于受外荷载等不确定因素的影响，断面的极限收敛值并不一定出现在水平向，故而选取全断面的极限收敛率ΔDmax/Dout=0.030 3为盾构截面承载力极限值。横向螺栓受拉破坏的失效函数为

g3=ΔDa-ΔDmax

(14)

式中：ΔDa为在外荷载作用下的断面收敛值(V10)。

2.2 基于可靠度理论的盾构地铁运营安全控制体系构建

确定盾构地铁结构的风险状态水平，有助于对运营盾构地铁结构的安全进行管控。本文将系统的失效概率作为判断建筑风险状态的基础，为研究盾构地铁结构的安全可靠性，采用蒙特卡洛模拟法确定系统的失效概率，计算公式为

pf=P[g1(CD)<0∪g2(SD)<0]

(15)

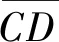
β=Φ-1(1-pf)

(16)

式中：Φ-1(·)为指标准正态分布函数的反函数。

3 工程实例分析

3.1 工程概况

选取武汉市轨道交通三号线工程自跨江段右线王宗区间地铁部分空推段，监测区间为自跨江段右线王宗区间设计起点里程右DK9+696.728起，向宗关方向延伸320 m左右，覆盖了王家湾站附近的部分商业区下的地铁区间。该段地铁区间有一部分穿越汉江，地铁赋存环境中水压较大，部分区段出现渗透水病害，该区段地铁运营受到地铁运营管控部门的极大重视，故对该段地铁区间从距离右DK9+696.728点号15 m的环号开始布置的监测系统的100组监测数据进行分析。

采用自动化监测中的远程自动全站仪和应变、倾角传感器进行自动化监测数据，如图1，结合其他人工监测得到的数据，建立监测参数之间的PCBN模型，评价该段地铁区间的安全可靠性，为地铁的安全风险管理提供信息支持。

图1 各监测仪器布置示意图Fig.1 Schematic diagram of each monitoring

3.2 基于PCBN的运营安全评估

3.2.1 地铁运营安全PCBN模型结构设计 1)地铁运营安全PCBN模型网络节点设计。为对地铁运营安全PCBN模型网络进行节点设计，需建立表征盾构地铁结构安全性能的节点指标体系，考虑到指标敏感性程度、网络模型复杂程度、实际工程[2-3]，参考文献[12-15]和相关规范[16]，构建的PCBN模型节点包括：拱顶沉降值(V1)、水平收敛值(V2)、管片剥落面积(V3)、差异沉降值(V4)、裂缝面积(V5)、渗透水量(V6)、管片倾斜度变化量(V7)、接缝张开值(V8)、纵向曲率半径值(V9)、断面收敛值(V10)、径向错台值(V11)。2)网络结构DAG图设计。基于故障树理论，将节点之间相依关系的故障树转换为PCBN模型网络结构DAG图，结合相关工程经验和专家认知，初步对PCBN模型DAG图进行修剪和完善，构建的地铁运营安全PCBN网络DAG设计图如图 2所示。通过这种方式能够极大地提高PCBN模型网络结构DAG图构建的效率，同时，避免完全依靠数据驱动的网络结构DAG图学习可能出现的过拟合问题。

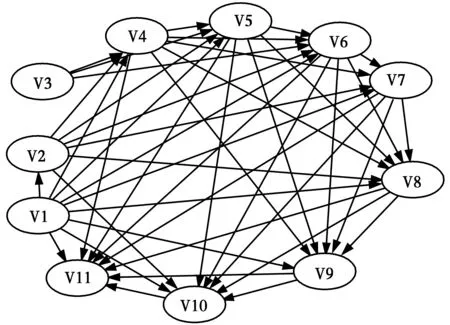
图2 地铁运营安全PCBN模型网络DAG设计图Fig.2 DAG design of the subway operation safety

3.2.2 地铁运营安全PCBN模型参数设计 1)节点间独立性检验。为精简构建的PCBN模型DAG图，基于监测数据，对图 2所示每一条存在有向连接线的两节点之间的独立性进行基于Kendall’τ(统计量T)和基于经验Copula的独立性检验(统计量Tn)，发现V1-V5、V1-V6、V2-V4、V4-V5、V4-V7、V4-V8、V5-V8、V5-V10、V5-V11、V6-V7、V6-V10、V6-V11、V7-V9、V8-V9之间相互独立，故在PCBN模型DAG图删除这些节点间的有向连线。

2)网络参数设计。利用Pair-Copula理论能够构建贝叶斯网络连接边之间的相依结构，本文利用AIC、BIC和DIC3种不同判断准则，识别4种Copula函数中最优Copula，构建的PCBN模型的29条边中，14条边的最优Copula函数为Frank Copula、11条边为Gumbel Copula、3条边Clayton Copula，而只有一条边的最优Copula函数是Gaussian Copula。这表明，由于参数之间的相关性不同，其最优Copula函数并不同，不应对参数之间相关性存在先验性的预设，说明了传统的贝叶斯网络模型的假设并不准确，也进一步验证了采用本文构建的PCBN模型的函数的合理性和精确性。

在PCBN模型DAG图删除如V1-V5等相互独立的节点间的有向连线，并计算各节点之间的相关系数所得结果如图 3所示。

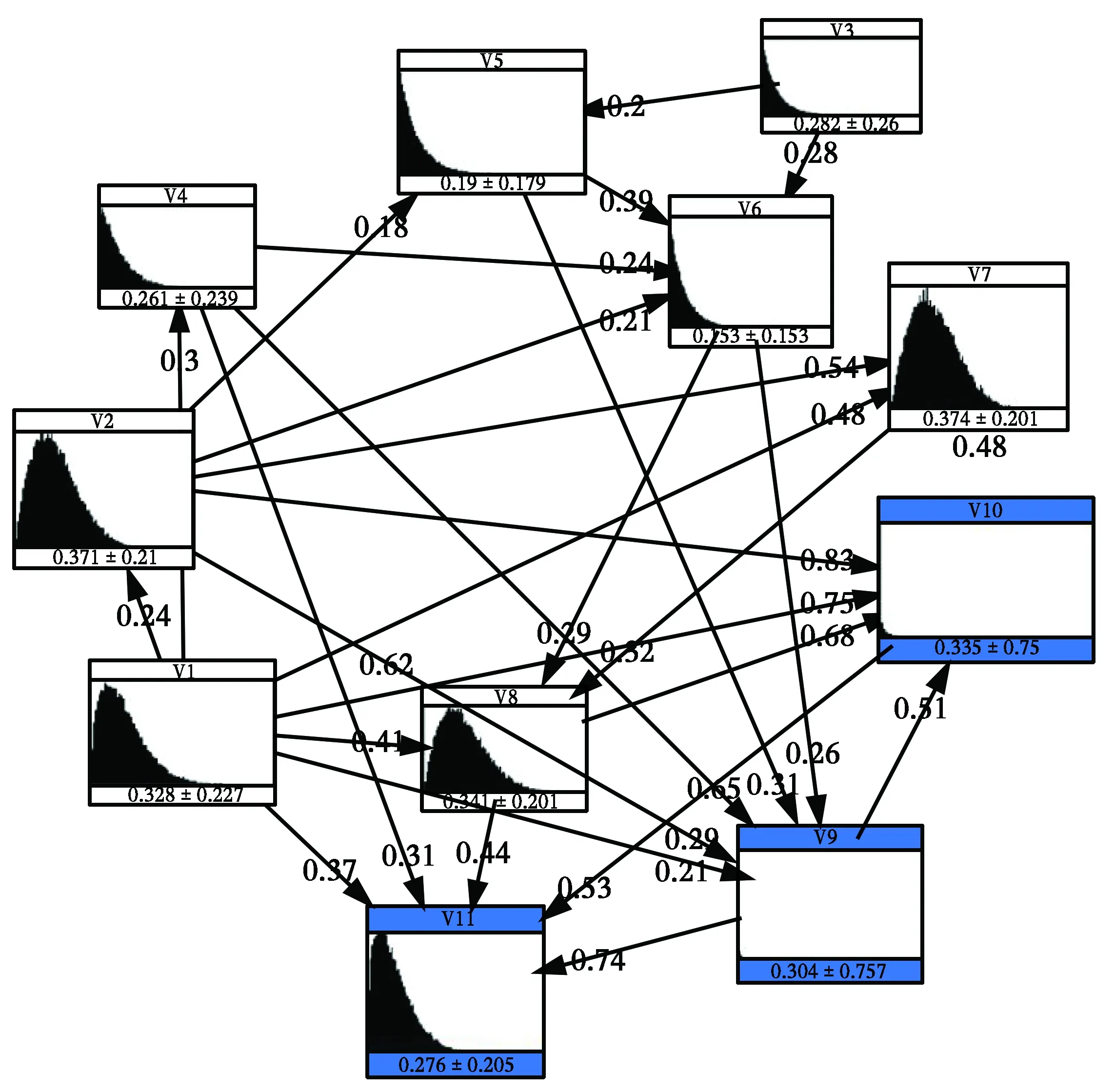
图3 PCBN模型网络节点相关系数Fig.3 PCBN model network node correlation

为了进一步验证PCBN模型的可靠性，对比模型生成V11节点(径向错台值)预测值的统计特征和健康监测得到实测值的统计特征，包括其均值、标准差、偏度和峰度，发现预测值与实测值的均值和标准差呈现近似一致的趋势，虽然预测值的偏度和峰度均低于实测值，但偏差不大。综合来看，预测值与实测值的均值、标准差、偏度和峰度均非常近似，表明所构建的PCBN模型能够较好地预测盾片错台值，进而验证了模型的准确性。

3.3 基于PCBN模型的节点相关性分析

3.3.1 参数联合分布散点图分析 1)V1节点与其他节点的散点分布研究。由于无法通过图像显示11维空间中的参数相关性，以V1节点与其他10个节点的散点分布为例，描述PCBN模型得到的节点之间相关性，得到V1节点与其他10个节点的散点分布以及拟合曲线，以V1和V2、V3为例，如图 4所示。

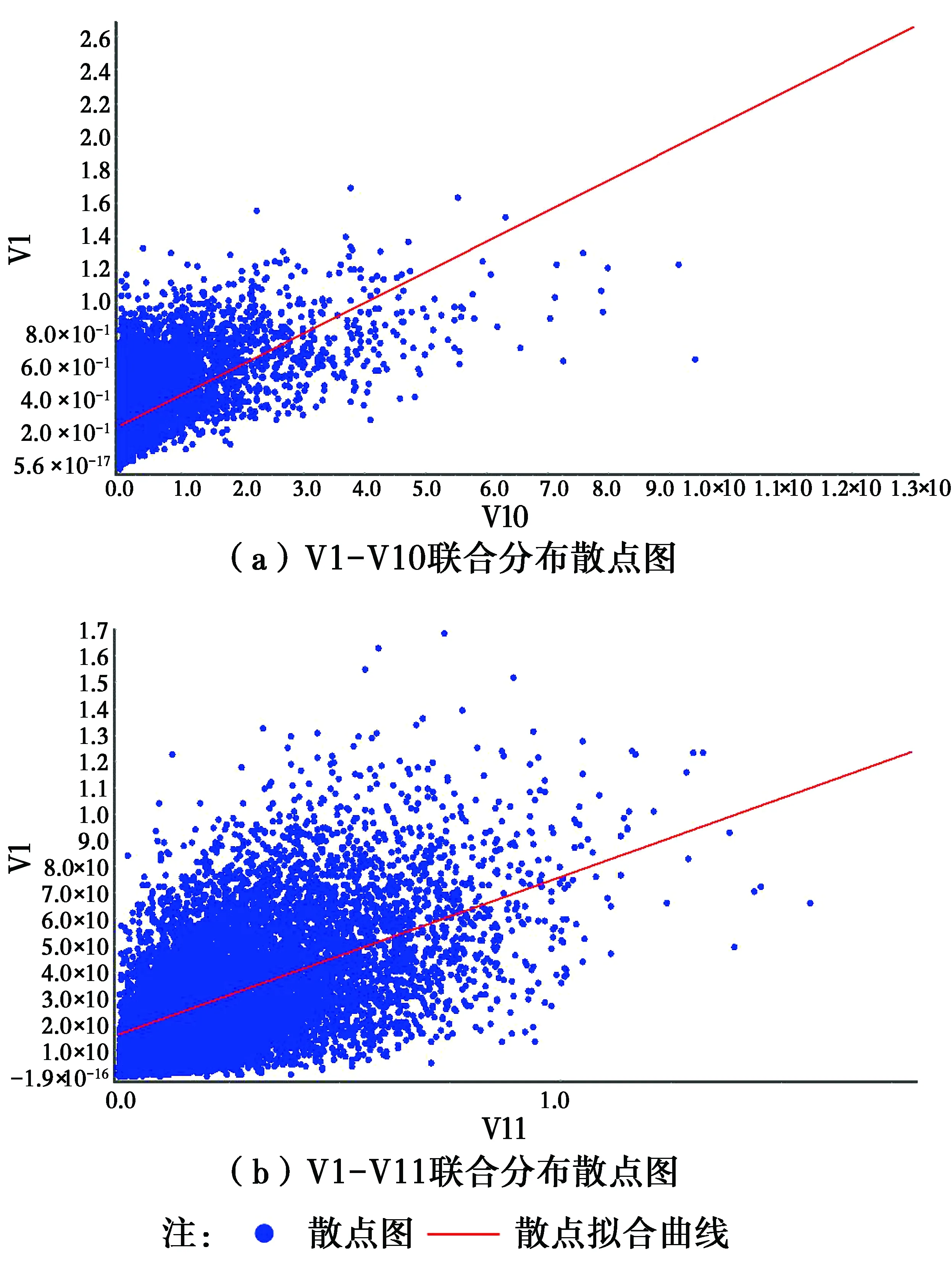
图4 V1节点与其他节点的联合散点分布及拟合曲线图Fig.4 Joint scatter distribution and fitting curve of V1 node and other

若参数的散点分布呈现斜45°角的分布规律，或者散点图拟合曲线的斜率越大，表明两参数之间的相关性越大。利用PCBN模型模拟得到的散点图的分布规律并不相同，其中，V1-V10的散点最为密集，呈现一定的斜45°角的分布规律，且其拟合曲线的斜率也最大，显示了V1节点与其他节点中，V1与V10节点的相关性最大；V1-V2、V1-V7、V1-V8和V1-V11的分布呈现明显的椭圆形的斜45°角分布，呈现较强的相关性；而V1-V3、V1-V5和V1-V6的拟合曲线的斜率趋近于0，呈现弱相关性。这些结论与利用原始监测数据得到的参数之间的相关关系较为吻合，表明PCBN模型能够很好地捕捉参数的相依性，并通过蒙特卡洛模拟法生成稳定的模拟数据，该数据能够用于后续的结构失效概率与可靠度分析。2)V9-V10-V11的三维联合散点图分析。在本文构建盾构地铁结构运营安全可靠性评价PCBN网络模型中，每一环盾片结构的状态由一个11维的状态空间数据进行描述，由于难以描述数据在高维空间的分布规律。V9、V10和V11作为本文评价盾构结构运营安全判定指标，以一环盾片的V9、V10和V11三维属性为例进行分析，100组V9、V10和V11监测值散点分布图如图5所示，而10 000组基于PCBN模型的V9、V10和V11模拟值散点图如图6所示。

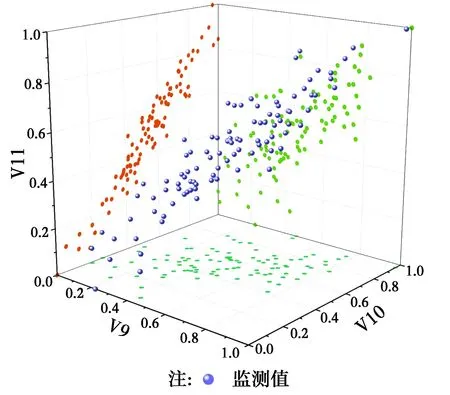
图5 原始V9、V10和V11监测值散点图Fig.5 scatter plot of the original V9, V10 and

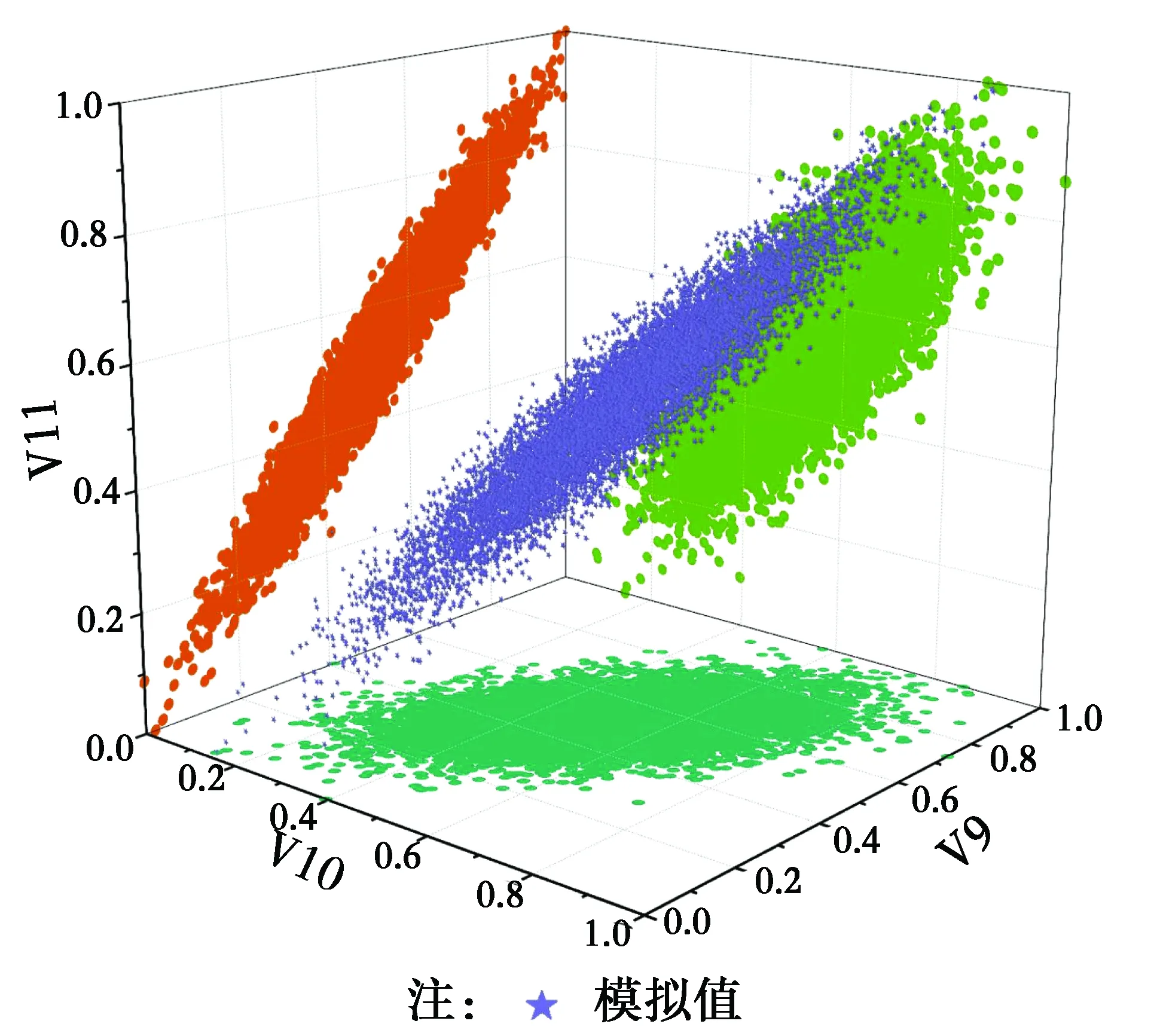
图6 基于PCBN模型的V9-V10-V11模拟值散点图Fig.6 V9-V10-V11 analog value scatter plot based

对比图5和图6可知，由V9、V10和V11的三维分布可知，原始监测值和模拟值散点的聚集状态比较类似，均是呈现束状分布。表明用PCBN模型生成的模拟数据与原始数据相似度较高，较之传统的贝叶斯网络模型，生成的数据保留了参数之间的相关性。图 5和图 6中的三维散点投影在各个二维面上，呈现了两个参数之间的相关性。对比V9-V10、V9-V11和V10-V11之间的相关性发现，V9-V11的相关性最强，其二维散点分布聚集的非常紧密，V10-V11次之，散点较为离散，V9-V10最弱，散点分布得非常离散。且对比图5和图6也能发现，PCBN模型能精准捕捉参数的相依性关系。通过Pair-Copula理论可以构建参数的相依性模型，能够更精确构建这些属性的在高维状态空间中的分布规律，同时，也表明该模型能够用于盾构地铁结构的安全可靠度精确评估。

3.3.2 节点参数的百分位蛛网图分析为使PCBN模型构建的联合分布模型的结果更加可视化，绘制了参数联合分布的百分位蛛网图(Percentile Cobweb Plots)[17]。该图的横坐标为各个不同的参数，纵坐标为某个参数取值的百分位取值点，用直线连接同一组数据中落在纵坐标上的取值点，形成蛛网线，直线的分布规律即能表达参数之间的条相关性；并统计一组数据中相邻参数百分位取值之和，得到其统计分布图。蛛网线呈现“三角形分布”以及相邻参数百分位取值之和分布呈现“三角形分布”的程度越大，表示参数之间相互独立的程度越大。

选取PCBN模型得出的5 000组数据绘制百分位蛛网图，如图 7所示。发现V1-V10，V10-V11之间呈现明显的非“三角形分布”，表明这2组参数之间具有较强的相关性； V2-V3、V3-V4、V4-V5、V6-V7和V7-V8之间呈现明显的“三角形分布”，表明这5组参数之间相对独立；而V11-V2、V5-V6和V8-V9则呈现不明显的“三角形分布”，表明这3组参数存在弱相关性，该结论亦与图 4的结论较为吻合。

图7 参数联合分布的百分位蛛网图Fig.7 Percentile spider map of joint distribution

3.4 某地铁空推段安全可靠度评估

在构建的PCBN模型的基础上，利用蒙特卡罗法可以得到各节点指标的模拟值，为保证失效概率计算的精度，采用MCMC法，进行了5次107次M-H抽样，能够保证失效概率的精度达到0.01×10-5。在得到节点指标的模拟值后分别采用3种失效模式计算结构的失效概率，计算结果如图 8所示。

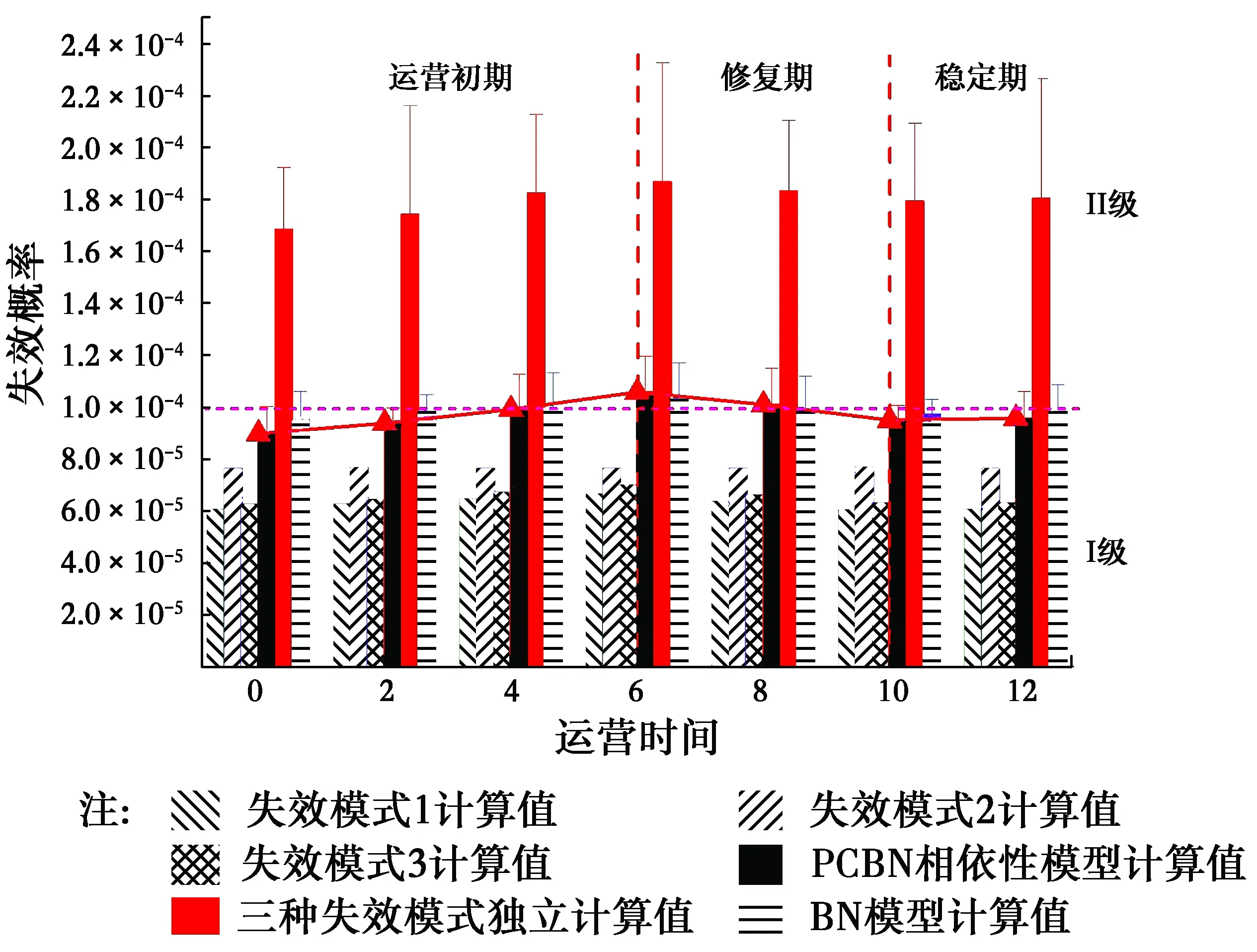
图8 失效概率计算结果Fig.8 Failure probability calculation

同时，在图 8中也对比3种不同的失效模式以及节点之间独立下的失效概率计算值，发现若只考虑一种失效模式得出的结构失效概率比通过PCBN模型得到失效概率的少20%～30%左右，地铁结构偏于安全。且随着实际工程情况的变化，各个失效模型计算得到的失效概率值变化幅度很小，以失效模式2的计算值为例，从0到12月，其失效概率最大变化量在1%左右，表明用单一的失效模型并不能很好地描述盾构结构的安全状态。若考虑3种失效模式的独立叠加，则发现其失效概率是PCBN模型的2倍左右，偏向危险，且对比PCBN模型和独立模型计算值的误差线发现，独立模型的误差线较长。比如，进行5次抽样后得到运营2个月的评估结果，PCBN模型和独立模型的标准差分别为0.059 3×10-4和0.442 1×10-4，相差7.46倍，表明独立模型计算结构的稳定性很差，也不适合作为盾构地铁结构的安全评判方法。另外，对比PCBN模型和传统BN模型计算值发现，随着运营时间变化，PCBN模型能够更好的描述节点参数之间的相依结构，其计算值较BN模型变化幅值更大，表明PCBN模型计算值能够更敏感的捕捉到结构状态信息的变化。综合以上因素，选用PCBN模型计算值作为盾构结构安全状态的最终评判值。

武汉地铁3号线越汉江空推段运营6个月后，其区间渗透水病害非常明显，并在盾构地铁的局部发现微小裂缝。依据可靠性值将运营地铁结构的安全状态分为4个等级，其中I级和II级分界线的失效概率值为1.0×10-4。从图 8中可知，通过PCBN模型发现，空推区监测段地铁结构的失效概率在运营6个月后，由0.898×10-4增加到1.061×10-4，其安全等级由I级变化到了II级，该评估结果的变化趋势与实际工程中出现的预警信息较为一致。相关地铁运营安全管理部门组织相关专家讨论后，决定对相应区段的病害部位采用修复措施，经过处理后，地铁内的渗透水病害明显减少。由图 8可知，在经过修复后，地铁结构的失效概率从6月到10月由1.061×10-4减少到0.954×10-4，且安全等级回到了I级，表明修复措施明显改善了地铁安全状态。而后的10～12月，其失效概率从0.954×10-4变化到0.957×10-4，没有明显的波动，显示地铁结构的安全状态进入了平稳期，安全风险得到了控制。

通过对比PCBN模型得出的地铁安全状态与地铁工程中的实际风险信息非常吻合，其中，0～6月为运营初期，其结构失效概率有一定的增加趋势。而后6～10月为地铁结构的修复期，其失效概率明显减少，而10～12月为结构修复后的稳定期，其失效概率值基本保持不变，体现了PCBN模型对实际地铁运营安全管理有较好的指导效用。