深厚覆盖层中弱透水层厚度及连续性对渗流场的影响
2019-05-09王正成毛海涛王晓菊申纪伟唐鑫刘阳
王正成,毛海涛,2,王晓菊,3,申纪伟,唐鑫,刘阳
(1.重庆三峡学院 土木工程学院,重庆 404100;2.武汉大学 水利水电学院, 武汉 430072; 3.河海大学 环境学院,南京 210098;4.新疆农业大学 水利与土木工程学院,乌鲁木齐 830052)
在中国西北地区建坝,常遇到深厚覆盖层[1],如察汗乌苏水电站、下坂地水利枢纽工程、500水库。此类坝基不仅仅局限于中国,Tarbela Dam(巴基斯坦)、Aswan High Dam(埃及)、Morelos Dam(墨西哥)和Wolf Creek Dam(美国)的坝基也同样是深厚覆盖层[2-3]。调查研究表明,中国西北深厚覆盖层中常存在弱透水层,该土层透水性差,隔水作用显著[4],但往往存在厚度较薄和不连续等缺陷。
学者们针对深厚覆盖层中连续且等厚的弱透水层开展了相关研究。吴梦喜等[5-6]研究表明,含弱透水层的深厚覆盖层坝基采用垂直防渗墙控渗时,弱透水层对渗流场有较大的影响。汪斌等[7]提出弱透水层的饱和渗透系数、土水特征函数和坡体结构系数共同决定水位升降过程中土体孔隙水压力、浸润线的分布。王正成等[8]研究表明,埋藏较深的弱透水层与防渗墙形成的半封闭式防渗体系,相比位置较浅的更能有效降低渗流量和抑制出逸坡降。采用ADINA针对上江坝工程进行分析,研究表明,当坝基采用半封闭式防渗墙时,渗流量、渗透坡降和应力-应变均小于允许值,该弱透水层能作为控渗依托层[9]。目前,关于弱透水层的厚度及连续性方面的研究鲜见,仍需开展大量研究工作进行深入研究。
本文借助有限元软件Seep/w建立数值模型,计算得出单宽渗流量及出逸坡降,并结合实际工程对比分析,探讨深厚覆盖层坝基中弱透水层的厚度、开口形式(开口在上游、开口在下游、上下游都有缺口)及开口长度对渗流场的影响,以期为含有弱透水层的深厚覆盖层坝基控渗方案的选择提供理论支撑,防止坝基发生渗透破坏。
1 非饱和土体渗流理论
非饱和土体的体积含水率θw及渗透系数k均为基质吸力um的函数[10]。非饱和土体中,水的表面张力使得土体孔隙中的水、气截面产生弯液面,水和气承受不同的压力,孔隙气压力和孔隙水压力的差值称为基质吸力[11]。土-水特征曲线可表征非饱和土体积含水率与基质吸力的关系,非饱和土渗流方程可表征渗透系数与基质吸力的关系。
基质吸力可以用Laplace公式来计算。
(1)
式中:um为基质吸力,kPa;ua为孔隙气压力,kPa;uw为孔隙水压力,kPa;Ts为表面张力,75 kPa;r1和r2为弯液面的短轴和长轴的半径。
非饱和土壤水分特征曲线方程[12]为
(2)
式中:θw为体积含水率;θs为土体饱和体积含水率;θr为土体残余体积含水率;αw为与进气值倒数相关的参数;nw为超过进气值后土-水特征曲线斜率相关的模型参数;mw为与非饱和土残余状态相关的模型参数,与nw的关系式为
(3)
非饱和土渗流方程[13]为
(4)
式中:k为土体渗透系数;ks为饱和渗透系数。
Seep/w中的公式能较好地反应饱和渗透系数与土体孔隙率之间的关系,文中采用该计算模型。
(5)
式中:ks0为土体初始饱和渗透系数;n为土体孔隙率;n0为土体初始孔隙率。
2 数值模型的建立
2.1 模型概况
黏土均质坝坝高8.3 m,坝顶宽6 m,坝前水头为6 m。坝基厚70 m,为深厚覆盖层坝基,坝基中间位置处有一层黏土(弱透水层),埋藏深度为35 m;除黏土层外均为砂土,坝体和坝基中的黏土层为同一种材料。坝基采用垂直防渗墙进行防渗,厚度为0.8 m,嵌入坝体2 m。模型断面如图1所示。
为探讨弱透水层厚度对渗流场的影响,模拟中,厚度取1~10 m,每次增加1 m,共计10种。探讨弱透水层不连续形式渗流场的影响,分为以下3种情况:1)工况a。弱透水层上游开口长度为20 m,厚度d=1 m,如图1(a)所示。2)工况b。弱透水层下游开口长度为20 m,厚度d=1 m时,如图1(b)所示。3)工况c。上、下游弱透水层皆短缺10 m,厚度d=1 m,如图1(c)所示。弱透水层上游开口长度L=0~60 m,每次延长5 m,共计13种。防渗墙深度为10~70 m,根据防渗墙是否穿过弱透水层和底端所在土层的性质,防渗墙可分为悬挂式防渗墙、半封闭式防渗墙和全封闭式防渗墙[14]。

图1 模型断面图
2.2 计算参数
非饱和土渗流过程中,土体含水率θw和渗透系数k随基质吸力变化,θw、k与基质吸力um的关系曲线,如图2、图3所示。

图2 土体体积含水率随基质吸力的变化曲线Fig.2 Varying curves of soil volumetric water content with matric

图3 土体渗透系数随基质吸力的变化曲线Fig.3 Variation curves of permeability coefficient of soil with matric
将黏土、砂土和防渗墙的孔隙率、干密度、重度、凝聚力和渗透系数等基本物理参数列入表1。

表1 材料的基本物理指标Table 1 Physical property of materials
3 数值模拟结果及分析
分别计算得出各工况下渗流量和出逸坡降。以d=1 m、L=20 m和S=50 m为例,作等势线图,如图4所示。

图4 大坝等势线Fig.4 Equipotential line of
由图4可知,等势线5~1集中在防渗墙内部,等势线5、2、1.5和1集中在弱透水层内部,可见,防渗墙和弱透水层能在很大程度上消减水头势能。
根据各工况数值模拟结果,分析渗流量和出逸坡降的变化情况,探讨弱透水层厚度和连续性对坝基渗流的影响。
3.1 弱透水层厚度对坝基渗流的影响
分析弱透水层厚度d对坝基渗流的影响时,弱透水层连续分布,埋藏深度35 m,处于坝基中间位置。作单宽渗流量随弱透水层厚度的变化曲线,如图5所示。

图5 单宽渗流量随弱透水层厚度的变化曲线Fig.5 Change curves of seepage discharge per unit width with aquitard
由图5可知,各曲线的变化规律一致,单宽渗流量随弱透水层厚的增大而降低。当防渗墙深度S=10~70 m时,随着弱透水层厚度的增大,单宽渗流量分别减小12.63%、16.28%、24.31%、61.9%、58.97%、53.47%和0.14%。由此可见,坝基分别采用悬挂式防渗墙、半封闭式防渗墙和全封闭式防渗墙控渗,弱透水层厚度由1 m增大至10 m时,单宽渗流量q分别降低12.63%~24.31%、53.47%~61.9%、0.14%。采用半封闭式防渗墙时曲线斜率最大,采用悬挂式防渗墙次之,采用全封闭式最小。
由此可得,处于中间位置处的弱透水层厚度对采用半封闭式防渗墙控渗时的单宽渗流量影响最大,悬挂式防渗墙次之,全封闭式防渗墙最小。
出逸坡降J随弱透水厚度d的变化曲线如图6所示。
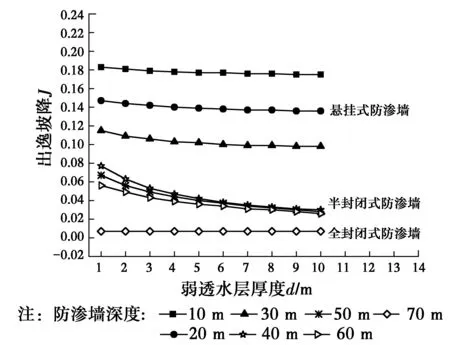
图6 出逸坡降随弱透水层厚度的变化曲线Fig.6 Change curves of exit gradient with aquitard
由图6可知,各曲线的变化规律同图5一致,都是随着弱透水层厚度d的增加而减小。当防渗墙深度S=10~70 m,弱透水层厚度d由1 m增大10 m时,渗透坡降J分别减小4.37%、7.48%、14.78%、61.04%、58.21%、53.57%和0%。坝基采用悬挂式防渗墙、半封闭式防渗墙和全封闭式防渗墙时,渗透坡降分别降低4.37%~14.7%、53.57%~61.04%、0%。
由此可得,处于中间位置处的弱透水层厚度对采用半封闭式防渗墙控渗时的出逸坡降影响最大,悬挂式防渗墙次之,全封闭式防渗墙最小。
3.2 弱透水层的不连续形式对坝基渗流的影响
分别计算得出工况a、b、c对应的单宽渗流量和出逸坡降。作单宽渗流量随防渗墙深度的变化曲线,如图7所示。

图7 单宽渗流量随防渗墙深度的变化曲线Fig.7 Change curves of seepage discharge per unit width with cutoff wall
当防渗墙深度为10~30 m(区域Ⅰ)时为悬挂式防渗墙,工况a、b、c对应的单宽渗流量仅相差0~2×10-4m3/s·m;当防渗墙深度为70 m(区域Ⅲ)时为全封闭式防渗墙,工况a、b、c对应的单宽渗流量相等,为7.26×10-4m3/s·m。
当防渗墙深度S=40~60 m(区域Ⅱ)时,工况a中,下游弱透水层和防渗墙形成半封闭式防渗体系,工况b中,上游弱透水层和防渗墙形成半封闭式防渗体系,工况c为悬挂式防渗体系。工况a、b对应的单宽渗流量q分别为8.03×10-3~1.13×10-2m3/s·m和8.07×10-3~1.15×10-2m3/s·m,工况c对应的单宽渗流为8.26×10-3~1.22×10-2m3/s·m。
可见,工况c对应的单宽渗流量高于工况a、b,工况a、c的差值为2.3×10-4~9×10-4m3/s·m,工况b、c的差值为1.9×10-4~7×10-4m3/s·m;工况b对应的单宽渗流量高于工况a,差值为2×10-4~1.1×10-3m3/s·m。
作出逸坡降随防渗墙深度的变化曲线,如图8所示。
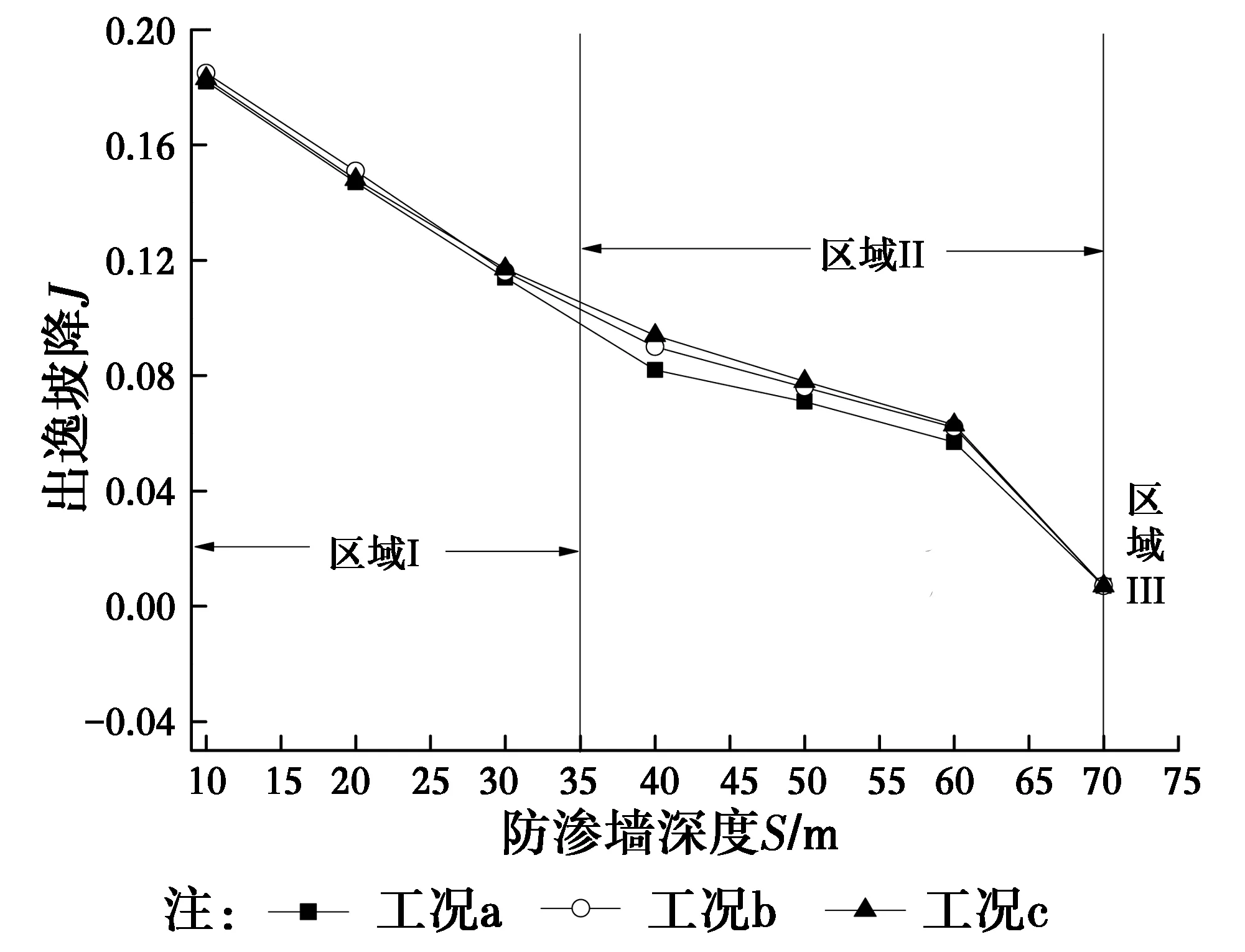
图8 出逸坡降随防渗墙深度的变化曲线Fig.8 Change curves of exit gradient per unit width with cutoff wall
图8的变化规律同图7一致,当S=10~30 m(区域Ⅰ)时为悬挂式防渗墙,工况a、b、c对应的出逸坡降仅相差0.001~0.004。当S=70 m(区域Ⅲ)时为全封闭式防渗墙,工况a、b、c对应的出逸坡降均为0.007。当S=40~60 m(区域Ⅱ)时,工况c对应的单宽渗流量高于工况a、b,工况a、c的差值分别为:0.006~0.012,工况b、c的差值分别为0.001~0.004。工况b对应的渗透坡降高于工况a,差值为0~0.008。
综上所述,工况a在控制单宽渗流量和抑制出逸坡降方面的效果最好,工况b次之,工况c最差。
3.3 弱透水层上游开口长度对坝基渗流的影响
由于工况a(上游开口长度为20 m)在控制单宽渗流量和抑制出逸坡降方面的效果优于工况b、c,因此,针对弱透水层上游的开口长度作进一步分析。分析弱透水层上游开口长度对坝基渗流的影响时,d=1 m,埋藏深度为35 m。
作单宽渗流量随弱透水层上游开口长度的变化曲线如9所示。

图9 单宽渗流量随弱透水层开口长度的变化曲线Fig.9 Change curves of seepage discharge per unit width with open length of
由图9可得,各曲线变化规律一致,单宽渗流量随L增加而增大。以防渗墙深度S=60 m为例,L=0~60 m对应的单宽渗流量q为7.78×10-3~8.39×10-3m3/s·m,降低了7.84%。
当S=10~50 m和70 m时,L由0增大至60 m时,q分别增大2.53%、3.49%、4.9%、1.33%、1.06%、0%,曲线的斜率i=0~2.33×10-5。综上所述,弱透水层上游开口长度的大小对单宽渗流量q影响较小。
作出逸坡降J随弱透水层上游的开口长度的变化曲线,如图10所示。

图10 出逸坡降随弱透水层开口长度的变化曲线Fig.10 Change curves of exit gradient with
图10和图9中各曲线的变化规律一致,J随L的增加而增大。当S=10~70 m,L增大至60 m时,出逸坡降分别增大2.76%、2.74%、5.31%、11.69%、10.45%、7.14%、0%,曲线的斜率i=0~1.5×10-4。L增加至60 m时,出逸坡降J增大0~0.009。可见,弱透水层的上游开口长度对出逸坡降的影响不显著。
弱透水层开口长度增大,单宽渗流量和出逸坡降仅增大。0~1.4×10-3m3/s·m、0~0.009,可见,弱透水层的开口长度对单宽渗流量和出逸坡降影响较小。
4 算例分析
4.1 弱透水层厚度对坝基渗流的影响
某大坝(工程a)坝顶高程为2 108 m,坝顶宽10 m,建基面高程为1 859 m,水库正常蓄水位为2 100 m。心墙顶端高程为2 107.6 m,墙顶宽3 m,心墙料为黏土,防渗墙深度为56 m,厚度为1 m。坝基从上至下分为五层:Ⅰ岩组为漂卵石,厚49.7~58.3 m;Ⅱ岩组为低液限黏土,厚9.4~24 m;Ⅲ岩组为砾卵石,厚59.6~71.5 m;Ⅳ岩组为碎块石,厚14.0~38.4 m;Ⅴ岩组为砂砾石,厚0~52.1 m;深厚覆盖层坝基坐落于寒武岩。岩层分布如图11所示。

图11 坝基岩层分布Fig.11 The rock distibution of dam
Ⅱ岩组为低液限黏土层,以黏粒和粉粒为主,可视为弱透水层。坝体、深厚覆盖层坝基、黏土心墙和防渗墙的渗透系数如表2所示。
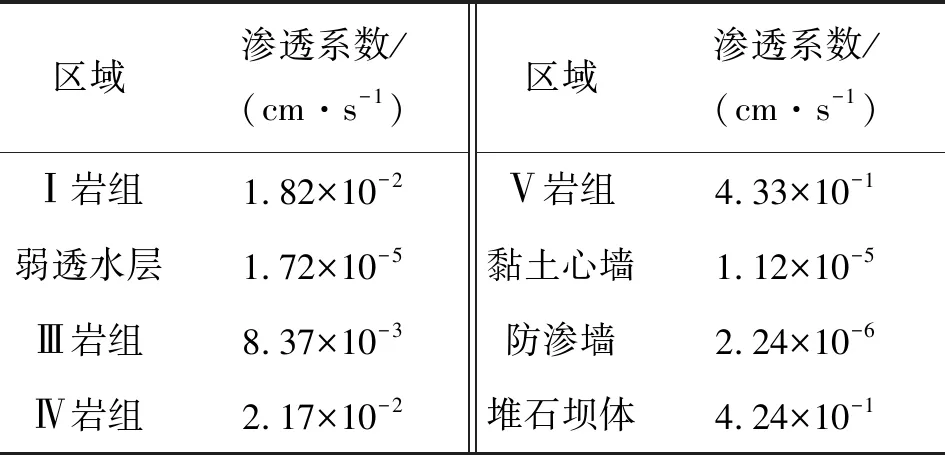
表2 坝体及坝基渗透系数Table 2 The calculation parameters of dam and dam foundation
分析弱透水层厚度对渗流的影响,拟定2种工况。1)工况1(ZK1)。Ⅰ~Ⅴ岩组的厚度分别为:56、24、70.5、14和33.15 m,防渗墙深度为57 m,如图12(a)所示。2)工况2(ZK4)。Ⅰ~Ⅳ岩组的厚度分别为:50.29、11.43、60.15和36.58 m,该断面没有Ⅴ岩组,防渗墙深度为57 m,如图12(b)所示。
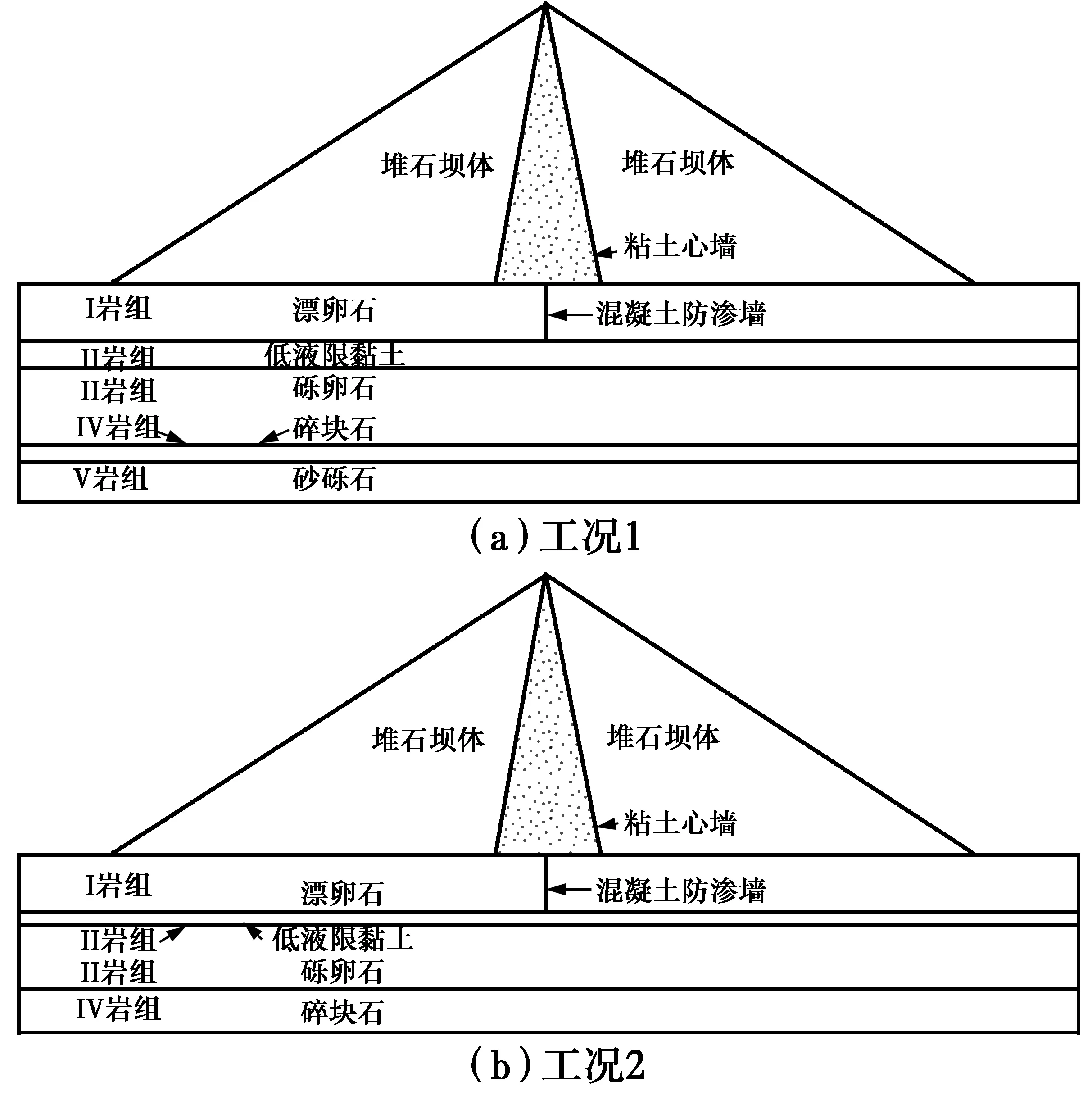
图12 大坝断面图
计算得出工况1、2对应的单宽渗流量和出逸坡降,列入表3。
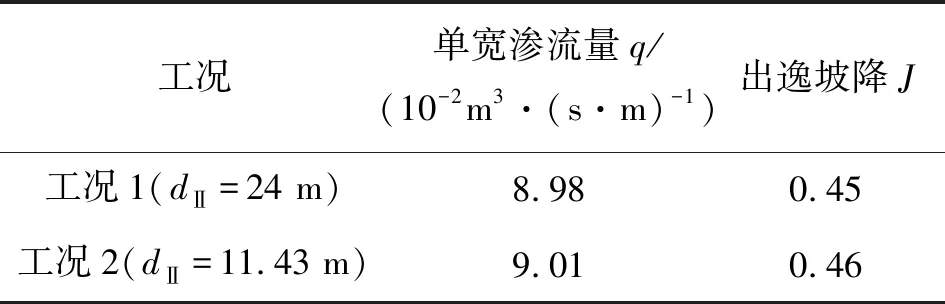
表3 单宽渗流量和出逸坡降Table 3 Seepage discharge per unit width and exit gradient
由表3可得,当防渗墙深度一定时,弱透水层厚度由11.43 m增大至24 m时,q由9.01×10-2m3/s·m降低至8.98×10-2m3/s·m,降低了3×10-4m3/s·m,为初始量的0.33%;J由0.46减小至0.45,减小了0.01,为初始量的2.22%。可得弱透水层厚度d越大,单宽渗流量q和出逸坡降J越小。
结合3.1节综合分析,数值模拟中弱透水层厚度增大,q和J分别减小0.14%~61.9%、0%~61.04%。数值模拟和工程实例分析可得出一致结论,单宽渗流量和出逸坡降随弱透水层厚度的增加而减小。
4.2 弱透水层连续性对坝基渗流的影响
某大坝(工程b)最大坝高78 m,坝顶宽10 m,筑坝材料为砂砾石,坝顶高程为2 966.00 m,设计水位为2 745.00 m。坝基覆盖层厚150 m,坝体和坝基均采用厚1 m的混凝土防渗墙控渗。坝基中黏土层厚度为3.97 m,埋藏深度为73 m(处于坝基中间位置),长度为243.5 m。大坝剖面如图13(a)所示。
坝体料、深厚覆盖层坝基、混凝土防渗墙、石渣的计算参数如表4所示。

表4 坝体及坝基渗透系数Table 4 Permeability coefficient of dam and dam foundation
由表4可得,黏土可视为弱透水层。为探讨坝基中弱透水层的连续性对渗流的影响,增设工况2作对比分析。1)工况1。弱透水层上游开口长度为30.5m,如图13(a)所示。2)工况2。弱透水层从上游贯穿至防渗墙,如图13(b)所示。

图13 大坝断面图
计算得出工况1、2对应的单宽渗流量q和出逸坡降J,将结果列入表5。

表5 单宽渗流量和出逸坡降Table 5 Seepage discharge per unit width and exit gradient
当坝基中弱透水层的开口长度由0 m增大至30.5 m时,q、J分别增大5.07%和5.41%。可见,单宽渗流和出逸坡降随弱透水层开口长度的增加而增大。
结合3.3节综合分析,数值模拟中当开口长度由0 m增大至60 m时,单宽渗流量和出逸坡降分别增大0%~7.84%和0%~10.45%。由此可得,单宽渗流量和出逸坡降随弱透水层开口长度增加而增大,但影响较小。
4.3 数值模拟的精确性验证
为了验证数值模拟的可靠性,将模拟值与实测值进行对比分析,文中工程a和b的工况1与工程实际一致,实际中也均有详实的渗流观测资料。将实测值和模拟值对比如下表6所示。

表6 渗流量和出逸坡降实测值和模拟值Table 6 Measured and simulation value of seepage discharge and exit gradient
由表6可得,工程a和工程b渗流量的误差分别为 4.67%和5.84%,出逸坡降的误差分别为2.17%和4.88%。二者误差均在5%左右,该计算精度在水利工程中是符合规范要求的。误差可能是文中将部分覆盖层进行简化所致。
5 讨论
5.1 弱透水层埋藏深度分析
当弱透水层埋藏较浅时,其防渗作用相当于水平铺盖,以二元结构为突出代表,该类结构坝基的研究已经较为成熟[15]。当弱透水层埋藏较深时,建议做成全封闭式。当弱透水层处于坝基中间位置时,渗流规律尚不明朗,需要深入研究。因此,在分析弱透水层厚度对坝基渗流的影响时,弱透水层埋藏深度为35 m,处于中间位置,具有代表性。
5.2 弱透水层的连续性对渗控的影响
对比分析弱透水层的不连续形式,工况a在控制单宽渗流量和抑制出逸坡降方面的效果最好,工况b次之,工况c最差。因此,若坝基中存在不连续的弱透水层,在设置垂直防渗墙时,应尽可能使下游弱透水层和垂直防渗墙形成半封闭防渗体系,利于坝基控渗,杜绝防渗墙上下游弱透水层均存在缺口的不利情况。
5.3 防渗墙形式对渗控的影响
弱透水层上游的开口长度对单宽渗流量和出逸坡降影响较小,可以借助坝基控渗形式进行解释,当S=10~30 m时,坝基采用悬挂式防渗墙控渗,已有研究表明悬挂式防渗墙在控制渗流量和抑制出逸坡降方面的效果不显著[16];当S=40~60 m时,下游弱透水层与防渗墙已经形成半封闭式联合防渗体系,上游弱透水层是否连续对坝基渗流影响较小;当S=70 m时,为全封闭式,防渗墙几乎承担了全部隔水任务,弱透水层的隔水效果微弱;综合分析可得,渗流场受弱透水层上游开口长度影响较小。
6 结论
基于非饱和土体渗流理论,建立数值模型针对弱透水层的厚度及连续性进行研究,并结合实际工程进行分析,得出以下结论:
1)单宽渗流量和出逸坡降随中间位置处弱透水层厚度增加而降低,分别降低0.14%~61.9%、0%~61.04%。此外,弱透水层厚度对采用半封闭式防渗墙控渗时的渗流场影响最大,悬挂式防渗墙次之,全封闭式防渗墙最小。
2)针对中间位置处弱透水层的不连续形式进行分析可得,开口在上游的弱透水层与防渗墙形成的半封闭式联合防渗体系的控渗效果最优,开口在下游的弱透水层次之,防渗墙上下游都存在开口时效果最差。工程中设置防渗墙时,建议下游弱透水层和防渗墙形成半封闭式联合防渗体系,避免防渗墙上下游弱透水层皆存在缺口的不利情况。
3)单宽渗流量和出逸坡降随中间位置处弱透水层上游开口长度增加而增大,分别增大0%~7.84%和0%~10.45%;曲线斜率小,增大幅度小,可见,弱透水层的开口长度对渗流场影响较小,其原因在于,3种防渗墙形式下上游弱透水层隔水作用微弱。
