单翼大挠性航天器全局模态动力学建模及试验

袁秋帆，王超磊，齐乃明，曹世磊

(1. 上海系统工程研究所，上海 201109；2. 北京仿真中心航天系统仿真重点实验室，北京 100854； 3. 哈尔滨工业大学航天工程系，哈尔滨 150001)

0 引 言

随着航天科技的发展，挠性结构尺寸和重量逐渐增加，挠性附件的振动会带动中心刚体运动，这种耦合形式可称为小中心刚体-大挠性附件的耦合形式。在小角度和小位移机动时，这种航天器的挠性结构会产生振动，但一般不会出现较大变形，可以将其简化为线性系统处理。对其进行控制器设计的基础是建立合适的动力学模型。传统的约束模态动力学模型采用悬臂状态下的挠性振动模态方程与中心刚体运动方程构成刚柔耦合动力学方程。全局模态法又被称为非约束模态法，在20世纪70年代到80年代，文献[1-4]详细研究了非约束模态法，即使用整个航天器自由-自由状态下的模态振型进行模态展开，振型描述函数包含挠性结构和中心刚体，推导了非约束模态的正交性及其惯性完备性准则。Hablani[2,4]指出非约束模态建模和约束模态建模的精度与刚柔惯量比有关，指出刚柔惯量比较小时，约束模态法建立的动力学模型将有比较大的误差。Goal[5]指出约束模态法动力学模型采用约束模态描述了刚体与挠性结构之间的耦合作用，而全局模态法动力学模型描述了挠性航天器整体的动力学特性，是输入与输出的耦合特性。

以上研究中仅考虑了挠性航天器的姿态运动，然而当中心刚体占比较小时，大挠性结构的振动将同时影响小中心刚体姿态运动和位置运动，在建模时不能仅考虑本体姿态运动与挠性振动的耦合特性，还要考虑本体位置运动与挠性结构振动的耦合特性。章仁为[6]采用约束模态法建立了动力学模型，同时考虑了姿态耦合特性和位置耦合特性，并采用转动耦合系数和平移耦合系数分别描述。Pgasbarri[7]采用带有双侧对称帆板的气浮式模拟器研究了挠性航天器动力学，指出双侧对称帆板构型的航天器存在对称模态和反对称模态，对称模态对应位置耦合特性，反对称模态对应姿态耦合特性。徐小胜等[8]基于刚柔耦合动力学模型，采用了约束模态频率估计了非约束模态频率。吕旺等[9]对采用类似的方法对非约束模态频率进行了估计，并与在轨试验结果进行了对比，在挠性结构比较小的情况下，估计误差在15%以内，其方法仍是基于刚柔耦合动力学模型。

2014年，Gasbarri[10]采用有限元法分析了含有多个大挠性结构的航天器的非约束模态动力学特性，建立了包含位置耦合特性和姿态耦合特性的完整的非约束模态动力学模型，并且定义了中心刚体“模态振型”(the ‘shape’ of the satellite)的概念，将中心刚体的刚体运动和挠性结构振动一并纳入模态振型。文献[11-12]采用瑞利瑞兹法计算了带有双侧对称帆板的航天器的全局模态振型，并给出了模态频率随着帆板长度、中心刚体惯量和帆板构型的改变的变化规律，采用对称模态振型和反对称模态振型分别描述了位置耦合特性和姿态耦合特性。

以上研究均采用了双侧对称帆板的航天器构型，姿态耦合特性和位置耦合特性不会存在于同一阶全局模态中。而当航天器仅带有单侧挠性结构时，在其同一阶全局模态中，同时存在姿态耦合特性和位置耦合特性，目前相关的研究较少。

大部分航天器采用了双侧对称帆板构型，有一小部分航天器采用了单侧帆板构型，比较典型的有中国风云三号、四号卫星，美国NASA的Aura卫星、欧洲太阳神卫星、日本的大地卫星等，研究单侧挠性航天器的建模问题有重要的工程意义。

本文将针对小中心刚体-单侧大挠性结构构型的航天器，通过定义广义全局模态振型提出了一种全局模态动力学模型，采用统一形式描述整体刚体运动和整体挠性变形，与现有研究相比，形式更加简洁统一，解决了单侧大挠性航天器的动力学建模问题。结合瑞利瑞兹法分析非约束模态频率随着质量比和惯量比的变化而变化的情况，与有限元模型比对了动力学响应，并且构建试验系统，进行了非约束模态频率的测量和对比分析。

1 全局模态法动力学建模

1.1 全局模态振型

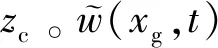
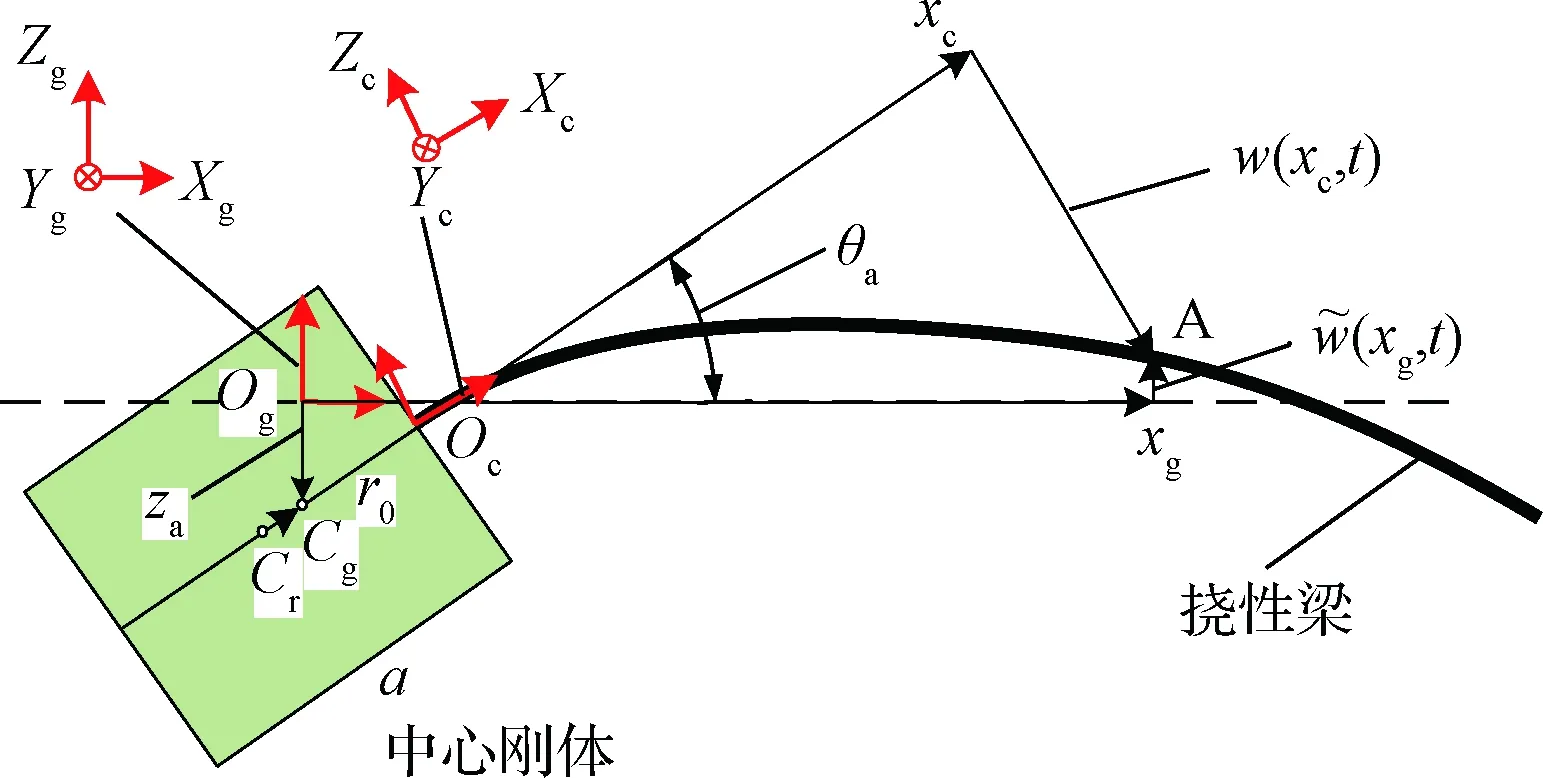
图1 全局模态法坐标系定义Fig.1 The definition of constrained modal shape function

假设za为小位移，θa为小角度，则有如下近似的挠度关系

(1)

式中：r0=CgOc，l为挠性梁长度，xg∈[-a+r0,r0+l]，xc∈[0,l]，浮动坐标系下的挠度可以模态展开为

(2)

式中：φk(xc)为非约束状态下，在浮动坐标系下描述的挠性结构模态振型。

在非约束边界条件下，第k阶挠性模态振动时，中心刚体也有相应的位移和角度变化。定义整体质心的模态位移为zak，绕质心的模态转角为θak，则整体质心的位移可以表示为模态位移的叠加，整体刚体转动角度可以表示为模态转角的叠加，即

则式(1)可以转化为

(3)

式中：

(4)

为全局模态振型。

定义整体的转动运动为第一阶刚体模态，整体的平移运动为第二阶刚体模态，则这两阶模态振型函数可由式(4)表示，第一阶刚体模态振型可以表示为

(5)

第二阶刚体模态振型可以表示为

(6)

挠性振动模态振型为第三阶以及更高阶模态振型，模态振型函数表示为

(7)

式中：k=3,4,5…。

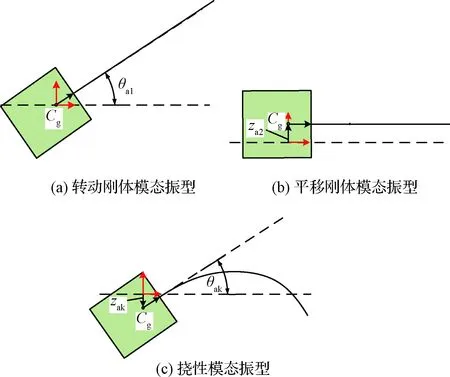
图2 全局模态振型Fig.2 Global modal shape

至此，刚体的运动和挠性结构的振动均通过式(4)描述的全局模态振型表示。定义ρrAr,ρbAb和ρA分别为中心刚体、挠性梁和整体沿OgXg轴的线密度分布。定义

式中:Er和Ir分别为中心刚体沿xg方向的杨氏模量和截面惯性矩，Eb和Ib分别为挠性梁沿xg方向的杨氏模量和截面惯性矩。定义Jgr,Jgb和Jg分别为中心刚体、挠性梁和整体绕OgYg轴的转动惯量。定义Mg=Ma=Mr+Mb为总质量，Mr为刚体质量，Mb为挠性结构质量。

定理1. 由式(4)定义的非约束模态振型满足正交性，并且

(8)

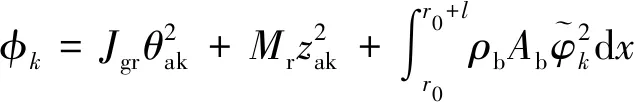
为狄拉克函数。

证.文献[11]指出当单个挠性梁满足两端约束条件为自由、简支和固定三种简单约束时，模态振型是正交的，该结论可以通过边界条件方程简单推导得出，给出了判断模态振型正交性的一个简便的方法。中心刚体-挠性梁系统整体满足自由-自由的边界条件，按照文献[11]的理论，全局模态振型的正交性是显然的。

1.2 动力学方程

整体动能为

(9)

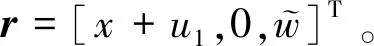
整体势能为

(10)

又平面内应变与挠度的关系为

(11)

设沿着Zg轴方向施加的外力为F，施加位置为xf g，绕与Yg轴平行的轴施加的外力矩为T，施加位置为xτg，则外力做功的变分可以表示为

(12)

根据哈密顿原理有

(13)

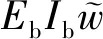
(14)

其中，δ(x)为狄拉克函数。

(15)

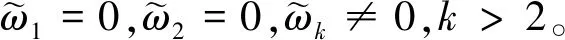
1)当k=1时，计算得φ1=Jg，式(15)转化为

(16)

式(16)与刚体姿态动力学方程一致，此时第一阶全局模态坐标η1为整体作为刚体时的转动角度。

2)当k=2时，计算得φ2=Mg，式(15)转化为

(17)

式(17)与刚体位置动力学方程一致，第二阶全局模态坐标η2为整体作为刚体时的平移位置。

将式(15)添加阻尼比，考虑前Nm阶模态，将全局模态动力学方程写成矩阵形式为

(18)

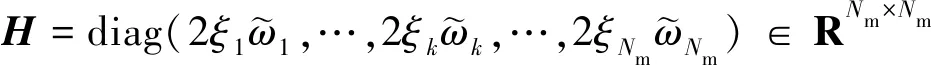
与约束模态的刚柔耦合动力学模型相比，全局模态动力学模型采用了统一的形式描述整体的刚体运动和挠性振动，形式上更加简洁，由于没有采用悬臂模态振型的正交性假设，对小中心刚体-大挠性结构的挠性航天器构型，全局模态动力学模型要更加精确。

1.3 非约束模态频率计算

对于中心刚体-挠性梁这类简单结构，可以利用全局模态振型构造瑞利瑞兹法的特征参数，采用瑞利瑞兹法计算全局模态振型对应的非约束模态频率。

首先建立第一阶模态基振型的多项式函数，设

X1(x)=a0+a1x+a2x2+a3x3+a4x4

(19)

为描述简便，首先认为挠性梁长度为1，约束条件表达为

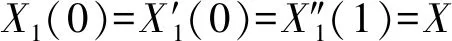
(20)

代入式(19)解出

X1(x)=a4(6x2-4x3+x4)

(21)

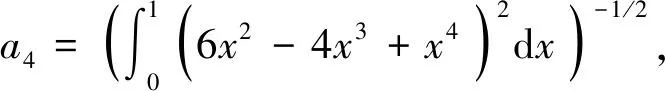
(22)

每一阶正交基均进行归一化处理，

(23)

当挠性梁长度为l时，其正交基可以表示为

(24)

第k阶全局模态振型由中心刚体的模态角度θak，模态位移zak和浮动坐标系下的模态振型φk组成，瑞利瑞兹法的基本原理是，针对一阶模态，其模态动能的最大值等于模态势能的最大值，即(EK)k_max=(EP)k_max。

考虑第k阶全局模态，

令ηk(t)=sin(ωkt)，根据式(9)和式(10)定义的动能和势能方程，可得

(25)

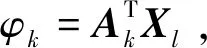
A=[A1,…,ANx]T，Xl=[Xl1,…,XlNx]

Nx为基振型个数。令

M和K分别为广义质量和刚度矩阵。求取(KE)k_max和(PE)k_max的雅克比矩阵

(26)

(27)

根据挠性结构特征方程

(K-λ2M)u=0

(28)

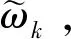
2 仿真分析

本章采用一个固定尺寸的挠性梁和一个边长为变量的中心刚体构成中心刚体-挠性梁系统，分析全局模态法对非约束模态频率和模态振型的计算精度，并且分析模型的动态响应精度。基本模型如图3所示，中心刚体为边长为的立方体，其他参数如表1所示。

图3 仿真基本结构Fig.3 The basic structure for simulation

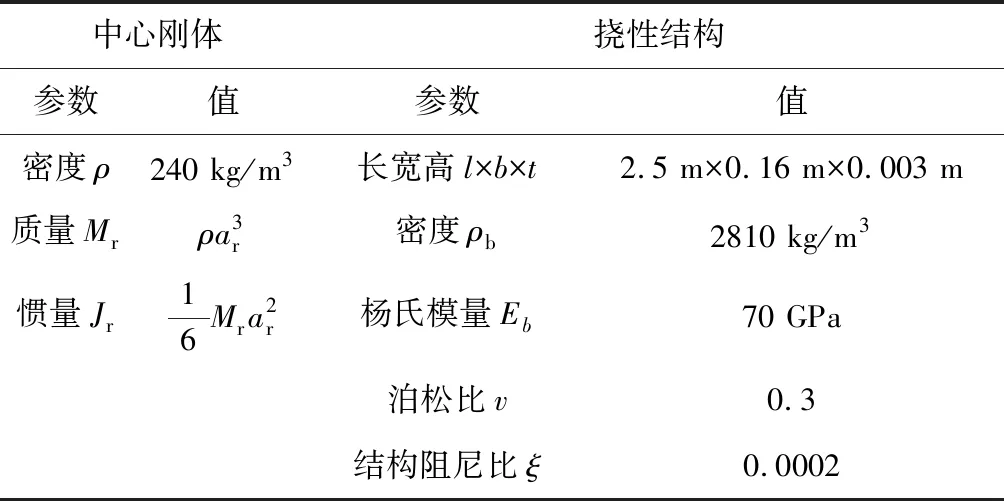
中心刚体挠性结构参数值参数值密度ρ240 kg/m3长宽高l×b×t2.5 m×0.16 m×0.003 m质量Mrρa3r密度ρb2810 kg/m3惯量Jr16Mra2r杨氏模量Eb70 GPa泊松比v0.3结构阻尼比ξ0.0002

2.1 非约束模态频率

2)在λJ<1的区间内，随着中心刚体的减小，非约束模态频率逐渐增大，当进入λm<1的区间内，非约束模态频率随着中心刚体的减小而增大的速率更快。可知，非约束模态频率与刚柔惯量比、质量比是一一对应的。

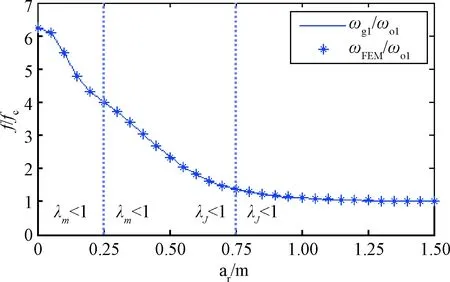
图4 非约束模态频率Fig.4 Unconstrained modal frequencies

2.2 非约束模态振型

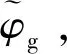
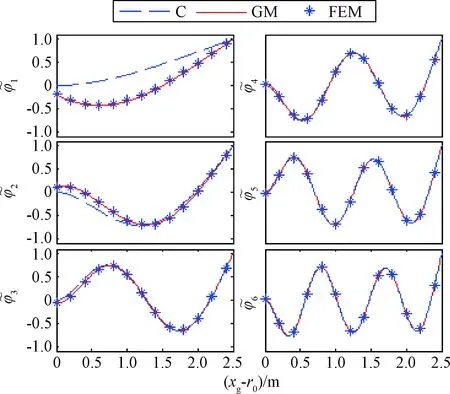
图5 非约束模态振型Fig.5 Unconstrained modal shapes

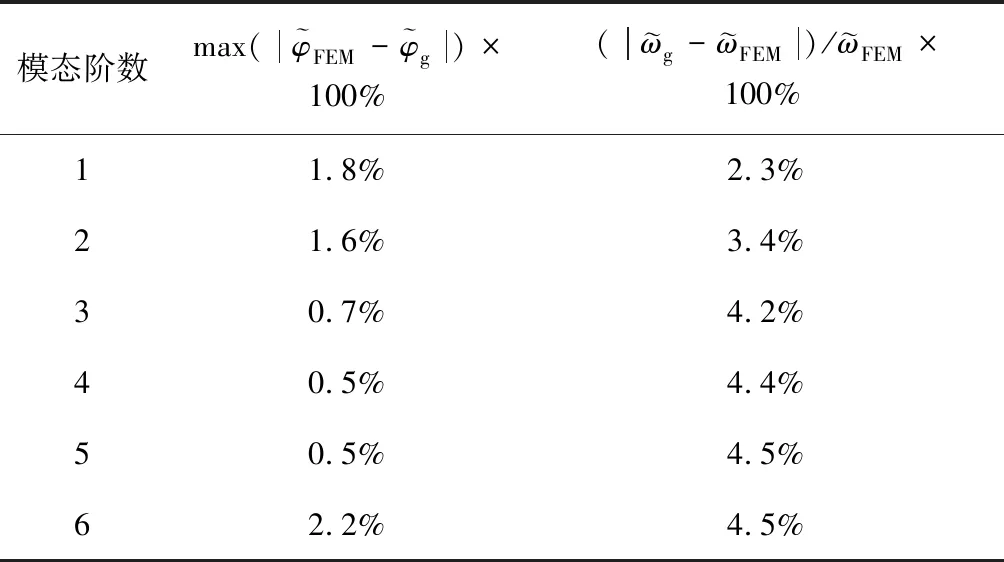
模态阶数max(φFEM-φg)×100%(ωg-ωFEM)/ωFEM×100%11.8%2.3%21.6%3.4%30.7%4.2%40.5%4.4%50.5%4.5%62.2%4.5%

2.3 动态响应

为了进一步验证全局模态动力学模型的准确度，在中心刚体上施加的力F和力矩T，如图6所示，采用所建立的全局模态动力学模型和有限元法计算模型的动力学响应，对比中心刚体转角θ、位置z和挠性结构的端部位移ztip，结果如图7、图8和图9所示。图中，“GM”表示全局模态法计算结果，“FEM”表示有限元法计算结果。

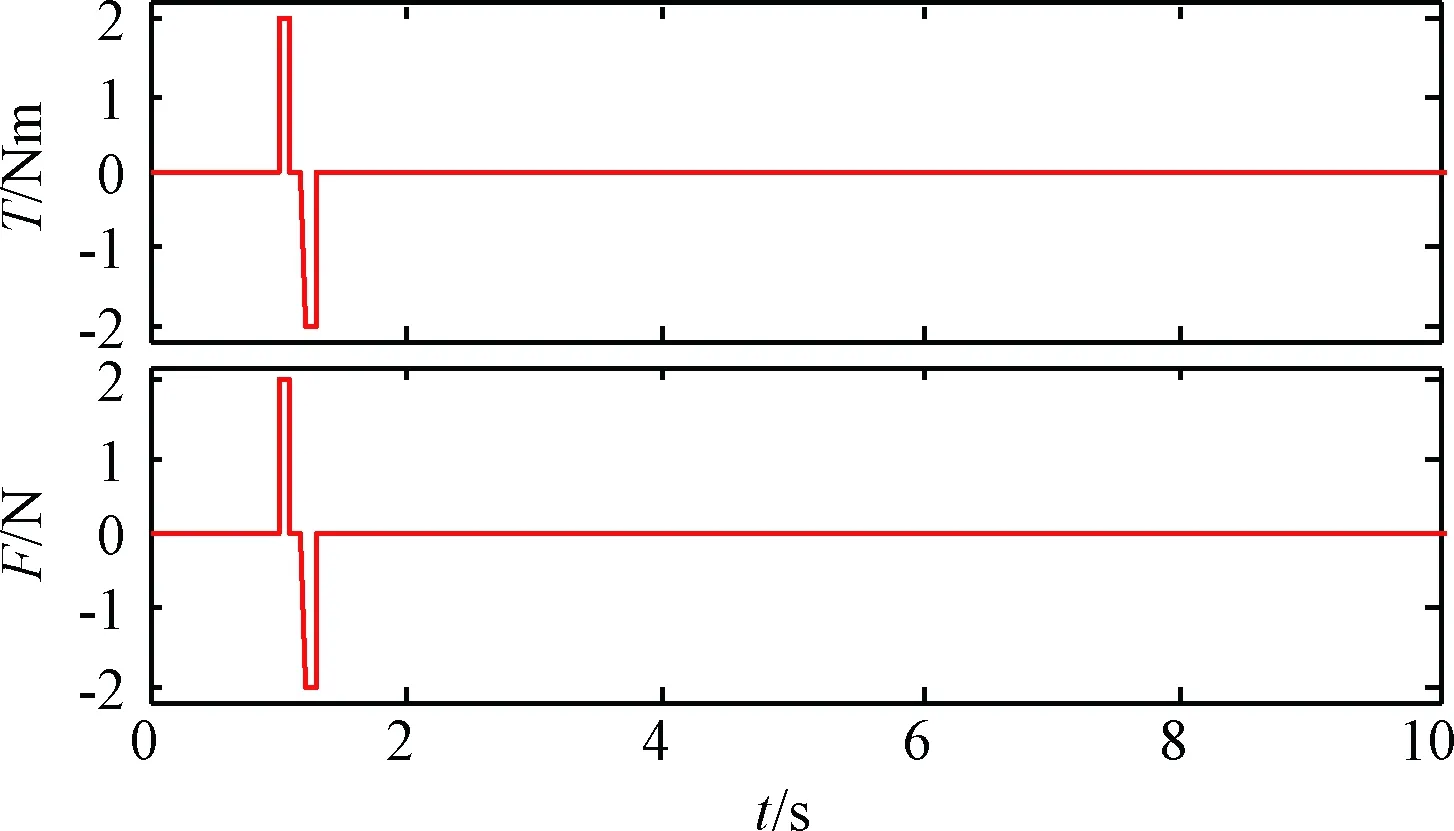
图6 施加的力和力矩Fig.6 Applied force and torque

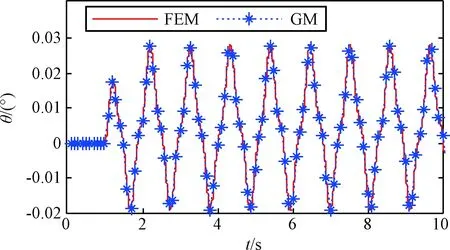
图7 中心刚体角度响应Fig.7 The responding angle of the rigid body

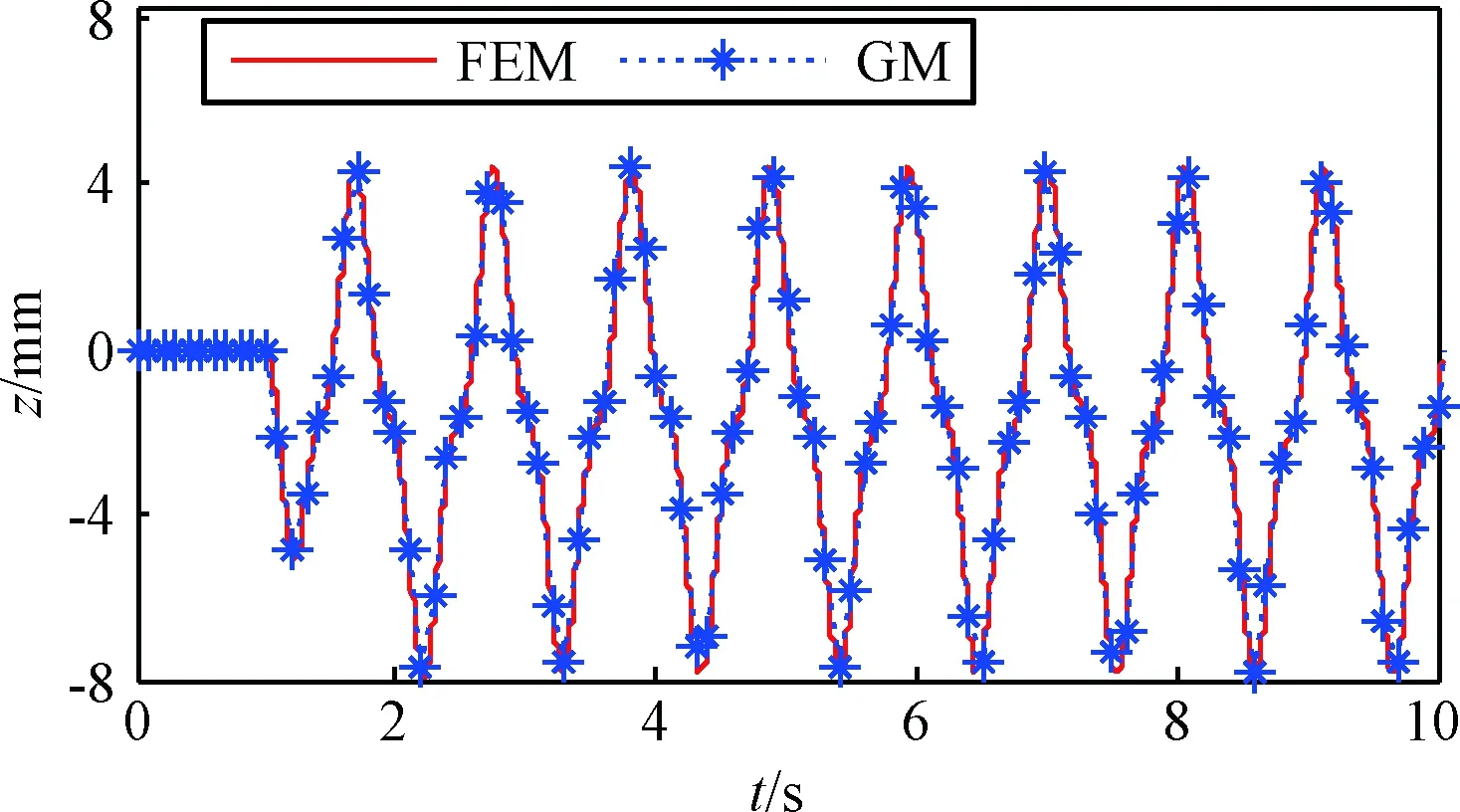
图8 中心刚体位置响应Fig.8 The responding displacement of the rigid body

根据结果分别计算最大误差，如表3所示，可见有限元计算结果和动力学模型还是比较相近的。

表3 动态响应误差Table 3 Dynamic response errors

3 试验分析

为了进一步验证全局模态动力学模型的准确性，搭建了如图所示的试验系统，中心刚体为三自由度气浮模拟器，下方安装有气足，可以实现无摩擦的两个水平轴向的平移运动和绕垂直轴的旋转运动。挠性板连接在中心刚体上，端部安装有支撑气足和端部质量块，端部质量块用于降低挠性结构的基频，提高挠性结构的质量和惯量占比。挠性结构的尺寸同表1，中心刚体的尺寸为0.9 m×0.9 m×1.2 m，中心刚体重量为240 kg。当中心刚体的气足关闭，挠性板支撑气足打开时，挠性板处于悬臂状态；当中心刚体的气足和挠性板支撑气足同时打开时，整体处于非约束状态。在挠性板根部安装有力矩传感器，用于测量振动。

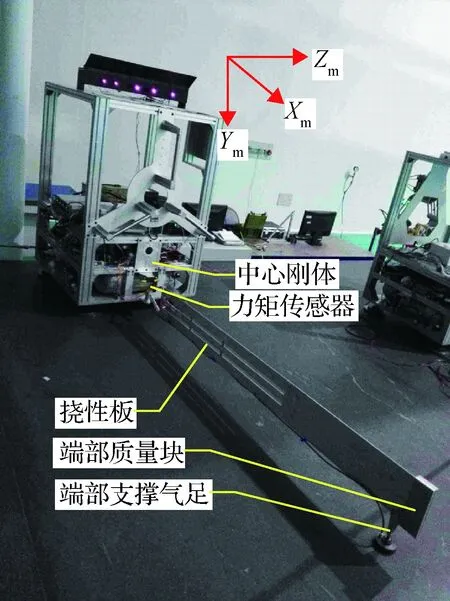
图10 施加的力和力矩Fig.10 Applied force and torque

3.1 悬臂模态频率测试

将中心刚体的气足供气关闭，只开启挠性板端部支撑气足的供气，此时挠性板处于悬臂状态，在悬臂状态下对其进行敲击，测量自然振动。

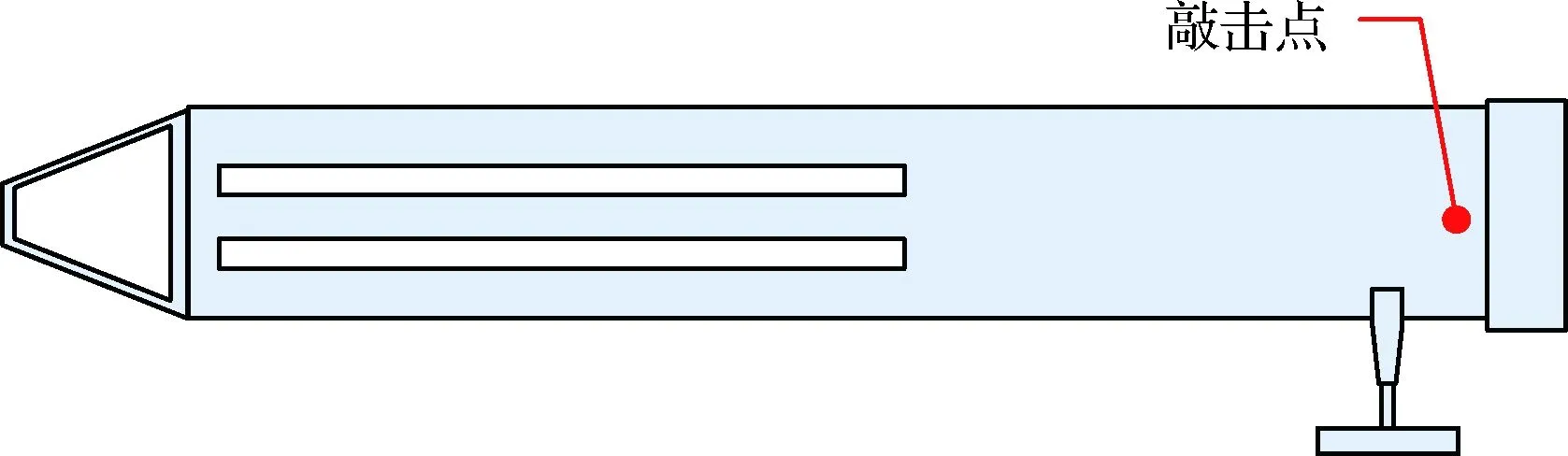
图11 试验敲击点Fig.11 Test knocking points

图12给出了根部力矩传感器测量结果，分析试验结果可知，敲击挠性板端部主要激发了第1阶模态，第1阶模态频率为ω1=0.2731 Hz，第2阶模态频率为ω2=2.5790 Hz。从表4可以看出实测值略小于有限元分析值，这是由于挠性板收到摩擦力、风阻还有其上管路的影响。

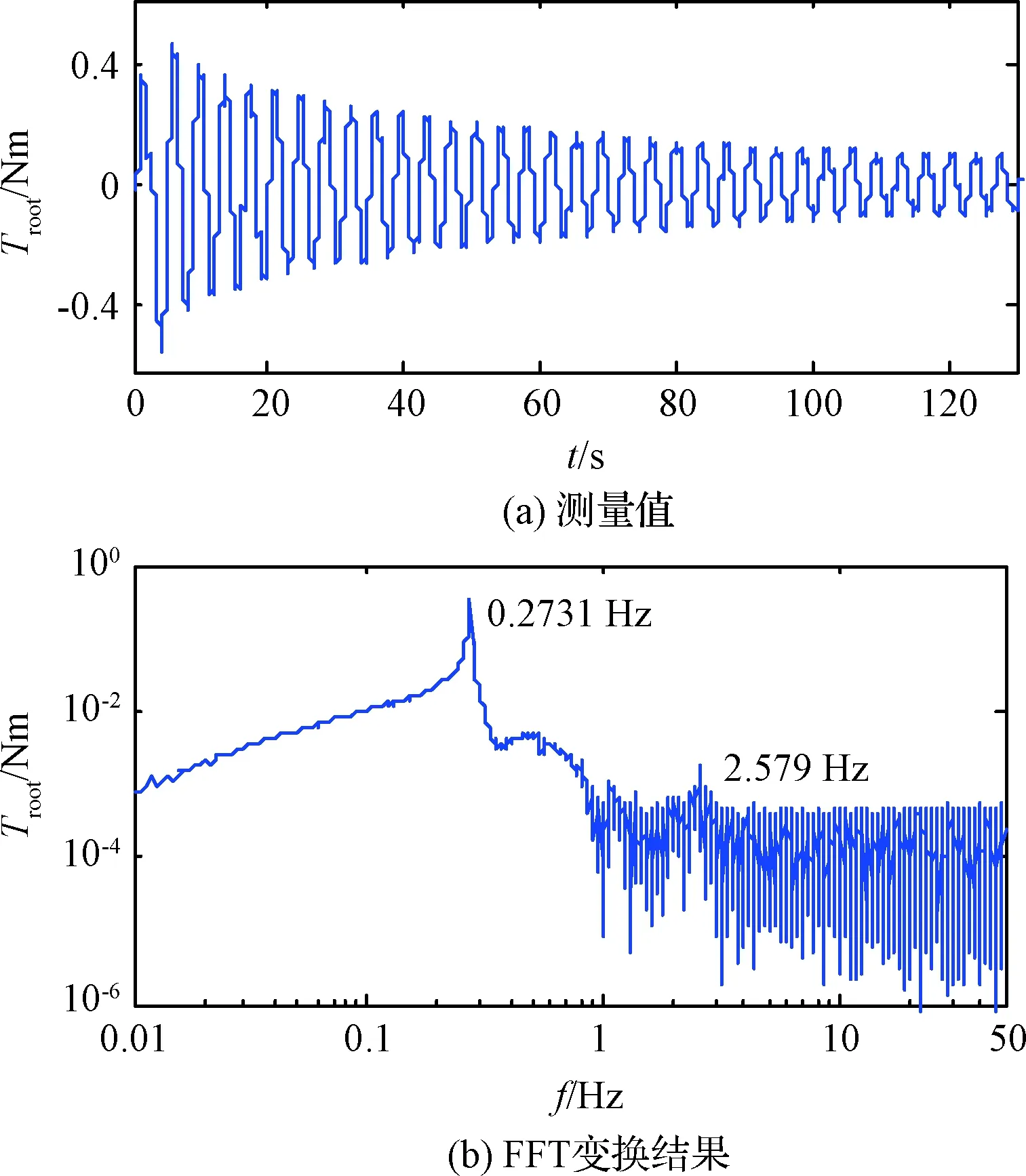
图12 悬臂状态下敲击点1力矩传感器测量结果Fig.12 Torque sensor’s measurement results with point 1 knocked under cantilever state

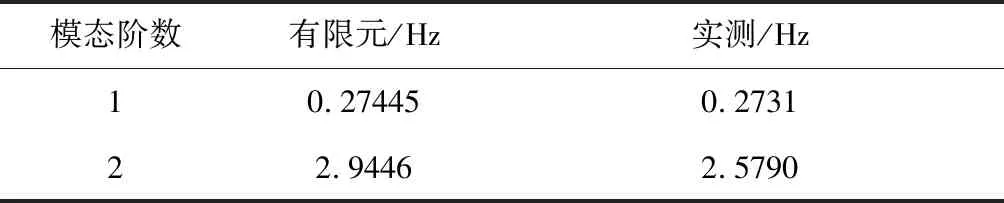
模态阶数有限元/Hz实测/Hz10.274450.273122.94462.5790

3.2 非约束模态频率测试

同时打开中心刚体的气足和挠性板端部支撑气足的供气，此时中心刚体与挠性板构成的刚柔耦合系统处于无约束状态，设置与图11相同的敲击点，对挠性结构进行敲击，测量自然振动。图13给出了力矩传感器测量值和FFT变换结果，表5给出了仿真计算和试验测试的非约束模态频率，分析试验结果：1)第1阶和第2阶模态频率均略低于有限元计算值，但误差不大；2)第1阶模态被激发的幅值远大于第2阶模态幅值，2阶以上的模态没有被激发。

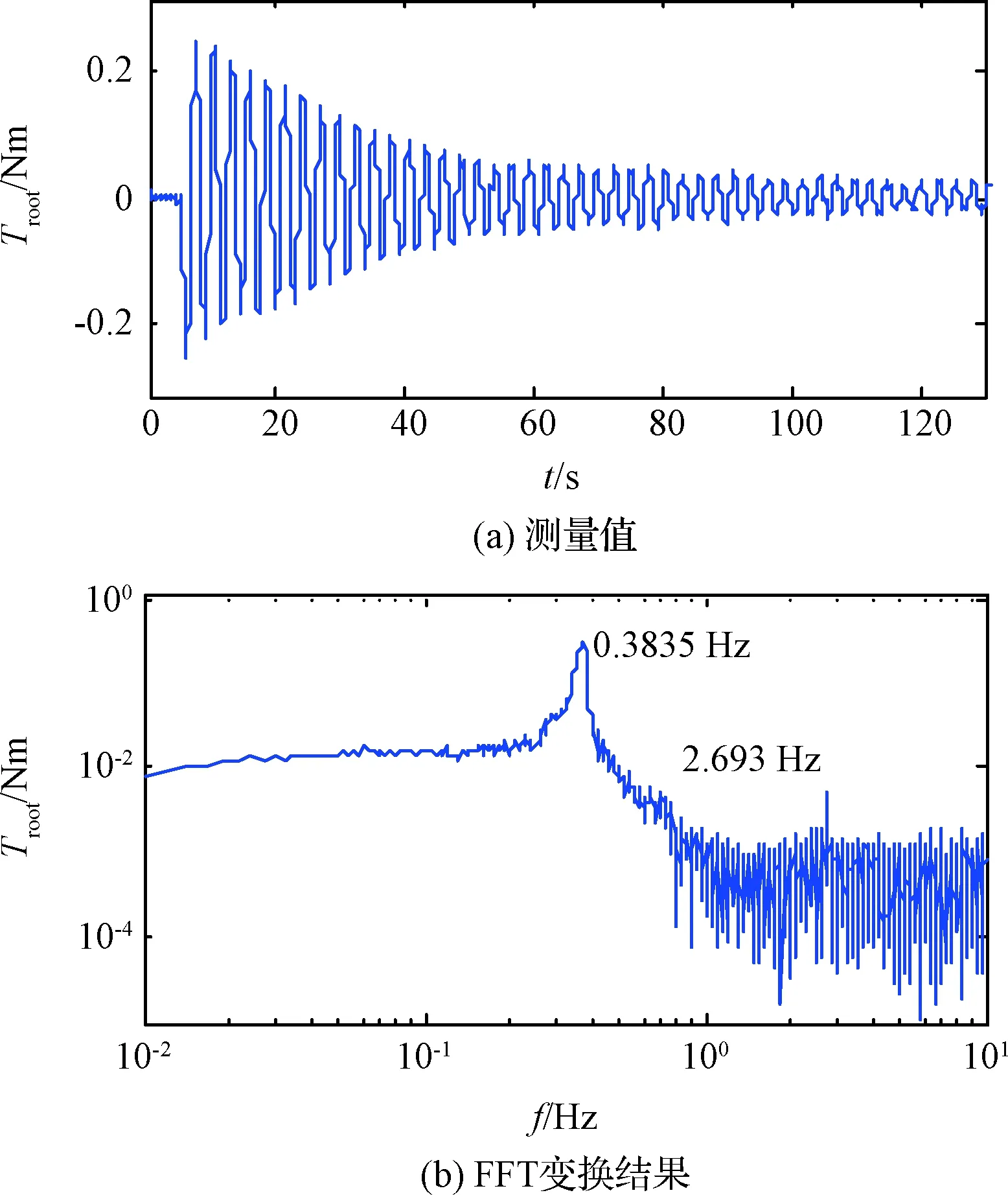
图13 无约束状态下敲击点2力矩传感器测量结果Fig.13 Torque sensor’s measurement results with point 2 knocked under unconstrained state

模态阶数有限元/Hz实测/Hz10.38400.383522.99432.693

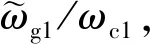
表6 非约束模态频率与悬臂模态频率的比值Table 6 Ratios of unconstrained modal frequencies and cantilever frequencies

由表6可知,试验结果与有限元计算结果、理论计算结果均比较一致，验证了全局模态动力学模型的准确性。

4 结 论

本文针对小中心刚体-单侧大挠性结构构型的航天器，通过定义广义全局模态振型提出了一种全局模态动力学模型，采用统一形式描述整体刚体运动和整体挠性变形。结合瑞利瑞兹法分析了非约束模态频率随着质量比和惯量比的变化情况，通过仿真、试验两种方式校验了所建立的全局模态动力学模型的准确性。结果说明全局模态动力学模型能够比较准确地描述非约束模态频率和模态振型，第一阶模态频率的最大误差为0.003 Hz，前六阶归一化模态振型计算最大误差为2.2%；通过与有限元模型比对，理论模型能够比较准确地描述动态响应，端部横向位移的最大误差为2.6%；基于气浮平台构建了试验系统，测量得到的非约束模态频率与悬臂模态频率的比值，理论模型、有限元仿真和物理试验结果均比较接近，说明理论模型准确描述了非约束模态频率随刚柔耦合特性变化的规律。