一种高超星图高精度半盲复原算法
2019-05-09李嘉兴杨照华刘玉双
杨 博,李嘉兴,杨照华,刘玉双
(1. 北京航空航天大学宇航学院,北京 100191;2. 北京航空航天大学仪器科学与光电工程学院,北京 100191; 3. 北京机电工程总体设计部,北京 100854)
0 引 言
高超声速飞行器近些年来不断朝着射程更远、精度更高的方向发展[1],其导航技术是重要的研究课题之一。目前国外的高超声速飞行器以GPS和惯性组合导航为主,而GPS具备的“三定一弱”(特定信标以特定频率发播特定格式的导航电文,导航信号微弱)特性再加上军事用途的约束,因此,探索适合于军用的自主导航技术成为了目前我国对该领域攻关研究的主要方向。天文导航是一种完全的自主导航方法,将其与惯性组合导航在特性上取长补短大大提高了惯性系统的精度和适应度。而将其应用于高超声速飞行器上仍处于研究阶段,气动光学效应是首当其冲的问题。飞行器周围的大气被加热,流场发生巨大改变,产生激波、附面层等复杂流场,光线通过湍流后致使星图产生偏移、抖动和模糊等负面效果[1],严重影响导航能力。对此类问题的研究通常分为两个步骤:首先研究高超声速飞行器周围高速流场的气动光学效应,然后对湍流和运动模糊星图进行补偿算法研究。
当前研究高速流场中星光气动光学效应的方法主要是通过数值模拟流场或实验测量真实流场的方式进行。数值模拟的方法通过几何光学、物理光学、统计光学的方法模拟光线穿过高速流场后的波前;而实验测量的方法则是直接测量穿过真实流场后的光线波前数据,再由波前计算出点扩散函数,进而分析因流场带来的光线偏折、像模糊等影响。例如Pond和Sutton[2]采用标准k-ε湍流模型对三维凸台周围的流场建立了数值仿真,利用相位差、斯特列尔比等参数对气动光学效应进行了评价;Gao等[3]利用流场可视化方法重构气体密度场,对超声速湍流边界层的气动光学效应进行了时间演化方面的研究。
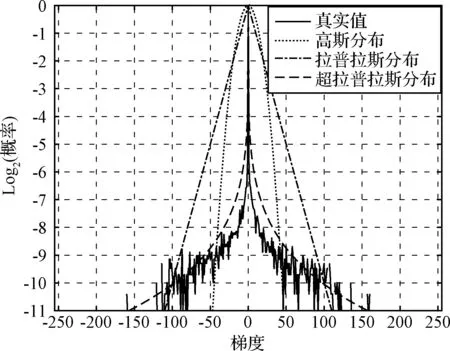
近几年图像复原技术作为一种解决高超声速飞行器气动光学效应问题的方法得到相当的重视。洪汉玉等[4]提出了一系列针对红外图像的气动光学复原算法,主要研究了基于极大似然估计准则的正则化复原算法,文献[4]提出了针对图像与点扩散函数特点的非线性各向异性正则化函数,文献[5]提出了基于泊松模型的多帧图像复原算法。正则化复原方法近年来在国际上发展迅速,Fergus等[6]提出基于变分贝叶斯的图像盲复原方法,Krishnan和Fergus[7]用超拉普拉斯分布来拟合图像梯度的重尾分布,Ohkoshi等[8]提出结合全变差模型和Shock滤波器的盲复原算法,Pan等[9]提出基于暗通道稀疏先验的盲复原算法。这些复原算法的研究思路主要是针对灰度、梯度、模糊核等特征的分布特性设计正则函数,通过最优化求解得到清晰图像。
上述的正则化复原算法研究对象均以自然图像为主,缺乏针对星图的研究。同时图像盲复原算法的关键是要根据图像丰富的边缘信息估计出准确的模糊核。对于高超流场影响下的星图基本失去了边缘信息,因而利用一般方法是无法建立准确的模糊核用于高精度复原。为此本文针对高超星图特点提出一种利用先验知识提取准确模糊核建立的半盲复原算法,并进行了计算机半物理仿真校验,获得了理想的结果,为高超声速飞行器利用星光进行自主导航提供了理论依据。
1 高超湍流场的运动星图模糊核
基于高超湍流的大涡模拟流场数据,利用几何光学和物理光学,统计计算湍流场影响下的星图模糊核;并根据湍流叠加模型,引入随机运动模糊,建立具有气动光学效应和运动模糊的高超湍流的运动模糊核。
1.1 高超湍流的大涡模拟
星光经过激波、湍流边界层、弹体冷却层等之后,光学窗口外复杂高速流场产生的气动光学效应使星敏感器接收的图像存在严重的偏移、抖动和模糊。由激波引起的稳定偏折可由文献[1]中的经验公式计算。而本文只重点研究湍流模糊与运动模糊问题。
为了尽可能准确地揭示高超湍流场中星光光线传播的特性,使用大涡模型对湍流流场进行模拟,其流场密度分布如图1所示。
1.2 湍流场中的星光传输效应
基于上述大涡流场模拟结果,利用物理光学方法计算流场的光学传输效应。根据Gladstone-Dale定律将密度分布转换为折射率分布,利用光线追击法计算平面波的光程差(Optical path difference,OPD),如图2所示。
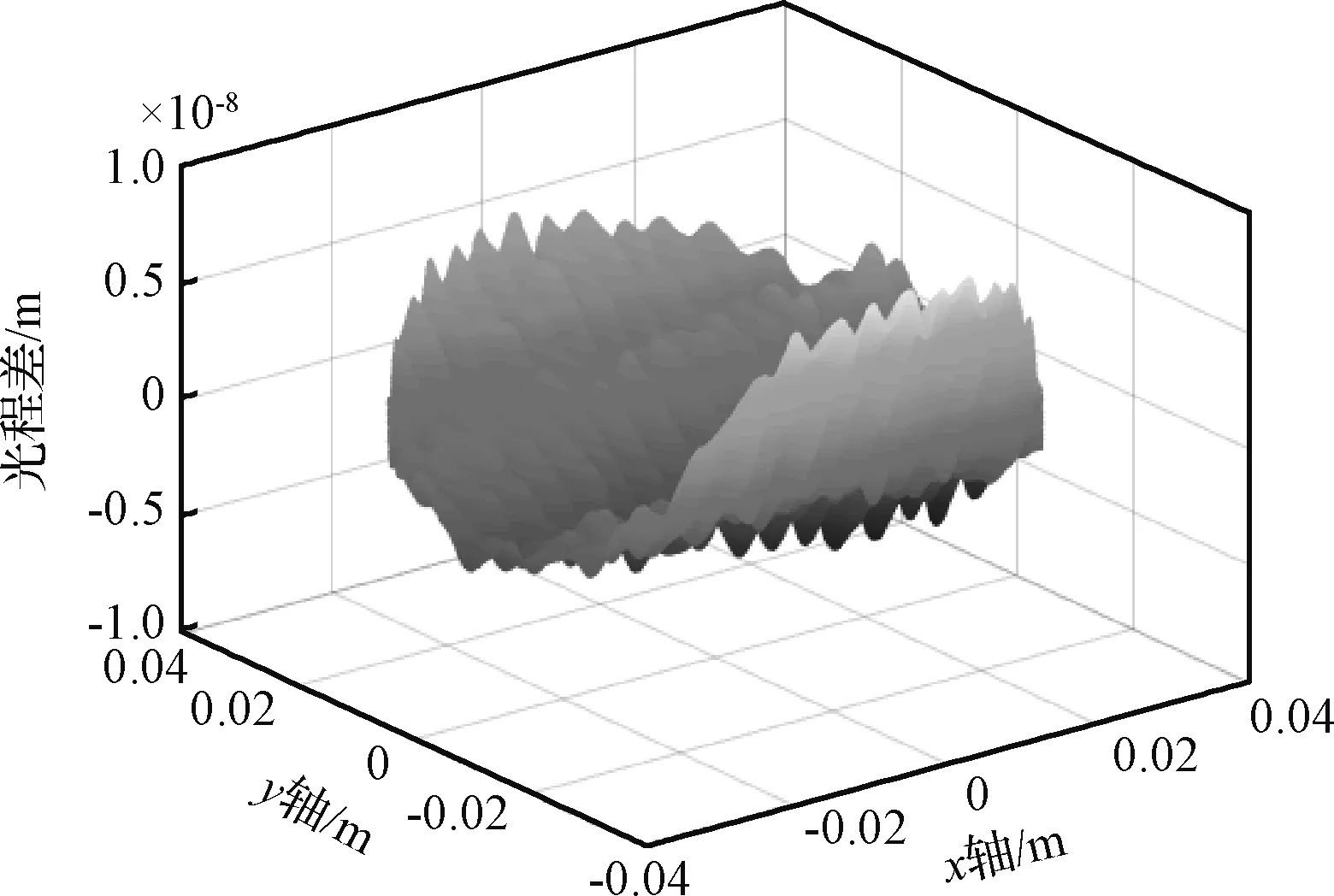
图2 光程差示意图Fig.2 Optical path difference
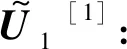
w(x,y)=kΔOPD(x,y)
(1)
(2)
式中:x和y为像面坐标系中的横纵坐标,k=2π/λ,λ为星光波长,a为波面的振幅分布,j为虚数单位。
1.3 湍流影响的退化星图建模
(3)
(4)

(5)
(6)
式中:F(·)表示快速傅里叶变换,上标*表示复共轭,∘ 表示矩阵点乘(即对应位置元素相乘)。
设高超声速飞行器飞行过程中光轴抖动产生运动模糊效应,并有随机运动模糊的模糊核为hM,将其与高超湍流模糊核卷积即可得到高超湍流场运动模糊核,如图3所示。
h=hH⊗hM
(7)
其中,⊗为空间卷积运算。根据湍流冻结理论,认为短曝光的湍流退化图像的模糊核线性位移不变,可将湍流退化过程简单表示为目标图像与模糊核的卷积过程,同时考虑噪声有:
g(x,y)=f(x,y)⊗h(x,y)+n(x,y)
(8)
式中:g(x,y)为退化图像,f(x,y)为清晰的目标图像,n(x,y)为加性噪声。为方便表示,下文将写作g,f,h,n。
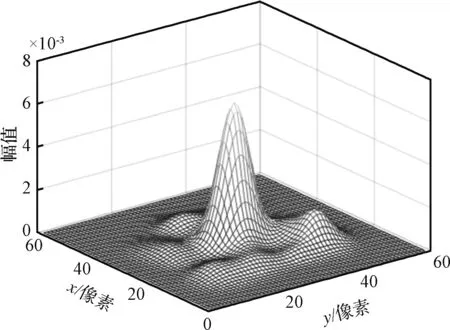
图3 高超湍流运动模糊核Fig.3 Kernel of hypersonic turbulence and motion
2 高超湍流星图的复原预处理
对星光通过大涡模拟的湍流场时,受到衰减后的星图点扩散函数图3,提出运用三种复原预处理技术:低通去噪、星点粗提取、模糊核估计,以此提高模糊核的估计准确度,并保证获得最佳的复原效果。
2.1 低通滤波

图4 大涡模拟流场星图Fig.4 Astronomical image simulation from LES
由式(8)随机生成模拟流场星图,如图4所示。从图4可以看出,星点有大量的分布信息淹没于随机噪声中,直接采用阈值分割,会丢失过多的星点能量,造成星点亮度降低质心提取不准确,甚至可能将抹去低亮度星点的全部信息,使得星点跟踪失败。而从图3可以看出,湍流模糊核分布比较平滑,信息变化缓慢,说明模糊图像具有较强的低频特性。因此采用参数适当的高斯低通滤波器先对原始星图进行滤波处理,得到的去噪图像如图5所示。
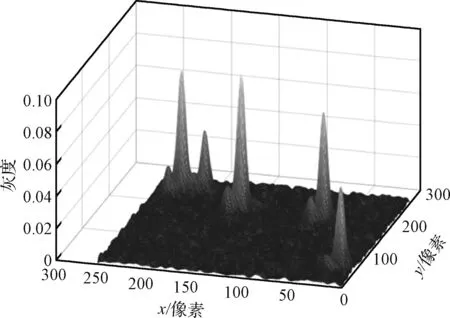
图5 低通滤波后的高超星图Fig.5 Image after LPF
比较图5与图4可以看出,经过合适的低通滤波器预先处理,图像去除了大量高频噪声,而大部分星点信息被分离保留下来。但由图5可知,星点能量处于分散状态,并且邻星之间存在能量叠加区域(左上部的两颗星),为了获得较高的质心提取精度,需对图像进行复原,集中星点能量。
分割域值选取,是通过精确地分析统计噪声的分布P,得到噪声的均值与方差,同时根据大量滤波后星图灰度的统计特性,设计灰度分布拟合函数:
(9)


图6 灰度分布拟合示意图Fig.6 Fitting of gray distribution
2.2 星点初提取

图7 星点提取方法对比Fig.7 Comparison of star point extraction methods
从图7中上下两个白色方框内的分割结果可以分别看出,改进方法在平滑多峰和避免重叠方面的效果,利用此提取方法可以大大避免由气动光学效应造成的星点提取错误。尽管如此,初步提取的星点坐标并非是由该星点的全部图像信息提供,因而坐标准确度较低,并且能量较弱或相邻很近的星可能会无法提取。
2.3 模糊核提取
天文图像的模糊核提取与光学系统点扩散函数测量问题中的点脉冲法十分相近,但在气动光学作用下,需解决模糊核重叠、图像边界处不完整及成像噪声等问题。
假设星图中有M颗星,坐标是(xm,ym),(m=1,2,…,M),能量为Im的星点图像为Imδ(x-xm,y-ym),式中δ(x,y)为脉冲函数,则原始星图可表示为:
(10)
经过点扩散函数h的退化,并加入噪声后的退化图像可表示为:
g(x,y)=f⊗h+G(μn,σn)=
(11)

假设1. 阈值分割阶段可以估计出准确的噪声均值。
当假设1成立时,在退化图像中去除噪声均值,即g-μn后,边界延拓L/2,以(xm,ym)为中心,提取L×L的图像为:
Ωm(x,y)=Imh(x,y)+G(0,σn)+
(12)
式中:L为估计模糊核的支持域边长,Δxmm′=xm′-xm,Δymm′=ym′-ym,D(sm,sm′)为m星到m′星之间的距离。
由式(12)可知,Ωm(x,y)中包含m星对应的点扩散函数h、零均值噪声以及重叠的其他星的干扰能量,去除重叠区域干扰的处理如下:
将Ωm(x,y)写为极坐标形式Ωm(φ,r),在剔除不可用的区域之前,设保留区间为φn=U=[0,2π)。
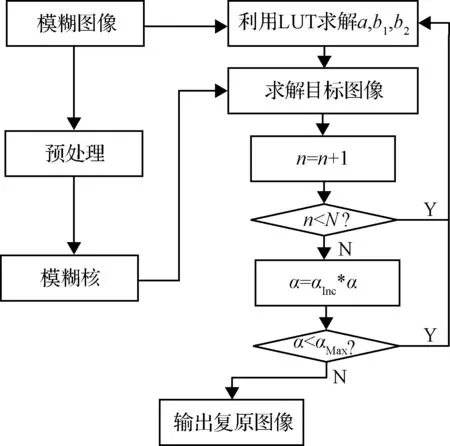
1)剔除Ωm中与边界重叠的区域,如图8(a)所示,其中虚线为扩展前的边界:如果(xm,ym)与某边界b的间距Db(sm) θmb=arccos(2Db(sm)/L-1) (13) 更新保留区间为: φm∶=φm (14) 式中:“”表示集合作差。剔除后的剩余区域都不与边界重叠。 图8 半圆心角示意图Fig.8 Semi central angle (15) 3)更新保留区间为: φm∶=φm (16) 将与边界重叠和模糊重叠的圆心角区域剔除后,Ωm可更新为: (17) 假设2. 利用式(17)成功剔除了m星与其它星的模糊重叠区域。 当假设2成立时,m星的能量近似为: (18) 并以其作为归一化系数,归一化Ωm: (19) (20) 加权融合后即得到模糊核: (21) (22) 式(12)在满足假设2的条件下,可改写为: (23) 期望和方差为: (24) (25) 将式(20)、(23)代入式(21),可得: (26) 则期望和方差为: E(hp(r,φ))=h(r,φ) (27) (28) 在满足假设1和假设2的条件下,式(27)表明模糊核先验估计hp是退化真实模糊核h的无偏估计。式(28)表明融合后的方差一定小于每颗星先验区域内的方差: (29) 式(29)表明融合过程能降低其中的噪声方差,起到降噪作用。 由式(28)可得: (30) 基于提取并融合的模糊核,并将其用于非盲复原这一过程称为半盲复原。一般正则化技术具有一定的快速性及模糊核估计误差鲁棒性。 分析目标的先验知识构造正则化项,用以约束最优化求解过程。将清晰的星图的灰度分布统计经对称化处理后如图9所示。 图9 星图灰度分布示意图Fig.9 Gray distribution of astronomical image 图10 星图梯度分布示意图Fig.10 Gradient distribution of astronomical image (31) (32) 交替计算f与辅助变量,其中f可由下式计算: (33) 式中:F-1(·)为快速傅里叶逆变换,δx和δy分别为水平和垂直一阶差分算子。由式(33)更新f后,对其进行半正定约束: (34) 同时,辅助变量的子问题表示为: (35) 式中:w∈{a,b1,b2},v∈{f,δxf,δyf}。采用文献[10]给出的LUT算法快速求解。图11为总体复原算法流程图,记为算法1。 图11 复原算法流程图Fig.11 Restoration algorithm 在模糊核提取过程中,剔除每颗星与边界、其他星重叠的区域后,剩余部分可由图12所示,白色框中的部分即为应用于融合模糊核的图像。 图12 模糊核融合区域示意图Fig.12 Fusion area of kernel 利用算法1和对比算法分别对湍流模糊星图进行复原,估计模糊核和复原图像分别如图13和图14所示。对比可以看出,CLSF算法对模糊核估计准确度的要求较高,很难复原出质量好的图像。Krishnan等[11]的算法使用L1先验,平滑度较高,可以抑制绝大多数噪声,但同时复原的星点较粗,能量不够集中,可能会使相邻星点融为一体,难以区分相邻的两颗星。Pan等[12]的算法使用L0先验,虽然可以得到更细致的星点,但过度保留了图像梯度,使复原图像中依然存在大量高频噪声,易使星点误识别率高。算法1中使用的Lp先验模型,效果介于L1与L0之间,其既可抑制噪声,同时也集中能量,提高了星点质心提取精度。 图13 模糊核对比Fig.13 Comparison of kernel 图14 复原星图对比Fig.14 Comparison of deblurred image 表1 不同复原算法的平均PSNR对比Table 1 Comparison of mean PSNR between different algorithm 如表2所示是对复原后的星图进行星点质心提取的精度比较。由复原图像计算识别出的星点质心坐标,并与原始星点坐标数据进行对比,将坐标误差小于2个像素记为识别正确,其个数占总星数的比例为识别正确率。同时将正确识别的星点坐标与真实坐标进行对比,统计二者的平均误差角距。从表2可以看出,算法1的星点识别最精确,从而印证了此方法对模糊核的估计更准确,并且复原精度更高,使得复原图像更接近实际图像,在提取星点时所受到的噪声、模糊核多峰结构、模糊重叠等影响因素更小,有助于提高识别精度。 表2 星点识别精度对比Table 2 Comparison of star recognition accuracy 采用文献[13]给出的误差率作为评价模糊核的估计准确度,对不同算法统计积累误差率绘制曲线如图15所示。图中曲线越高说明模糊核估计得越准确,因此可以看出该算法1的模糊核估计准确度最高。例如在误差率1.2的指标下,对比算法分别有50%和25%的复原图像达到要求,而算法1有超过80%达到要求,由此可以明显看出该算法的优越性。 图16为所有复原图像的累积误差率与星点质心识别正确率的关系示意图。从图16可以看出,随着误差率的积累,对较差复原效果的容忍度越高,星点识别正确率自然随之降低。在实际使用时可以根据不同识别正确率的任务需求,结合图16和图15得到不同算法的占比成功率,具体示例如表3所示。 图15 积累误差率示意图Fig.15 Accumulated error rate 图16 积累误差率与识别精度的关系示意图Fig.16 Relationship between accumulated error rate and recognition accuracy 识别正确率/%占比成功率/%文献[11]文献[12]算法19026253803446770502484 由表3的对比分析可知,在不同识别正确率需求下,算法1满足任务的复原图像占比均明显高于对比算法,此对比进一步验证了该算法对能有效提高星点识别能力。综合上述对比可以看出,与传统盲复原算法中仅利用图像边缘信息估计模糊核并复原的思想相比,针对高超湍流模糊复原问题,算法1能够有效结合星图特点及高超模糊核特点从而提取出更精确的模糊核,并且利用星图灰度分布的特点使得复原效果达到最佳,因此星点质心提取的正确率和精度更高。 针对高超声速飞行器在平流层使用天文导航受气动光学及运动模糊干扰的关键问题,本文结合气动光学效应对星图复原算法进行深入研究,填补了气动光学研究至复原算法之间的空白,得到以下结论:1)基于区域剔除与融合操作,模糊核提取方法对高超湍流模糊星图模糊核的估计精度高于其他盲复原算法。2)基于星图灰度与梯度的稀疏特性,算法1对高超湍流模糊星图的复原精度高于其他复原算法。3)经算法1复原后的星点识别正确率可达78%,误差角距低至0.0249°。因此若将本文提出的复原算法应用于高超声速飞行器的天文导航领域,可大幅提升导航适应能力及导航精度。同时可为高超声速飞行器星图复原的深入研究提供思路。



2.4 模糊核特性分析

3 高超星图正则化非盲复原


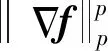


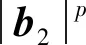
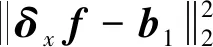
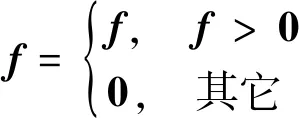
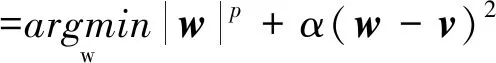
4 仿真校验
4.1 仿真条件

4.2 仿真结果










5 结 论
