非线性干扰观测器补偿的四旋翼飞行器模糊滑模控制

赵嘉伟，张宏立，李新凯

(新疆大学 电气工程学院，新疆维吾尔自治区 乌鲁木齐 830047)

四旋翼飞行器作为微型飞行器的一个分支，广泛应用于军事领域和民用领域.四旋翼飞行器体积小、造型简单、结构对称，具有空中机动、垂直起降和悬停的优点.在军事领域，四旋翼飞行器可用于低空侦察、目标打击、战场监视等；在民用领域，可用于农药喷洒、电力巡检、小区安防等.随着微型飞行器的应用和推广，四旋翼飞行器越来越受到关注.

四旋翼飞行器具有非线性、欠驱动的特点，存在外界未知扰动条件下的不易控制问题[1].传统PID(proportion integral derivative)算法在对四旋翼飞行器进行控制时，对扰动和耦合变量的反馈进行了简化[2]，能实现飞行轨迹的控制，但控制精度较低.非线性PID算法能弥补传统PID算法非线性状态反馈的缺陷，但实现条件严格[3].滑模控制(sliding mode control，简称SMC)算法能有效解决控制对象模型存在的非线性、欠驱动和强耦合问题[4-6].在外界扰动条件下，利用SMC算法能使对象有较好的性能，但控制器输出受到干扰时会出现抖振，滑模控制器的输出呈不稳定状态，且扰动上界的不确定会影响滑模控制器参数的选取.非线性干扰观测器能对控制器的输出进行补偿，可减小扰动[7]、提高控制精度[8-11].文献[12]针对四旋翼飞行器的姿态动力学模型，设计了非线性干扰观测器作用下的跟踪算法，可跟踪目标的期望轨迹.上述基于非线性干扰观测器的算法中，有的没有考虑模型的欠驱动性，有的非线性干扰观测器的非线性形式过于复杂、不易实现.笔者针对四旋翼飞行器非线性、欠驱动的特点，分析飞行器的飞行原理，考虑旋翼电机桨叶的受力，建立飞行器的动力学模型，提出非线性干扰观测器补偿的模糊滑模控制算法，解决滑模控制过程中因干扰而产生的抖振问题，使飞行器稳定飞行.

1 四旋翼飞行器的动力学模型

四旋翼飞行器具有十字型结构或X型均匀对称结构.相邻两电机的转速方向相反，用于抵消飞行过程产生的空气扭矩效应，通过调节分布在4轴外侧顶端电机的转速，实现力和力矩的变化，使飞行器实现不同运动形式和姿态.

四旋翼飞行器的飞行原理如图1所示，其中f1，f2，f3，f4为4个电机旋转产生的升力，Roll，Pitch，Yaw均为姿态角.保持1，3电机转速不变，改变2，4电机的转速，使f2和f4发生变化，能实现四旋翼飞行器的俯仰运动.同理，保持一侧轴对称两电机转速不变，改变其他两个电机的转速，亦能实现四旋翼飞行器其他的运动姿态.

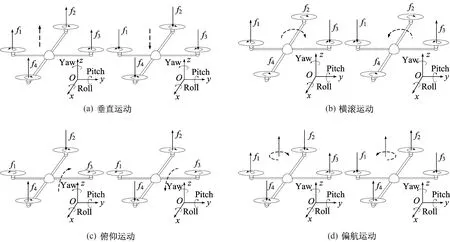
图1 四旋翼飞行器的飞行原理图

四旋翼飞行器从地面参考坐标系到运动坐标系的变换矩阵为

(1)

其中：φ,θ,ψ分别为俯仰角、横滚角、偏航角；Θ(φ,θ,ψ)为参考坐标系下姿态角.

角速度在参考坐标系下的变换矩阵为

(2)

被控对象应满足以下假设：

(1) 四旋翼飞行器为刚体结构，对称分布；

(2) 螺旋桨为刚体，转动时不发生形变.

根据牛顿定律和欧拉-拉格朗日方程，参考坐标系下的动力学方程为

(3)

其中：Ω为四旋翼飞行器在参考坐标下的角速度.

对于一般低速飞行来说，电机的力矩与转速满足如下关系

(4)

其中：bi为电机的转动系数，ωi为电机的转速.(4)式表明四旋翼飞行器的控制力矩与电机转速平方成正比，利用这一关系，对模型中的控制量进行设计.假设电机无时滞，基于桨叶的受力情况，结合(4)式，可得到控制量U和τ与电机转速的关系如下

(5)

其中：CT和CQ分别为旋翼的拉力系数和扭矩系数，ρ为旋翼工作环境的流体密度，A为桨叶的受风面积，r为旋转半径，d为电机与飞行器质心的距离.

设ωz,Δωz,Δωφ,Δωθ,Δωψ分别为飞行器在低速飞行时的悬停转速、垂直方向转速调节量、俯仰转速调节量、横滚转速调节量、偏航转速调节量，则 (5)式中的U可表达为如下形式

(6)

如果飞行器保持悬停状态，则有

(7)

(8)

将(6)～(8)式代入动力学方程(3)式，得到四旋翼飞行器动力学方程为

(9)

四旋翼飞行器的两个非完整约束为

(10)

约束的存在是四旋翼飞行器不能实现完整意义上6自由度运动的原因.

系统的欠驱动子系统、完整驱动子系统的动力学方程分别为

(11)

(12)

其中：x,y与φ,θ构成欠驱动子系统；z与ψ构成完整驱动子系统；ux,uy为欠驱动子系统在x,y处的输入；m为刚体质量；Ixx,Iyy,Izz为系统的转动惯量.

2 非线性干扰观测器补偿的模糊滑模控制算法

2.1 模糊滑模控制

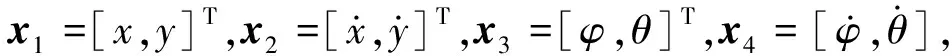
(13)

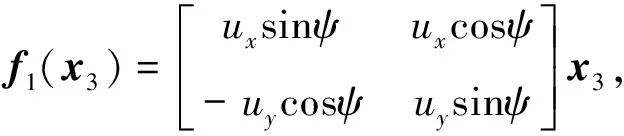
定义滑模面函数

s=c1e1+c2e2+c3e3+e4=

(14)

等效滑模控制项为

(15)

切换控制项为

(16)

其中:η为滑模面增益，δ为滑模可调参数.

等效滑模控制器的输出为u=ueq+us.为了消除抖振，应使切换项根据干扰的大小进行调整.当外界干扰较大时，提高切换项可在一定程度上克服干扰，消除滑模抖振；当外界干扰较小时，降低切换项能达到消除抖振的目的.FSMC控制律u=ueq+μ·us,其中μ=1为等效滑模控制，μ≠1为模糊滑模控制.根据干扰数值的大小改变μ值，降低滑模抖振，提高控制的准确性.

模糊化规则为

ifs(t) isNthenμisN；ifs(t) isZthenμisZ；ifs(t) isPthenμisP.

采用上述模糊化规则，能减少滑模抖振对控制器的输出产生影响，使控制器的输出更加稳定.

2.2 非线性干扰观测器

针对四旋翼飞行器控制系统动力学模型中的部分不确定和外界未知扰动难以估计的问题，为逼近外界扰动的实际值，提高控制精度，达到稳定控制，设计非线性干扰观测器(nolinear disturbance observer，简称NDO).假设姿态子系统的复合干扰为慢时变干扰，则非线性干扰观测器有如下形式[13]

(17)

其中：

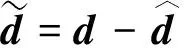
2.3 非线性干扰观测器补偿的模糊滑模控制算法

在NDO误差收敛的基础上，FSMC控制律可表达为

(18)

其中：

Lyapunov函数的表达式为

(19)

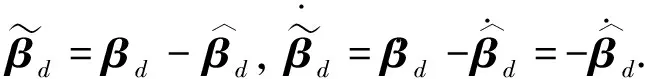
对(19)式求导，得

(20)

其中：E=(e1,e2,e3).

非线性干扰观测器补偿的模糊滑模控制框图如图2所示.由图2可知，在实际飞行控制中，外界扰动变化时，NDO能将观测误差传给FSMC控制器，控制器按扰动变化调节输出，在扰动变化频率加大或扰动突变时，控制器可使输出保持稳定，避免滑模抖振给系统带来不良影响.基于图2中的非线性干扰观测器补偿的模糊滑模控制策略，笔者提出非线性干扰观测器补偿的四旋翼飞行器模糊滑模控制算法.

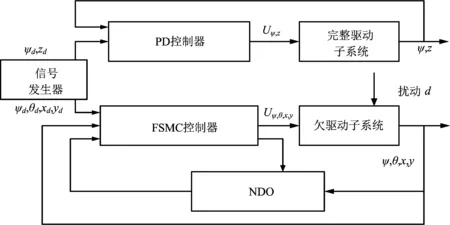
图2 非线性干扰观测器补偿的模糊滑模控制框图

3 仿真结果

初始位置为[0,0,0]T,初始姿态为[0,0,0]T,期望位置为[3,4,5]T,期望姿态为[0,0,0.1]T.

欠驱动子系统的模糊滑模控制参数设置如下

m=0.8 kg,Ixx=Iyy=0.25 kg·m-2,Izz=0.05 kg·m-2,CT=0.004 7，

CQ=0.000 228 ,ρ=1.184 kg·m-3,A=0.071 m2,r=0.15 m,d=0.35 m，

c11=4,c12=15,c13=10,c21=6,c22=12,c23=4,λ=1,δ=0.1,γ=2.

模糊滑模参数μ的隶属度函数如图3所示.

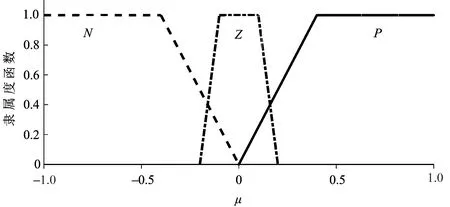
图3 模糊滑模控制隶属度函数

非线性干扰观测器设计为如下形式

其中：k1=0.1,k2=0.1,k3=0.01,k4=0.01.

将干扰d1,d2取为慢时变干扰，其表达式为

图4为周期扰动下的模糊滑模控制器输出.由图4可知，在SMC作用下，扰动值周期变化导致抖振，且抖振的上下界差值很大，不利于四旋翼飞行器的稳定控制.而在FSMC作用下，因周期性误差造成的控制器输出抖振的现象明显改善，控制器的输出趋于稳定.

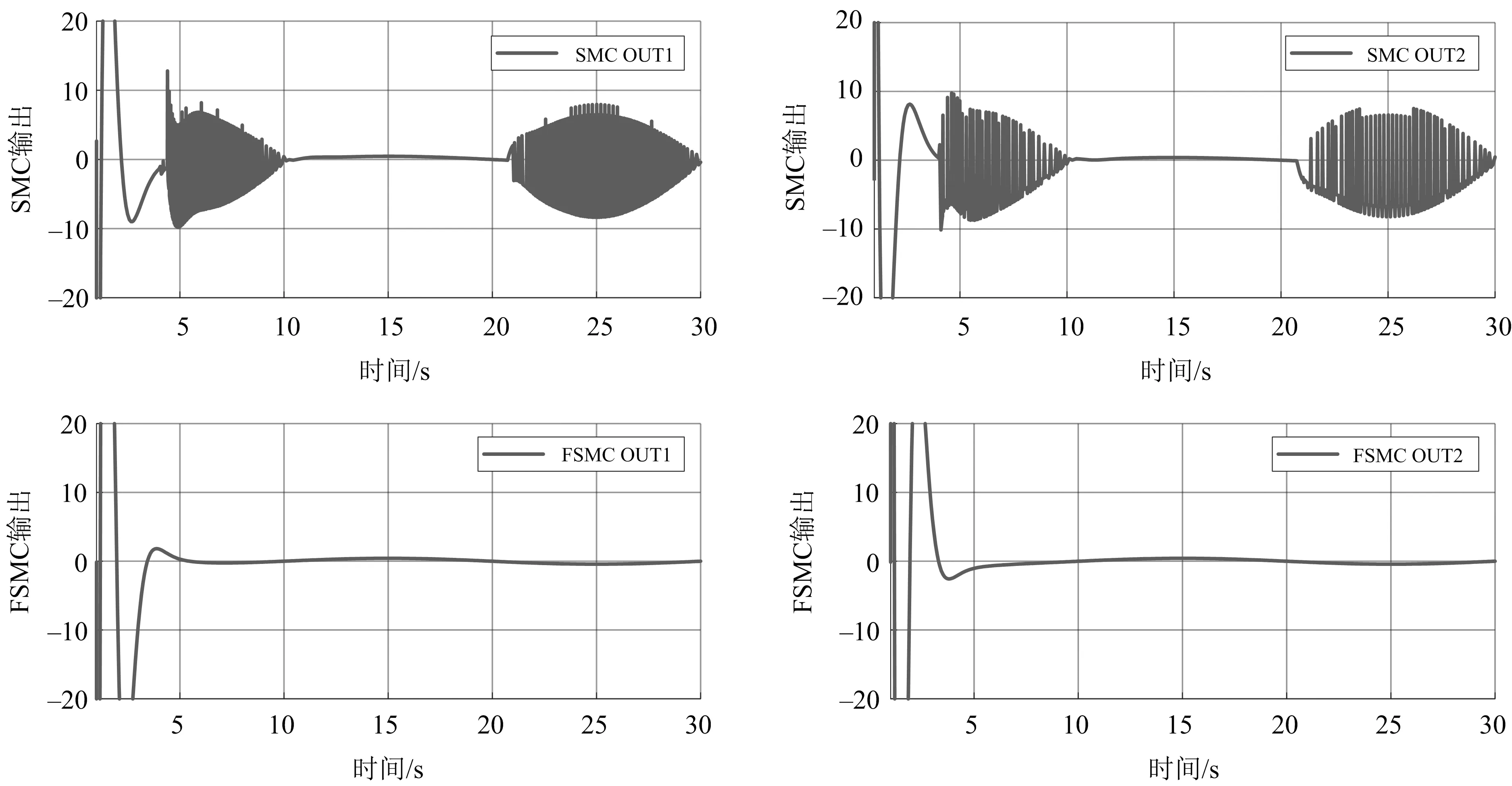
图4 周期扰动下的模糊滑模控制器输出

图5为周期扰动下的四旋翼飞行器欠驱动子系统的姿态和位置，其中φd,θd和xd,yd分别对应姿态和位置的期望轨迹.由图5可知，PID和SMC算法对扰动的抑制不明显，对干扰的补偿能力较弱，与期望轨迹间有周期性误差，表明PID与SMC算法在应对周期扰动时无法实现很好的稳定控制.使用该文算法时，四旋翼飞行器飞行呈现稳定状态，FSMC控制器对外界未知扰动进行补偿，使姿态和位置受扰动的影响降低，近似收敛于期望轨迹，这表明该文算法在干扰条件下能实现四旋翼飞行器的稳定控制.

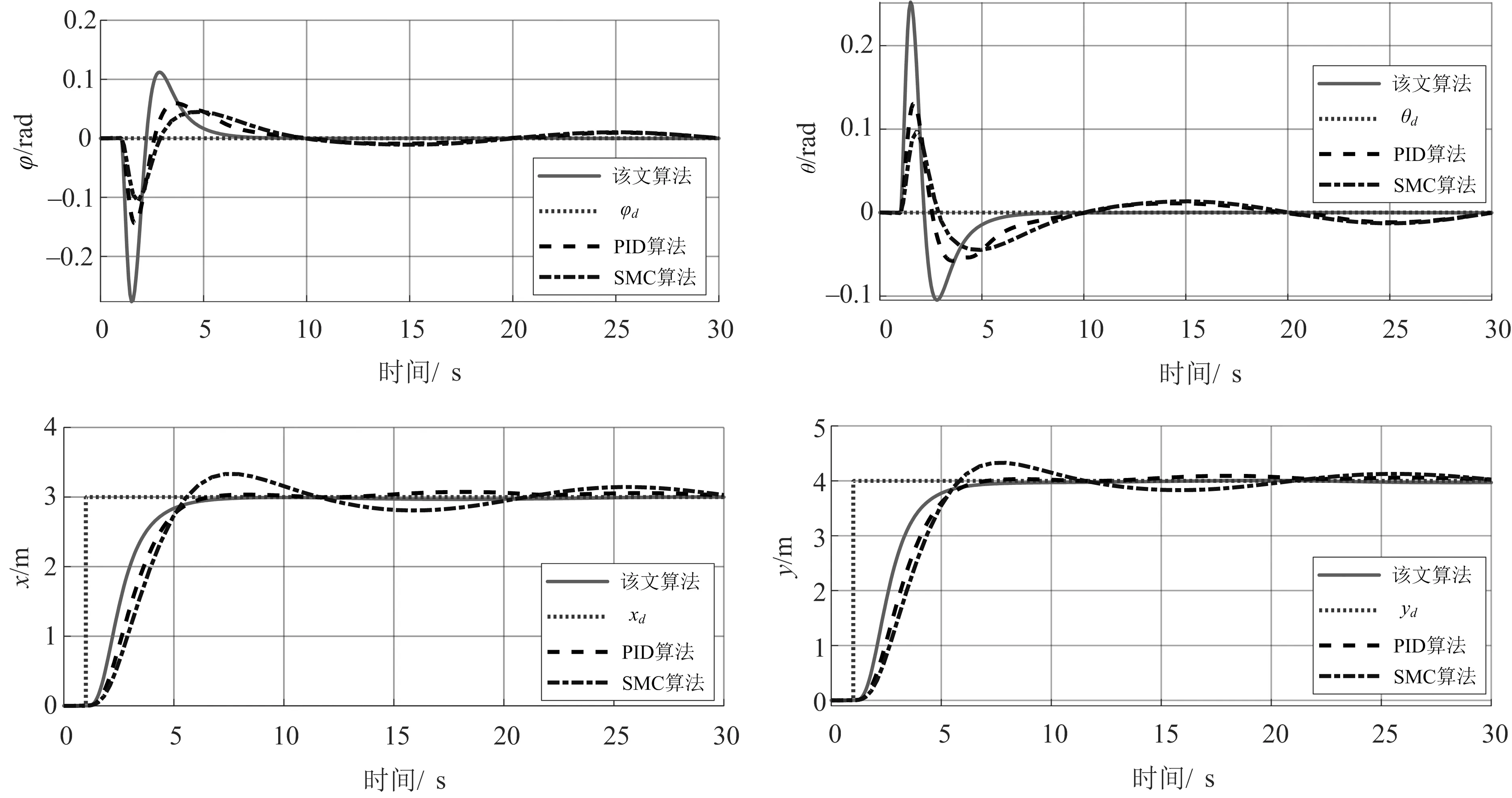
图5 周期扰动下的四旋翼飞行器欠驱动子系统的姿态和位置

4 结束语

笔者针对四旋翼飞行器扰动条件下飞行控制问题，建立桨叶受力条件下的四旋翼飞行器动力学模型，提出非线性干扰观测器补偿的模糊滑模控制算法.仿真结果表明该算法实现稳定控制的同时，解决了SMC中的抖振问题，且具有良好的鲁棒性.