Duffing振动系统的全局吸引子研究

冯进钤,刘亚妮，王迎宵，李玉婷

(西安工程大学 理学院，陕西 西安 710048)

Duffing振动系统作为非线性系统的经典模型，其全局动力学的研究一直是学者关注的热点. 胞映射方法作为一种研究非线性系统全局动力学的有效数值方法，最先由Hsu[1]在20 世纪80 年代初提出,随后得到了广泛发展，包括简单胞映射[2]、插值胞映射[3-4]、广义胞映射[5]、胞参照点映射[6-7]、图胞映射等[8-12]. 胞映射方法的生成最常用的方法是采样点方法. 胞映射方法不仅可以从空间范围角度呈现系统的全局结构，包括共存吸引子、吸引盆和吸引盆边界等结构，而且能捕捉到系统的非吸引不变集，如鞍型不动点、周期鞍和混沌鞍等. 该方法的优点是数值轨道都是根据原系统来生成的，但缺点是需要解决大量的常微分方程初值问题的模拟，导致计算效率较低.

鉴于此，论文基于摄动法的思想，将每个小胞中的采用点看作是该胞中心点的初始扰动，讨论了每个胞中不同采用点作为初始点的常微分方程的快速求解，并将其应用到图胞映射方法中，大大提高了计算效率. 与文献[13]中多项式逼近算法相比，论文方法公式推导简单，便于程序实现. 对于随机动力系统而言，高斯短时截断方法被广泛采用[14-21]，大大提高了图胞映射算法的效率. 但该方法受限于高斯白噪声激励下的随机动力系统. 论文方法更具一般性，适用于更一般的Markov过程驱动下随机动力系统. 论文以典型Duffing振动系统为应用实例，分析了系统全局吸引子的空间结构, 与已有结果比较，验证了该方法的有效性.

1 轨道摄动(orbit perturbation,简称OP)积分法

考虑如下常微分方程初值问题描述的非线性系统

dx/dt=f(t,x),x(t0)=x0，

(1)

其中：t∈R是独立时间变量；向量x∈D⊂Rn表示系统的运动状态，满足Lipschitz条件；向量函数f(t,x)∈Rn充分光滑，描述系统的向量场.

对于系统(1)，当有非线性项存在时，其精确解通常是无法得到的，可借助数值积分法来求解.常用的数值方法有泰勒级数法、Runge-Kutta(RK)单步法、Adams-Bashforth(AB)多步法.

首先将积分区间[t0,t0+T]等分为N等分，分点为tk=t0+kh,k=0,1,…,N,h=T/N为积分步长. 设φ(x0,t0;t)为向量场f(t,x)产生的流，x(tk)和xk分别为系统(1)在tk时刻的准确值和近似值，记x(tk)=φ(x0,t0;tk).4阶显式积分公式对应的局部截断误差可以表示为

εk+1=h5Φ(tk,x(tk))+O(h6)，

(2)

其中：函数Φ(t,x)=λd(5)x/dt(5)为局部误差函数的主导项，λ为常数.

由(2)式可以看到，缩小步长h和减小Φ都可以提高精度. 当固定精度εk+1时，主导项h5Φ(tk,x(tk))中步长h与函数Φ成反比，即当Φ越小时，可以采用较大的步长h，同样可以获得相同的精度；另一方面，采用较低精度的数值积分法也可得到较高精度的解.

基于上述讨论，论文介绍轨道摄动法. 假设对于给定的初值x0，系统(1)存在唯一解x(0)(t)=φ(x0,t0;t)，称为参考轨道. 由方程(1)知

dx(0)/dt=f(t,x(0)),x(0)(t0)=x0.

(3)

对参考轨道的初值x0做微小的扰动

得到的唯一解为

称为目标轨道，则

(4)

其中

称为摄动轨道.

由方程(3)和(4)可得其满足如下微分方程

(5)

其中：g(t,δx)=f(t,x(0)+δx)-f(t,x(0)).

(6)

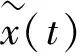
另外，当需要计算大量的目标轨道时，都可以共用一条参考轨道，利用大步长数值积分法求解方程(5)，然后借助(6)式即可快速得到目标轨道的数值解. 仅损失存储参考轨道的内存，即可获得运算速度的大幅提升. 该算法可以推广到一般的非光滑系统数值仿真中[17-19]，这里不再赘述.

2 Duffing振动系统应用实例

考虑如下的经典非线性Duffing振动系统

(7)

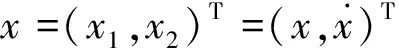
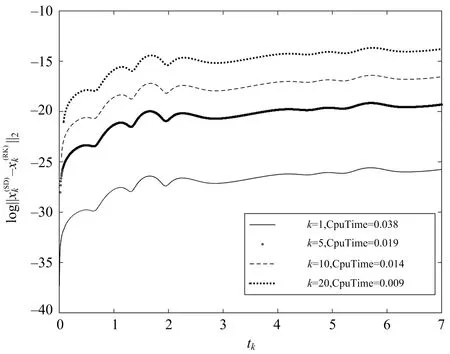
图1 轨道摄动法与RK直接法之间的误差

从图1可以看到，当k值越大，两种数值解的误差逐渐变大，但在有限的积分时间内，基本满足一定的精度要求. 同时，随着k值的增大，消耗的计算时间在逐渐减少，计算效率在不断提高. 所得数值仿真的结果与上一部分的分析结果是一致的.

为了进一步验证上述方法在解决多初值问题方面的有效性和高效性，取以(0,1)为中心长度为0.1的正方形单元格A，在该单元格内随机均匀选取10 000个初始点. 对于每个初始点，分别用4阶RK直接积分法和轨道摄动法求解系统(7)，积分长度取为T=2π/ω,积分步数取为N=1 000.在实施轨道摄动法时，其参考轨道的初始点取为单元格的中心(0,1).

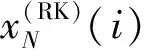
(8)

此外，完成上述数值仿真RK直接法和轨道摄动法所使用的CPU时间分别为26.79 s和1.24 s. 可见，对于大规模的胞映射算法的实现，轨道摄动法不仅具有较高的精度，且大大提高了计算速度.

图2 多初值情形下RK直接法和轨道摄动法的比较图

固定系统(1)的部分参数为a=1,b=0.15,c=1,ω=1，考虑外谐和激励的强度对系统(7)全局动力学的影响，选取Poincare截面为

(9)

将上述轨道摄动积分算法运用到广义图胞映射方法中，深入分析分叉和激变前后系统(7)的全局动力学行为. 在广义图胞映射算法中，感兴趣的状态空间选取为D={(x1,x2):-2≤x1≤2,-2≤x2≤2}，将感兴趣的区域D均匀划分为200×200个胞，利用边界内部组合方法在每个胞内取100个采样点. 图3中，符号B(i1,i2,…,ik)表示第i1至第ik个吸引子的吸引盆边界，S(i1,i2,…,ik)表示吸引盆边界B(i1,i2,…,ik)上的鞍. 胞映射方法中采用RK直接法和轨道摄动法所得结果几乎一致，这里略去RK直接法所得的全局结构图.

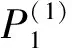
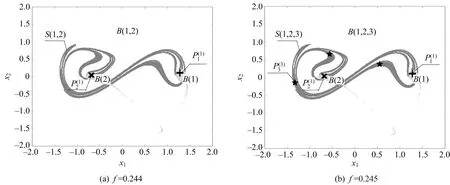
图3 全局结构图

3 结束语

多初值问题的数值积分是胞映射算法效率的瓶颈. 论文针对胞与胞之间的建立机制，借助摄动法的思想，发展了轨道摄动积分法，大大提高了胞映射算法的计算效率.

以典型的Duffing振动系统为计算实例，讨论了轨道摄动积分法的有效性和计算效率. 同时，分析了系统的全局动力学. 研究表明：在一定的参数条件下，系统存在多吸引子共存现象，捕捉到了共存的稳定周期吸引子和非吸引的混沌鞍；随着外谐和力的变化，周期吸引子与边界混沌鞍发生碰撞，导致该吸引子及其吸引盆一同消失.