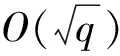一种组合Pohlig-Hellman和Pollard ρ的迭代求解离散对数方法
2019-05-08胡建军李恒杰
胡建军,王 伟,李恒杰
(兰州文理学院 数字媒体学院, 甘肃 兰州 730010)
尽管如此,学者很少关注Pollardρ和Pohlig-Hellman两个算法的有效融合.针对这一问题,结合Pohlig-Hellman和Pollardρ两个算法各自的长处,利用文献[2]的迭代函数,作者提出一种基于Pohlig-Hellman的Pollardρ混合迭代求解离散对数的方法.方法的思想是:当阶的素因子小于等于光滑界时,使用Pohlig-Hellman算法迭代求解;当阶的素因子大于光滑界时,使用Pollardρ算法迭代求解.同时,分析了混合算法的效率.最后通过实例验证了结论的正确性和有效性.
1 相关知识
1.1 Pohlig-Hellman算法概述
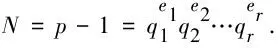
由Fermat定理,有
gN≡1modp,
所以,有
从0到qi-1尝试使等式成立的z0的值,并保存z0.另外,由于
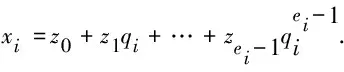
1.2 Pollard ρ算法概述
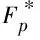
(1)
且ai和bi的序列分别如式(2)和(3)所示, 初始a0=b0=0.从而, 序列中的每个元素具有ri=yaigbi的形式,序列ri=yaigbi可看成是一个随机游走.
(2)
(3)
执行一个6元组(ri,ai,bi,r2i,a2i,b2i)的序列, 直到找到ri=r2i,即yaigbi=ya2igb2i.
令
m≡ai-a2i(modN),
n≡b2i-bi(modN),
则
利用扩展的欧几里得算法寻找一个满足d=gcd(m,N)=λm+μN的λ和μ.从而λm≡d(modN),因此yd=gλn, 且λn一定在形式kd中(由于左边是第d个幂).利用第d个根, 得到
其中:k=((λn(modN))/m)(modN).
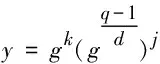
loggy=(k+(N/d)*j)(modN).
1.3 迭代函数
假设t0,t1,t2,…是一个大于1的素数序列,则考虑如下序列
(4)
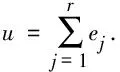
对于任意的整数x,0≤x≤N-1,有式(5)成立
x=z0+z1t0+z2t0t1+z3t0t1t2+…+zu-1t0t1…tu-2,
(5)
其中:系数zj满足0≤zj 假设 sk=z0+z1t0+z2t0t1+z3t0t1t2+…+zk-1t0t1…tk-2,0≤k 则k+1个同余系数乘积之和的迭代公式为 sk+1=sk+zkt0t1…tk-1. 由式(4),(5)可得 (6) 从式(6)可以看出,z0由x≡z0(modt0)计算,z1由x-z0≡z1t0(modt1)计算,如此重复,最后zu-1由 x-su-2≡zu-1t0t1…tu-2(modtu-1) 计算,u≥2,即 x≡su-2+zu-1t0t1…tu-1modtu-1, 因此式(6)就是求解的迭代函数. 引理2给出了离散对数求解的概率上界,引理3给出了离散对数求解的下界. 定义令b是一个正整数,若阶N的所有素因子都小于等于b,则称b是N光滑的. 算法1 Pohlig-Hellman iteration algorithm Input:p,g,y,b Output:sb 1 sb=0,δ=1,η=1,ζ=1,N=p-1 //δ用于计算幂模,η用于迭代计算. 2 γ=inverse(g,p) 3 for i=1 to b 4 {δ=δ*Arr(i),η=η*ζ //δ存储前i个光滑因子的积,η存储前i-1个光滑因子的积. 5 if Arr(i)<>ζ then gh=gN/Arr(i)(modp) 6 yt=γsb(modp) 7 yh=y*ytN/δ(modp) 8 for j=0 to Arr(i)-1{ if ghj(modp)=yh then {sb=sb+j*η(mod N),exit}} 9 ζ=Arr(i) 10 } 11 return sb 12 end 在算法2中,先将y值转换为新值y′,即y′=inverse(g,p)sby(modp),然后再计算y′的离散对数值,x=loggy′(modN)为所要求解的离散对数.算法2直接引用了引理1,2的结论.下面是算法2的设计实现. 算法2 Pollardρiteration algorithm Input:p,g,y,b,sb,pl Output:sp 1 sp=sb,a1=b1=0,r=1,δ=1,η=1,ζ=1,N=p-1 2 γ=inverse(g,p),y′=γsb*y(modp) 3 for θ=b+1 to pl 4 {δ=δ*Arr(θ),η=η*ξ 5 if Arr(θ)<>ξ then gh=gN/Arr(θ)(modp) 6 yt=γsp(modp),yh=y′*ytN/δ(modp) 8 Do while i<=tl // tl为游走到环上需要的步数,该循环将游走到环上. 9 { if r<=p/3 then {r=r*yh,a1=a1+1} 10 else if p/3 11 else {r=r*gh,b1=b1+1} 12 i=i+1 13 } 14 rs=r,a2=a1,b2=b1,cnt=0 15 Do //在环上查找碰撞. 16 { if r<=p/3 then {r=r*yh,a2=a2+1} 17 else if p/3 18 else {r=r*gh,b2=b2+1} 19 cnt=cnt+1 21 if rs=r and a1<>a2then 22 {m=(a1-a2)(mod N),n=(b2-b1)(mod N),d=λm+μN(mod N) 23 k=(λ*n/d)(mod N),β=gk(modp),j=0,ε=1 24 yhh=ε*β(mod p) 25 Do while y’<>yhh and j 26 {ε=y’*yhh(mod p),j=j+1,yhh=ε*β(mod p)} 27 if y’=yhh then return sp=sp+k+j*N/d(mod N) else return failure 28 } 29 else return failure 30 ζ=Arr(θ) 31 } 32 end 定理1设Arr(pl)是阶N的最大素因子,且大于光滑界b的素因子个数仅为1,则混合算法经过下列步数找到一次碰撞: 证明因为y和g在算法2中均需要执行N/Arr(pl)的幂次求余运算,这就保证了Arr(pl)是循环子群的阶,而是Arr(pl)又是素数,由引理2可知,结论成立. 定理2设大于光滑界b的素因子个数为τ,算法2迭代一次的成率为v,则混合算法的成功率为ντ. 证明因为迭代算法是在前一计算结果正确的基础上重复执行,而前一迭代和后一迭代又是互相独立的,所以,混合算法的成功率为ντ. 由定理2可知,要确保求解获得更大的概率,迭代次数要尽可能地小,最好不超过2(因为当超过2时,成功求解的概率将大于等于25%),这样混合算法才具有求解的优越性. 假设p=71,生成元g=7,光滑界为5,y=32,计算x=log732的离散对数30. 因为N=p-1=70=2*5*7,所以Arr(1)=2,Arr(2)=5,Arr(3)=7,从而得b=2,pl=3. 首先,来看算法1的执行过程.初始sb=0,δ=1,η=1,ζ=1,N=p-1=70.计算γ=inverse(g,p)=61.执行for循环体,当i=1时,δ=1*Arr(1)=2,η=η*ζ=1.因为Arr(1)<>ζ,所以gh=770/2(mod71)=70,yt=610(mod71)=1,yh=(32*1)70/2(mod71)=1.又700=1,从而sb=sb+j*η=0,ζ=Arr(1).当i=2时,δ=δ*Arr(2)=10,η=η*ζ=2,因为Arr(2)<>ζ,所以gh=770/5(mod71)=54,yt=610(mod71)=1,yh=(32*1)70/10(mod71)=1.又540(mod71)=1,从而sb=sb+j*η=0,ζ=Arr(2).即算法1的迭代结果为0.1.4 Pollard ρ算法理论分析基础
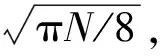

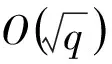
2 混合迭代算法设计
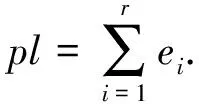
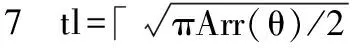
3 混合迭代算法分析
3.1 算法分析
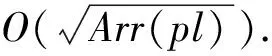
3.2 算法实例

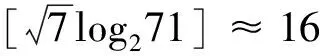
4 结束语