基于两种螺旋桨建模方法的全附体船模斜拖试验数值模拟
2019-05-08邹早建郭海鹏
刘 义, 邹早建, 郭海鹏
(1. 中国船舶及海洋工程设计研究院, 上海 200011;2. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240;3. 上海交通大学 海洋工程国家重点实验室, 上海 200240)
船舶操纵性是与船舶航行安全性密切相关的非常重要的船舶航行性能,准确预报船舶操纵性对保证船舶航行安全具有重要意义.在船舶设计阶段,准确预报船舶操纵性是至关重要的.十多年来,计算流体动力学(CFD)方法在船舶水动力学学科得到日益广泛的开发和应用,其发展异常迅猛.在船舶操纵性方面,CFD方法也已得到成功的应用,包括数值模拟约束模试验以获取操纵运动数学模型中的水动力,以及对操纵运动进行直接数值模拟以实现对操纵性的直接预报.这方面的研究已成为了国际上的热点和前沿课题[1].
数学模型加计算机模拟的方法是一种在船舶设计阶段预报操纵性的最常用的方法,而基于CFD方法对约束模试验进行数值模拟是现阶段获取船舶操纵运动数学模型中的水动力导数的一种有效方法.Yao等[2]基于OpenFOAM开发RANS求解器,对大型油轮KVLCC2船模的斜拖试验、旋臂试验和PMM(平面运动机构)纯横荡试验进行了数值模拟.王建华等[3]基于非定常RANS方程和重叠网格技术,对军船DTMB5415裸船体模型的PMM纯首摇试验进行了数值模拟.冯松波等[4]应用CFD软件Fluent对KVLCC2船-舵系统模型的斜拖试验进行了数值模拟.当采用CFD方法数值模拟全附体约束模试验时,重点和难点之一在于螺旋桨的建模.目前应用CFD方法对真实几何形状的螺旋桨(实桨)和船体相互干扰进行全附体船舶操纵运动数值模拟已经开展了一些研究.Badoe等[5]采用实桨建模方法,分析了斜流下的船-桨-舵干扰问题;类似地,Wang等[6]数值模拟船舶的斜拖试验,分析了螺旋桨在斜流中的负荷.除实桨建模外,另一种方法是以力场模拟代替真实螺旋桨,即体积力法.国内外已有众多学者应用体积力法研究过船-桨-舵干扰和操纵性等问题[7-9].但在约束模试验数值模拟中,基于实桨建模和基于体积力建模之间的差别却少有涉及.
本文应用STAR CCM+软件,采用雷诺平均Navier-Stokes(RANS)方程求解方法并选取Realizablek-ε湍流模型封闭黏性流体流动控制方程,对全附体的集装箱船KCS船模斜拖试验的黏性流场进行了数值模拟,其中对螺旋桨建模分别采用了体积力模型和实体螺旋桨模型.通过将数值计算结果与基准试验数据进行对比,验证了数值方法的正确性;同时,对比分析了两种螺旋桨建模方法在计算效率和计算精度方面的差异.
1 数学模型
1.1 坐标系
如图1所示,建立两个右手坐标系:空间固定坐标系O0-x0y0z0和随船运动坐标系O-xyz.空间固定坐标系原点位于静水面内船舯运动初始位置.O0-x0y0平面与静水面重合,O0z0轴垂直向下.随船运动坐标系原点选择在船舯处,随船体一起运动,Ox轴从船尾指向船首,Oy轴指向右舷.作用在船体上的水动力在x轴和y轴的分量分别为X和Y;绕船体z轴的转首力矩为N.船体的平动速度U在随船运动坐标系中的纵向和横向分量为u和v,其中:u=Ucosβ,v=-Usinβ,U=|U|,β是漂角.舵的法向力记为FN.
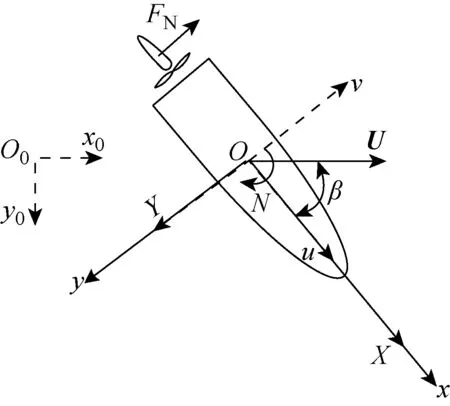
图1 坐标系Fig.1 Coordinate systems
1.2 流体流动控制方程
船舶周围三维黏性流场可由雷诺平均的连续性方程和动量方程(RANS方程)来描述:
(1)
(2)
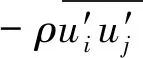
1.3 螺旋桨体积力模型
本文采用Hough等提出的体积力模型[11],将体积力以源项的形式加入控制方程,即式(2)中.该方法通过对螺旋桨所在区域施加推力和转矩代替桨叶表面载荷,计算公式如下:
(3)
(4)
式中:fbx和fbθ分别为轴向力和切向力在螺旋桨计算域内的分布;rc为螺旋桨区域内任意一点至螺旋桨轴线的距离;RH为桨毂半径;RP为螺旋桨半径;TP为螺旋桨推力;QP为螺旋桨转矩;ΔP是螺旋桨盘面厚度,一般取值为桨直径的2%.在实际计算中,施加体积力的过程为将推力和转矩施加给螺旋桨作用区域,进而对控制方程进行求解计算.
2 数值求解
2.1 研究对象
选取KCS船模为研究对象,该船型是国际专题研讨会SIMMAN2014[12]所采用的标准船型之一,船后舵和桨的几何数据也由SIMMAN2014提供.数值研究采用的缩尺比和主尺度如表1所示.选取日本海上技术安全研究所(NMRI)提供的模型试验数据(缩尺比1∶75.50)[13]进行比较,以验证本文的数值方法.

表1 KCS船主尺度Tab.1 Main particulars of KCS
2.2 计算域及边界条件
计算域和边界条件设置如图2所示,计算域总长度为5Lpp,宽度为2.5Lpp,水深为2.5Lpp,自由面以上高度为1.2Lpp.边界条件:船体和舵表面设置为固壁边界条件;除了出口设置为压力出口外,其他计算域外面的5个面均设置为速度入口.在两个侧面、入口和出口处,设置人工数值阻尼来降低数值振荡.
2.3 网格划分
本文应用CFD软件STAR CCM+[14],选取切边网格生成器(Trimmed Mesher),通过切割几何表面,自动生成以六面体为主的网格.通过棱柱层生成器(Prism Layer Mesher)在壁面边界上产生正交棱柱网格,从而精确求解流场.采用网格质量修正数值模型(Cell Quality Remediation)来提高求解精度.采用混合壁面函数来处理壁面边界条件.设置计算域网格初始目标尺寸(Target Size)为Lpp/30,在自由面、船首、船尾、舵以及桨周围进行网格加密.棱柱层网格有6层,总棱柱层厚度为Lpp/150,拉伸比为1.5,无量纲化的壁面到第一层网格的距离y+≈25.由于采用混合壁面函数,生成的壁面边界层厚是可接受的.在应用体积力法(记为BF法)进行螺旋桨建模时,对激励盘位置处的网格进行适当加密.在采用实桨法(记为RP法)进行螺旋桨建模时,对实桨进行网格离散,实现螺旋桨旋转采用的方法是在桨附近产生一个圆柱形的运动域,定义这个运动域的旋转速度,在其表面设置滑移壁面边界条件,运动域与外部区域之间使用交界面边界条件,使得螺旋桨域和整体域耦合,这种方法称作滑移网格法.图3给出了船体附近的网格结构.基于BF法和RP法得到整个计算域的网格总数分别为1.5×106和1.8×106.
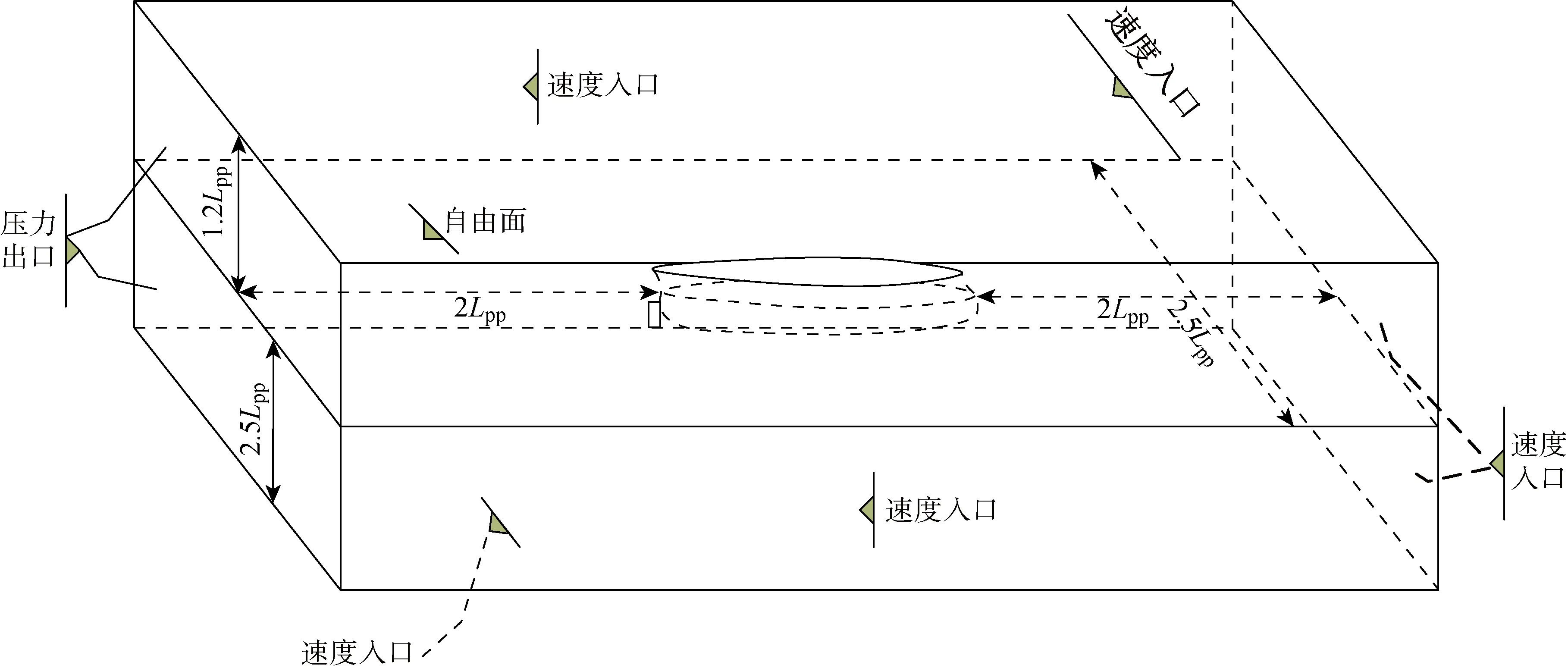
图2 计算域和边界条件Fig.2 Computational domain and the boundary conditions

图3 船体附近网格Fig.3 Grid structure around the ship
2.4 数值方法
本文应用STAR CCM+进行流场数值模拟,基于有限体积法离散方程,其中瞬变项采用一阶全隐式方案进行离散,对流项采用二阶迎风格式,耗散项离散后存在一个二次梯度(交叉扩散)项,采用二阶的高斯-最小二乘混合法求解梯度.采用分离流模型结合SIMPLE算法和Rhie-Chow修正方法分别求解压力和速度项.通过VOF(Volume of Fluid)方法构造自由面.船体的运动由动态流固耦合运动模块(DFBI)计算获得.在基于RP法的非定常计算过程中,为保证求解精度,时间步长小于1/(50nP),其中nP是螺旋桨转速,而BF法的螺旋桨用体积力代替,可以适当放大时间步长.所有计算都基于两台戴尔高性能计算服务器(36核/72线程,2.32 GHz).
3 数值结果分析
3.1 水动力结果


图4 全附体KCS船模斜拖试验水动力结果比较Fig.4 Comparison of hydrodynamic forces in oblique-towing tests for the fully appended KCS model

β/(°)BF法线程求解器总计算时间/sRP法线程求解器总计算时间/s065.06×104301.00×1052108.67×104142.49×105488.69×104201.48×105688.68×104162.28×105861.84×105201.57×1051261.84×105301.85×1051661.84×105301.76×10520367.68×104501.07×105平均10.751.18×10526.251.69×105

图5 螺旋桨尾流轴向速度比较 (x/Lpp=0.488 3)Fig.5 Comparison of axial velocity contours in propeller slipstream (x/Lpp=0.488 3)
3.2 流场结果
进一步地,从流场细节进行比较分析.由于舵在螺旋桨后面,所以准确预报桨下游处流场是很重要的.图5分别给出了基于BF法和RP法获得的β=0°和6°时桨盘面后方(x/Lpp=0.488 3)流体的轴向速度u′(u′=u/U)分布;为讨论方便,图5(a)中定义了4个象限(I到 IV).当β=0°时,对于RP法来说,由于是右旋桨,桨叶从 III、IV 象限运动到I、II 象限.另一方面,船体的运动使得尾流场存在一对内旋反向对称的舭涡, 导致横向速度方向和桨 III、IV 象限的横向速度方向相同,和I、II 象限相反,致使桨叶剖面在 III 和 IV 象限的攻角减小,相对应地在I、II 象限攻角增大,从而使得 III、IV 象限的轴向速度小于I、II 象限的轴向速度(图5(b)).而对于BF法,反而是I、II 象限的轴向速度稍小于 III、IV 象限的轴向速度(图5(a)).当β=6°时,尾流场与直航工况不同,在船体背风面,产生明显的钩状尾流.在桨盘面内,轴向速度最大值并没有因为漂角的影响改变,只是其分布由于入流速度分布的改变而稍有改变(图5(c)、(d)).

图6 船尾表面压力和中纵剖面轴向速度比较Fig.6 Comparison of pressure on the stern region and axial velocity contours on the central longitudinal section
图6给出了β=0° 和6° 时船尾附近中纵剖面轴向速度和船、桨、舵表面的压力系数Cp(Cp=p/(0.5ρU2))分布.从图中可以看出,β=0° 时,在舵的前缘存在驻点,但是越往下游,由于舵的厚度减小,压力逐渐减小,在舵后缘压力又升高.在舵的左舷前缘上半部分可以看到高压区,对应的右舷同样位置是一个低压区.在前缘的下半部分存在相反的压力分布.β=6°时,由于左舷是迎风面,舵左舷的高压区增大,低压下降.相应地,舵右舷的高压区减小,低压区增大.不论是直航还是斜航,RP法的诱导速度稍微大于BF法的诱导速度,导致RP法得到的舵的低压区增大,也就是说RP法得到的舵法向力偏大,从图4(e)中也能看到.总体而言,两种方法的压力和轴向速度分布是类似的.
虽然试验方法具备较高的可靠性,但由于试验费用高、周期长而受到限制,目前船-桨-舵系统斜拖试验中的尾流轴向速度等流场细节是很难获得的.由于缺乏流场细节测量数据,所以本文无法进行流场信息的验证.
4 结论
本文分别采用体积力法和基于实桨的滑移网格法对螺旋桨进行建模,数值模拟了全附体KCS船模斜拖试验的黏性流场.通过和国际发布的基准试验数据对比,验证了本文提出的数值方法的可靠性.此外,对比基于体积力法和滑移网格法的计算结果发现,体积力法虽然无法捕捉由于桨叶旋转导致的流场细节变化,但对船-桨-舵整体的水动力和力矩的预报均比较准确.而采用基于实桨的滑移网格法,需要的计算时间要比前者长得多,因而计算成本很大.故对于船舶操纵运动水动力计算及操纵性预报问题,如果不需要详细的螺旋桨流场信息,可采用体积力法进行螺旋桨建模.
数值模拟KCS船模斜拖试验的计算结果表明,桨推力、船体的纵向力和横向力、转首力矩以及舵的法向力对应的平均力同试验结果的误差是可接受的;但对于应用体积力法进行螺旋桨建模得到的桨推力和船体纵向力的数值计算精度以及相应的数值不确定度需要进一步开展研究.
