基于动-静叶片相位调制的冷却风扇离散噪声控制
2019-05-08彭志刚欧阳华吴亚东
彭志刚, 欧阳华, 吴亚东, 田 杰
(1. 上海交通大学 机械与动力工程学院,上海 200240;2. 上海博泽电机有限公司,上海 201801)
符号说明
b—点声源到声源阵列中心轴线的半径
c—声速
dk—风扇叶片脉动压力第k阶次的幅值
D2—叶轮叶顶直径
Hn—第n次谐波,Hn=nZ(n=1,2,3,…)
ko—波数
ps—静压
q—静叶编号,q=0, 1, …,v-1
qV—风扇送风的体积流量
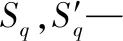
u2—叶顶圆周速度
W—声功率
Z—风扇叶片数量
αq—第q阶声源与观察者连线的夹角
ΔF—来流经过静叶产生脉动力的幅值
μi—相邻叶片的夹角(i=1,2,…,Z)
ρ—空气密度
φ—风扇叶片周向角度
φj—均布叶片风扇第j个叶片的周向角度(j=1,2,…,Z)
χ—静叶角度分布参数,χ∈(0,1)
ψ—声源轴线与声源阵列平面法线的夹角
ω—角速度
气动噪声是汽车冷却风扇的主要噪声源,包括宽频噪声(本底噪声)和离散噪声(叶片通过频率噪声及其谐波成分和其他突出的阶次噪声).宽频噪声主要影响车辆外部的通过噪声总值;离散噪声不仅加剧了运行车辆对周遭环境的噪声污染,而且降低了车内驾驶员及乘客的舒适感.衰减离散噪声方法的研究始于20世纪中期.Lowson[1]的研究结果表明,叶片相位调制是衰减离散噪声最有效的方法之一,且其对气动性能的影响较小.
文献[1]总结了降低压气机叶片脉动力辐射噪声的潜在方法,并指出交错叶片和相对动叶倾斜的静叶设计可应用于轴流式水轮机设计.文献[2-4] 分别介绍了单转子的叶片间距设计和离散噪声的预测方法.文献[5-12]探讨了风扇叶片的表面流场特性[5-9]和周向分布方式等因素[10-11]对离散噪声、气动性能和心理声学参数[12]的影响.
然而,上述研究方法仅适用于通过改变转子风扇的参数特性来改善旋转机械噪声频谱中离散噪声的情况.众所周知,离散噪声也会受到静叶,尤其是下游静叶的影响[13-15].Duncan等[16-17]提出一个基于声学百叶窗效应的理论模型.该模型通过控制静叶角度分布参数(χ)来预测风扇下游静叶受到的脉动力对上游风扇声辐射某些特定阶次的衰减效应,通过合理设计χ可以有效地控制中速风扇的某些特定阶次噪声.
现有的这些研究虽然涉及如何改善离散噪声,但是忽略了在旋转机械的早期设计阶段就纳入离散噪声设计的重要性.本文在充分考虑动叶片声辐射和静叶片阶次衰减效应的基础上,提出一种在旋转机械设计初期能够同时兼顾转子和定子离散噪声性能的快速预测方法,极大地缩短了设计周期,并且节约了人力成本.
1 相位调制
冷却风扇组件(CFM)在运转时会对周围工作环境产生声辐射,其离散成分的主要影响因素有叶片表面脉动力、动静干涉和非对称气流等.当风扇叶片在周向呈均匀分布时,Hn是CFM噪声的主要离散成分;当风扇叶片在周向呈非均匀分布时,由于其脉动力的相位产生变化,谐波噪声的声能量向其他阶次扩散,使得自身声能量有所降低,这种现象即为风扇离散噪声控制中的相位调制.
上游来流经过CFM静叶产生的声辐射主要为偶极子声源,其在周向阵列中受到来流旋转脉动力(主要来自于上游的风扇叶片)的影响.同样地,通过调节静叶的周向分布角度,可以控制脉动力对静叶阵列激励的相位差,从而改变其噪声在特定阶次上的分布能量.前者是主动激发噪声;后者则通过调制脉动力来抑制某些特定阶次的噪声.下面详细介绍这些原理和方法中的关键参数.
1.1 转子风扇分布参数
(1) 周向非均布叶片保证质心对中;
(2) 相邻叶片夹角μi大于叶片的周向角;
(3) 推荐相邻叶片的夹角变化不超过20%,且随之产生的气动性能波动小于7%[18].
条件(1)亦称为质心条件,能够保证风扇质心分布在旋转轴上,从而使得运转过程中不会产生较大的振动,应当满足
(1)
Ewald等[3]提供了非均布叶片布置的经典方法,其叶片周向角度满足
(2)
式中:A为非均布系数,当A=0时,为均布排列方法;n为大于1的正整数,当n=2时,可避免风扇噪声频谱中相邻阶次的噪声同时出现较高峰值.将式(2)应用于质心条件,得出的误差小于 0.05°.该误差在合理范围内,将被后期风扇制造过程中产生的偏差所覆盖.
风机的离散噪声幅值主要取决于叶片顶部的压力波动[19].风扇的脉动压力可由Dirac函数δ表示:
(3)
根据Fourier变换,式(3)可处理为
(4)
第k阶次压力脉动幅值定义为
(5)
则第k阶离散噪声的相对水平为
ek=20 lgdk+C
(6)
式中:C为常数.Akaike等[20]进一步在轴流风机的应用中确认了以上计算方法的正确性.通过调整参数A,离散噪声的水平可通过式(2)~(6)进行快速预测.当Z=7,A=0.175 时,根据上述公式推导的各阶次相对噪声水平如图1所示,此处取C=40.
对于7叶片风扇,声能量主要集中于叶片通过噪声一次谐波(H1,即图1中的7阶次)及其谐波成分二次谐波和三次谐波(H2和H3,即图1中的14阶次和21阶次).H1,H2和H3的噪声水平随参数A的变化趋势如图2所示.H2和H3的噪声水平可以根据离散噪声优化的需要进行调控.当A=0.17 时,H2的噪声水平显著降低;当A=0.11 时,H3的噪声水平显著降低.然而,随着A值的增加,H1的噪声水平变化平缓,说明该方法难以控制H1的噪声水平.对于如图3所示的非均布叶片风扇,当A取值过大时,相邻叶片将会出现重叠的现象,见图3(b),这时不满足条件(2),这对后续风扇模具开发流程而言是不可接受的.
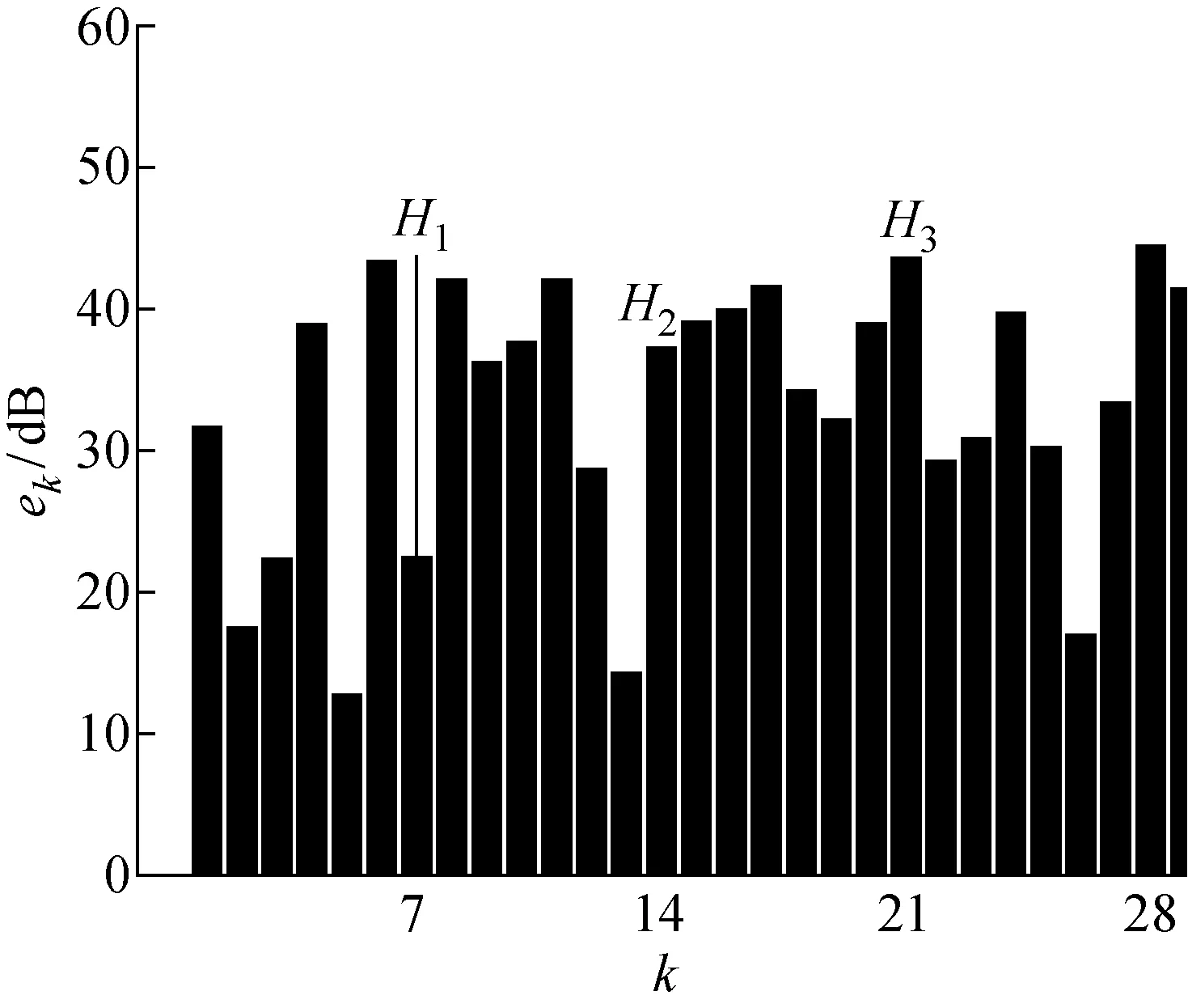
图1 离散噪声水平分布Fig.1 Discrete noise level
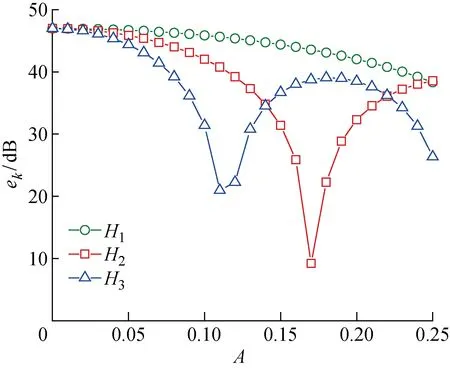
图2 谐波噪声水平趋势图Fig.2 Harmonic noise level
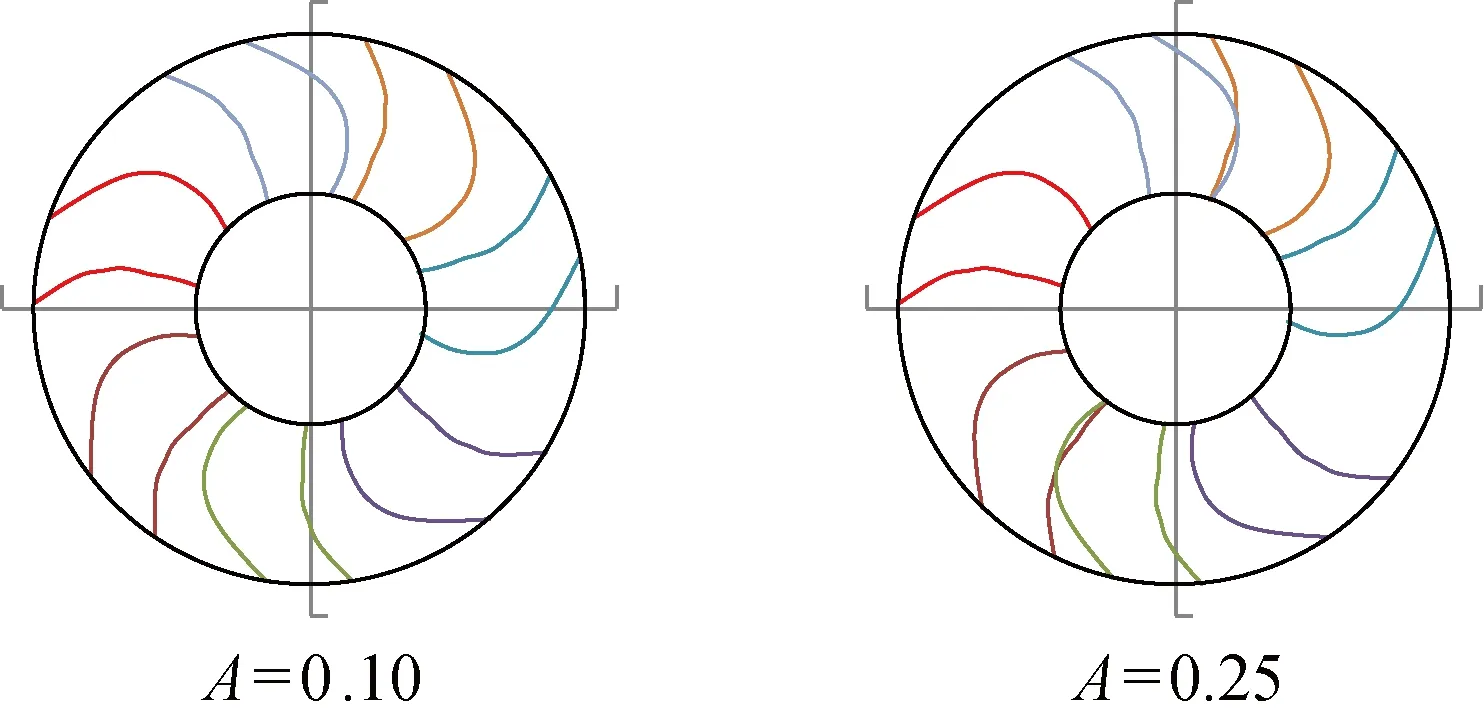
图3 非均布叶片风扇Fig.3 Fan of uneven spacing blades
1.2 静叶角度分布参数
静叶在离散噪声的调制中有着重要作用,将其与转子风扇叶片通过非均布技术结合在一起,可对风扇总成离散噪声进行系统性优化.根据文献[21],本文设定子与转子的轴向间距为20 mm.
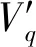
(7)
本文不考虑叶片脉动力产生的尾迹在径向的差异.图4所示为辐射点声源的简化阵列模型,P点的压力波动和所有静叶的辐射声功率可表示为[17]
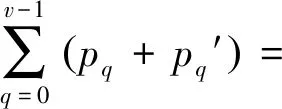
kobsinθcos(φ-βq)-nβq]+
(8)

(9)
若叶片脉动力与频率无关,则ko与S为常数,式(9)可以转化为
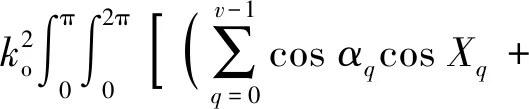
sinθdφdθ
(10)
式中:

cosαq=cosθcosψ+
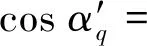

图5 静叶阵列的百叶窗效应图Fig.5 “Venetian blind” diagram of vane array
式(10)从数学角度具体描述了在静叶声学百叶窗效应的影响下,点声源阵列辐射的声功率分布.在不同χ下,对应v=3(即6静叶)和v=4(即8静叶)两种情况,基于MATLAB软件求解式(10).声功率相对水平与阶次的函数曲线如图5所示.由图可知,对于7叶片风扇,当下游匹配6静叶,χ=0.2时,可以有效地抑制H1的噪声水平;当下游匹配8静叶,χ=0.3时,可以有效地抑制H1的噪声水平.
综上所述,在风扇总成设计初期,合理地设计转子调节参数A和定子调节参数χ,系统将可能获得更好的离散噪声性能.首先,考虑不平衡因素的影响,调整转子叶片参数A进行阶次噪声的初步布置;其次,根据声学百叶窗效应理论,设计不同数量的静叶参数χ,并将其锁定在特定的目标阶次上进行优化,以弥补第一步阶次噪声设计中叶片宽度限制对噪声性能产生的影响;最后,根据静叶结构强度的设计要求,确定静叶个数,完成总成设计.
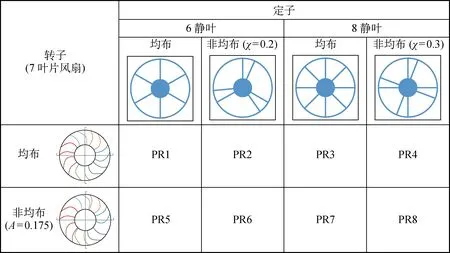
图6 风扇与静叶组合方案矩阵图Fig.6 Matrix of fan and stator unit proposals
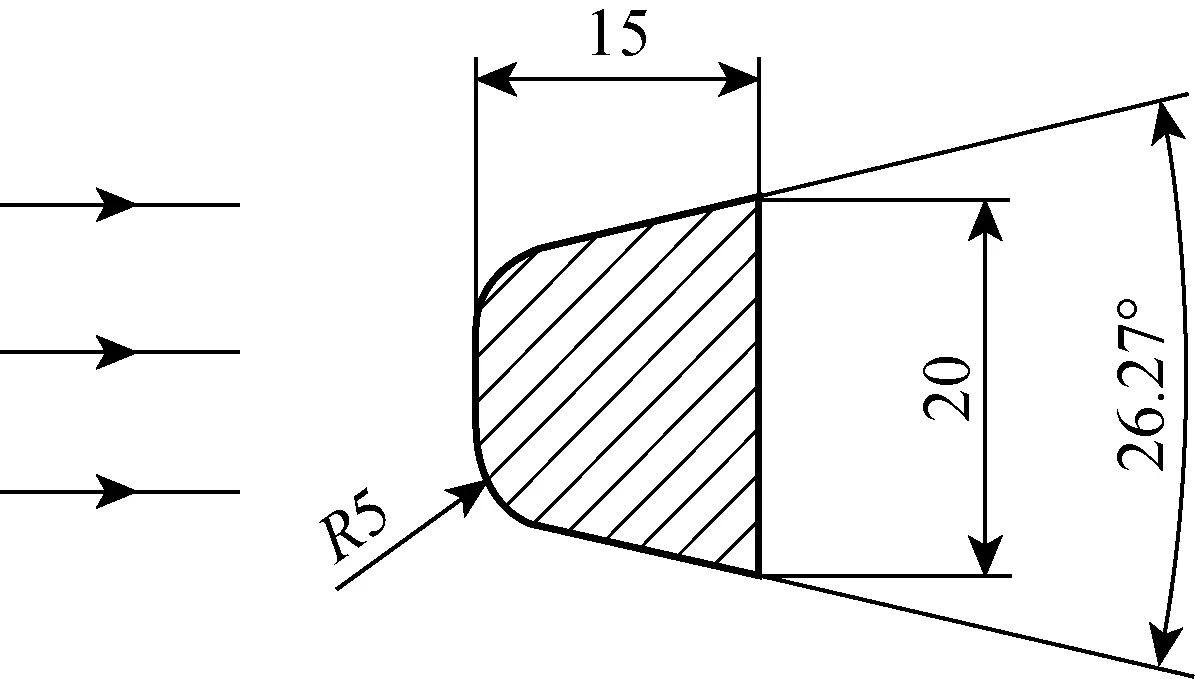
图7 静叶截面尺寸 (mm)Fig.7 Section of vane (mm)
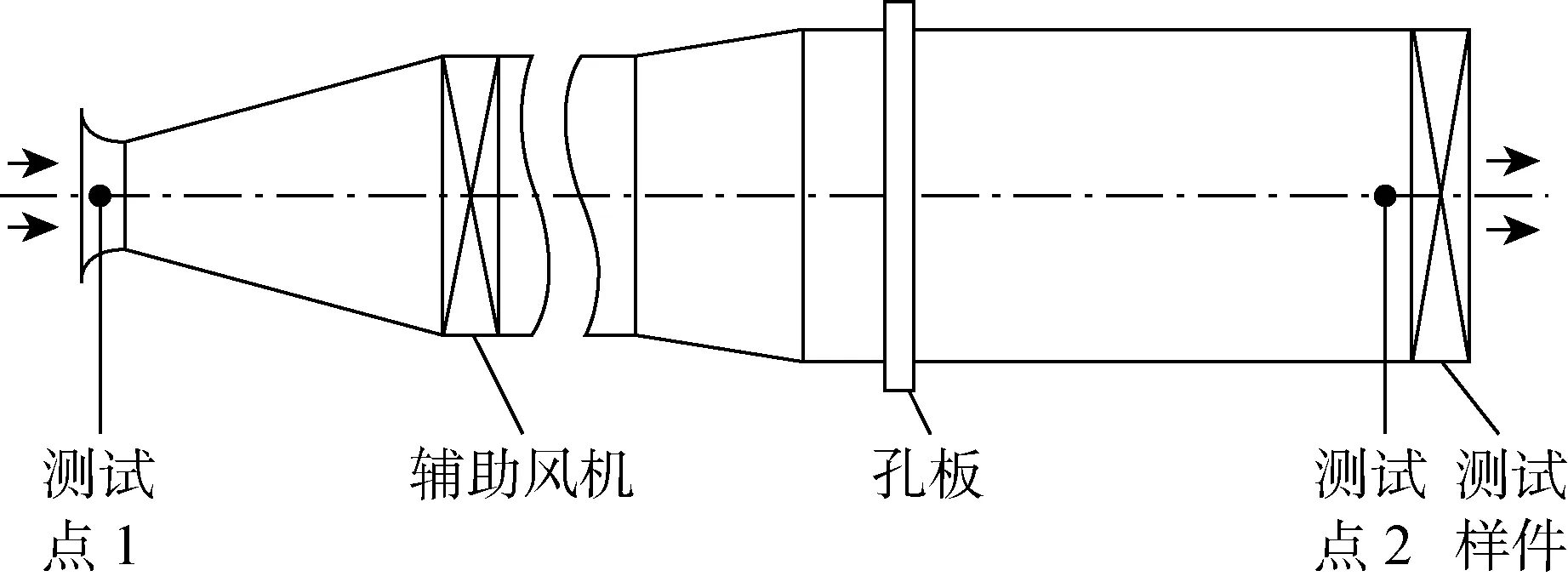
图8 气动性能测试台示意图Fig.8 Test bench for air performance
2 实验验证
为了验证A-χ动-静叶片相位调制组合方法的有效性及正确性,将该方法用于设计汽车冷却风扇组件.本文不考虑风扇的机匣及风扇组件上游散热器和冷凝器对来流的影响,以避免来流不均匀和风扇叶顶与机匣间的脉动涡流引起的对实验结果的影响.
图6列出了8个转子风扇和定子静叶组合方案的矩阵.2个转子风扇叶片与4个定子静叶的设计完全相同,不同的是各自的叶片夹角.为了避免几何差异和结构强度差异对局部流场的影响,所有方案中的风扇和定子均为铝合金材料.定子静叶的截面形状如图7所示,该形状为汽车冷却风扇静叶的常规设计形状,可以保证电动机安装位置的结构强度和系统运转的稳定性.
在噪声测试之前,首先通过实验的方法研究非均布叶片对风扇气动性能的影响,气动性能测试台示意图如图8所示.该风洞设计参考《工业通风机用标准化风道进行性能试验》(GB/T 1236-2000),其内径为 0.72 m,测试点1和测试点2分别用于测试空气流量和静压升.风扇转速为 2 900 r/min,通过更换不同密度的孔板和调节辅助风扇的转速,一共测试了6个工作点以获得风扇的气动性能曲线.
定义流量系数ζ和静压系数γs分别为
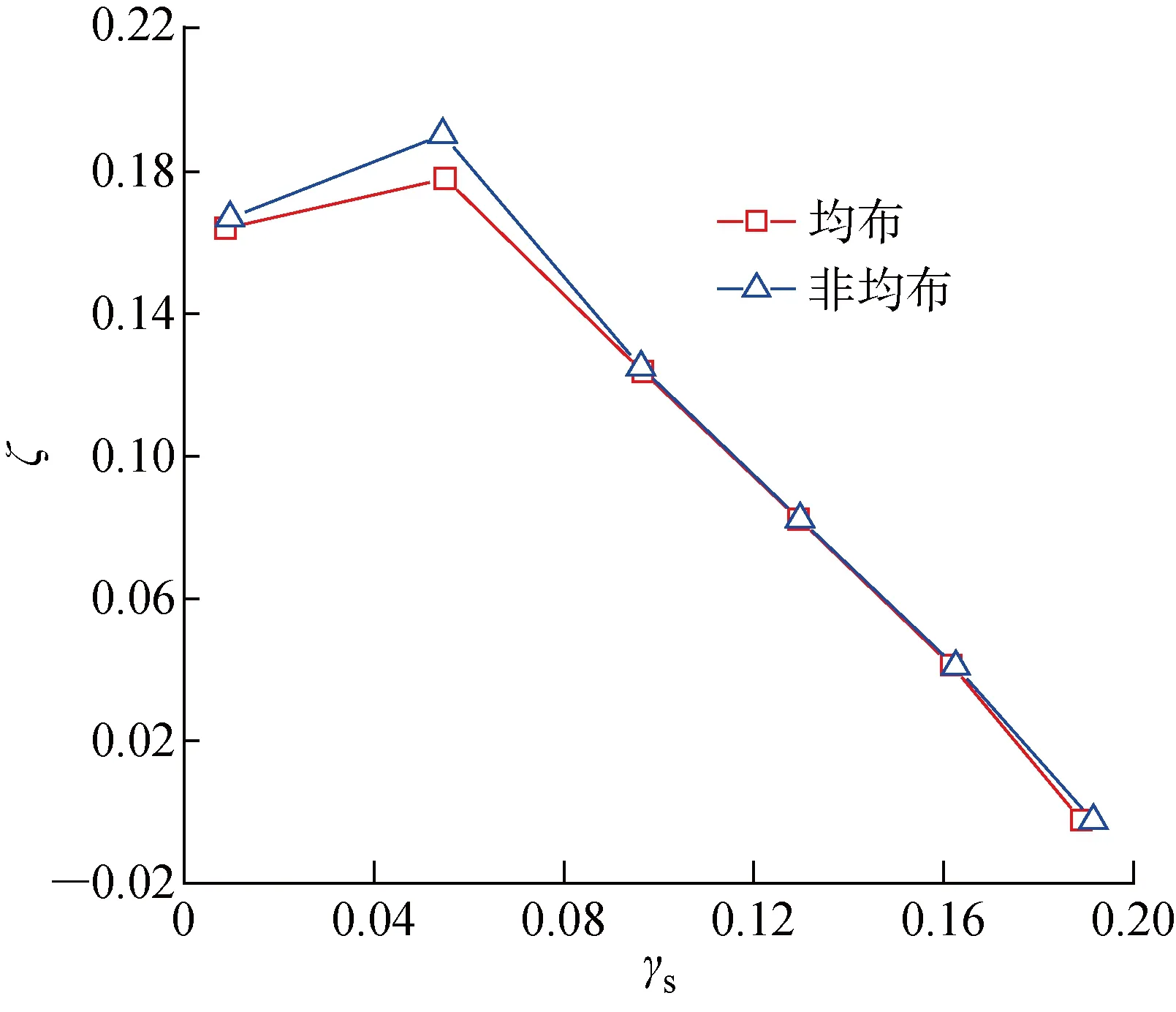
图9 气动测试结果Fig.9 Aero flow test results
实验结果如图9所示,两种风扇的气动性能非常相近,在ζ接近 0.055 的高压区,气动性能的幅度差异最大.该汽车冷却风扇的工作点分布于ζ=0.06~0.12 区间(亦为最高效率区间),若在此区间内的气动性能变化幅值小于5%,则可以认为该非均布叶片方案对气动性能的影响很小.
冷却风扇噪声实验基于标致雪铁龙集团《热通风面板电动风扇总成标准技术规范》(B22 6310)分别对单风扇和风扇定子组合两种模式下的相关噪声进行测试,实验装置示意图如图10所示.首先,将矩阵中两个单风扇利用驱动器固定在夹具上进行噪声测试;然后,在风扇的下游添加定子静叶,并再次测试噪声.在半消声室中,转子的旋转轴线距地面的距离为 0.5 m,且旋转轴线与地面保持平行.传声器位于转子轴向距转子风扇轮毂 2.0 m、距地面 1.5 m处.所有转子风扇以 2 900 r/min (旋转频率为 48.3 Hz)的转速运行30 s,采样频率为 32.768 kHz.最后,在频率分辨率为1 Hz的条件下进行快速Fourier变换(FFT),分析结果如图11 和12所示,其中,SPL为声压水平.
由图11可见,相对于均布叶片(蓝色曲线)而言,非均布叶片(红色曲线)成功地调制了风扇噪声频谱中离散噪声的声学特性.均布叶片风扇噪声频谱中,H1(339 Hz)、H2(679 Hz)和H3(1 020 Hz附近)谐波分量是主要的离散噪声能量,其对风扇的声学特性有着重大影响.非均布叶片方案的风扇显著地改变了噪声频谱的离散特性,其H2和H3的谐波分量幅值大幅降低,能量向邻近阶次分散,但其H1基本保持在同一水平,这与图3中理论预测的趋势是相同的.同时,离散噪声的宽频背景水平亦有所提升(200 Hz~2 kHz),幅值最大处达到5 dB,这将使风扇的噪声总值陡增,本实验中噪声总值增加约 1.5 dB.虽然,非均布风扇的气动性能在自由空气状态下(图9中rs=0的位置)略有提升,但其变化率较小,不足以引起如此大的声学波动.故此处噪声增大的主要原因可能为叶片夹角的非均布设计改变了风扇的流场特性.
总之,叶片非均布设计成功地改变了转子风扇噪声频谱中离散能量在各阶次的分配比例,降低了谐波能量(H2和H3)的噪声水平,极大地改善了CFM的主观噪声舒适性.同时,叶片非均布设计也改变了风扇的流场特性,导致宽频噪声在局部频率区间有所增加,使得风扇噪声总值略有上升.但相对于主观舒适性的改善,噪声总值增加约 1.4 dB在总体上是可以接受的.
对于冷却风扇总成,设计合理的定子静叶不仅可以作为驱动电动机的支撑结构,而且可以改善离散噪声的性能.下文中的风扇总成设计是在同一个风扇、不同定子静叶分布情况下验证声学百叶窗效应.PR1与PR2同为均布叶片风扇,其静叶设计有所不同,前者为均布静叶,后者为百叶窗效应设计的非均布静叶.PR3与PR4、PR5与PR6、PR7与PR8的情况与之相同.
图5中的曲线分别为6静叶和8静叶方案中不同χ值对应的各阶次噪声水平相对值,其蓝色曲线(6静叶χ=0.2, 8静叶χ=0.3)在7阶次位置和靠近21阶次的位置出现波谷.对于7叶片风扇,从理论上而言,H1和靠近H3区域的谐波噪声将得到改善.图12的实验结果验证了该理论预测.与均布的静叶方案相比,H1(339 Hz)分别改善了 12.0,16.8,9.1 和 11.8 dB.同时,靠近H3(1 020 Hz)区域的谐波噪声也改善了1~3 dB不等.由图12还可以看出,对于相同风扇,调整χ仅影响离散噪声,而宽带噪声几乎保持不变.这种情况下风扇总成的总噪声水平将取决于离散噪声的波动.得益于H1的改善,均布叶片风扇噪声总值略有改善,而非均布叶片风扇的噪声总值水平则受到相关阶次波动的影响,其改善趋势不稳定.
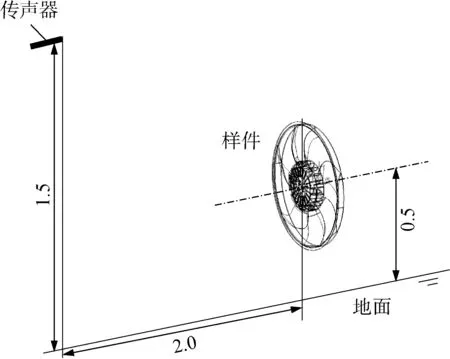
图10 噪声测试实验装置示意图(m)Fig.10 Noise test diagram (m)
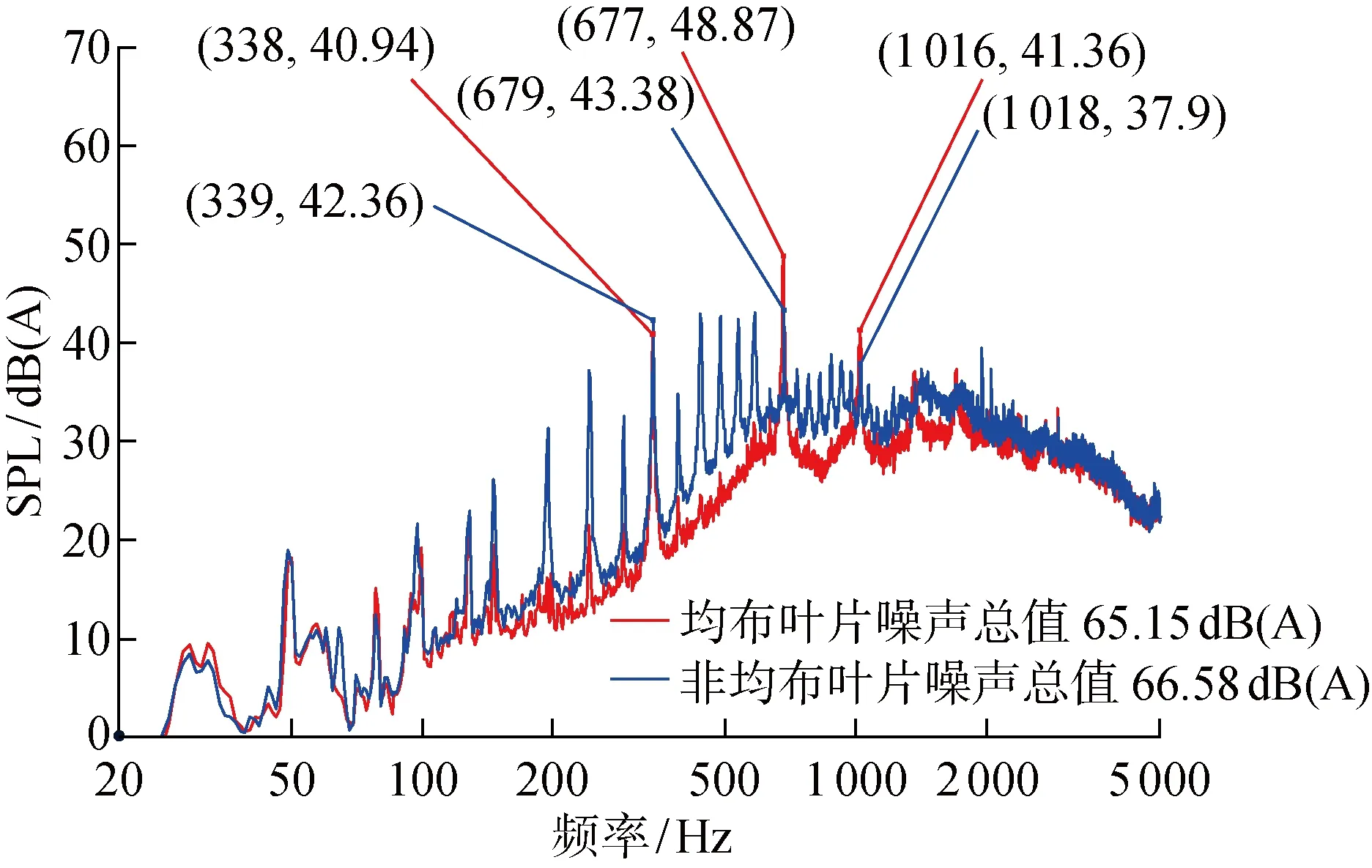
图11 单风扇噪声频谱图Fig.11 Noise spectrum of single fan
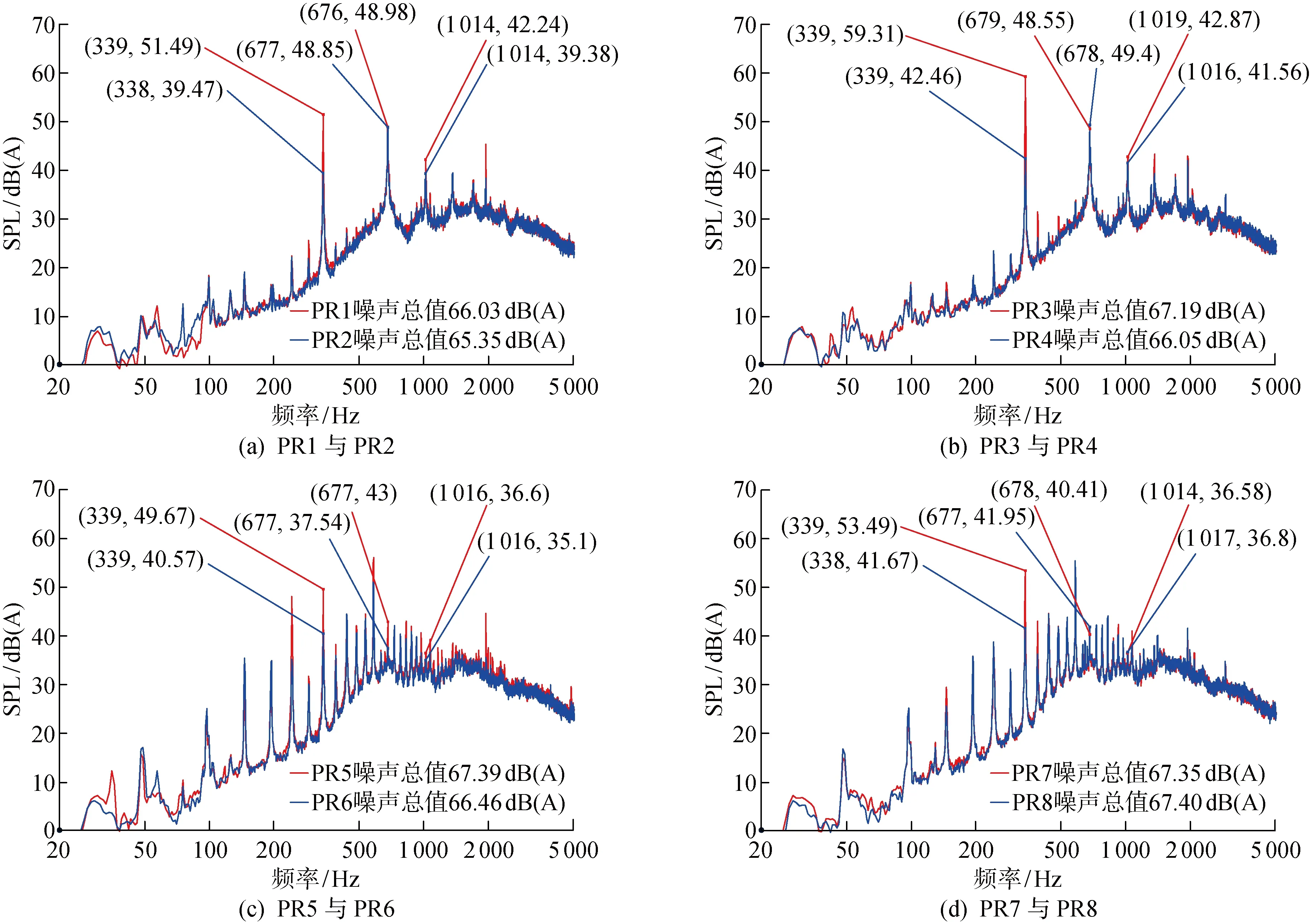
图12 噪声实验结果的频谱图对比Fig.12 FFT comparison of noise test result

表1 各方案的离散噪声水平Tab.1 Discrete noise level of each proposal
各种状态下的谐波噪声水平如表1所示.在当前测试条件下,可得如下结论:
(1) 静叶的排列方式对H1噪声水平的影响非常明显,在均布状态下效果最差,而基于本文的角度设计可获得较好的H1噪声水平;
(2) 与单风扇噪声频谱中H1的噪声水平相比,非均布静叶排列的H1噪声水平基本保持不变,而均布静叶排列极大地增大了H1噪声水平;
(3) 静叶排列的角度变化对H2噪声水平基本没有影响,对H3噪声水平的影响波动较小,在3 dB以内.
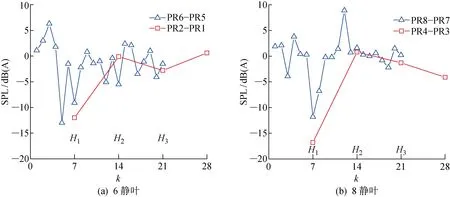
图13 离散噪声优化比较Fig.13 Distribution of discrete noise improvement
运用百叶窗效应设计后的6静叶和8静叶风扇总成方案的相关阶次噪声改善趋势如图13所示,其中,纵坐标表示非均布静叶定子阶次噪声改善水平的相对值.纵轴大于零的区域代表阶次噪声上扬,而纵轴小于零的区域代表阶次噪声得到抑制.图13主要绘制的是H3及以下谐波噪声的改善情况.一方面, 如前所述H1获得很大的衰减(9.0~16.8 dB),满足拟定的优化目标,H3附近也出现相同的降低趋势;另一方面,图5中理论推演曲线的波峰位置所展示的可能增强现象并没有在6静叶方案中出现,但在8静叶方案中的12阶次噪声有明显的增大.这说明在不同的静叶方案中,理论推测曲线的波谷对对应阶次噪声的抑制效果是比较显著的,而对波峰的影响会有所不同.在进行具体风扇总成优化的离散噪声设计时,要同时评估其他阶次可能出现的峰值,确认对总体离散噪声水平的影响,两者应相互平衡.
3 结论
本文从理论上探讨了相位调制原理在旋转机械(上游转子和下游定子)设计中的应用,提出了以A-χ方法预测旋转机械设计初期的离散噪声性能,并进行了气动性能和噪声水平的验证实验,以检验该方法在冷却风扇总成设计中的适用性和正确性,主要结论如下.
(1) 采用A-χ方法可使两种CFM的离散噪声性能均得到较大改善.在转子叶片调制原理的应用中,气动性能保持不变.
(2) 转子风扇设计中的参数A对宽频噪声有负面影响,但是可以对离散分量H2和H3等进行改善性调制.由于风扇模具制造中相邻叶片不能重叠,故叶片宽度限制了A的取值,进而限制了H1性能参数的优化.
(3) 根据声学百叶窗效应理论,定子调制参数χ在不影响其他噪声水平的条件下进一步降低了H1等谐波的离散噪声水平.在实际应用中,建议结合主观评估对离散噪声进行有效优化.
(4) 在冷却风扇总成的设计中,采用A-χ方法,可以在设计初期高效地控制风扇总成的离散噪声水平.
