小管径重力热管流动与传热特征的仿真研究

2019-05-08姚丽君

天津城建大学学报 2019年2期

姚丽君，张伟

（天津城建大学能源与安全工程学院，天津 300384）

在众多的传热元件中，热管是人们所熟知的最有效的传热元件之一，其利用工质相变，可将大量热量通过很小的截面积进行传输而不需外加动力.与其他传热元件相比，在运行过程中，热管的传热效率高，运行稳定，能够远距离地传递热量，并且传热阻力很低.因此，热管在能量传递方面具有明显的优势，其在余热回收[1]和太阳能集热器[2]等方面，均取得了良好的节能效果.

目前，国内外研究人员通过实验和理论分析对热管进行了大量研究，由于CFD（computational fluid dynamics）技术的日益成熟，大量研究人员通过建立与实验工况相同的仿真模型，很好地分析了热管内部复杂的汽液相变现象，为热管传热特性的分析和结构优化提供了有效的技术手段.

在热管内汽液两相流仿真方面，杨海滨[3]采用VOF模型，表面张力使用CSF模型计算，并耦合Lee模型实现了汽—液相间的相变，建立了蒸发管内两相流动沸腾数值模拟方法.Kuang等[4]分析了热管在低热功率下的传热特性，并分别对管内的流型：泡状流、弹状流和搅混流进行了CFD可视化分析，解析了不同质量流量对传热系数的影响.王啸远等[5]建立了CFD仿真模型，阐述了热管工质的蒸发和冷凝相变机理.Jouhara等[6]建立了重力热管的三维模型，对热管的间歇沸腾进行了数值模拟研究，分析了重力热管内复杂的多相流流动.

目前，对热管内汽液相变的研究大多以分析常规管径为主，对于小管径（毫米级）重力热管内相变行为的分析较少.在保证换热量的条件下，小管径热管比常规管径热管的管内比摩阻及摩擦压降大，但传热系数也大，因而经过优化计算，可使工质压降与热管传热性能实现优化，同时选用小管径热管能够提高换热效率，并且可以降低制造成本.本文将对小管径（内径为6.8 mm）热管内的汽液相变行为进行CFD可视化，分析其汽液流动特征.

1 物理模型

建立小管径重力热管的二维物理模型，其尺寸与文献[7]中的实验物理模型相同（见表1）.

表1 热管物理模型基本参数mm

2 数学模型及数值计算方法

2.1 VOF模型

2.1.1 连续性方程

连续性方程公式如下

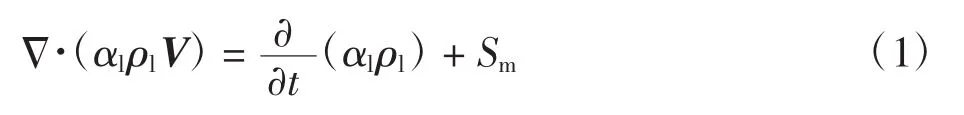
式中：αl为液相体积分数；ρl为液相密度；V为速度矢量；Sm为质量源项，其用来计算在蒸发和冷凝过程中的质量传递.

在VOF模型中汽相和液相体积分数之和为1，即

式中：αv为汽相体积分数.

2.1.2 动量方程

在动量方程中，引入了由Brackbill等[8]提出的连续表面张力模型（CSF模型）添加至动量源项中，形成动量源项的表达式

式中：σ为表面张力系数；Cv为汽相表面曲率；Cl为液相表面曲率.

考虑到重力、压力、摩擦力和表面张力联合作用到汽液交界面处.因而，VOF模型的动量方程形式如下

式中：g是重力加速度；p是压力；I是单位张量；μ是动力黏度.

2.1.3 能量方程

能量方程为

式中：E为内能；k为有效导热系数；SE为能量源项，用来计算蒸发和冷凝过程中的热量传递.

2.2 蒸发冷凝模型

根据Schepper等[9]提出的关于蒸发冷凝过程的数学描述，获得蒸发和冷凝过程的质量和能量源项方程，并通过用户自定义函数（UDF）将汽液相质量和能量源项加载至FLUENT中，实现蒸发和冷凝过程相变的平衡.

当T≥Tsat时为蒸发过程

当T＜Tsat时为冷凝过程

式中：ΔH为汽化潜热；Tsat为饱和温度；Sm，l和Sm，v分别为液相和汽相的传质量.

通过引入两个质量转移时间松弛因子β1和β2来分别表示蒸发和冷凝过程热质传递过程，其大小反映了蒸发和冷凝的速率.本文β1和β2均取0.1时模拟具有良好的收敛性.

2.3 网格及边界条件

运用Gambit软件对重力热管进行网格划分，网格类型为四边形网格，共有34 982个网格.图1为热管的网格图，其中图1b为网格的局部放大图.本文对热管内壁面建立了边界层网格，用于捕捉沿管壁的汽液相变现象.

由实验工况确定管内运行压力为7.45 kPa，即管内真空度为93.88 kPa.根据实验，蒸发段加热功率恒定，由此在FLUENT中蒸发段采用恒热流密度边界条件，绝热段不与外界进行热交换，边界条件设定为热流密度为0，冷凝段采用水冷的方式进行冷却，边界条件设定为对流换热，不同条件下的对流换热系数与实验条件一致.

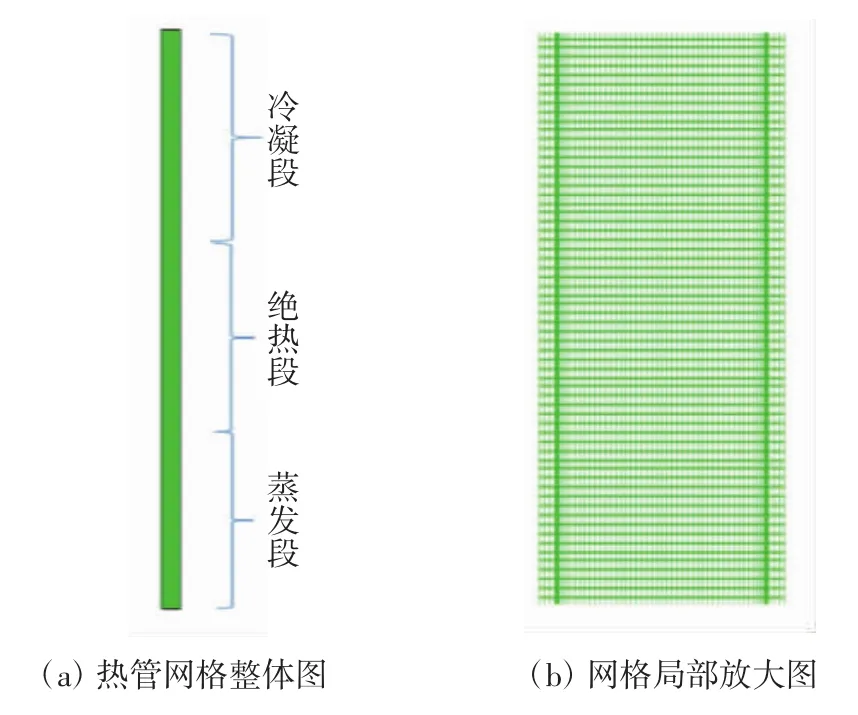
图1 热管二维网格图

2.4 仿真求解方法

本文选用多相流模型中的VOF模型，时间步长设定为1×10-4s，并运用PISO算法计算压力-速度耦合项，设定压力离散格式为PRESTO，界面体积分数采用Geo-Reconstruct插值算法.

3 数值计算结果及分析

3.1 模型验证

加热功率为80 W，充液率FR（蒸发段液态工质与蒸发段容积的比值）为50%的工况下，在热管蒸发段、绝热段和冷凝段共建立与实验位置相同的9个测点，用以与实验各段测点温度的比较.表2为热管不同位置模拟与实验温度误差分析表，从表2比较分析可得出：蒸发段的平均误差为2.79%，绝热段的平均误差为8.64%，冷凝段的平均误差为6.47%.由此可以看出仿真与实验结果的吻合度较高，验证了本文仿真传热模型的可靠性.从各段温度值中可以得出，绝热段和冷凝段温度的仿真值均比实验值大，这是由于实验装置中绝热段存在局部散热损失以及冷凝段可能存在不凝性气体造成的.

表2 各测点模拟温度与实验温度值比较℃

3.2 传热性能分析

热管的运行热阻是评价热管传热性能的一个重要因素，反映了热管传热速率的快慢，热管的运行传热热阻计算公式为

式中：Te，av为蒸发段平均温度；Tc，av为冷凝段平均温度；Qin为热管输入功率.

图2分别给出了热管在不同加热功率和倾角下的传热热阻.从图2a中可以看出：当充液率FR=50%时，随着加热功率的增加，热管的传热热阻在加热功率为20～90 W时先减小后增大，同时可以看出加热功率为40～70 W时热管的传热性能较好.这主要是由于加热功率的增加使得热管蒸发段壁面过热度增加，继而使得蒸发段产生的蒸汽速率加快，由此对液池内液相工质的扰动不断增强，从而加速了蒸汽到达冷凝段，一定程度上提高了蒸汽释放汽化潜热的能力，在此过程，使冷凝段平均壁温得以升高，进而传热热阻降低.

但加热功率的持续增加，会使热管蒸发段表面平均热流密度不断增大，由于管径较小，在热管的汽液相变过程中，蒸发段汽液相变速率很快，致使大量的蒸汽流涌向冷凝段，而形成的冷凝液膜在未回流至蒸发段就已被蒸干.因此，液膜的回流受阻使得蒸发段出现液相工质的补给缺失，使得蒸发段传热出现恶化，进而使得管壁温度骤然升高.另外，在充液率一定的情况下，其释放汽化潜热的能力也是有限的，尽管提高了加热功率但冷凝段平均温度仍保持在一定的范围之内，从而使得热管蒸发段和冷凝段的温度相差甚多，导致热管的整体传热热阻出现增大的趋势.

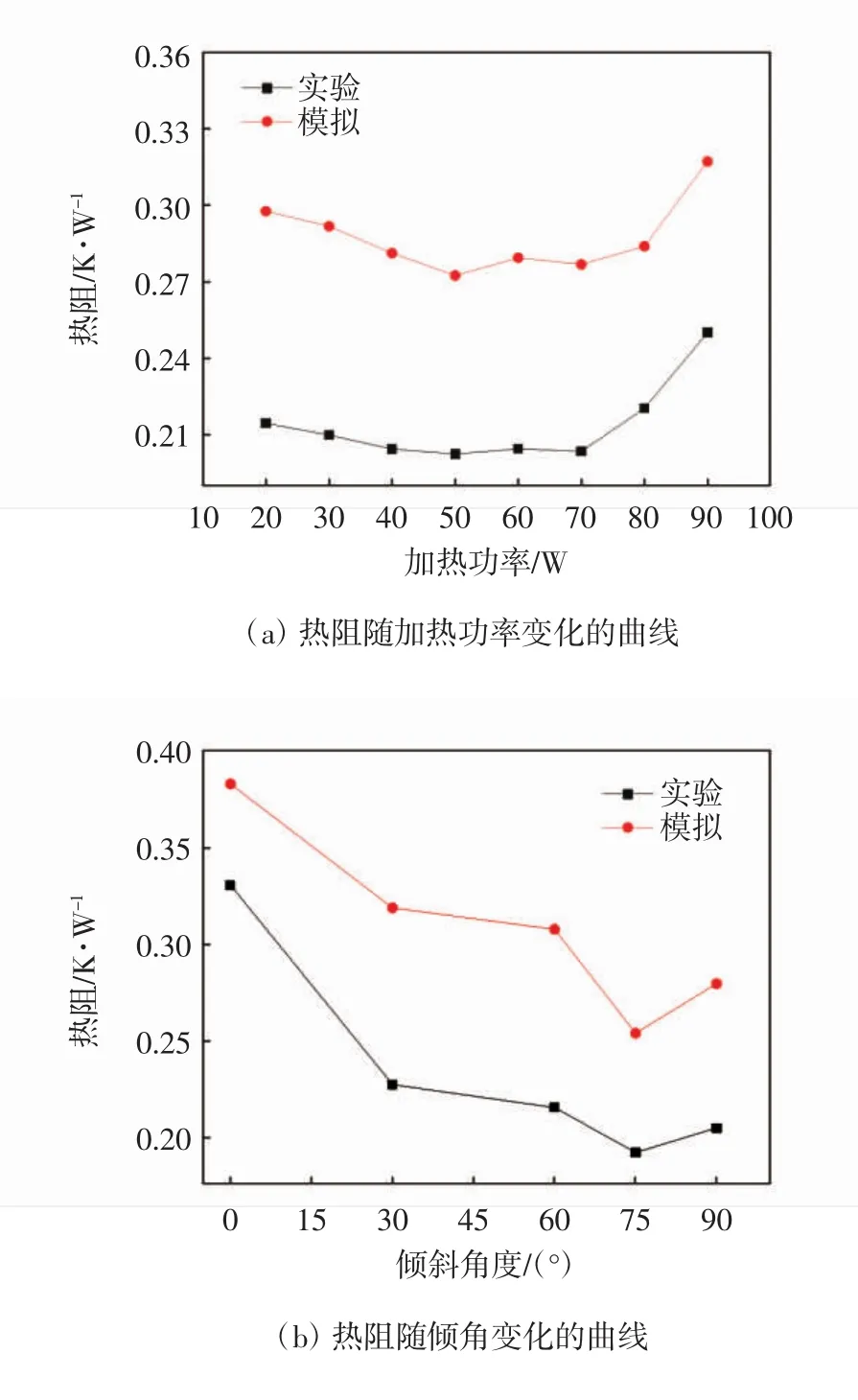
图2 加热功率和倾角对热阻的变化曲线

由图2b中可以看出：在加热功率为60 W时，随着热管倾斜角度的增加，热管的整体热阻先减小后增大.当热管倾角为0°时，蒸汽到达冷凝段形成的冷凝液无法及时地补给到蒸发段，冷凝液聚集在管底部使得液膜厚度增加，增加了冷凝段传热热阻，从而降低了冷凝段的对流换热能力，使得热管的轴向温差增加.随着倾角的加大，管内出现了汽液分层现象，使得汽液相间剪切作用力减小，因而使冷凝液的回流动力得以提高.本文中，当倾角为75°时，热管的传热热阻达到最小，热管的传热性能较好.当倾角为90°时，汽液处于逆向流动，由于管径较小，使得汽液交界面处的剪切力较大，冷凝液回流受到阻碍，导致传热热阻增加.

3.3 汽液流动CFD可视化

图3给出了热管在加热功率为60 W，充液率FR=50%，倾角为90°时，蒸发段不同时间汽相体积分数云图，从图3中可以清晰地看出：①随着热管壁面热流密度的增加，蒸发段壁面和液池内产生了汽化核心，随着热量的不断输入，汽化核心数逐渐增加，其演变成小的气泡，形成泡状流.②随着相变现象的进行，截面含汽率不断增加，从图3中可以清楚地观察到管内小汽泡的生长、脱离、聚合以及汽泡从液池的逸出等动态过程，在此过程，由于管径较小，会形成与管径相当的帽状气泡，帽状汽泡聚合形成泰勒大气弹（弹状流）.③随着相变现象的进一步发展和演化，会在管内形成局部的蒸汽区，此时蒸发段出现局部高温，对流换热系数降低，传热性能出现恶化.

图3 蒸发段不同时间汽相体积分数云图

图4a为热管在达到稳定运行后冷凝段液膜的分布图，从图4a中可以清楚地看出液膜沿管壁内侧基本呈均匀分布，而在下端液膜厚度略高于中上部液膜厚度.图4b为不同时间冷凝段局部的液膜流动汽相体积分数云图.由图4b可知，随着汽液相变现象的进行，冷凝段的液膜逐渐呈均匀分布，并且液膜厚度由薄变厚.这是由于蒸发段产生的蒸汽在上升至冷凝段的过程中，会在冷凝段壁面形成一层很薄的雾状薄膜，由于表面张力和重力的联合作用，使液膜逐步向下流动，随着蒸汽流量的增加，其释放汽化潜热后形成的冷凝液随之增多，冷凝液将更多地附着至管内侧，因而液膜厚度也随之增厚.