基于动态强度折减DDA法的边坡多滑面稳定性分析

王述红，朱承金，张紫杉，任艺鹏,王鹏宇，邱 伟

(东北大学 资源与土木工程学院，辽宁 沈阳 110819)

高边坡由于具有规模大、地质条件复杂、易受周边环境干扰而破坏失稳的特点，在初次失稳后易发生二次失稳，形成次级滑动面。岩质高边坡受层理结构的影响，使得边坡的稳定问题更加复杂和突出，故对潜在多滑面的岩质高边坡稳定性进行深入探究任重而道远[1-3]。

边坡稳定性分析中有2种常用的计算方法:极限平衡法(LEM)[4]和有限元法(FEM)[5]。与有限元相比，极限平衡法计算效率高，通过几何假定并基于已知或假定的规则滑面求解安全系数，但其忽视了边坡滑落过程中岩土体的本构关系[6]。近年来有限元快速发展并将强度折减法结合，该技术不必预先假设滑动面的位置，且易得安全系数及相应潜在滑动面，其局限性在于安全系数及滑动面求解的单一性。CALA等[7]开创了新型强度折减法，在常规方法基础上得出最危险失稳面，进而确定首次滑落的步数Nr，继续增大折减系数，随即1.1Nr步将会被计算，相继求得对应次级潜在失稳面及安全系数。李小春等[8]利用检索边坡体单元的方法，对不同折减系数下各范畴边坡单元进行统筹，以此得到多个滑落面及相应安全系数。

非连续性是岩体固有的属性，由SHI[9]首次提出的非连续变形分析(DDA)在模拟块体大位移、大变形方面独具优势，在边坡工程领域也得到迅速发展。MACLAUGHLIN等[10]模拟了倾斜边坡的平面和弧形破坏模式，发现其结果比常规分析方法具有更好的精度。FU等[11]将矢量和方法(VSM)应用到DDA中，基于实际应力状态和矢量和算法计算边坡稳定安全系数。

发展边坡稳定性评价核心问题在于安全系数及相应滑落面的求解。过去研究中的强度折减法大都是对岩体统一折减，在实际情况下，主要是结构面的力学性质决定了岩体的力学性质，且岩体结构面破坏时并不是同时损伤同等程度;再之边坡首次发生失稳后块体位置及应力已重新分布，故应使用首次失稳结束后的边坡模型对次级滑落面进行分析，而以往对边坡次级滑动面的研究中鲜有考虑该实际状况。为了解决该问题，笔者借鉴DDA计算位移的优势，考虑块体间相对位移，提出基于DSR-DDA法的边坡多滑面搜索并进行边坡稳定性评价，利用倾斜平面滑块经典案例测试位移阈值，验证方法的可行性及计算精度，并尝试将其应用到抚顺西露天矿岩质高边坡的稳定性分析中。

1 DSR-DDA法

1.1 DDA基本原理

DDA利用一阶位移函数来表述每个块体的运动参量，并假设应力和应变是恒定的[12]。每个块体的位移矢量包含6个变量:

D=(u0,v0,r0,εx,εy,γxy)T

(1)

其中，(u0,v0)为块体内特定点(x0,y0)的刚性位移;r0为块体绕特定点(x0,y0)的旋转角度;εx,εy,γxy分别为该块体的正应变与切应变。块体内任意点(x,y)的位移(u,v)为

(2)

基于最小势能原理构建的系统整体平衡方程为

(3)

式中，系数矩阵中Kij为6×6子矩阵;Kii由块体单元的材料属性和几何参数决定;Kij(i≠j)则由块体i和块体j间的接触条件而决定;[Di]和[Fi]为6×1子矩阵;Di为块体i的变形变量(d1i,d2i,d3i,d4i,d5i,d6i);Fi为块体i上分配给6个变形变量的荷载。

1.2 DSR-DDA法位移阈值

为了考虑真实情况中块体结构面损伤的程度不一性，提出对位移变化不小于阈值的块体结构面剪切强度进行折减变化，利用经典斜坡滑块案例测试剪切强度折减的位移阈值，模型如图1所示，岩体参数见表1。在程序计算中，块体结构面抗剪强度参数每隔一定时步(10 000步，每一时步为0.001 s)按照块体相对位移变化与阈值的关系只针对位移变化符合要求的结构面进行折减，折减系数从1.000开始，依次增加0.001，直至发生急剧变形，则此时其取值为该边坡滑落面安全系数。该程序计算所模拟的折减过程在一定程度上与实际情况下岩体材料的损伤退化相符。

图1 滑块沿斜坡滑动模型Fig.1 Model of sliding block along slope

该简易模型运动问题安全系数解析解为

(4)

该算例结构面选取各内摩擦角对应解析解值见表2。图2为结构面内摩擦角φ取不同值下，模型安全系数及安全系数与解析解的误差百分比随位移阈值的变化曲线，由图2可得，不论内摩擦角φ取何值，当位移阈值接近1 mm时，安全系数取值接近最大值，且与解析解的误差百分比有一个明显的凹槽，说明这时的误差与解析解相对最小且在0.5%以内，所以位移阈值暂时取为1 mm，与解析解的结果保持一致。从而说明了DSR-DDA法是满足计算要求的，并且能保证一定的计算准确性。

表1 边坡模型岩体参数Table 1 Mechanical parameters of the slope model

表2 安全系数解析解Table 2 Theoretical safety factor

图2 安全系数及其误差随位移阈值变化曲线Fig.2 Curves of safety factor and its error with displacement threshold

块体间接触力的精确求解是解决总平衡方程的核心步骤。在每一时步内，都要重新确定弹簧的施加与否及弹簧的位置，需要反复生成求解总刚度矩阵，刚性弹簧的施加与去除过程称之为开-合迭代。接触有3种状态:张开、滑动和锁定。模式变化的判定准则见表3，其中，N为法向位移，N>0为张开;t为剪切位移矢量;f为摩擦力矢量；T为剪切位移;‖为两个矢量方向相同。

基于以上分析，DSR-DDA法在程序中实现如图3所示。

表3 接触状态Table 3 Contact status

图3 DDA程序步骤流程Fig.3 Flow chart outlining the procedures of the DDA

图4 边坡全貌及地质剖面Fig.4 Slope topography and geological section

2 抚顺西露天矿岩质边坡模型及参数

2.1 抚顺西露天矿岩质边坡概况

露天开采在煤炭资源开采中占据至关重要的地位[13-14]。抚顺西露天矿地处抚顺市中心，其边坡稳定性直接决定了矿坑与城市交界处的安全与否。由于受到浑河断裂的牵引作用,向斜北翼地层遭受了强烈改造和破坏。向斜轴部呈圆弧型褶曲,轴面呈现曲面状,向北倾斜,倾角30°左右轴迹方向为NE60°,长为20 km,两翼间距为3 km。北翼产状各异,倾角15°～60°,间或伴有小型褶曲。目前,采坑北帮边坡滑坡、崩塌、地裂缝等地质灾害仍持续不断，不时产生大型滑坡。故选取北帮W区某标段岩质高边坡作为案例。图4为该标段边坡全貌及地质剖面图，为监测边坡实时位移，在钻孔中布置深部位移测斜仪。

2.2 计算分析模型及参数

图5 UAV技术Fig.5 UAV technology

节理、裂隙等不连续结构面对岩体的变形起到控制作用，结构面信息采集精度对数值模拟分析准确性至关重要。运用高精度、高效率的UAV(图5)技术对确定性结构面信息进行非接触精准获取，生成点云模型。假定结构面平面方程为

D=AX+BY+C

(5)

其中，A，B，C，D为结构面平面参数，提取结构面所在平面的法向量n=(-A,-B,1)，并对结构面进行点的拾取，可得

(6)

借助最小二乘法解(A，B，C)，结构面倾向及倾角分别为

(7)

式中，α，β分别为结构面倾向和结构面倾角。

对结构面产状进行计算，并对提取出的结构面产状信息导出，部分计算结果见表4，结构面产状统计云图如图6所示。

研究表明结构面产状服从一定规律分布，对确定性结构面分组处理，并依照双正态密度分布生成随机结构面产状，其标准变化形式为

(8)

式中，σα为确定性结构面倾向的标准差;σβ为确定性结构面倾角的标准差;ρ为结构面倾向、结构面倾角的相关系数;μα为确定性结构面倾向的均值;μβ为确定性结构面倾角的均值。

表4 产状计算结果Table 4 Yield calculation results

图6 结构面产状统计云图Fig.6 Statistical cloud chart of structure surface

将获取的结构面信息导入DDA程序中，结构面网格切割岩体，形成DDA的块体单元，即算例数值计算分析模型(图7)。

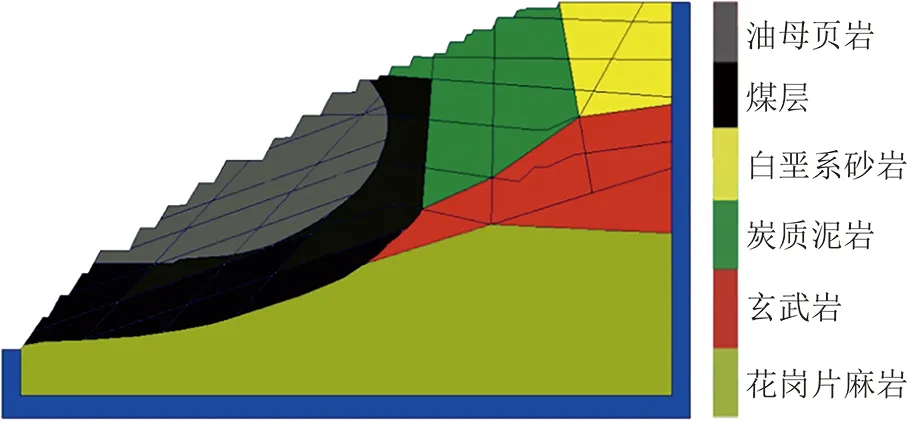
图7 抚顺西露天矿北帮边坡DDA数值计算分析模型Fig.7 DDA numerical calculation and analysis model of slope in West Fushun Open-Pit Mine

天然应力场仅将重力作用纳入范围，不计算区域构造应力影响。根据地质勘探和试验成果，得表5所示各项参数。程序计算中，块体结构面抗剪强度参数每隔一定时步(10 000步，每一时步约为0.001 s)针对块体相对位移变化达到或超过位移阈值的结构面进行折减，折减系数从1.000开始，依次增加0.001，在一定程度上与实际情况下岩体材料的损伤退化相符。

表5 边坡模型岩体参数Table 5 Mechanical parameters of the slope model

3 抚顺西露天矿岩质边坡稳定分析

3.1 现场位移监测及数值计算分析

测斜孔布置参考图4，测点间隔为1 m，近2个月内各测斜孔不同深度测得的累计位移值如图8所示。

图8 测斜孔测点累积总位移值Fig.8 Cumulative displacements of monitoring point in surveying slant hole

分析图8可得，测斜孔69002内前100 m左右测点总位移值随时间增长变化极大，且在深度为100 m附近存在位移值剧增，说明测斜孔附近岩体已发生相对滑移，并有继续滑动的趋势，且滑动面在距坡面100 m附近。测斜孔55026内前20 m左右测点总位移值增加相对迅速，且存在继续增长的趋势，后续测点位移变化效果不明显，且趋于稳定，推测该测斜孔上部岩体存在个别不稳定块体。测斜孔74003内测点位移随时间增长较慢，无明显规律且趋于稳定，说明暂时该区域岩体稳定性较好。

为进一步确定边坡潜在滑落面位置，根据DSR-DDA法，动态折减抗剪强度参数，对边坡渐进失稳过程进行表征，并给出滑落面与相应的安全系数。选取该边坡最危险滑落面与次级滑面验证了方法的可行性，图9～10为边坡首次失稳与二次失稳过程。

第1.360×106时步前，各块体监测点位移及边坡整体基本保持平稳状态，当运算至第1.360×106时步时，即折减系数达到1.136时，边坡发生急剧变形，相应块体位移激增，且后续变形亦呈逐步增加趋势，并且从边坡整体变形中可以明显看出下部滑坡体沿相应滑落面发生滑移，说明边坡发生首次失稳，最危险滑落面所对应安全系数为1.136。

边坡首次失稳结束后，块体位置及内部应力重新分布。运用首次失稳过程结束后的边坡模型继续运行程序，旨在寻找次级滑落面。

图9 抚顺西露天矿北帮边坡首次失稳过程Fig.9 First failure process of the north slope in West Fushun Open-Pit Mine

图10 抚顺西露天矿北帮边坡二次失稳过程Fig.10 Second failure process of the north slope in West Fushun Open-Pit Mine

第1.890×106时步前，边坡整体趋于稳定，当运算至第1.890×106时步时，即折减系数达到1.189时，边坡再次发生急剧变形，形成次级滑落面，其对应安全系数为1.189，且较首次边坡失稳其滑落面范围更大，而且是在首次失稳发生后边坡强度略微减小后，与常规分析得出的结果大相径庭(常规分析中不能剥离首次失稳滑坡体，导致其对二次滑坡体起到保护作用，从而计算得到的安全系数偏高)。究其主要原因是边坡首次发生失稳后块体位置及应力已重新分布，故应使用首次失稳结束后的边坡模型对次级滑落面进行分析，而以往研究中并未充分考虑这一因素。

抚顺西露天矿边坡案例破坏模式为牵引式滑动破坏，中下部油母页岩对边坡稳定性起关键作用，故不可继续开采剩余油母页岩，以免引起边坡上部大面积滑坡及矿坑-城市边界滑坡。

3.2 DSR-DDA法与GeoSMA-3D耦合

GeoSMA-3D(岩土工程结构与模型分析系统)是一款以Key Block Theory为基础，在C++框架下编译源程序，团队研发的三维关键块体可视化分析软件。该软件能实现工程岩体空间结构的建模、结构面的空间表征、模型表面迹线显示等多项功能，并且其精度已经过大量实例验证[15-17]。

将结构面产状导入GeoSMA-3D软件，完成关键块体搜索过程，并实现其三维表征;DSR-DDA法中最先发生滑落的块体即为关键块体，关键块体耦合如图11所示，且耦合效果良好。

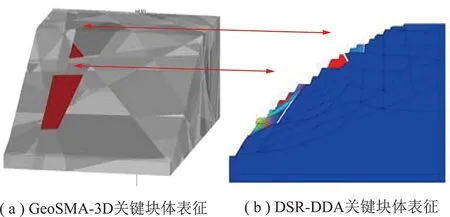
图11 关键块体耦合Fig.11 Key block coupling

4 结 论

(1)提出了受位移阈值控制的DSR-DDA法，给出了DSR-DDA法计算边坡多滑面安全系数的基本过程，为边坡多滑面稳定性分析贡献了一种新手段。

(2)利用经典斜坡滑块案例验证了DSR-DDA法的可行性与计算精度，并给出了位移阈值为1mm，对不同破坏程度下岩体结构面动态折减不同的强度，解决了数值分析中岩体结构面损伤的程度不一性问题。

(3)基于DSR-DDA法分析了抚顺西露天矿北帮边坡多滑面稳定性，得到了其最危险滑落面及次级滑落面位置，与常规分析结果大相径庭，佐证了边坡多滑面稳定性分析中模型需动态变化的必要性。该边坡破坏模式为牵引式滑动破坏，中下部油母页岩对边坡稳定性起关键作用，故不可继续开采剩余油母页岩，以免引起边坡上部大面积滑坡及矿坑-城市边界滑坡。

致谢衷心感谢石根华博士对笔者的热忱帮助。