八光子纠缠态制备方案

李婷玉，李 晖

（沈阳工业大学信息科学与工程学院,沈阳110870）

1 引言

量子通信是量子力学与经典信息科学的交叉学科，是量子物理与计算机科学相结合的新研究领域。作为量子信息学的核心部分，量子纠缠更是广泛的应用于量子信息处理中。纠缠态实质上就是多子系量子体系中的一种不可分离的态[1]，揭示了量子力学的非局域性。作为量子通信中的量子信息传输通道，也广泛被研究于纠缠态的制备、纠缠源的分配以及纠缠态的操纵等方面。几十年来量子通信领域对于纠缠态的制备进行了大量的研究，通过不断的实验和应用，产生了很多简便、高效的制备方法。潘建伟小组首次在实验上完成三光子GHZ态的制备[2]，在该方案中使用了两对纠缠光子对，得到两种情况的三光子纠缠态，把这两种情况相干叠加，得到三光子GHZ态。Walther P等在实验上首次制备出了四光子簇态，并利用它对one-way量子计算方法进行了验证[3]，这在光量子信息处理上是非常有意义的。丁东等提出了一个用三对纠缠光子制备六光子超纠缠态制备方案[4]，实现了对包含偏振纠缠和空间纠缠的六光子超纠缠态的制备。徐凭对传统的两光子极化纠缠态的制备过程加以改进，并成功地利用八个光子的极化态制备了八量子比特GHZ态[5]。

随着纠缠光子数的增多，纠缠态的制备难度呈指数增加。目前，在离子阱、原子-光腔、自发参量下转换等多种体系中都已经实现了实验上的纠缠制备，其中以自发参量下转换体系中产生光子纠缠态的方案较为简单易行。自发参量下转换是一种非线性光学过程，是指一束短脉冲紫外光子入射到非线性晶体BBO（Beta-Barium Borate）上产生两个纠缠光子的现象[6-8]，对应的这两个光子分别称为信号光子和休闲光子。该方案的优点在于操纵简易，但也同时存在着效率不高的缺点，不适合用于高亮度的纠缠态。自发参量下转换过程分为两类，第一类中产生的信号光子和休闲光子的偏振方向相同，在第二类中产生的信号光子和休闲光子的偏振方向互相垂直。

故此考虑由二型自发参量下转换源产生四个独立的双光子纠缠态的情况，通过使用由几组偏振分束器、半波片等线性器件组成的量子线路演化双光子纠缠态，提出了一种八光子纠缠态的制备模型，不仅体现了对八光子纠缠态的观察，而且对八光子纠缠态的保真度进行表征，得到八光子量子态保真度与信道系数比之间的关系。

2 八光子纠缠态的制备

在本方案中，由一个来自锁模的钛蓝宝石激光器的短（约200fs）紫外光脉冲通过一个光学非线性晶体（BBO）产生成对的纠缠光子。在每个脉冲中产生纠缠光子对的概率很低，约为10-4量级。在此情况下产生的纠缠光子对的偏振纠缠态为：

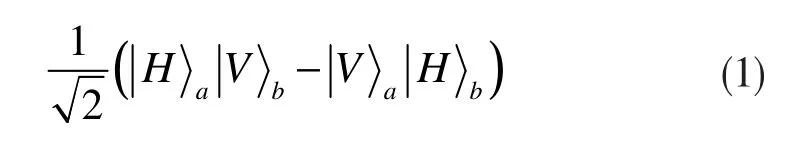
这种状态表明同时存在着光路a1中的光子水平极化及光路b1中的光子垂直极化的可能性为相反的可能性为，减号表示两种可能性之间存在固定的相位差为π。

对于我们的纠缠态实验模型，这个相位因子允许具有任何值，只要它对所有制备的纠缠对都是固定的。

这种设定使得在光路a1中的光子继续朝向偏振分束器，其中H光子沿着e1，V光子将始终以10-5误差率被反射沿着光路E1传输。与此同时，将激光器入射后未被转化的激光使用凸透镜进行增强，并由平面镜反射至第二块BBO晶体，使得光路在a3中传输，并继续朝向偏振分束器，其中垂直（V）光子沿着e2，水平（H）光子朝向光路E2传输并与E1中的光子一起被引至偏振分束器，调整每个粒子的路径长度，使它们同时到达。本方案中，在所有的输出光路中使用八个光纤耦合单光子计数器（D1,D2,D3,D4,D5,D6,D7,D8）计数，光子的总收集和探测概率约为10%。滤波过程的相干时间要远大于泵浦脉冲持续时间，这样可有效消除根据它们的到达时间区分两个光子而导致干扰的任何可能性。在相关电路中只提取所有八个检测器在几ns的小时间窗内记录光子的符合事件。此举的必要性在于排除泵浦脉冲在某一侧泵浦晶体中产生一对或两对纠缠光子，而在其它侧泵浦中却没有产生光子的情况。

3 理论推导

本方案的研究是基于二型自发参量下转换过程制备八光子纠缠态的方案。制备原理如图1所示。

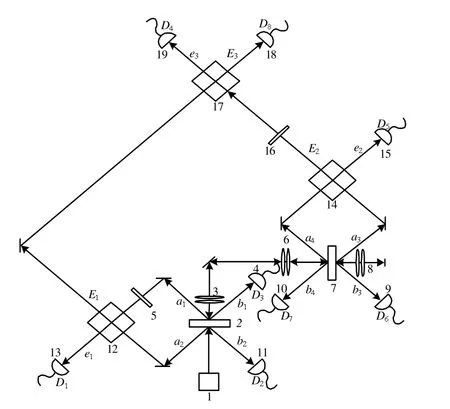
图1 八光子纠缠态的制备原理图

考虑一个短脉冲紫外光通过BBO晶体，使用四个独立创建的光子对。再两两一组分别组合在一起，每一组中的两个独立创建的纠缠光子对各提供一个纠缠的粒子对。偏振分束器再各自提取一个粒子组合在一起。在其输出端口中检测到的两个光子都是H（水平）或者都是V（垂直）偏振[9]，从而将获得完整的四光子纠缠态，再与另一组中获得的四光子纠缠态重复上述操作，即可获得完整的八光子纠缠态。

假设在第一步反应中四对纠缠光子处于如下状态：

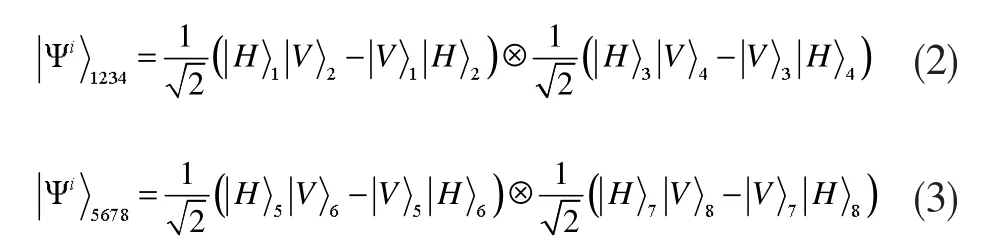
这8个粒子分别为两个极化纠缠光子对的张量积，其中H(V)表示水平（垂直）偏振光子状态。每对中的一个光子被引导到偏振分束器（PBS）的两个输入端。由于PBS的特性是水平偏振的光投射，而垂直偏振的光反射，所以意味着两个PBS输出端的结果a1和a2要么都是水平偏振的，要么都是垂直偏振的；同理，光子a3和a4都是水平偏振或者都是垂直偏振的。因此将公式(2)、(3)表示的量子态投影到了一个二维子空间上：

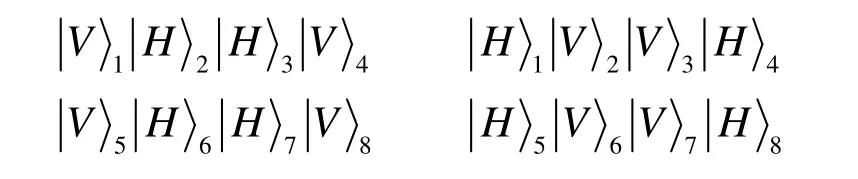
在四对纠缠光子对分别经过两块PBS以后的状态为：

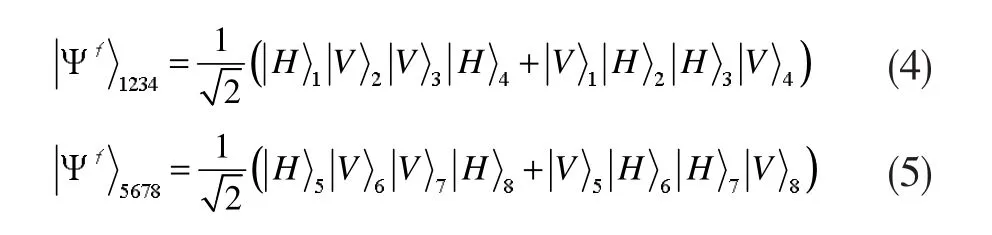
此时，这是一个四个粒子的GHZ状态，再将制备得到的两对四粒子GHZ态经过PBS后，得到状态为：

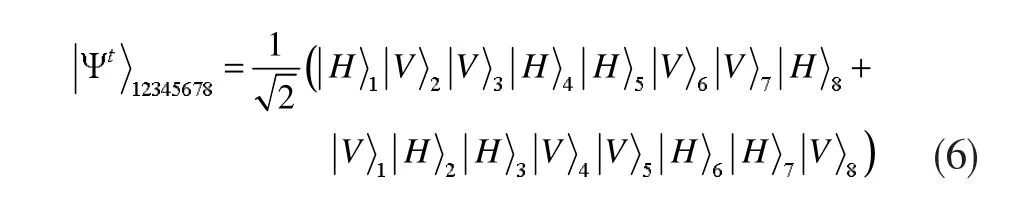
此时产生一个八粒子GHZ态，根据GHZ定理，它可以表现为非局域行为。

4 八光子纠缠态保真度

为方便起见，将公式(6)表示的要传输的八光子纠缠对表示为：

传送八粒子的EPR信道分别由粒子组成，且信道表示为：

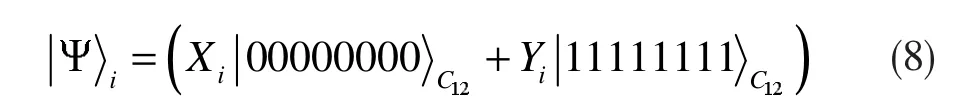
式中Xi、Yi为信道系数，其幅度满足：

式中，i表示第i对EPR信道；下角标Ci1、Ci2分别表示组成第i个信道的纠缠粒子对中的第1个粒子和第2个粒子。

信道系数幅度满足：

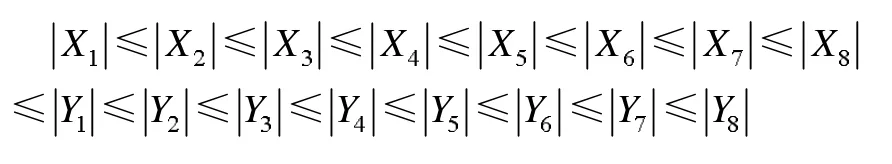
总的量子系统表示为：

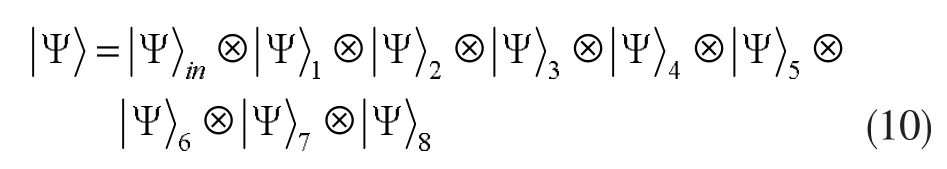
对八光子纠缠态进行Bell测量，在测量结束后，由纠缠特性得到传输后的量子态，该量子态的密度矩阵为：

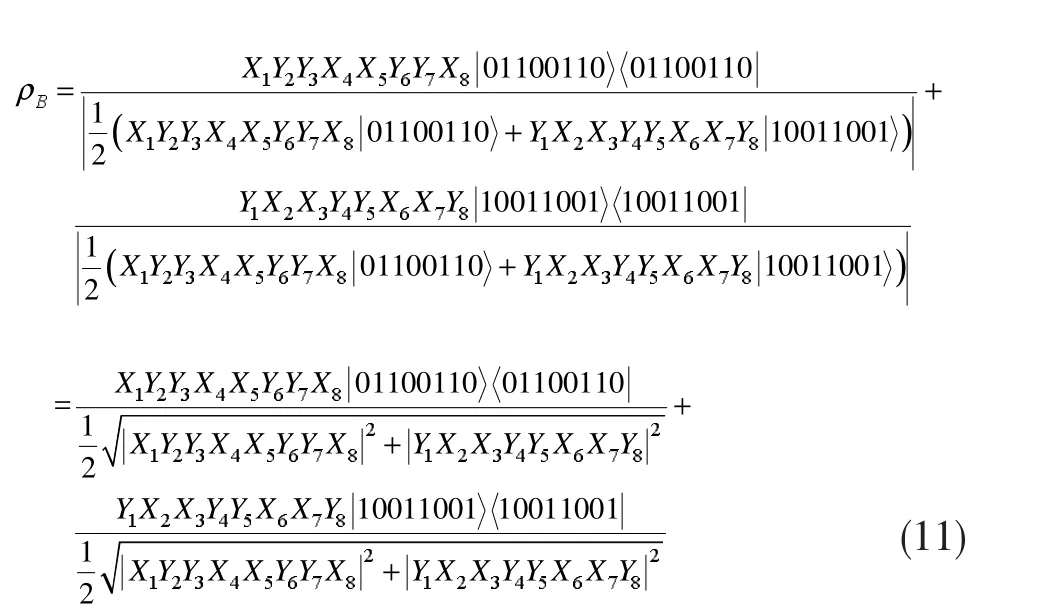
经过幺正变换后量子态的密度矩阵为：

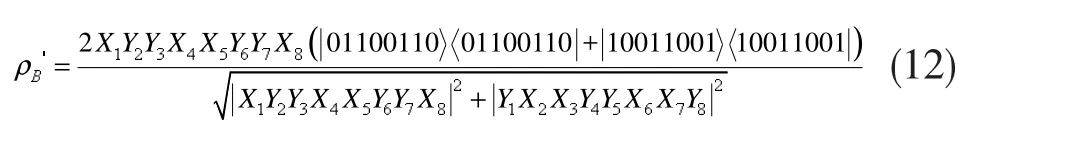
将式（12）带入保真度的数学模型为：

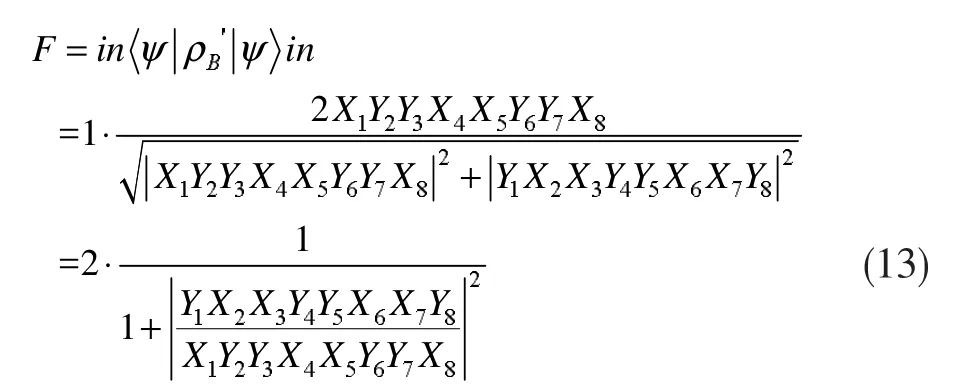
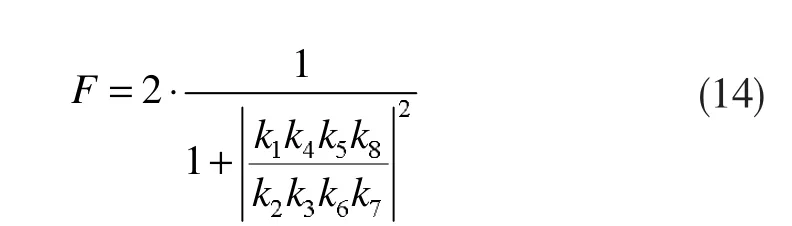
当k1=k2=k3=k4=k5=k6=k7=k8=1时，保真度最大，即F=1，表明此演化推导方式是正确的。同样可对保真度与纠缠信道系数取值之间的关系进行定量分析，经典信道所能达到的最大保真度临界值为0.6700[10]，所以当保真度大于0.6700时，八光子量子态的隐形传输成功，否则隐形传输过程失败。

由式(14)可知，信道系数幅度比k1和k4、k5、k8对保真度以及信道整体的影响是相同的。同理，信道系数幅度比k2和k3、k6、k7对保真度以及信道整体的影响也是相同的。故此用K1来表征k1k4k5k8的变化趋势，用K2来表征k2k3k6k7的变化趋势，得到八光子量子态传输时保真度随信道系数幅度比的变化曲线，如图2所示。与信道系数幅度比之间的关系进行讨论。在不久的将来，应该有可能制备出更高数量级的量子纠缠源，人们能够借此使用纠缠态和线性光学来实现一些量子计算算法，并利用更复杂的纠缠纯化协议和多阶段高保真隐形传送，使建设量子中继器成为可能。

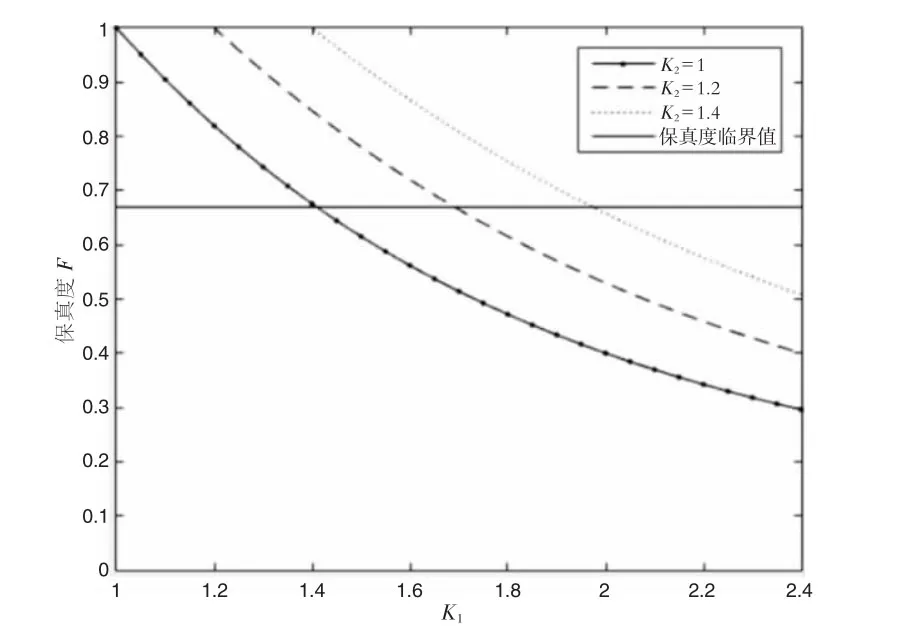
图2 保真度与信道系数比之间的关系

图中，水平实直线为保真度临界值0.6700，信道保真度从1.0000开始随着信道系数幅度比K1的增大而减小;而当K2增大时，F随K1变化的值也随之增大。当K2=1时，保真度F＞0.6700的K1临界值为K1=1.4048，即当K1＜1.4048时信道能够正确传送量子信息。同理，当K2=1.2和K2=1.4时，保真度F＞0.6700的K1临界值分别为K1=1.6887和K1=1.9790，即分别当K1＜1.6887和K1＜1.9790时信道才能够正确传送量子信息。

5 结束语

基于传统的两光子极化纠缠态的制备，给出了一种八光子纠缠态的制备方案。此方案不需要区分八个纠缠光子所处的状态，因此在实验中更容易实现，提高了制备效率。在未来随着人们所考虑光子数的不断增多，在实验上还需注意对实验参数进行控制，因此对以EPR为信道的八光子纠缠态保真度