水平和竖向地震动相干函数的比较

刘成浩



水平和竖向地震动相干函数的比较

刘成浩

苏州科技大学, 江苏 苏州 215011

为明确水平和竖向地震动相干函数之间的关系，本文选取SMART-1台阵第5次地震和第40次地震记录，采用水平分量和竖向分量加速度记录作为研究数据，用FORTRAN程序计算台站间相干系数，台站对间距选择200 m、1000 m和2000 m等3种不同的距离，分别计算得到对应的相干系数。选用Abrahamson模型对不同距离计算得到的相干系数进行拟合，比较水平和竖向分量拟合结果发现：竖向分量相干函数离散性大于水平分量。随着频率的增加，不同台站距下水平和竖向相干系数的衰减曲线均趋于一致，短距离低频率下，水平和竖向相干系数值相差较大。随着频率和台站间距的增大，水平和竖向相干系数值差距逐渐变小并趋于一致。

SMART-1台阵; 相干函数; 水平分量; 竖向分量

地震动空间变化的研究常常从地震动空间相关性的角度来描述，随着强震记录的收集，逐渐采用量化的方式来表述地震动空间相关性，常用相干函数来表示。截至目前，研究者对强震资料进行统计分析时，常根据频域功率谱的分析来求得相干函数法[1,4]。人们一般用地震动相干函数描述水平方向地震动，较少研究竖向地震动相干函数，以及比较水平分量相干函数和竖向分量相干函数的异同。在水平和竖向地震动相干性比较中，刘先明，叶继红，全伟[5-7]等发现竖向地震动相干函数和水平地震动相干函数存在差异，由此可见，地震动空间变化只考虑单一分量地震作用是不够的[8]。但是，目前少有研究对水平和竖向相干性做单独比较。本文选取台湾SMART-1台阵第5次地震和第40次地震记录，通过计算不同台站对距离下的相干系数并对所得结果拟合。分析拟合结果，比较地震动竖向和竖向之间以及水平和竖向之间的相干函数，明确水平和竖向两分量相干函数之间的关系。

1 地震动的选取及处理

1.1 地震记录的选取

本文选取SMART-1台阵[9]（见图1）第5次和第40次地震记录的水平分量和竖向分量的地震动加速度记录，第5次地震和第40次地震记录详细信息（见表1）。SMART-1台阵是一个位于冲击河谷的二维平面同心圆台阵，圆心为C00台站，半径分别为200 m、1000 m、2000 m的同心圆上各有均匀分布的13个台站。本次研究选取12个台站进行计算，其中内圈：I03、I06、I09、I12；中圈：M03、M06、M09、M12；外圈：O03、O06、O09、O12。

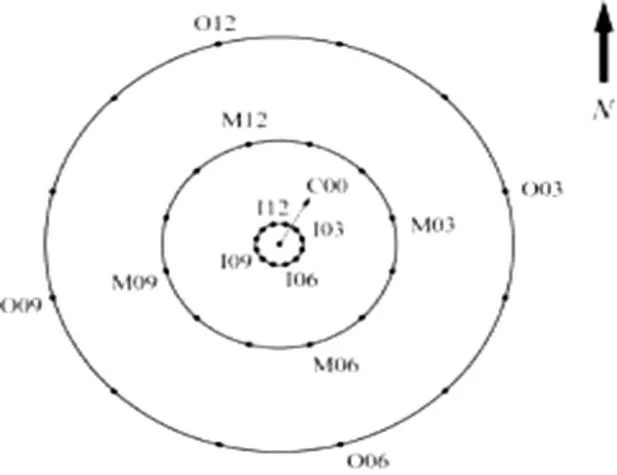
图1 SMART-1台阵布置图

表1 Event5和Event45地震动记录详细信息

1.2 数据处理

台站记录的地震波记录均为原始记录，原始数据中包含噪声、传播距离等因素的干扰，因此收集到的原始记录均需要进一步处理才能作为研究数据。本文将得到的原始加速度记录经过滤波、时移、基线校正和截取等一系列处理后，最后得到的数据作为进一步研究的数据。

2 相干函数的计算方法

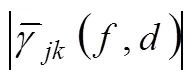
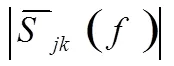
3 地震动水平和竖向相干性分析

根据台站间的位置分布特点，以C00为中心台站，分别计算C00台站与内圈、中圈和外圈台站之间的相干系数。计算台站选择：内圈取台站I03，I06，I09和I12；中圈取台站M03，M06，M09和M12；外圈取台站O03，O06，O09和O12，分别取这12个台站的地震动水平加速度分量（NS）和竖向加速度分量（V）为研究对象，计算各台站地震动分量与C00台站间的相干系数。

基于密集台站的地震记录和地震动空间相干函数的研究，学者们给出了很多经验相干函数模型和半经验相干函数模型来分析相干函数，本次研究采用Abrahamson模型对计算得到的相干系数曲线进行拟合，拟合工具选取1stOpt。

根据式（1），利用FOETRAN程序分别计算中心台站C00与内圈、中圈和外圈的相干系数，为了分析地震动竖向分量相干系数随频率和台站距离的规律，并比较其与水平分量之间的关系。将第5次地和第40次震动水平和竖向分量计算得到的相干系数，采用式（2）Abrahamson模型进行拟合（图2）。从图2可以看出，对于不同台站对距离，台站对距离越大，水平和竖向分量相干系数越小，且随着台站对距离的增大，相干系数差值越来越小。从衰减趋势来看，当频率达到一定大小时，不同台站对距离的相干系数值保持一致的衰减趋势，最终衰减趋势趋于一致。

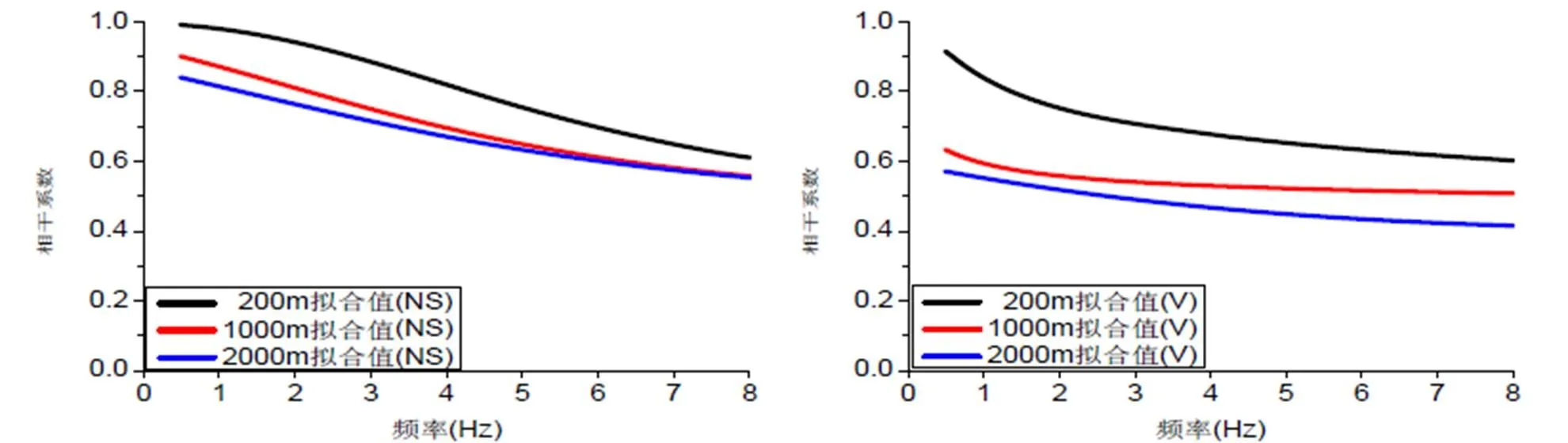
图 2 不同台站距下相干系数拟合曲线；E05

Fig.2 Fitting curves of coherence coefficient under different station distances; E05

3.1 竖向和竖向相干函数比较

比较第5次地震和第40次地震的竖向分量拟合结果（图3），图3（a）为台站距离=200 m时第40次地震和第5次地震竖向分量的拟合值比较，图3（b）和（c）分别是=1000 m和=2000 m的比较结果。第40次地震和第5次地震震级相差不大，两次地震的震源距相差较大。比较结果：第40次地震竖向分量相干函数随频率增大衰减较快，且相干函数值小于第5次地震。震源距越小，地震动竖向分量相干性越好。本次研究再次选取SMART-1台阵第33次和第40次地震进行计算，得到了相同结果。

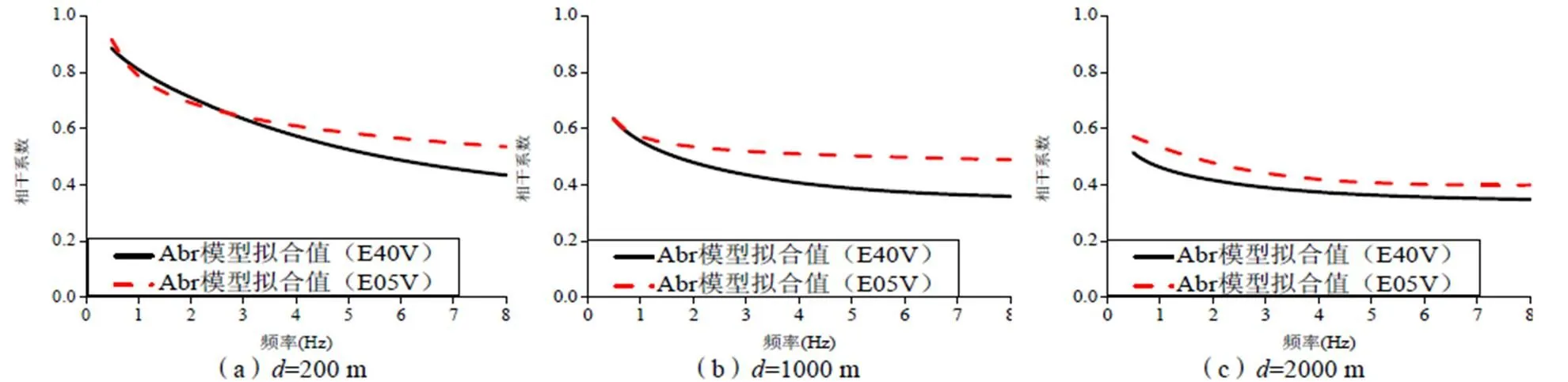
图 3 第40次和第45次地震相干系数拟合结果比较

3.2 水平和竖向相干函数比较

将第5次地震相同台站对距离下计算得到的相干系数值，然后选取Abrahamson模型，使用1stOpt拟合相干系数曲线（见图4），从图4中可以看出：竖向相干系数一开始衰减较快，随着频率的增加逐渐变缓；而水平分量相干系数一开始衰减较慢，随着频率的增加逐渐加快，竖向分量和水平分量相干系数曲线随频率的衰减趋势趋于一致。比较三种不同台站间距的拟合结果发现，台站对距离越小、频率越低，水平和竖向相干系数越容易存在差异性；台站对距离越大、频率越大，水平和竖向相干函数趋于一致。

图 4 第5次地震水平和竖向分量相干系数基于Abr模型拟合结果比较, fcut =8 Hz

为了说明水平和竖向相干系数随频率的衰减趋于一致，现另取截止频率cut=10 Hz，cut=15 Hz。计算并拟合3种台站距离下的相干系数（图5和图6），分析两者随频率的衰减趋势。

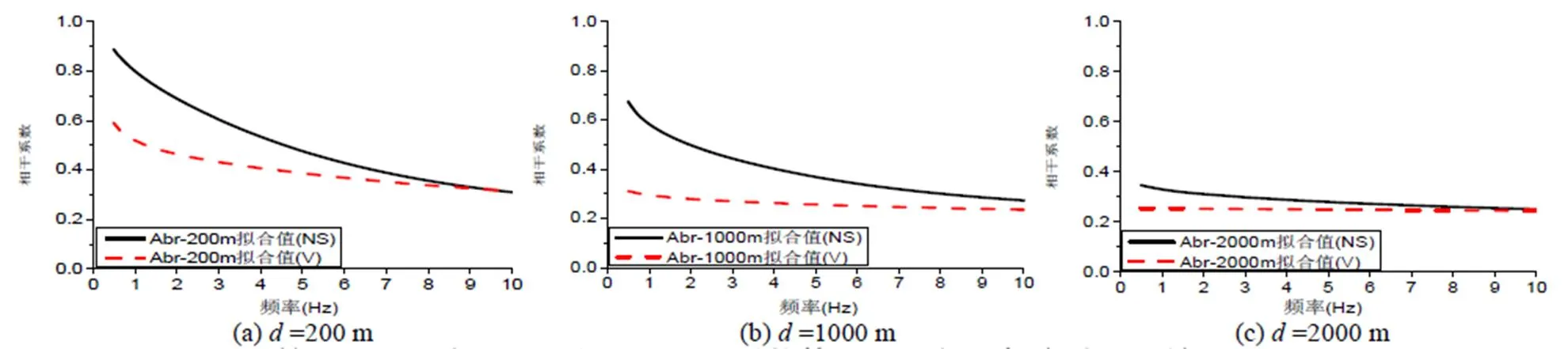
图 5 第5次地震水平和竖向分量相干系数基于Abr模型拟合结果比较, fcut =10 Hz

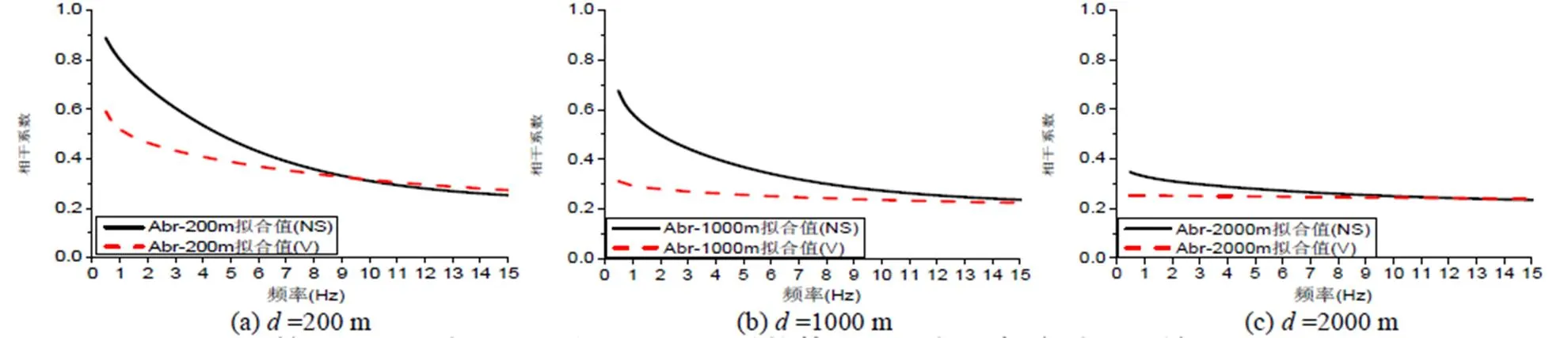
图 6 第5次地震水平和竖向分量相干系数基于Abr模型拟合结果比较, fcut =15 Hz

用同样的方法计算第40次地震，得到与第5次地震相同的结果。

4 讨论

以SMART-1台阵第5次地震和第40次地震的水平向（NS）分量和竖向（V）分量加速度记录为分析对象，计算相干系数并进行了拟合，分析比较水平和竖向地震动相干系数的拟合结果，明确了水平和竖向地震动相干函数之间的关系，为实际工程中考虑水平和竖向地震动相干性给出参考。

5 结论

（1）水平地震动相干函数离散性比竖向相干函数小，尤其是在低频处，水平相干函数离散性明显小于竖向相干函数；竖向地震动分量成分比较复杂，相干函数离散性大。

（2）震源距越小，地震动竖向分量相干性越好。

（3）短距离低频率下，水平和竖向相干系数值相差较大。随着频率的增加，不同台站距下水平和竖向相干系数的衰减曲线均趋于一致。

[1] 胡聿贤.地震工程学[M].北京:地震出版社,2006

[2] Darragh RB. Analysis of near-source waves: separation of wave types using strong motion array recordings[M]. University of California: Earthquake Engineering Research Center, College of Engineering, 1988

[3] Oldham RD. On the propagation of earthquake motion to great distances[J]. Proceedings of the royal society of london, 1900,66:2-3

[4] Oliveira CS. Variability of strong ground motion characteristics obtained in SMART-1 array[C]. Proceedings of the 12th Regional Seminar on Earthquake Engineering, 1985

[5] 刘先明,叶继红,李爱群.竖向地震动场的空间相干函数模型[J].工程力学,2004,21(2):140-144

[6] Ye JH, Pan JL, Liu XM. Vertical coherency function model of spatial ground motion[J]. Earthquake engineering and engineering vibration, 2011,10(3):403-415

[7] 全伟.大跨桥梁多维多点地震反应分析研究[D].大连:大连理工大学,2008

[8] Papazoglou AJ, Elnashai AS. Analytical and field evidence of the dam aging effect of vertical earthquake ground motion[J]. Earthquake Engineering and Structural Dynamics, 1996,25(10):1109–1137

[9] Abrahamson NA, Bolt BA, Darragh RB,. “The SMART-1 accelerograph array (1980-1987): A review”[J]. Earthquake Spectra, 1987,3:263-287

[10] 丁海平,袁莉莉,刘成浩.窗函数和带宽对地震动相干函数的影响[J].自然灾害学报,2018,27(3):1-10

Comparison of Coherence Functions in Horizontal and Vertical Ground Motion

LIU Cheng-hao

215011,

In order to clarify the relationship between horizontal and vertical ground motion coherence functions, this paper selects the 5th and 40th seismic records of SMART-1 array, and uses horizontal component and vertical component acceleration records as research data, and calculates with FORTRAN program. For the coherence coefficient between stations, the station selects three different distances, such as 200 m, 1000 m and 2000 m for the spacing, and calculates the corresponding coherence coefficients. The Abrahamson model is used to fit the coherence coefficients calculated by different distances d. The horizontal and vertical component fitting results are compared. It is found that the vertical component coherence function is more discrete than the horizontal component. With the increase of frequency, the attenuation curves of the horizontal and vertical coherence coefficients of different stations tend to be the same. At short distances and low frequencies, the horizontal and vertical coherence coefficients differ greatly. As the frequency and station spacing increase, the gap between the horizontal and vertical coherence coefficients becomes smaller and tends to be consistent.

SMART-1 array; coherence function; horizontal component; vertical component

P315.9

A

1000-2324(2019)02-0251-04

10.3969/j.issn.1000-2324.2019.02.017

2018-02-12

2018-05-23

刘成浩(1994-),男,硕士研究生,主要从事地震工程研究. E-mail:chaunceyliu@yeah.net