基于灰色模型的连续累计自动衡器测量不确定度评定
2019-05-07李冰莹李永新马宇明董祥辰
李冰莹,李永新,马宇明,董祥辰
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.江苏省计量科学研究院,江苏 南京 210023)
连续累计自动衡器发展至今己有上百年,使用范围在不断扩大、使用领域也越来越宽,现广泛应用于交通运输、矿山开采、能源发电、冶金建材、粮油加工、国内外贸易、能源计量、节能减排等众多领域。但在实际使用中,随着被称重物料的流量、皮带速度、运行时间、环境条件等多个影响因素的变化,称重精度下降很快,带来的动态计量失准问题也越来越突出,大多数产品只能达到±5%的精度[1]。计量性能失准,导致对大宗物料进行贸易结算时失去公正,使能源计量和节能减排失去准绳和基础。为此,很有必要研究连续累计自动衡器的测量不确定度,以科学评定连续累计自动衡器称重结果的计量准确度,争取使连续累计自动衡器市场产品都能满足其出厂标称的计量性能参数指标,满足使用要求。
1 测量不确定度
测量不确定度理论从被测量值的分散性角度,用“测量不确定度”描述测量结果的优劣,关注被测对象自身测得值的可能分布,方便测量结果的使用[2]。其中,由“测量系统(仪器)”引起的分量,即所谓“测量系统(仪器)的测量不确定度”,通常是测量结果不确定度的重要组成分量。
按照目前国际上通行的测量不确定度评定原则,多数是采用基于纯粹统计方法的测量不确定度评定办法计算得到测量系统或仪器的测量结果不确定度uε,主要是通过大量的校准实验,对所获得的“测量误差”ε之测得值序列进行统计分析和加工处理,以标准差表征测量结果的离散程度。其结果的可靠程度不仅与重复性条件下测量的次数有关,同时还与测量结果的概率分布函数有关,前提是基于大样本量和典型概率分布[3-4]]。
现在行业内普遍评定方法是将连续累计自动衡器测量误差近似为正态分布,利用贝塞尔公式求解标准不确定度。实际连续累计自动衡器称重过程中,受到外界环境条件和自身内部结构改变的影响,计量特性随着时间不断变化,具有时变性的特点,这一特点必然在测量误差中体现,使测量误差中包含许多所谓的“非平稳的随机量”,相应有限序列的“标准差”也会具有时变的特性,若照用此不稳定的“标准差”表征所关注的测量不确定度,将会带来较大偏差。
2 连续累计自动衡器灰色评定模型
经典灰色系统理论的观点是:一切客观系统,即使表象繁杂,表征数据分散,但它总是具备整体功能,总是有顺序的,系统内部因素存在着必然联系,蕴含着内在规律,各因素综合起来表现出系统的整体功能性。灰色系统理论的优点是对样本量没有标准要求,同时对概率分布也没要求。近年来,该方法广泛应用于对已知信息少、样本小、具有不确定性的系统进行未知信息的预测,使系统由“灰”色变为“白”色[5-7]。
给测量系统带来不确定性的影响因素形态百异,有动态的、有随机性的、有系统性的,形成也许是“非平稳”的随机变量,而灰色系统理论把一切随机变量都当作是在一定取值范围内变化的“灰”量。所以,可将测量系统自身不确定变化过程当作一个灰色过程,应用灰色系统理论进行不确定变化规律的建模[7]。
连续累计自动衡器测量系统的信息量是时变的,影响量是不确定的,将一段时期内不同时间点得到的物料称重结果视为一组动态变化的数据序列,该数据序列不仅表现出时变性和相关性,而且数据结构形式复杂,很难做到用确定的数学公式来表述。系统具有“外延明确,内涵不明确”的特征,即灰性,可以将连续累计自动衡器称重序列看作灰色过程。
连续累计自动衡器动态物料称重结果,是通过持续测量称重托辊上表示单位输送带长度上的载荷值q(kg/m),与相同时刻皮带的速度测量值V(m/s)相乘后对时间积分得到,即影响称重结果的有q和V两个主要变量,且q和V之间无动态关系。因此,选择建立称重系统的灰色模型(grey model)GM(0,2)序列,GM(0,2)的建模基础是原始数据的累加生成值。
假设对同一物料的一组重复称重数据序列X=[x(k)|k=1,2,3,…,n],用称重次数k作为横坐标、用测得值作为纵坐标画图,如图1。

图1 原始称重数据序列示意Figure 1 Schematic diagram of the original weighing data sequence
对一个理想的称重计量过程,如果不存在测量误差,那么每次称重结果都可看作是被测物料的真值,如图1中直线1示意;而实际称重计量过程中,因为存在多种不确定因素,导致每次称重结果可能接近但又不等于被测量的真值,却又分散分布在真值周围,如图1中的曲线2示意。
将数据序列X按从小到大排列成序列X(0),有
X(0)=[x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)]。
(1)
将序列X(0)累加后生成一新序列X(1)有
X(1)=[x(0)(1),x(0)(1)+x(0)(2),x(0)(1)+x(0)(2)+x(0)(3),…,x(0)(1)+x(0)(2)+x(0)(3)+…+x(0)(n)]。
(2)
用称重次数k作为横坐标、用累加测得值作为纵坐标画图,如图2。

图2 累加称重数据序列示意Figure 2 Schematic diagram of the cumulative weighing data sequence
图2中的直线1和曲线2的位置关系只是示意,根据实际称重数据,有各种可能位置布局,直线1表示理想无测量误差的称重过程,曲线2表示实际有测量误差的称重过程。正是因为存在着测量误差,导致累加生成得到的测量序列,由理想的线性关系转变成近似指数规律。直线1和曲线2在横坐标取定、沿纵坐标方向的差值可反映出称重误差的大小,二者差值经过一定公式转换也可反映代表称重结果的数据样本的离散性,从而反映称重结果的测量不确定度[8]。令
(3)
Δmax=max[Δ(1),Δ(2),Δ(3),…,Δ(n)]。
(4)
Δ(k)描述了单次物料称重试验的测量值与物料真值之间的差值,当测量值与真值之间的偏差越大,那么在该点代表累加测量值的曲线2和代表累加真值的直线1之间偏离程度就越大,曲线2就更远离直线1也更陡峭。这也从侧面说明当代表累加测量值的曲线弧度越大,则称重结果变化越大,多次称重结果围绕被测物料真值的离散程度也越大[9]。所以称重数据的离散程度可通过Δ(k)这个参数来表征。
定义标准不确定度u的灰色评定模型为
u=cΔmax/n。
(5)
式(5)中,c为灰色常系数,n为称重次数,c的大小求取过程:由计算机产生n个符合某一分布的随机数集;依次对集合中前m(m=1,2,…n)个数计算其标准差;对计算得到的标准差生成一次累加序列;再基于灰色模型GM(0,2)参数的最小二乘法表达式,利用软件仿真得到c值。当测量数据的概率分布不明确或者样本较小时,采用公式(5)表示的测量结果标准不确定度的灰色评定模型,通过大量仿真和实例应用得到的评定结果均具有较高可靠性[9]。即使测量数据分布差异很大,但c变化很小,若数据为正态分布时,c仿真结果为2.5;数据为瑞利分布时,c仿真结果为2.41;数据为均匀分布时,c仿真结果为2.35,也侧面说明灰色评定模型对测量数据分布的依赖性较小[10]。
3 算例分析
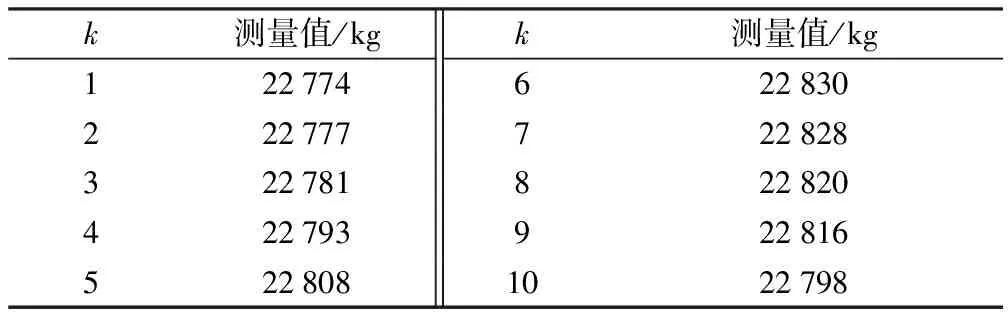
现有一台连续累计自动衡器,对累计载荷质量为22 800 kg的物料进行测量,10次称重数据如表1。
表1 连续累计自动衡器1所得称重测量序列
Table 1 Weighing measurement sequence of continuous totalizing automatic weighing instrument 1
k测量值/kgk测量值/kg1227746228302227777228283227818228204227939228165228081022798
使用Lilliefors检验,得到此组数据被接受为正态分布的概率为77.5%,可认为此组数据分布与正态分布较接近。根据式(1)~(5)计算标准不确定度u2≈22 kg。如使用传统贝塞尔公式计算得到标准不确定度s2≈21 kg。可见,利用灰色模型评定与传统方法评定的标准不确定度非常接近,这从侧面反映了灰色模型评定标准不确定度的有效性和适用性。
使用另一台连续累计自动衡器,对累计载荷质量为22 800 kg的物料进行测量,10次称重数据如表2。
表2 连续累计自动衡器2所得称重测量序列
Table 2 Weighing measurement sequence of continuous totalizing automatic weighing instrument 2

k测量值/kgk测量值/kg1228176228212228107228093227948227934228069228215228201022822
使用Lilliefors检验,得到此组数据被接受为正态分布的概率为31.3%,可认为此组数据分布与正态分布相差较大。根据式(1)~(5)计算标准不确定度u1≈6 kg。如使用传统贝塞尔公式计算得到标准不确定度s1≈11 kg,采用灰色模型评定得到的标准不确定度比传统方法评定结果缩小近一倍。二者相差较大的主要原因是采用贝塞尔公式计算标准不确定度的传统评定方法为了安全起见,默认所有称重数据均为正态分布,当实际数据分布与正态分布相差较大时,导致标准不确定度计算结果偏大,可见,当称重数据分布与正态分布相差较大时,灰色评定模型更能真实反映连续累计自动衡器称重结果的计量准确性。
利用灰色模型GM(0,2)求得称重结果的标准不确定度后,参照现行《不确定度指南》中规定方法,通过合成由标准器、分辨力等引入的不确定度分量,可求得合成标准不确定度,如需进一步求取扩展不确定度,再将合成标准不确定度乘以选定的扩展因子即可。
由于连续累计自动衡器称重原理、结构形式、使用环境、所载物料等都不尽相同,影响其称重结果精度的因素不同,导致测量结果的分布不同。且连续累计自动衡器试验运行经济成本高昂,单次测量准备工作较耗时,想在同一时期短时间内取得大样本容量、确定称重序列的概率分布难度较大,传统评定方法的适用性有待进一步考证,而灰色模型由于对测量结果分布没有太多要求,故在连续累计自动衡器不确定度评定中适用性更强。
4 结 语
灰色评定模型对测量数据样本容量及其分布没有要求,在大样本容量及典型概率分布时与传统统计评定方法计算的结果接近;在小样本容量及分布不明确时,灰色评定模型较传统统计评定结果更接近于理论值。恰好符合连续累计自动衡器实际称重结果样本容量小、分布不明确的特点,且建模方法简单、计算量小,不失为对现有连续累计自动衡器不确定度评定方法的一个有益补充。
