数据预处理对BP神经网络拟合铁氧体导热系数的影响
2019-05-07郑燕鹏王晓娜侯德鑫叶树亮
郑燕鹏,王晓娜,侯德鑫,叶树亮
(中国计量大学 计量测试工程学院 工业与商贸计量技术研究所,浙江 杭州 310018)
导热系数的有效测量是研究其导热性能、评价材料表面状况的重要内容之一。测量铁氧体的导热系数实质上是一个求解导热反问题的过程,其导热系数是一个随铁氧体物理特性变化的非线性函数。常用的导热系数测量方法分为稳态法和非稳态法两大类[1]。但是稳态法比较原始、测定时间较长和对环境要求苛刻。非稳态测量法多用于研究高导热系数材料,或在高温条件下进行测量[1]。
BP神经网络具有强大的非线性映射、自组织、泛化、误差反馈调整和容错能力[2],被广泛应用于模式识别、拟合及预测领域。Sablani等人[3-4]利用神经网络方法建立了食品导热系数的预测模型,得到了导热系数随含水率、温度和表观孔隙率的变化规律。徐旭[5]等利用神经网络建立起木材的温度和孔隙率与导热系数之间的映射模型。刘帅[6]等利用BP神经网络建立了毛竹的温度和密度与导热系数之间的映射模型。从导热性能上看,铁氧体与食品、木材、毛竹等都属于低导热材料,有一定借鉴意义。参照上述文献中的BP神经网络,应用到铁氧体导热系数拟合中,发现预测相对误差较大。在实际使用中,标准BP神经网络处理大批量数据时训练速度慢、容易收敛于局部最小点等缺点,导致训练的BP神经网络模型具有较强的随机性和不确定性,使用效果受到影响。针对这些问题,国内外进行了大量研究,多数集中于BP算法的改进、权值阈值初始化等方面,也取得了大量的成果[7-9]。针对数据预处理方面的研究较少,常见的数据预处理方法有归一化、中心化、标准化等[10]。张昊采用三种数据归一化方法,分析基于BP神经网络的GPS高程拟合建模中样本数据预处理的必要性,并对比了几种数据预处理方法的优劣[10]。朱庆生提出通过线性运算将样本数据的各个字段值统一到同一个数量级,然后结合数值归一化的方法。在基于信令的漫游用户实时信用度测评及欠费风险超前控制系统中,使用该方法预处理样本数据取得了很好的预测效果[11]。
本文针对传统BP神经网络在铁氧体导热系数拟合计算时,低导热系数数据预测相对误差较大的问题,分析其原因,提出对目标输出进行非线性化处理再归一化的数据预处理方法,结合最大相对误差与平均相对误差的评价方法,验证了该方法的有效性。
1 改进数据预处理方法的必要性
利用常规BP神经网络对铁氧体导热系数进行非线性映射。实验软件为MATLAB R2016b,输入数据为50帧温升数据,如图1,目标输出为铁氧体对应的导热系数。样本共有10 000组,随机取8 000组作为训练数据集,2 000组为测试集。该神经网络输入节点数设为50,输出层节点为1,隐含层节点数采用公式(1)计算:
(1)
式(1)中,h为隐含层神经元个数,m为输入层神经元个数,n为输出层神经元个数,a为变量,取值范围为1~10。这里取个数为10~18共9种情况。采用tansig激活函数和最小均方误差训练算法。训练终止条件:目标均方误差0.000 01、1 000次迭代、误差梯度连续上升7次,以相对误差函数Ek来评价神经网络:
(2)
式(2)中,Ek为相对误差,λp为神经网络预测得到的导热系数,λo为目标输出值。
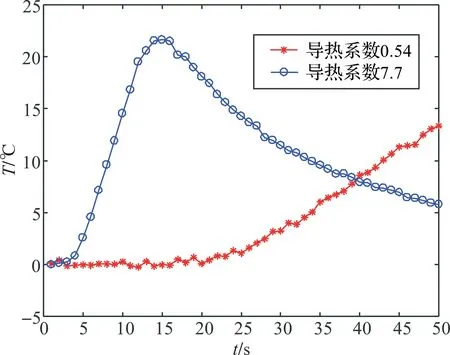
图1 输入数据温升图Figure 1 Temperature-rising chart of input data
图1中,星号线是导热系数为0.54的样品在50帧中的温升数据,圆圈线是导热系数为7.7的样品在50帧中的温升数据.从图可知,不同导热系数的样品在相同激励条件下温升曲线不同。
输入数据和目标输出采用式(3)进行归一化,然后输入至BP神经网络进行训练:
(3)
对得到的模型进行测试,发现每一次训练得到的模型预测结果均不相同,如图2。图2(a)的最大相对误差达到32%,而图2(b)中的最大相对误差约为40%。

图2 权值随机初始化模型相对误差Figure 2 Relative errors of models after initializing weights randomly
查阅文献[7-9]可知,BP神经网络每次训练时,权值和阈值都是随机赋值的,而且BP算法容易陷入局部最优点而非全局最小点,从而导致每次训练结果不一致。为减少偶尔因素的影响,每种工况下用相同的数据随机初始化训练30次.对评价方法进行改进,采取3种指标对神经网络进行评价,最大相对误差Emax、每种导热系数数据平均相对误差Er,如式(4),和整个数据集上的平均相对误差Ea,如式(5)。
(4)
(5)
式(4)中,N为训练次数30次,Er为平均相对误差,λp为神经网络预测得到的导热系数,λo为目标输出值。式(5)中num为测试集数据个数,其他参数与式(4)中一致。
以改进的评价方法对网络进行评价,得到图3所示结果。

图3 平均相对误差Figure 3 Average relative errors
对图3进行统计分析,近95%的数据平均相对误差Er低于5%,近1%的数据在导热系数低于2的情况下,平均相对误差Er超过10%,最大达到30%~40%。4%的数据的平均相对误差Er在5%与10%之间,整个网络在测试集数据上平均相对误差Ea为4.57%。因此,本文研究如何降低低导热系数(低于2)数据的相对误差,最直接的做法是进行分段训练;即导热系数低于某个值的数据进行训练,得到低导热系数拟合模型,导热系数高于某个值的数据进行训练,得到高热系数拟合模型。以导热系数6.5作为分界线为例,最大相对误差能够从30%~40%降低到20%~25%,如图4。

图4 低导热系数数据训练模型相对误差Figure 4 Relative errors of models after training low thermal conductivity data
对比图4和图3可知,采用分段训练方法,能降低低导热系数数据最大相对误差。但是,降低效果不佳,而且实际使用时不知被测铁氧体的导热系数,无法选择低导热系数模型还是高导热系数模型进行拟合。因此,需要采取更有效的措施来解决低导热系数数据相对误差较大的问题。
2 数据预处理改进方法
2.1 数据预处理方法选择
通常,在做时序预测时,输入数据的数值范围将存在一定差异,当差异达到数量级时,网络在学习时受到各种特征的影响不一,权值偏重于数值较大的特征,就可能学习不到数值较小的特征,或者网络学习速度变慢甚至不能收敛[11]。第二章实验表明,目标输出差距过大会影响网络性能。导热系数的定义式[12]如式(6):
(6)
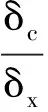
本文输入数据是用热像仪观测到的热序列,其与导热系数λ呈正相关性。由于数据是在相同条件下获得的,忽略随机误差,则低导热系数数据中的绝对误差与高导热系数中的绝对误差相同。导热系数低,热像仪记录的温升也低,与高导热系数相比,其相对误差就较大。温升效果曲线见图1。常规线性化处理方法只是等比例放缩,对此问题无效。基于此,提出一种非线性数据处理方法对导热系数进行处理,以减小低导热系数数据与高导热系数数据之间的相对误差。
适合本问题的非线性函数有三种:
1)对数函数.这里取自然对数,其公式为
y=lnx;
(7)
2)反正切函数.反正切函数公式为
y=arctanx;
(8)
3)Sigmoid函数.Sigmoid函数公式为
(9)
要使得低导热系数数据和高导热系数数据之间的相对误差最小,则需要非线性函数能最快地将两个值减小,也就是该函数的斜率要大。分别对三种函数进行求导,得式(10)、(11)、(12),x的定义域为[0.5,10],在相同输入下,式(10)的值最大,对数函数的斜率最大,所以本文选择对数函数为非线性处理函数。
(10)
(11)
(12)
2.2 数据预处理方法步骤
在训练神经网络之前,对输入数据采用公式(5)进行归一化,对目标输出采用公式(7)进行非线性处理并归一化,在预测输出时,先反归一化再按照公式(13)进行反运算即对网络原始预测输出值进行指数换算,便可得到与目标输出对应的预测输出:
(13)

3 实验验证
实验时,在传统神经网络基础上,采用改进后的数据预处理方式进行实验。分别分析了隐含层神经元节点个数和隐含层个数的影响,并与相同工况下、相同样本、传统数据预处理方式的网络进行对比。从测试集上平均相对误差预测图上看,单、双隐层下,不同神经元的预测图大致相同。这里在单隐层双隐层、目标输出非线性处理和未非线性处理的条件下各取一组图进行说明不同导热系数相对误差分布信息,以及低导热系数情况下,最大相对误差信息如图5。

图5 不同数据预处理方法相对误差对比图Figure 5 A comparison diagram of relative errors after adopting different data preprocessing methods
由图5可知,经过非线性处理后的数据训练得到的BP神经网络其网络预测精度要高于未经过非线性处理训练得到的BP神经网络。整个数据集上,大部分数据平均相对误差要明显减小,最大相对误差也有明显减小。进一步进行定量分析,图6中列举了改进数据预处理和传统数据预处理训练得到的网络测试集平均相对误差Ea在不同工况下变化图。表1列举了在不同工况下,改进数据预处理和传统数据预处理训练得到的网络在测试集数据上,最大平均相对误差和平均相对误差超过10%的数据个数。

图6 测试集平均相对误差Ea随工况变化图Figure 6 Variation diagram of average relative errors Ea of test sets with working conditions
Table 1 Errors of test datasets under different working conditions

网络架构最大平均相对误差Emax/%Er超过10%的个数(数据集占比%)单隐层非线性处理12~142(0.1)单隐层未非线性处理25~358-10(0.4~0.5)双隐层非线性处理12~142(0.1)双隐层未非线性处理18~206~8(0.3~0.4)
从图6和表1可知,改变隐含层节点数,不能提升神经网络预测准确度。在单隐含层情况下,采取导热系数非线性变换的实验组比不进行该处理的实验组网络预测精度大约有35%的提升,最大平均相对误差从25%~35%降低到了12%~14%,平均相对误差从4.8%降到了3.1%,平均相对误差超过10%的数据个数由8~10减少到了2个。在双隐含层情况下,采取导热系数非线性变换的实验组比不进行该处理的实验组网络预测精度大约有25%的提升,最大平均相对误差从18%~20%降低到了12%~14%,平均相对误差从3.8%降到了3.1%,平均相对误差超过10%的数据个数由8~10减少到了2个。在不进行导热系数非线性处理的情况下,双隐含层的网络性能要比单隐含层的网络性能大约有20%的提升,平均相对误差从4.8%降低到3.8%。
4 结 论
针对BP神经网络拟合铁氧体导热系数,低导热系数数据预测相对误差较大的问题,提出对目标输出进行对数运算后再归一化的数据预处理方法.并将该方法与常规数据归一化方法进行对比分析,结论如下。
1)在单隐含层时,采用非线性处理后得到的模型比常规归一化得到的模型预测精度有大约35%的提升。
2)在双隐含层时,采用非线性处理后得到的模型比常规归一化得到的模型预测精度有大约25%的提升。
采用非线性处理后得到的模型在测试集数上平均相对误差最优能达到3%,采用非线性处理方法能有效降低低导热系数数据预测相对误差。本文提到的思路对于解决神经网络中数据集中数据差异较大的问题,具有一定的借鉴意义。
