基于PSCAD配电网合环电流仿真与分析∗
2019-05-07邵文权张志华
周 宁 邵文权 张志华 姚 迪
(1.西安工程大学电子信息学院 西安 710048)(2.国网陕西省电力公司电力科学研究院 西安 710100)
1 引言
我国配电网通常采用“闭环设计,开环运行”的供电方式[1]。一般情况下,为确保配网的辐射状运行结构,合环开关为关断状态。当配电网某个母线、开关发生故障或者线路、设备检修时,通过闭合联络开关进行负荷转移,可以减少用户停电时间,保证电网安全稳定运行[2]。但在合环操作时,联络开关两端会产生较大的冲击电流,稳定后电网中会存在较大环流,这会导致相连的母线或馈线上的继电保护误动作[3],从而造成大面积停电。因此,对合环电流进行准确的计算分析,模拟现场的合环操作,找到最佳合环路径,对于减少停电损失,提高供电可靠性具有很重要的实际意义。
文献[4]对合环冲击电流建立了频域模型,但拉普拉斯反变化的计算较为繁杂,实际效率不太高,而且文中没有对冲击电流的有效值进行推导;文献[5]对合环系统建立了等值模型,分析了影响合环操作的主要因素,并提出了对应的解决方法,但模型过于理想化,计算结果与实际偏差较大。文献[6]在简化的网络模型上得出了合环稳态电流和冲击电流的数学表达式,但对影响合环电流较大的馈线负荷位置没有详细分析。本文利用PSCAD软件对不同合环类型下各条10kV馈线的合环操作建立仿真模型,通过对影响合环电流的主要因素进行仿真分析,给出合环判断,找到最佳合环路径。
2 配电网合环简介
配电网典型结构如图1所示,当10kV母线停电检修或其馈线出现故障时,就需要闭合联络开关,将一侧的负荷转移到另一侧馈线上,保证配网不间断供电,这种通过合环开关来联络两端馈线的操作就称为合环操作。
如图1所示,配电网合环操作大体可分为以下三种模式。
1)同一变电站来自不同区域的10kV馈线之间的合环,例如合环操作1,母线A,B都属于变电站A,但其上级电源来自不同分区,实际情况大多都是这种。
2)上级110kV电源相同,经同一变电站内不同主变低压侧10kV馈线或母线之间的合环[7]。当高压电网出现故障时,可以通过母线联络开关进行合环操作,比如合环操作2。这类合环操作冲击较小,相对更安全。

图1 配电网合环操作模式
3)同一电压等级不同变电站之间的10kV馈线合环,合环操作3属于这种情况。由于变电站不同和其带有较大差异的负荷,这种合环操作会产生较大的冲击使环网存在较大风险。
合环操作1和3的联络开关两端电压差的影响因素较多,不仅包括上级电网运行方式的影响,而且还包含上级变电站变压器容量、短路阻抗、合环馈线的阻抗以及变压器变比等因素的影响[8]。因此,这两种情况下合环开关两端电压差异可能会比较大,合环操作风险较高。
合环操作2的合环馈线来自同一变电站,合环开关两侧电压差总体受馈线阻抗与负荷分布差异的影响。在母线联络或者负荷分布较均匀,线路参数也变化不大的情况下,联络开关两侧电压向量差异较小,而且两端负荷接近时合环风险相对较小。
3 配电网合环电流数学模型
3.1 合环电流产生的原因
合环操作时产生环流的原因主要有两个:当合环点两侧a、b处于不同变电站或者同一变电站但主变容量不同时,由于所带负荷不同,两端母线电压幅值和相角均有所偏差,使得合环瞬间产生较大的冲击电流,造成合环电流变大;联络开关两侧10kV母线对系统的短路阻抗不同也会产生环流[9],影响电网安全稳定运行。
3.2 合环电流的计算模型
合环电流的计算包括合环瞬间冲击电流和循环电流的计算,对合环电流准确地计算可以有效防止电流越限对设备造成过载或继电保护误动作。下面分别建立稳态环流和合环冲击电流的数学模型。
3.2.1 循环电流计算模型
由叠加定理可知,合环后馈线首端稳态电流由合环前的馈线首端电流与环流叠加而成[10]。定义İ与 İ′为合环前、后馈线首端电流,İc为联络开关两侧电压差引起的稳态环流,则合环后馈线稳态电流可表示为

其中合环前的馈线电流İ可通过调度SCADA系统得到,而循环电流İc则可以通过合环点两侧电压的矢量差除以合环回路的总阻抗得到。即循环电流的计算公式为

3.2.2 冲击电流计算模型
鉴于电力系统三相对称,故以A相为例分析合环瞬时冲击电流。如图2所示,用a,b两点表示联络开关两端的节点,根据戴维南等效定理,从a,b两节点向环网内看,可以形成合环冲击电流的等值电路[11]。

图2 简化的合环冲击电流等值电路图
由于整个电路呈感性,合环过程从暂态到稳态是振荡衰减的[12],合环电路的冲击电流可以通过建立时域微分方程来求解,即:

Em是等值电势U̇oc的幅值,α为合环操作t=0时刻U̇oc的初始相角,它是由合环点两侧电压相角差决定的,it为t时刻合环电流瞬时值。
解微分方程(3)分别得到非齐次微分方程的通解和特解,方程的通解为合环电流的非周期分量:

将式(7)中的 α 改为 α-120°和 α+120°即可得到B相与C相的冲击电流表达式。一般而言,冲击电流受电压相角差较幅值差的影响更甚,因此研究电压相角差更有利于减小合环冲击。比如当α-φ=kπ,k=0,1,2…,直流分量为零,合环电路即时进入稳态;当α-φ=π 2,直流分量初始值与交流分量幅值相等,此时冲击电流达到最大值。
因此在合环后半个周期出现最大瞬时冲击电流iM,此时:
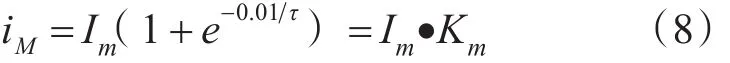
式中τ=L R,由等值阻抗的电阻和电抗决定,其中Km=1+e-0.01τ是冲击系数。对于具体的配网环路,最大冲击电流值等于稳态环流乘以一个固定的冲击系数Km。
一般情况下,合环瞬时冲击电流具有幅值高持续时间短的特点。由其特点可知,冲击电流容易引起电流速断保护动作,而速断保护的电流根据有效值整定。所以考虑采用在以时刻t为中心的一个周期内瞬时电流的方均根值求得冲击电流有效值[13]。为了简化计算,假定合环电流的周期分量和非周期分量在一个周期t里保持不变,则合环冲击电流有效值可表示为
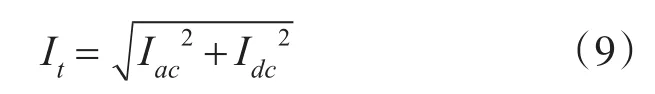
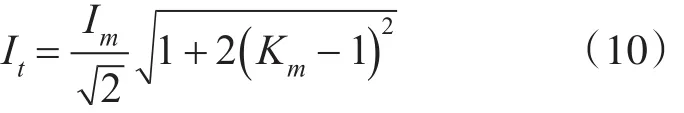
从上述推导过程可得:影响合环电流的主要因素为合环开关两侧电压差(包括幅值差与相角差)和环网总阻抗。合环电流的大小与合环点两侧电压差成正比,与环网总阻抗成反比[14]。而对于一个具体的环网其等值阻抗基本不变,因此,为了提高合环成功率,应调整运行方式以减小合环点电压的向量差找到最佳合环路径。
4 算例分析
4.1 配电网合环仿真建模
本文对该地区三种合环模式下各馈线合环建模,对合环冲击电流的暂态过程进行仿真分析。以合环模式1为例进行详细说明,其余两种模式类似。仿真图如3所示,设定220kV母线为无穷大系统,即作为系统的等效电源点。220kV及以上系统用电压源等效,并设定其相角为零。输电线路使用电缆和架空的混合线路。实际变压器采用PSCAD软件自带的双绕组变压器等效,10kV母线上的非合环馈线负荷则用恒功率负荷模型,并采用与实际计算最为接近的负荷后置方式[15]。合环两端采用集 中 负 荷 分 别 为 S左=22.91MVA ,S右=13.56MVA,功率因数为cosφ=0.9,线路参数见表1。
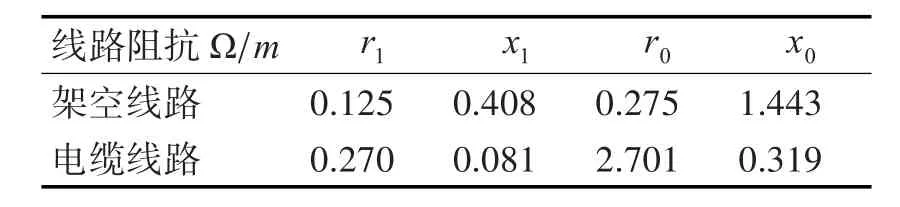
表1 典型环路的线路参数

图3 合环仿真模型
4.2 分析结果
假设合环时刻为0.2s,设置仿真时长为0.5s。i1和i2分别表示合环两端馈线首端电流,i3是通过联络开关的电流。分别提取合环前后i1、i2和i3的电流波形,如图4~6所示。图7为合环前后两侧电压相角差的变化曲线。
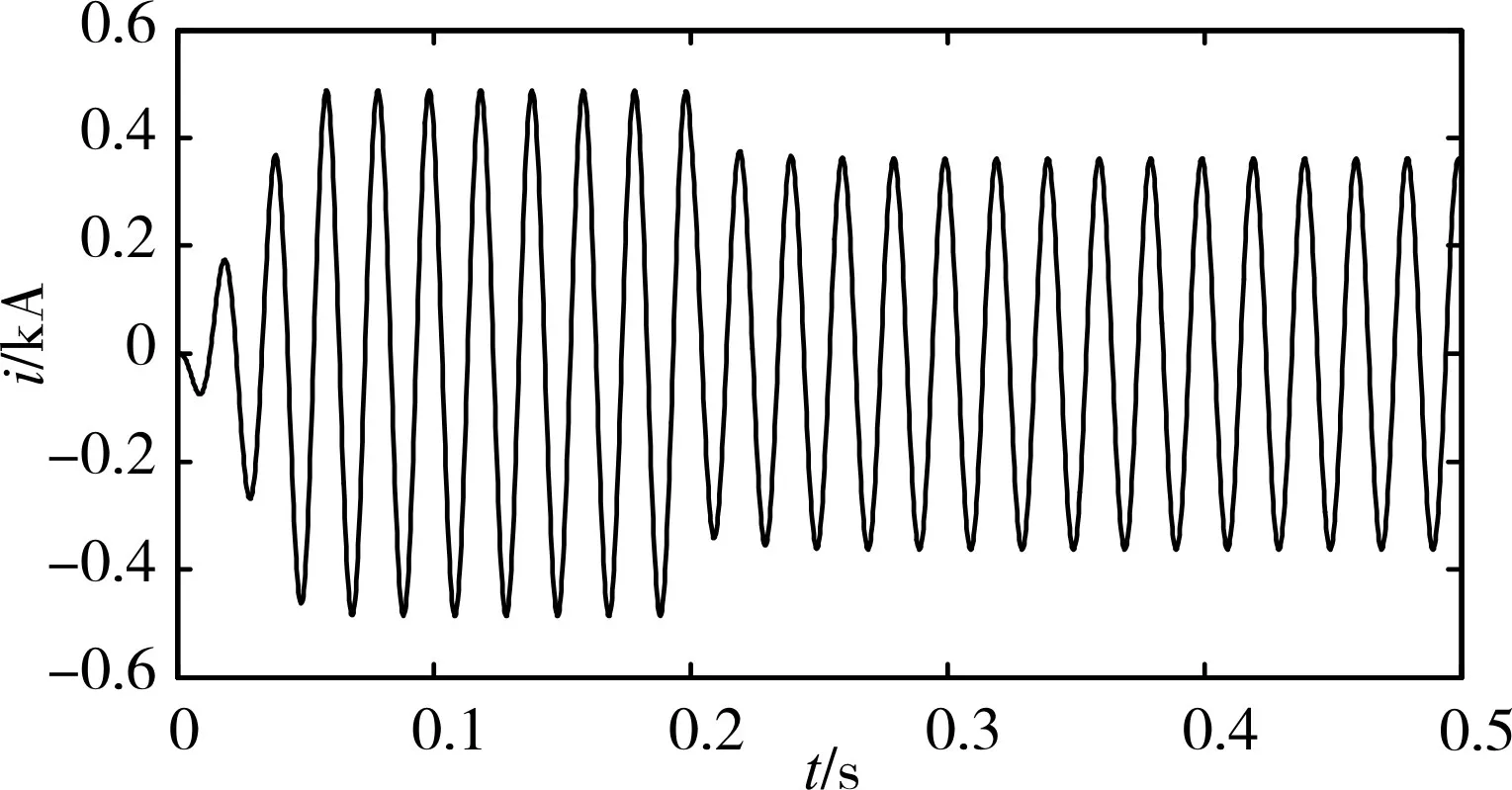
图4 合环前后i1电流曲线
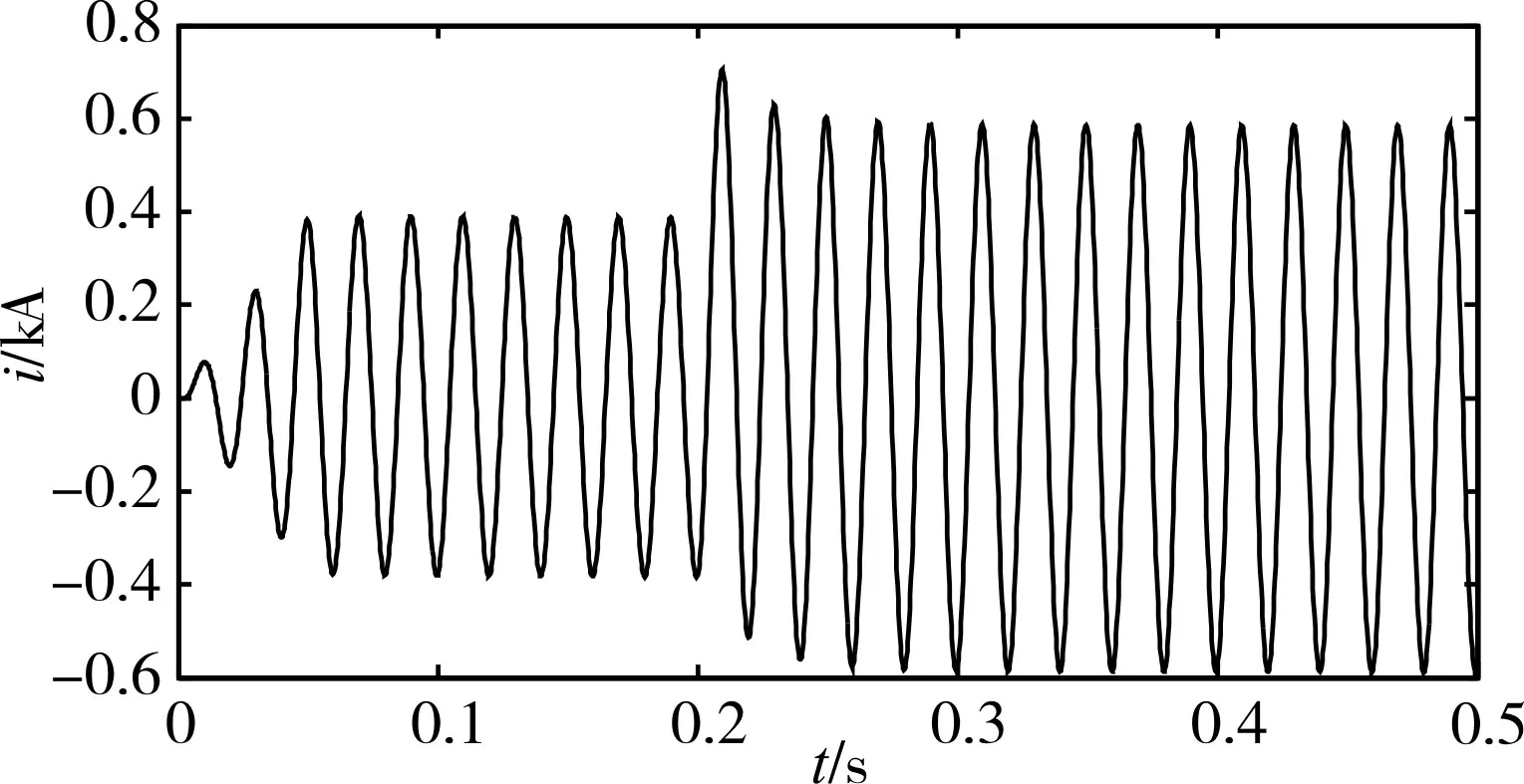
图5 合环前后i2电流曲线
由图6可知,前0.2s联络开关断开电流值为零,0.2s后闭合联络开关电流发生突变,合环冲击电流峰值出现在0.21s附近,为了寻求更有利的合环条件,分别对三种合环模式进行仿真分析,对比各项数据结果如表2所示。表中ΔU、Δδ分别表示联络开关两侧电压幅值差、相角差;iM为流过联络开关的冲击电流;I′表示合环后右馈线首端稳态电流;I′M表示右馈线首端冲击电流。

图6 合环前后i3电流曲线

图7 合环前后相角差曲线
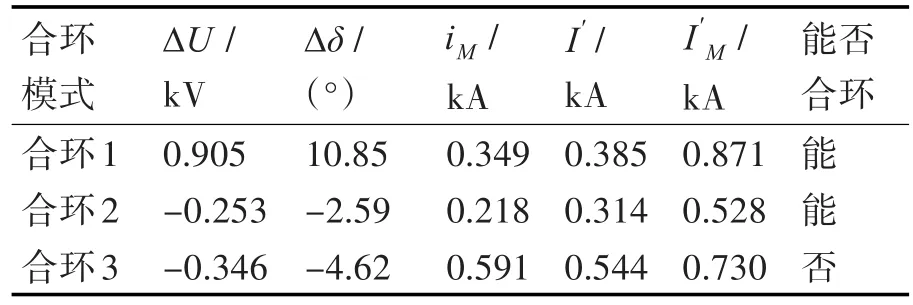
表2 三种合环模式下各合环因素对比
根据表2可知,合环稳态环流、冲击电流主要与合环点两侧的电压幅值差和相角差有关。合环模式2较之其他两种有更小的电压幅值差和相角差,由此给线路带来的冲击最小,更容易合环成功。
然而在实际合环操作中,往往有多个不同负荷(非集中负荷),而不同负荷之间的合环操作对合环电流影响较大。因此在上述合环条件最有利的模式2下将合环点左侧负荷按照实际情况分成三条不同的馈线负荷,取右侧集中负荷为S右/2=6.10+j2.90。分别仿真分析以寻找最佳合环路径,为了方便操作,只需在合环模式2的仿真模型下调换各负荷即可,对比结果如表3所示。

表3 合环模式2各负荷合环参数对比
从表3可以看出,S左2和 S左3与 S右/2之间的电压差和相角差较小,均能完成合环操作。S左2对合环线路的冲击更小,是运行人员选择的最佳线路。因此合环操作时应避免合环两端负荷相差较大的情况,尽量选择两端负荷相近的线路进行合环。同时如若在负荷低谷时进行合环操作,也能提高合环操作成功率。
5 结语
本文基于叠加定理和戴维南定理推导了配电网合环稳态电流和冲击电流的数学模型,对配网三种合环模式及其不同馈线下的合环电流建立了合理的仿真模型,通过PSCAD软件验证了合环电流与合环点电压差、总阻抗的关系,得到了合环稳态电流和冲击电流的近似结果,找到了最佳合环路径,最后利用仿真结果总结了合环操作的通用结论,为电网现场运维人员提供了较为合理的理论指导,为配电网能够更加安全稳定运行提供了操作依据。
