两参数随机过程的一致随机连续性*
2019-05-05刘丹华杨婵娟
刘丹华,杨婵娟
(湘潭大学数学与计算科学学院,湖南 湘潭 411105)
多参数随机过程由单参数随机过程演变而来,但却与单参数随机过程有本质区别.两参数随机过程是一类重要的多参数随机过程,如Poisson单、Levy单和两参数马尔可夫过程等.文献[1-2]对两参数随机过程及其一致随机连续性进行了分析,笔者拟研究一致随机连续性与矩形增量的关系,建立两者之间的联系.
1 符号说明


2 主要结果
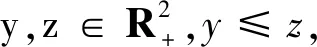
X(y,z]=X(z)-X(y⊗z)-X(z⊗y)+X(y).
矩形增量也可记为
X(y,z]=Xs,t-Xu,t-Xs,v+Xu,v.
(1)


根据极限的定义,可得如下等价定义:

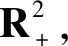
显然,如果X在区域D上一致随机连续,那么X在区域D上必定随机连续.根据连续函数的康托定理[3],可以类似地证明:如果X在有界闭区域D上随机连续,那么X在有界闭区域D上必定一致随机连续.
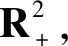
定理1曾在文献[1,P190]中直接引用.
定理2设Y={Ys,t,(s,t)∈R2+},称Y为定义在概率空间(Ω,F,P)以(R,B(R))为状态空间的零初值的两参数随机过程.设有界区域D=[(0,0),(M,M)],0
区域D=[(0,0),(M,M)],0
注1有界区域D不一定要求是有界的正方形.事实上,只要求有界区域D满足条件:如果点(s,t)∈D,那么长方形[(0,0),(s,t)]⊂D.实际上,这样的有界区域是平面上第一象限里由坐标轴构成的一个曲边直角三角形,斜边是一条单调不增的连续曲线(图1).
3 定理证明
定理1的证明因X在区域D上一致随机连续,故对于∀ε>0,η>0,存在δ0=δ0(ε,η)>0,对于∀(u,v),(s,t)∈D,当|u-s|<δ0,|v-t|<δ0时,
(2)


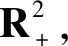
证毕.
定理2的证明充分性已在定理1中证明,接下来证明必要性.任取2点y,z∈D,y=(u,v),z=(s,t),y≤z.设区域A1=((0,v),(u,t)],区域A2=(y,z],区域A3=((u,0),(s,v)],则由(1)式和定义2可得
Y(A1)=Yu,t-Yu,v,Y(A2)=Ys,t-Yu,t-Ys,v+Yu,v,Y(A3)=Ys,v-Yu,v,
于是Ys,t-Yu,v=Y(A1)+Y(A2)+Y(A3).
再由已知条件可知,对于∀ε>0,η>0,存在δ1=δ1(ε,η)>0,对于长方形A1=((0,v),(u,t)]⊂D,当|A1|=u(t-v)<δ1时,
(8)
同理可得:对于ε>0,η>0,存在δ2=δ2(ε,η)>0,对于长方形A2=(y,z]⊂D,当|A2|=(s-u)×(t-v)<δ2时,
(4)
对于ε>0,η>0,存在δ3=δ3(ε,η)>0,对于长方形A3=((u,0),(s,v)]⊂D,当|A3|=(s-u)v<δ3时,
(5)

|A1|=u(t-v)≤M(t-v) |A3|=(s-u)v≤M(s-u) . 于是由(3)—(5)式,可得 证毕.
