基于自然边界元的一类拟线性问题的数值算法*
2019-05-05高志宇姚雪春
高志宇,姚雪春
(南京财经大学应用数学学院,南京 仙林 210046)
在物理学、工程技术学等诸多领域中,大部分的计算问题可以归结为区域上的偏微分方程数值问题,边界元法和有限元法等数值方法被广泛应用.但自然边界元法在单独处理非线性问题上困难重重,而有限元法能适应较任意的区域及更广泛的问题;因此,针对某些特殊的非线性问题,就产生了自然边界元与有限元耦合法[1-3].
1 非重叠型区域分解算法
根据边界的具体特点,笔者以椭圆弧作为人工边界,利用非重叠型区域分解算法(即Dirichlet-Neumann(D-N)交替算法)研究长条形区域上的拟线性方程[4-6].设Ω为R2上具有长条形内边界的简单有界连通区域,且有足够光滑的边Γ,则

(1)
在静磁学领域,a表示磁导率,u表示标量磁势;在流体力学领域,a表示密度,u表示标量速度势.

图1 椭圆人工边界Fig. 1 Elliptic Artificial Boundary
对于问题(1),选取椭圆人工边界(图1),即以原点为中心,作椭圆弧Γ1={(μ,φ)|μ=μ1,0≤φ≤2π},满足dist(Γ,Γ1)>0.这样,Γ1将区域Ω分成Ω1和Ω22个子区域,其中Ω1是Γ1,Γ围成的有界区域,Ω2是Γ1以外的无界区域.
由文献[5,7]可知,a(x,u)和Γ1满足:
(1)函数f的紧支集suppf⊂Ω1;
(2)对于∀u∈R,存在常数C0,C1∈R,使得
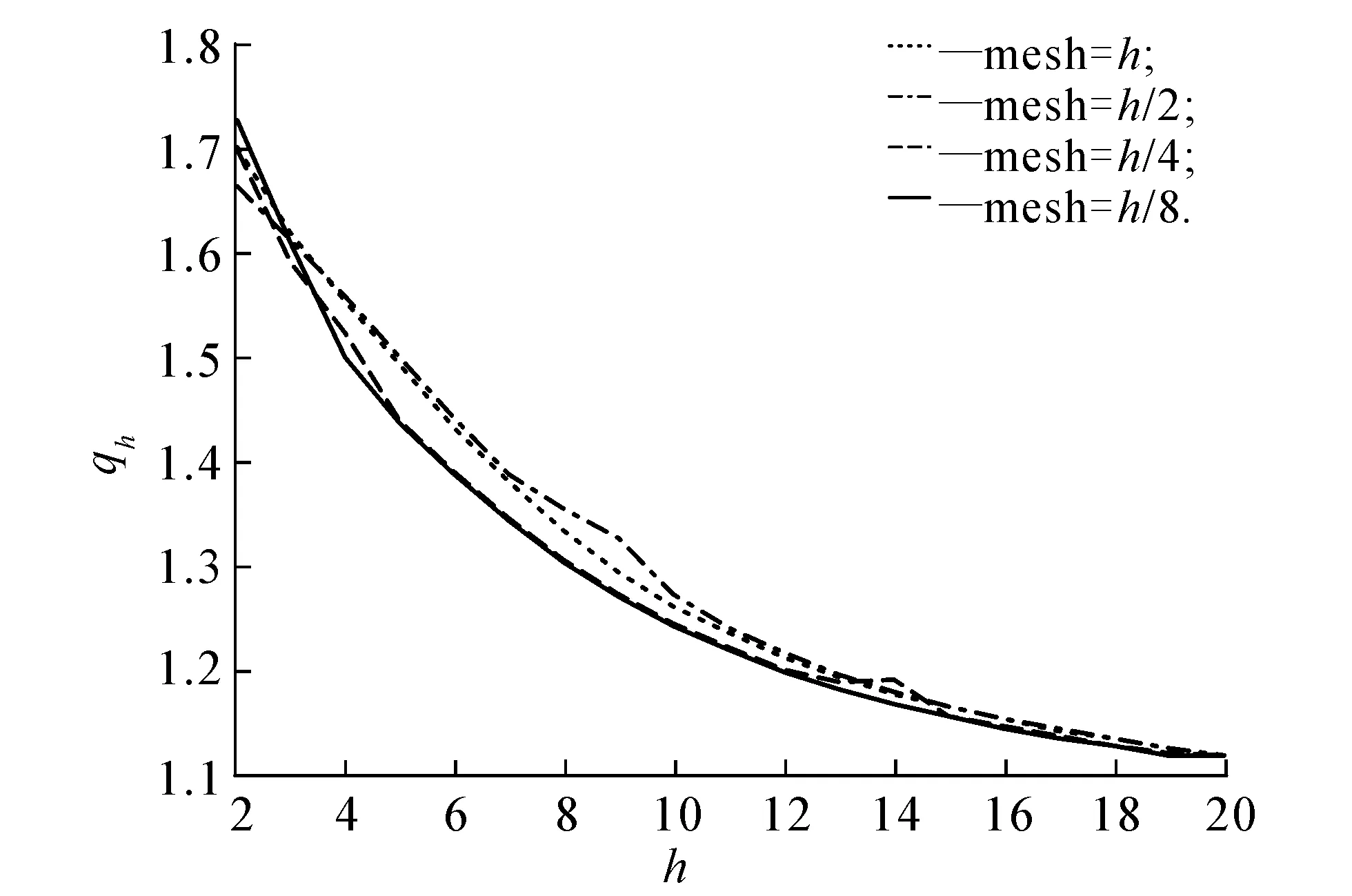
0 (2) (3)对于∀u,v∈R和几乎所有的x∈Ω,存在常数CL>0,使得 |a(x,u)-a(x,v)|≤CL|u-v|. D-N交替算法的步骤如下: (ⅱ)在Ω2上求解边值问题 (3) (ⅲ)在Ω1上求解混合边值问题 (4) (ⅴ)令k=k+1,转(ⅱ). 在上述步骤中,松弛因子δk可取适当的实数,问题(3)可用自然边界元法求解,问题(4)可用有限元法求解.此外,因为只需求问题(3)的解在Γ1上的法向导数值,所以无须直接求解问题(3).基于Kirchhoff变换,利用自然边界元法可得问题(3)的自然积分方程. 对于区域Ω2上的边值问题,由Kirchhoff变换[8]可得 (5) 由自然边界归化原理,得到Possion积分公式 (6) 相应的自然积分方程为 (7) (6)和(7)式的傅里叶形式分别为 (8) 由(5)式可得 (9) 由(8)和(9)式可得Γ1上的精确的边界条件 对于问题(4),引入标准Sobolev空间Wm,p,‖·‖和|·|分别参照范数和半范数的定义,给出新定义: Hm(Ω)=Wm,2(Ω),|·|m,Ω=|·|m,2,Ω,‖·‖m,Ω=‖·‖m,2,Ω. 其解空间V={v∈H1(Ω1)|v|Γ=0},相应范数为 边值问题(6)等价于如下变分问题:求u∈V,使得 a(u;u,v)+b(u;u,v)=F(v) ∀v∈V. (10) 其中: Vh={vh∈V|v|K是一个线性多项式,∀K∈ζh}, 则近似问题(10)可以转化为:求uh∈V,使得 a(uh;uh,vh)+b(uh;uh,vh)=F(vh) ∀vh∈Vh. (11) 其中: 引理1存在常数C2>0,使得 |a(u;u,v)+b(u;u,v)|≤C2‖u‖1,Ω1·‖v‖1,Ω1, 根据离散化问题(11),与线性问题的研究结果类似,可得如下形式的线性方程组: (12) 方程组(12)可以转化为 于是有迭代算法 (13) Λk+1=δkUk+(1-δk)Λkk=0,1,2…. (14) 定理 2当0 现给出一个数值实例,以说明D-N交替算法的可行性.对于拟线性问题 图2 8×32三角形网格剖分Fig. 2 Mesh of Triangle Subdivision is 8×32 图3 网格参数h与收敛速度qh的关系Fig. 3 Relationship Between Mesh Parameters h and Convergence Rate qh 网格收敛速度k012345he(k)0.151 6580.118 2690.098 6660.086 5760.078 8070.073 604eh(k)0.033 3890.019 6030.012 0900.007 7690.005 203qh(k)1.703 1981.621 5141.556 1061.493 124 表1(续)Table 1 (continued) 由以上结果可以看出,D-N交替算法是收敛的,且随着迭代次数的增加,收敛速度与网格参数h无关. 利用D-N交替算法和自然边界元与有限元耦合法研究了长条形区域上的拟线性问题.根据区域形状特点,引入椭圆弧人工边界,用D-N交替算法解决了一类特殊的非线性算子拟线性问题,并给出迭代的收敛性分析.数值实例的结果表明,D-N交替算法对拟线性问题是可行且有效的.
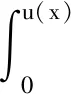


2 等价变分问题

3 有限元逼近



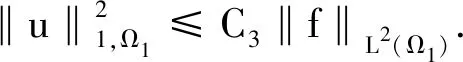
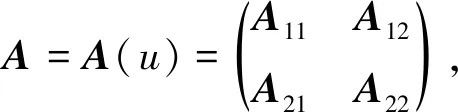


4 数值实例

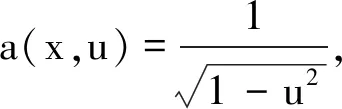



5 结语
