具有较少非中心共轭类数的有限群*
2019-05-05栾书静何立国
栾书静,余 航,何立国
(沈阳工业大学理学院数学系,辽宁 沈阳 110870)
设G是非交换有限群,bcl(G)是群G的最大共轭类长,S(G)是群G的基柱,即G的所有极小正规子群的积.群G的非中心共轭类对群G的结构有重要影响[1-4].李美艳等[5]、温海风等[6]给出了群G的非中心共轭类数至多为5时群G的结构,VERA-LOPEZ A等[7-9]刻画了共轭类数不超过14时群G的结构.以此为基础,笔者拟给出非中心共轭类数介于6与9之间时群G的结构,以及非中心共轭类数是10且有可解基柱时群G的结构.文中的符号及术语除特别说明之外,与文献[7-8]一致.


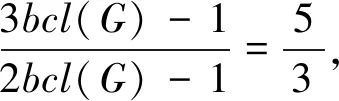
证毕.

证明由不等式2zbcl(G)≤|G|≤z+nbcl(G)即可得.
定理1设n是群G的非中心共轭类数,若6≤n≤9,则G同构于下列群之一:
(1)当n=6,s≤12时,G≅C13×fC3,D22,C7×fC6,C13×fC4,C11×fC5,S5,A6,C2×D10,C5×λC4,C2×A4,GL(2,3),SL(2,3)·C4,C3×λS3,C2×D8,C4×λC4,(C4×C2)×λ1C2或C8×λC2.
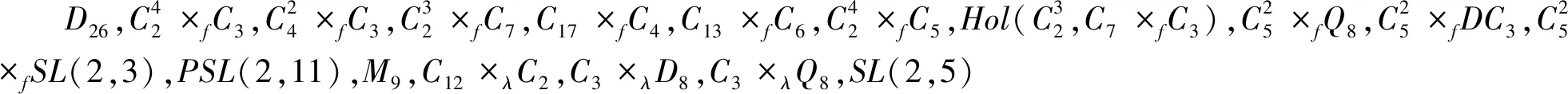

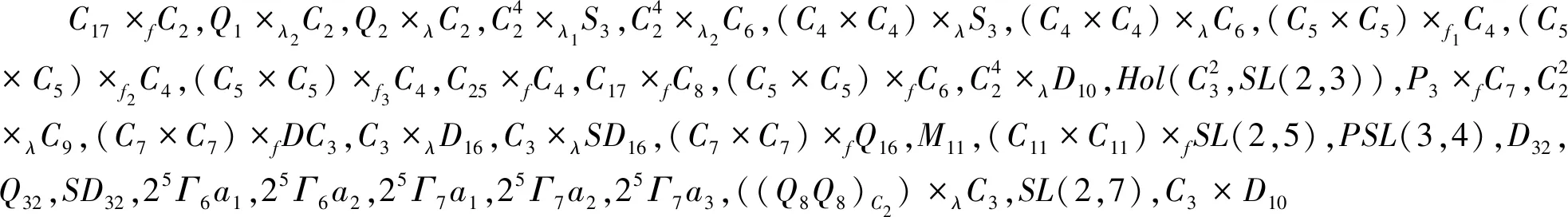
(5)当6≤n≤9,13≤s≤14时,非幂零群G包含在文献[9]的表1或表3中,幂零群G是27阶群或阶最大为128的2-群.
(6)当n=9,s=15时,G≅C3×D8或C3×Q8.
证明若n≤9,由引理1得s≤15,若s=15,由引理1得n≥9,因此n=9,z=6.由不等式2zbcl(G)≤|G|≤z+nbcl(G),可得bcl(G)=2,|G|=24.根据文献[7-9]可得s≤14的有限群结构,而通过GAP计算可知z=6,n=9,24阶群中仅有群C3×D8或C3×Q8满足条件s=15.
证毕.
定理2设n是群G的非中心共轭类数,群G的基柱S(G)是可解的,若n=10,则G同构于下列群之一:
(1)当bcl(G)=2时,G=P×A,P是G的Sylow-2子群,A是交换群.
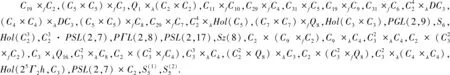
(3)当13≤s≤14时,非幂零群G包含在文献[9]的表1或表3中,幂零群G是2-群且阶最大为128.
(4)当s=15时,G≅C5×S3.

证毕.
