Mlinex损失函数下的信度递归模型*
2019-05-05毕锋霄
赵 珍,毕锋霄
(1.新疆财经大学统计与信息学院,新疆 乌鲁木齐 830012;2.69236部队,新疆 沙湾 832100)
1 问题的提出

然而,在经典的信度理论中得到的保费是纯保费,这容易导致保险公司破产.解决该问题的一种方法是修改损失函数.C K Podder等[6]提出了一类修正的线性指数损失函数,即
其中θ为未知参数,δ为θ的估计,该函数称为Mlinex损失函数.当c>0时,Mlinex损失函数可以很好地刻画负偏差引起的损失低于正偏差引起的损失.近年来,该损失函数在理论和应用方面得到广泛研究[7-10].由于这种预测方法得到的保费是建立在历史索赔额权重相同的基础上,并没有考虑年份远近的影响,因此V Atanasiv[11]提出了一种更合理的方法,即将年份较近的索赔额赋予较大的权重,年份较远的索赔额赋予较小的权重,从而得到递归信度模型.笔者拟在文献[11]的基础上,考虑以Mlinex损失函数作为估计误差的度量,推导出相应的保费递归公式.
2 模型准备
假设某个保单前t年的索赔额为Y1,Y2,…,Yt,由风险参数Θ识别,Θ=(θ1,θ2,…,θt),Θ是不可测随机变量,先验分布为π(Θ),给定θj,Y1,Y2,…,Yt是相互独立的.
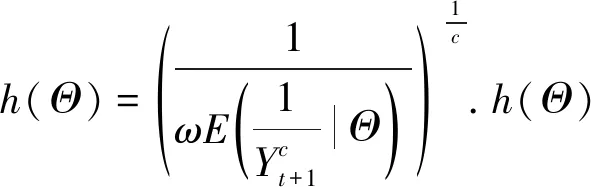

(1)

性质1和性质2的证明可参考文献[12].
3 信度递归模型
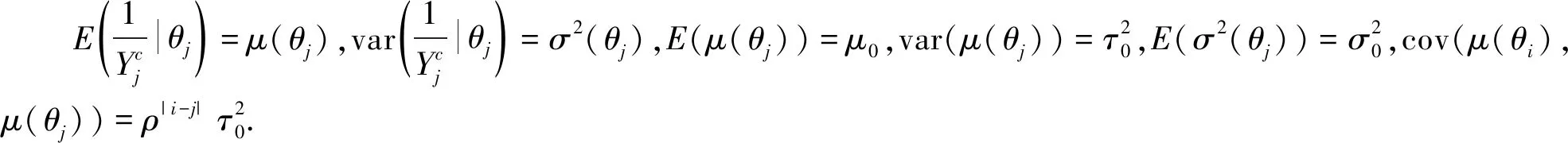
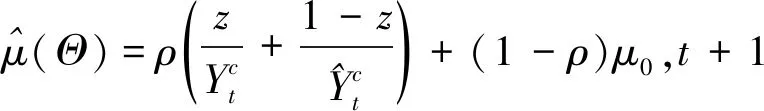
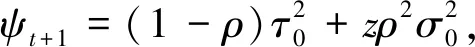



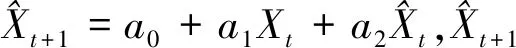
(2)
(3)
由(2)和(3)式,得到
(4)
从而a1+a2=ρ.
令a1=ρ-a2,代入(4)式,并令j=t,可得
(5)
又
(6)
(7)
因为
(8)

从而μ(Θ)的信度估计
风险保费h(Y|Θ)的信度估计
而
其中:
cov(μ(θt+1),Xt)=E(E(μ(θt+1)Xt|θt))-E(μ(θt+1))E(E(Xt|θt))=
E(μ(θt+1)E(Xt|θt))-E(μ(θt+1))E(μ(θt))=
于是
证毕.
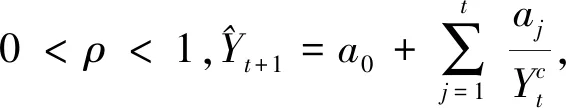
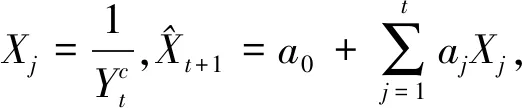
对于∀j=1,2,…,t-1,令

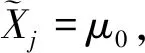
于是
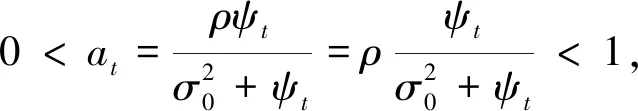
证毕.
4 结语