一种无人机低仰角测控通信信道建模方法研究

李海鹏，吕 瑶

(中国人民解放军92941部队，辽宁 葫芦岛 125000)

0 引言

当无人机处于低仰角飞行模式时，其信道条件较为复杂，一般而言是直射、反射与散射分量的排列组合，只有准确地对信道进行建模才能正确地选择传输体制以及抗多径传输技术。由于受到收发天线波束宽度、无人机外形以及地面测控站周围环境的影响，无人机测控通信信道中的散射分量与移动通信有较大区别。文献[1-5]均将散射分量建模成入射角在一定范围内分布的随机变量，没有讨论信道的时变特性。而实际上这种时变性对导频以及循环前缀CP长度的选择具有较大影响。本文在分析无人机低仰角测控通信信道特性的基础上，采用正弦波叠加法[6]给出了一种建模方法，并对散射分量的时变性进行了讨论与仿真验证。

1 无人机低仰角测控通信信道模型

1.1 信道特点

低仰角条件下的无人机测控通信信道一般包含直射、反射与散射分量，其信道特性呈现出卫星通信与移动通信信道相结合的特点[7]，如图1所示。视距条件下，无人机空地信道存在直射径，平滑的大地或水面会形成信号的镜面反射从而引入反射分量[8]，而测控站周围的大型建筑物或山体会引起信号的多径传播，导致信号衰落，称为散射分量。

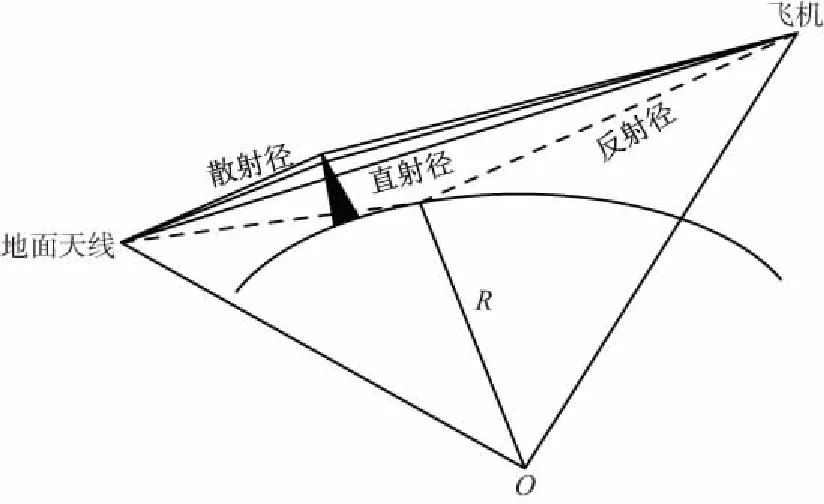
图1 无人机低仰角信道中直射、反射与散射分量示意

1.2 信道数学模型

无人机空地通信信道的统计特性与飞行状态、载波频率、信号带宽和收发天线方向图等因素有关。飞行状态一般包括停机、滑行、起飞、平飞和降落等状态，不同飞行状态对应的飞行速度与周围环境各异，相应的多普勒与时延扩展也不相同。无人机使用的载波频率涵盖范围较广(包括VUHF，L，S，C，X等频段)，载波频率决定了信号空间大尺度路径衰减值、波束宽度和载波多普勒等参数取值。无人机信号既有低速的遥控遥测数据，也有高速的载荷数据，不同信道带宽决定了频率选择性衰落大小[9]。收发天线方向图主瓣越窄，多径分量的抑制度越高。因此，无人机信道统计特性建模是一个受多参数影响的复杂过程，停机、滑行状态下无人机信道可采用移动通信地—地信道模型进行建模，起飞、降落阶段仰角较高，信道条件较为良好。本文主要关注远场低仰角条件下无人机信道建模问题。

在远距离低仰角条件下，空—地信道中存在反射径，其相对于主径的延迟可以利用移动通信系统中大尺度地面反射双径模型进行分析。此时无人机信道可以表示为：

hLOS_R(t，τ)=αLOSexp(j2πfLOSt)δ(τ)+

αRexp(j2πfRt)exp(jθ0)δ(τ-τ0)，

(1)

式中，αLOS表示直射径上信号幅度；αR，fR分别表示地面反射路径上的传输信号幅度与载波多普勒频率；τ0表示反射路径上的信号相对直射径的时间延迟；θ0表示地面反射波的随机相位。

当无人机机载与地面终端均采用定向天线通信时，天线波束较窄，发生散射时塔台或飞机接收到平面波的入射角分布范围也较窄[10-11]。此时由于波束的选择性导致多条发射径中入射角被限制在一定范围内，地面或海面引入的反射径较小，在这种情况下需要对其衰落性重新分析与建模，远场低仰角无人机信道一般用有直射与散射径的双径莱斯信道表征[12]。含有直射与一簇散射径的双径莱斯信道可以表示为：

hLOS_fading(t，τ)=αLOSexp(j2πfLOSt)δ(τ)+

(2)

式中，N表示散射路径数；αn，fn，θn，τn分别表示第n条散射径上的信号幅度、载波多普勒频率、随机相位和相对于直射径的时间延迟[13]。通过极限求和得到多径散射情况下的散射分量hfading，无人机处于低仰角条件下，发生多径散射时入射角分布示意图如图2所示。其中，fD表示散射径最大多普勒频移，[θL，θH]表示散射径入射范围。

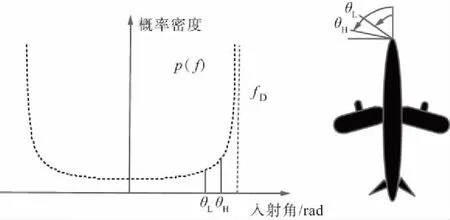
图2 无人机信道散射分量入射角分布

工程应用中，在较窄的散射径入射范围[θL，θH]内，散射分量hfading可近似表示为：

(3)

式中，Φn(t)表示取值在[0，2π]上的随机相位。在给定的时刻t，x(t)与y(t)为多个独立、零均值随机变量之和。根据中心极限定理，x(t)与y(t)可被视为2个零均值的高斯随机变量，并且方差都等于散射径的功率Pd。散射径多普勒频偏f=fDcosθ，θ表示地面站接收散射信号的入射角。由于θ在[θL，θH]上服从均匀分布，所以对概率密度p(f)而言，当fDcosθH≤f≤fDcosθL或者fDcosθL≤f≤fDcosθH时，取非零值，

(4)

这样就可得到hfading(t)的功率谱密度为：

(5)

经过推导可知，hfading(t)的自相关函数为:

E(hfading(t)hfading(t+τ))=E(x(t)x(t+τ))cos(2πfCτ)+

E(x(t)y(t+τ))sin(2πfCτ)，

(6)

现定义hfading(t)同相与正交分量的自相关与互相关函数g(τ)和h(τ)分别为：

g(τ)=E(x(t)x(t+τ))=

(7)

h(τ)=E(x(t)y(t+τ))=

(8)

g(τ)和h(τ)无闭合表达式，只能通过计算仿真给出数值解。

2 实验仿真

2.1 无人机低仰角测控通信信道仿真模型

当信号速率较高时，无人机低仰角信道可建模为包含直射与散射径的双径莱斯信道。定义莱斯因子K=Ps/Pd。信道仿真模型如图3所示。其中，直射径可以建模为一个受功率因子与直射径载波多普勒频率影响的乘性信道[14]。而在任意角度区间上分布的散射径可以采用正弦波叠加法进行建模，针对hfading(t)表达式，各参数定义为：

(9)

(10)

fn=fDcosθL+nΔf或fDcosθH+nΔf。

(11)

各个正弦波上的角度取随机值。由于受到散射体的影响，fD与载波多普勒频偏并不相同。

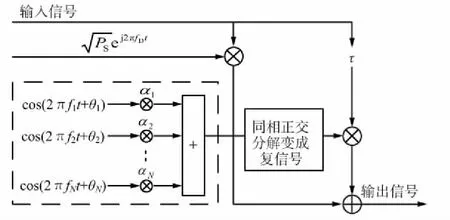
图3 双径莱斯信道仿真模型

2.2 仿真结果

散射信道中入射角在[π/6，π/4]和[0，2π]区间内均匀分布时相关函数的理论曲线如图4所示。当入射角在[0，2π]区间内均匀分布时，散射信道为Rayleigh信道，其互相关值为0，自相关值呈0阶贝塞尔函数形状；而当入射角在[π/6，π/4]区间内均匀分布时，其互相关值并不为0，这就表明I、Q两路信号有较强的相关性，而自相关函数在较大的时间间隔上依然会保持很强的相关性[15]。

图4 散射信道中不同入射角度时信道时域相关曲线

散射信道中不同入射角对应的时域包络衰落示意图如图5所示。从图中可以看出，当入射角在较小范围时，信道时变速率要明显慢于[0，2π]上均匀分布的情况。这是由于前者I、Q两路信号有较强的相关性，2路衰落系数不再独立，导致其时域衰落速率较慢。这一点与移动通信系统的Rayleigh衰落信道有明显区别。

图5 散射信道中不同入射角度时信道时域包络幅度曲线

采用2.1节介绍的双径莱斯信道模型设计的2个不同信道的BER特性曲线如图6所示。仿真条件为：系统采用SC-FDE传输体制、BPSK调制，信息速率为2 Mb/s，双径信道时延为[0，1.5 μs]，直射径的载波多普勒频率为5 kHz(包括无人机运动引起的载波多普勒频率和机地本振频偏。其中载波多普勒频率较小，主要取决于本振频偏)，散射径的最大多普勒频移为100 Hz(fC=450 MHz、无人机速度v=67 m/s，对应载波多普勒为100 Hz)，称莱斯因子为9 dB和6 dB的信道分别为信道A和B。通过对比可以看出，莱斯因子对系统性能有较大的影响[16]。与K=9 dB的信道A相比，K=6 dB的信道B的BER特性恶化较为明显。这就要求无人机或测控站天线主波瓣较窄，具有较强的抑制多径的能力[17]。

图6 不同莱斯因子信道下系统的BER曲线

3 结束语

针对无人机低仰角测控通信信道建模问题，在分析信道特性的基础上给出了一种双径莱斯信道[18]建模方法。利用该建模方法不仅可以便捷地设置直射径功率因子与载波多普勒频偏，还可以设置不同入射角范围、散射径多普勒频偏和功率因子等参数条件下的散射时变信道，对工程中设计无人机信道模拟器具有一定的参考价值。